Outline Introduction Shortest Route Problems Formulation Labeling Algorithm

Outline èIntroduction èShortest Route Problems èFormulation èLabeling Algorithm 1

Chapter 8 Network Optimization Model & PERT/CPM 2

Structure of Chapter 8 è 8. 1 Network Models 網路模型 è 8. 1. 1 The Shortest Route Problem 最短路徑問題 è 8. 1. 2 The Minimum Spanning Tree Problem 最小 延展樹問題 è 8. 1. 3 The Maximal Flow Problem 最大流量問題 è 8. 2 PERT / CPM 計劃評核術/要徑法 3

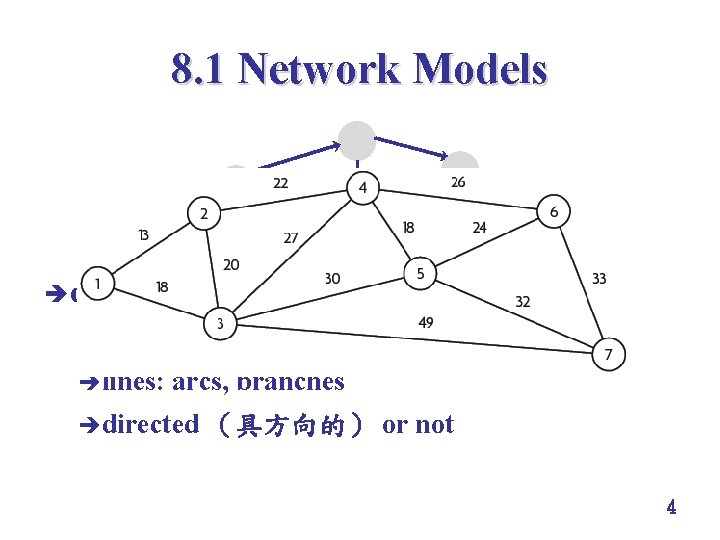
8. 1 Network Models 2 4 1 3 è definitions ècircles: èlines: nodes (節點), vertices (角) arcs, branches èdirected （具方向的） or not 4

Formulation of the Shortest Route Problem 5

8. 1. 1 The Shortest Route Problem 最短路徑問題 è motivation: to find the shortest route from the origin (起點， i. e. , one location, source node) to the destination (終點， i. e. , another location, sink node) in a network è driving, è what production and inventory problems, etc. to do? è formulation, with known parameter values aij, sj i j aijxij, è solution methods s. t. an optimizer, a solver optimal solution i xij - i xji = sj for all j 6

Formulation è the formulation for the shortest distance between node 1 and node 6: è Min z = 5(x 12+x 21)+8(x 13+x 31)+7(x 14+x 41)+6(x 23+x 32)+1(x 34+x 43)+13(x 25+x 52) +7(x 35+x 53)+16(x 46+x 64)+6(x 56+x 65) s. t. (i. e. , subject to): x 12+x 13+x 14 = 1 (source node) x 12+x 32+x 52 = x 21+x 23+x 25 (node 2) x 13+x 23+x 43+x 53 = x 31+x 32+x 34+x 35 (node 3) x 14+x 34+x 64 = x 41+x 43+x 46 (node 4) x 25+x 35+x 65 = x 52+x 53+x 56 (node 5) x 56+x 46 = 1 (node 6) xij = 0 or 1 for all i, j combinations How to formulate? 只要細想，每個人都懂。 要是不知如何下手，就 從簡單的問題開始。 7

Formulation (建模) è a one-arc, two-node problem è source node 1 è sink node 2 9 1 2 7 how to formulate? è either the upper or the lower route （上路還是下路？ ） ; how to model mathematically? è min 9 U + 7 L 數學模式(formulation)只是用精 s. t. 練（複雜？）的語言表達日常的 U+L=1 事物，所以建模的重點在補捉事 U, L {0, 1} 物的要素、精髓。如上述問題， 什麼是最重要的決定？ è 8

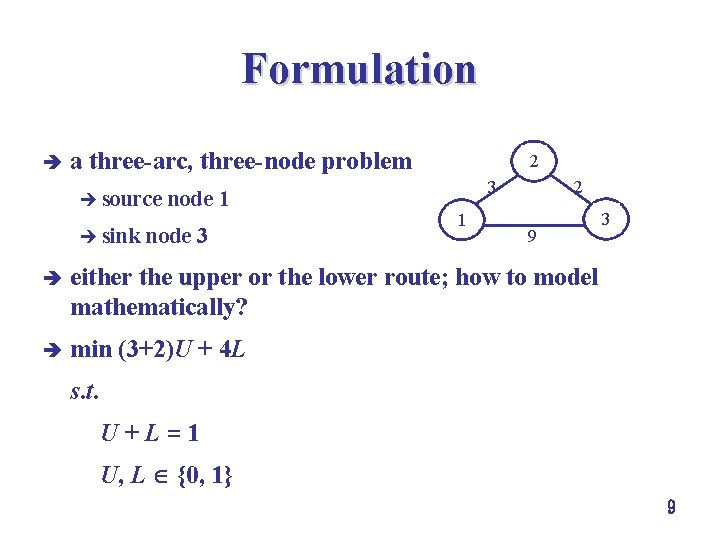
Formulation è a three-arc, three-node problem è source è sink node 1 node 3 2 3 1 2 9 è either the upper or the lower route; how to model mathematically? è min (3+2)U + 4 L 3 s. t. U+L=1 U, L {0, 1} 9

Formulation è Of course we know the shortest distance between node 1 and node 4. 2 我們當然曉得在最短的路徑中我 們會從node 2跑去node 3，但在 formulation中我們不能直接引用 最短路徑的結果。 3 5 2 1 6 3 4 1 What is the direction of flow in the middle arc, upward or downward? Or any flow at all? è However, in a formulation we better do not assume any knowledge about the optimal solution. è How to formulate? 10

Formulation èIn our context, formulation is the process to express the dynamics a physical phenomenon mathematically in terms of variables that we define. physical phenomenon formulation, with known parameter values aij, sj i j aijxij, s. t. i xij - i xji = sj for all j 建模是邏輯問題，不是數學問題。每一條限制式都代表系統中一種實 在的現象。要建模就得先掌握這些實在的現象，才能用變量表達。 11

Formulation è properties of a route from the source to the sink: èeach route represented by a collection of xij = 1, with the other off-route variables = 0 èsource: èsink: 2 one arc out one arc in èintermediate 3 6 6 3 4 2 1 6 1 5 3 4 1 2 5 2 1 3 3 node: one arc in and one arc out 2 3 5 2 1 2 3 4 1 5 2 1 6 3 4 1 12

Formulation 2 3 2 1 6 è min 5 3 x 12 + 6 x 13 + 2(x 23+x 32) + 5 x 24 + x 34, 3 4 1 s. t. x 12 + x 13 = 1 (node 1, source) x 12 + x 32 = x 23 + x 24 (node 2) x 13 + x 23 = x 32 + x 34 (node 3) x 24 + x 34 = 1 (node 4, sink) x 12, x 13, x 32, x 24, x 34 {0, 1} 選最node 1到node 4最短徑，就像將一單位 （1 unit）的水從node 1送到node 4，水流 過的arcs就是在路徑上的arcs. 13

Formulation - Question è min 3 x 12 + 6 x 13 + 2(x 23+x 32) + 5 x 24 + x 34, s. t. x 12 + x 13 = 1 (node 1, source) 3 x 12 + x 32 = x 23 + x 24 (node 2) 1 x 13 + x 23 = x 32 + x 34 (node 3) 6 x 24 + x 34 = 1 (node 4, sink) x 12, x 13, x 32, x 24, x 34 {0, 1} both x 23 and x 32 be positive at minimum? 2 5 2 3 4 1 è Would 14

Formulation è 3 tricks in our formulation only outflow from source node è only inflow to destination node è è 2 5 2 1 6 3 4 1 variables x 21, x 31, x 42, and x 43 set to zero in the textbook è min 3(x 12+x 21) + 6(x 13+x 31) + 2(x 23+x 32) + 5(x 24+x 42) + (x 34+x 43), s. t. x 12 + x 13 = 1 (node 1, sosurce) x 12 + x 32 + x 42 = x 21 + x 23+x 24 (node 2) x 13 + x 23 + x 43 = x 31 + x 32 + x 34 (node 3) x 24 + x 34 = 1 (node 4, destination) x 12, x 13, x 32, x 24, x 34 {0, 1}; x 21 = x 31 = x 42 = x 43 = 0 15

Formulation - Question è Would the following formulation be all right? è min 3(x 12+x 21) + 6(x 13+x 31) + 2(x 23+x 32) + 5(x 24+x 42) + (x 34+x 43), s. t. x 12 + x 13 = 1 (node 1, sosurce) x 12 + x 32 + x 42 = x 21 + x 23+x 24 (node 2) x 13 + x 23 + x 43 = x 31 + x 32 + x 34 (node 3) x 24 + x 34 = 1 (node 4, destination) 2 3 5 2 1 6 3 4 1 x 12, x 13, x 32, x 24, x 34 , x 21, x 31, x 42, x 43 {0, 1} è Example 8. 2 of the textbook uses the above formulation. 16

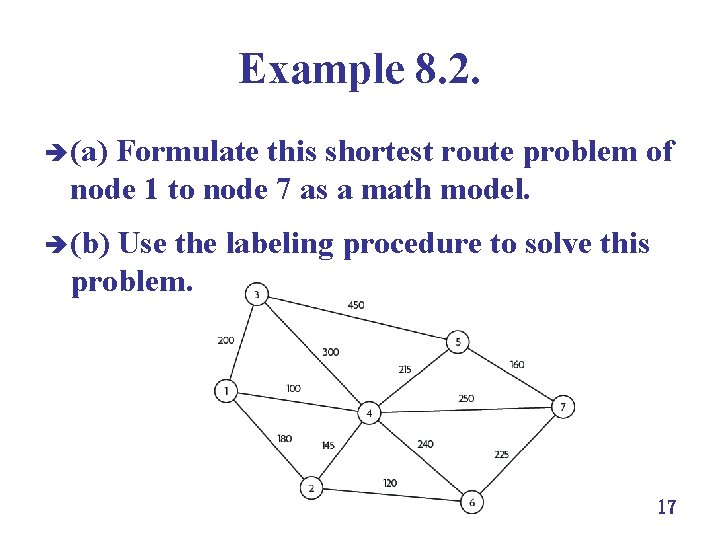
Example 8. 2. è (a) Formulate this shortest route problem of node 1 to node 7 as a math model. è (b) Use the labeling procedure to solve this problem. 17

Formulation è the formulation for the shortest distance between node 1 and node 6: è Min z = 5(x 12+x 21)+8(x 13+x 31)+7(x 14+x 41)+6(x 23+x 32)+1(x 34+x 43)+13(x 25+x 52) +7(x 35+x 53)+16(x 46+x 64)+6(x 56+x 65) s. t. (i. e. , subject to): x 12+x 13+x 14 = 1 (source node) x 12+x 32+x 52 = x 21+x 23+x 25 (node 2) x 13+x 23+x 43+x 53 = x 31+x 32+x 34+x 35 (node 3) x 14+x 34+x 64 = x 41+x 43+x 46 (node 4) x 25+x 35+x 65 = x 52+x 53+x 56 (node 5) x 56+x 46 = 1 (node 6) xij = 0 or 1 for all i, j combinations Actually it is possible to drop the red variables. 18

Algorithms for the Shortest Route Problem 19

Algorithms Background è how to determine the shortest route? è background: development of computers èmade possible computation for large networks èled to step by step instructions to teach a computer to calculate 20

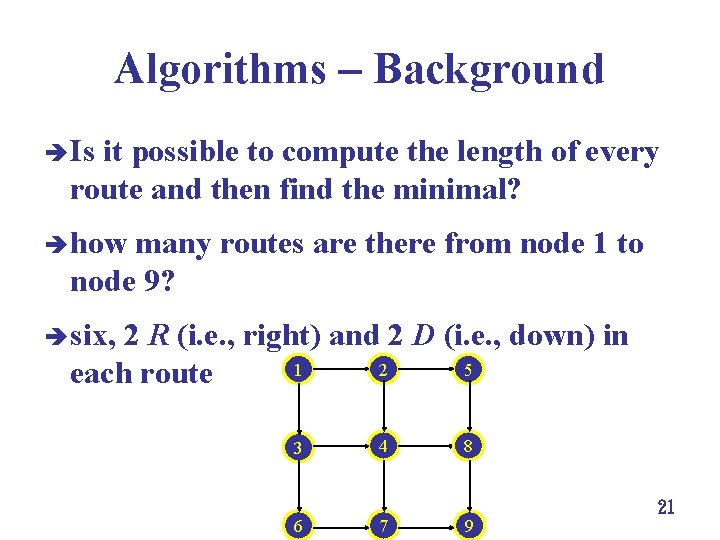
Algorithms Background è Is it possible to compute the length of every route and then find the minimal? è how many routes are there from node 1 to node 9? è six, 2 R (i. e. , right) and 2 D (i. e. , down) in 1 2 5 each route 3 6 4 7 8 9 21

Algorithms Background è the total number of routes increases quickly with number of nodes. è what is a quicker method? 在一個N 2節點的網路 中，路徑的總數目 是(2 N!)/(N!N!) # of nodes 9 25 121 441 961 # of routes 6 70 252 5. 41 1011 467 1017 22

The Labeling Algorithm for the Shortest Route Problem 23

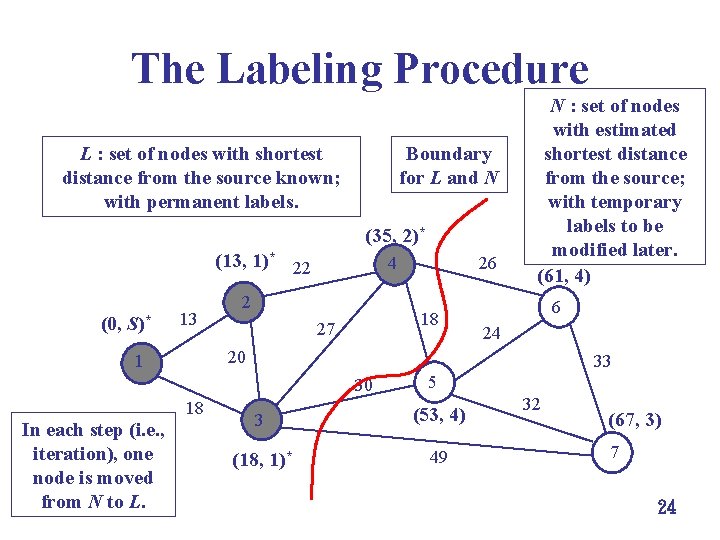
The Labeling Procedure L : set of nodes with shortest distance from the source known; with permanent labels. Boundary for L and N (35, 2)* (13, 1)* 22 (0, S)* 13 4 2 18 27 6 24 20 1 33 30 In each step (i. e. , iteration), one node is moved from N to L. 26 N : set of nodes with estimated shortest distance from the source; with temporary labels to be modified later. (61, 4) 18 5 3 (53, 4) (18, 1)* 49 32 (67, 3) 7 24

The Labeling Procedure èa simple procedure in which the effort grows slowly with the number of nodes （運算所需的功 夫隨節點的數目慢慢增加） è notions defined for the execution of the labeling procedure è two sets of nodes, L (nodes with well-defined distance from source node S) and N (nodes with temporary, estimated distance from source S) label （永久標籤） (d, y)* of a node x L: the shortest route from S to x is of d units, and it passes through y before going into x è permanent 25

The Labeling Procedure è two sets of nodes, L and N, during execution of the procedure è L, set of labeled nodes è nodes with definite distance from source S è before è after è N, executing the algorithm: L = {S} executing the algorithm: L = the set of all nodes set of non-labeled nodes è nodes with temporary, estimated distance from source S è before è after executing the algorithm: N = all nodes except S executing the algorithm: N = 26

Idea of the Labeling Procedure è three-node network, node 1 as source and node 3 as destination è what is the shortest distance from node 1 to node 3? è we need an executable procedure for a computer 2 3 1 2 9 3 27

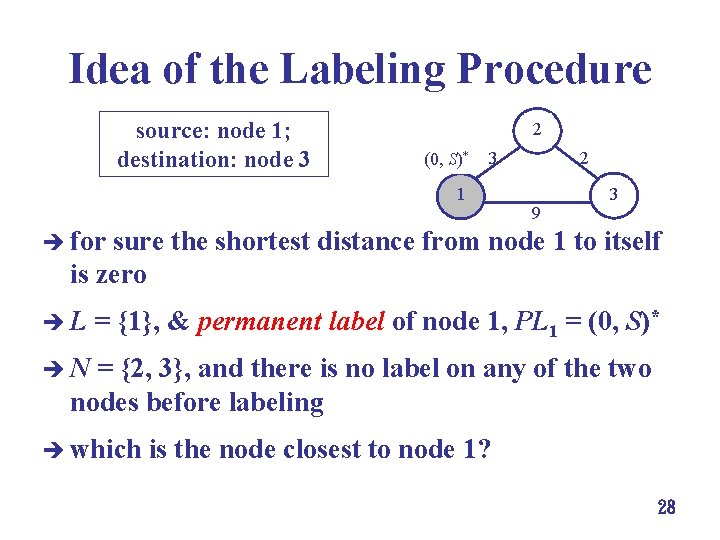
Idea of the Labeling Procedure source: node 1; destination: node 3 2 (0, S)* 3 1 2 9 3 è for sure the shortest distance from node 1 to itself is zero èL = {1}, & permanent label of node 1, PL 1 = (0, S)* èN = {2, 3}, and there is no label on any of the two nodes before labeling è which is the node closest to node 1? 28

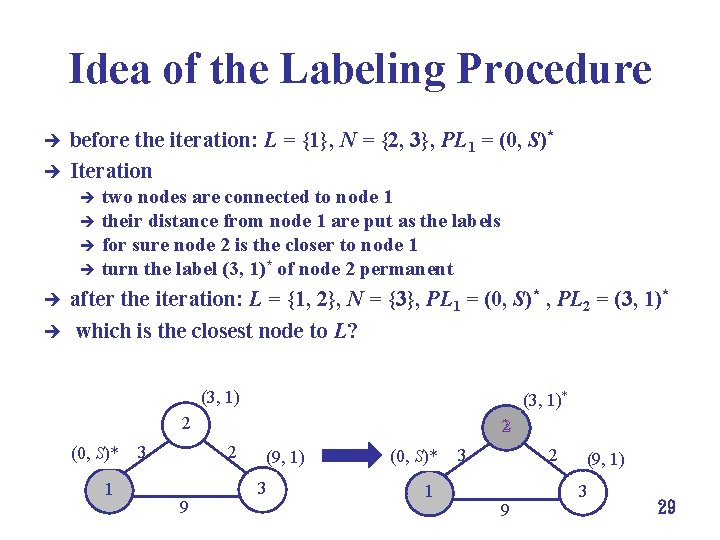
Idea of the Labeling Procedure è è before the iteration: L = {1}, N = {2, 3}, PL 1 = (0, S)* Iteration two nodes are connected to node 1 è their distance from node 1 are put as the labels è for sure node 2 is the closer to node 1 è turn the label (3, 1)* of node 2 permanent è è è after the iteration: L = {1, 2}, N = {3}, PL 1 = (0, S)* , PL 2 = (3, 1)* which is the closest node to L? (3, 1)* 2 (0, S)* 1 3 2 2 9 (9, 1) 3 (0, S)* 1 3 2 9 (9, 1) 3 29

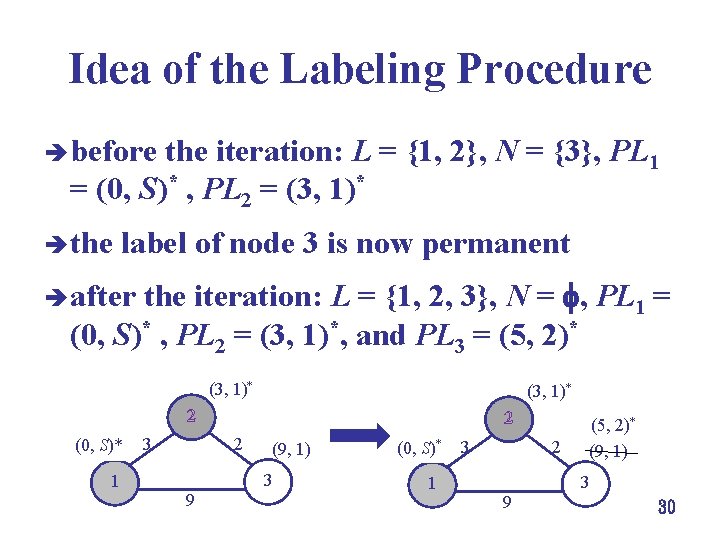
Idea of the Labeling Procedure è before the iteration: L = {1, 2}, N = {3}, PL 1 = (0, S)* , PL 2 = (3, 1)* è the label of node 3 is now permanent the iteration: L = {1, 2, 3}, N = , PL 1 = (0, S)* , PL 2 = (3, 1)*, and PL 3 = (5, 2)* è after (3, 1)* 2 (0, S)* 1 3 2 2 9 (9, 1) 3 (0, S)* 1 3 2 9 (5, 2)* (9, 1) 3 30

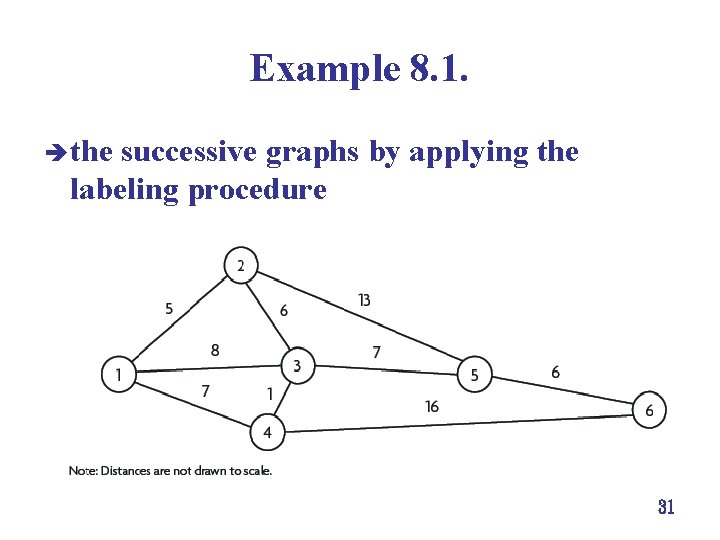
Example 8. 1. è the successive graphs by applying the labeling procedure 31

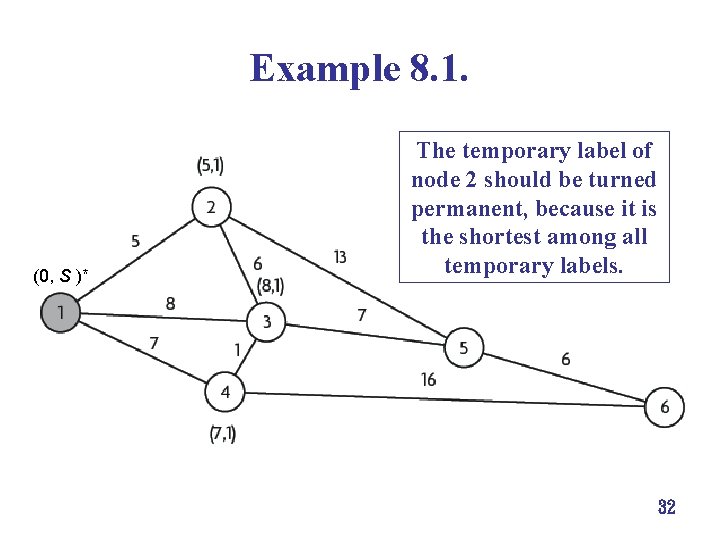
Example 8. 1. (0, S )* The temporary label of node 2 should be turned permanent, because it is the shortest among all temporary labels. 32

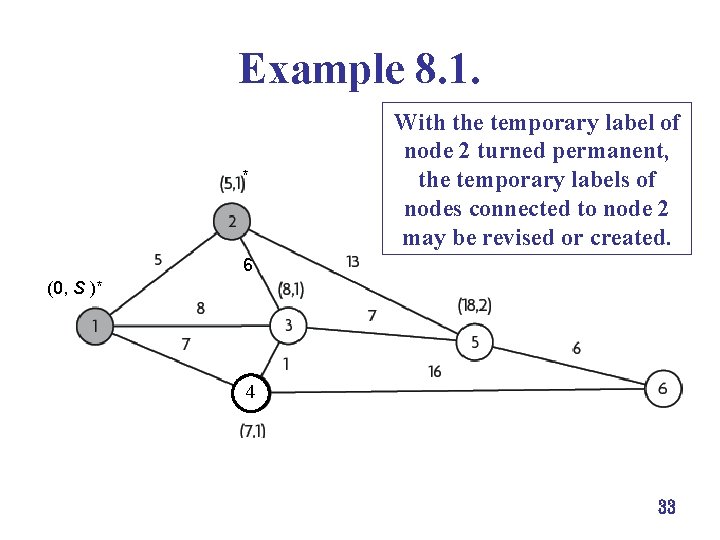
Example 8. 1. * With the temporary label of node 2 turned permanent, the temporary labels of nodes connected to node 2 may be revised or created. 6 (0, S )* * 4 33

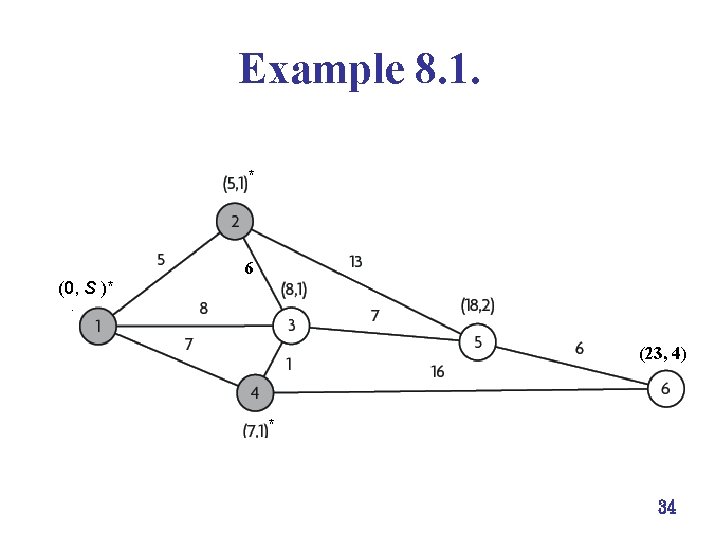
Example 8. 1. * (0, S )* 6 * (23, 4) * 34

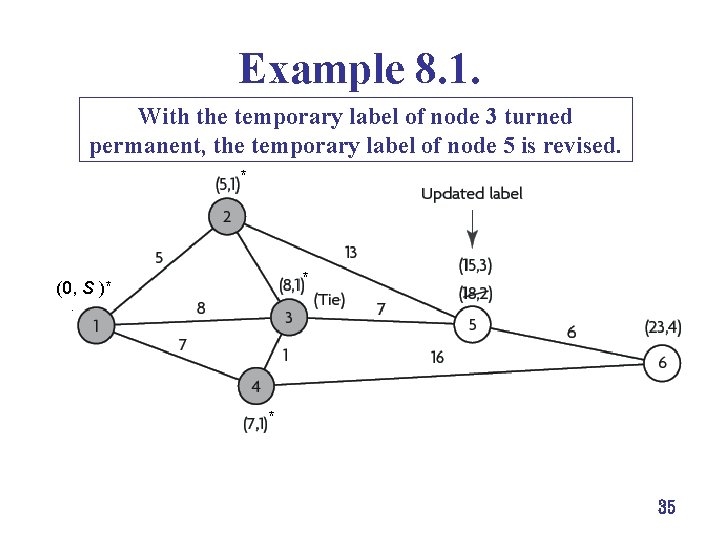
Example 8. 1. With the temporary label of node 3 turned permanent, the temporary label of node 5 is revised. * * (0, S )* * * 35

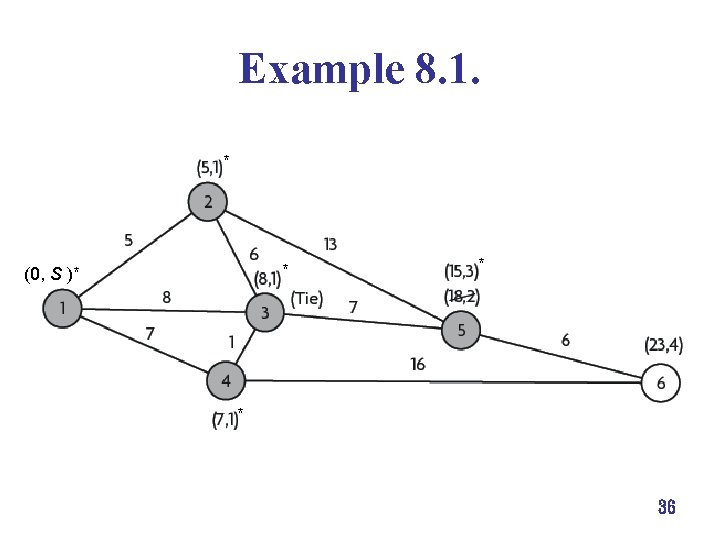
Example 8. 1. * (0, S )** * 36

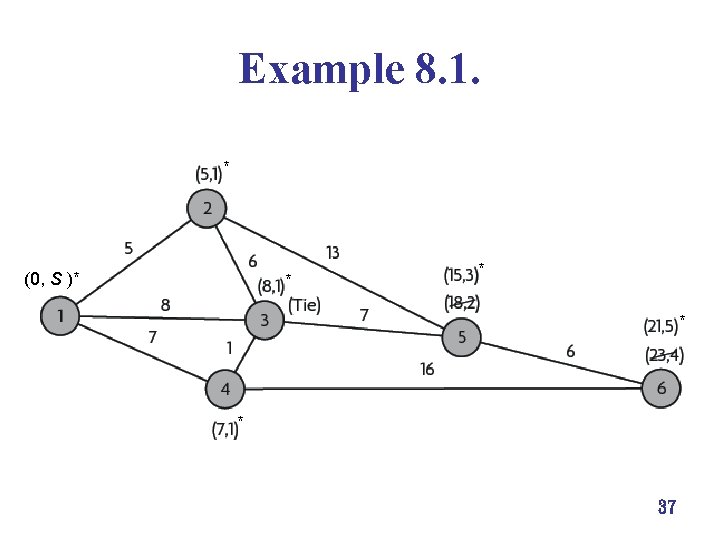
Example 8. 1. * * (0, S )* * * 37

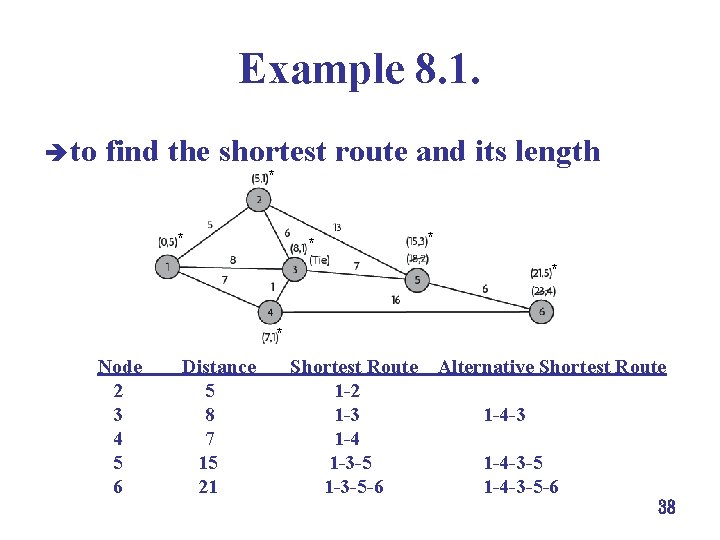
Example 8. 1. è to find the shortest route and its length * * * Node 2 3 4 5 6 Distance 5 8 7 15 21 Shortest Route 1 -2 1 -3 1 -4 1 -3 -5 -6 Alternative Shortest Route 1 -4 -3 -5 -6 38

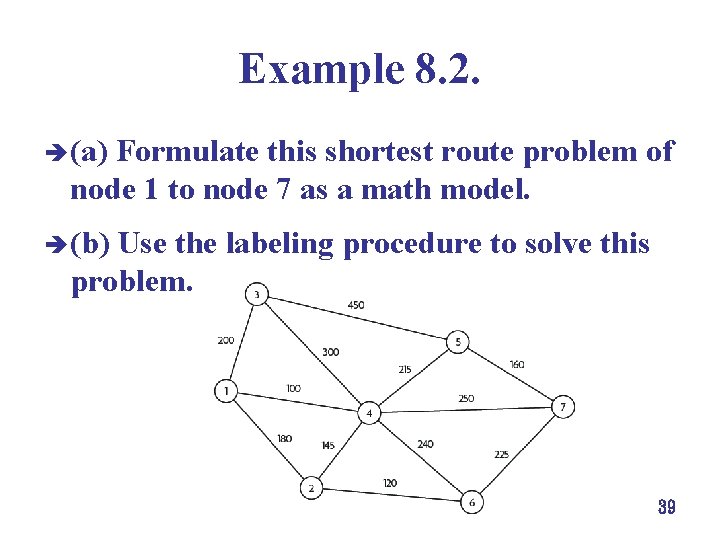
Example 8. 2. è (a) Formulate this shortest route problem of node 1 to node 7 as a math model. è (b) Use the labeling procedure to solve this problem. 39

Assignment #3 è Chapter 8 (for shortest route problems) èProblem 1 (a), (b), plus è(c) Formulate this problem as a mathematical programming model. è Possibly more problems for the next topic 41