Outline Introduction Lattice formulation Lattice QCD with Imaginary















- Slides: 29


Outline • Introduction • Lattice formulation • Lattice QCD with Imaginary Chemical Potential with Wilson Quarks • Conclusion

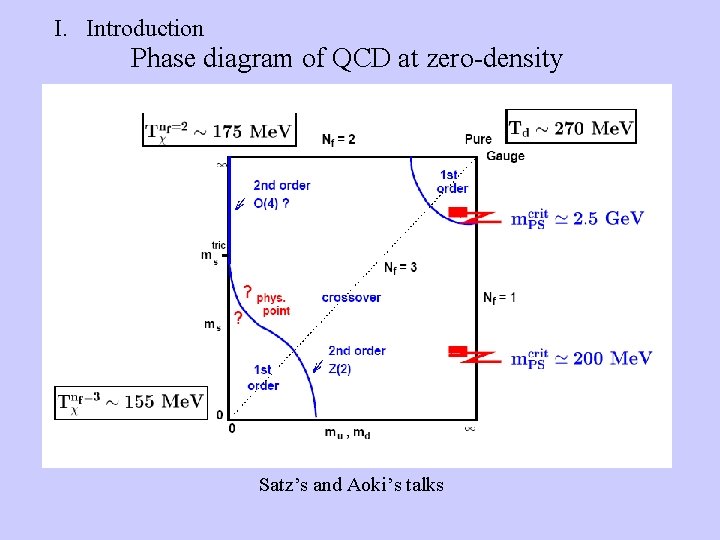
I. Introduction Phase diagram of QCD at zero-density Satz’s and Aoki’s talks

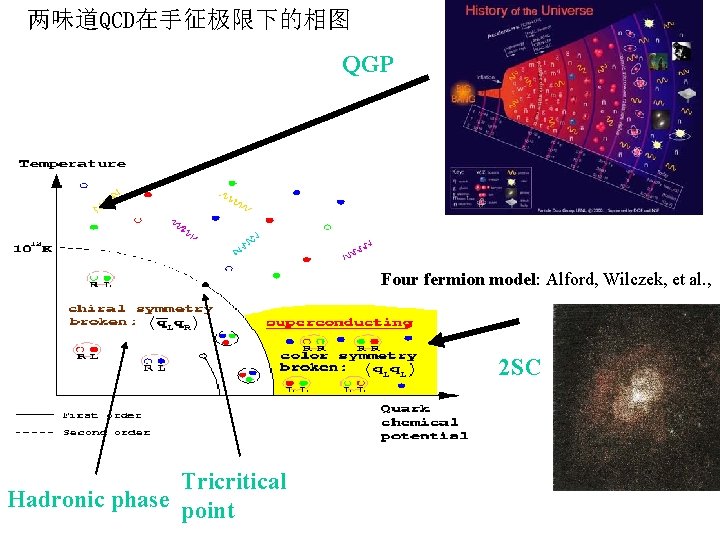
两味道QCD在手征极限下的相图 QGP Four fermion model: Alford, Wilczek, et al. , 2 SC Tricritical Hadronic phase point






解决办法 a. Improved reweighting b. Imaginary chemical potential

III. Lattice QCD with Imaginary Chemical Potential With Wilson Quarks

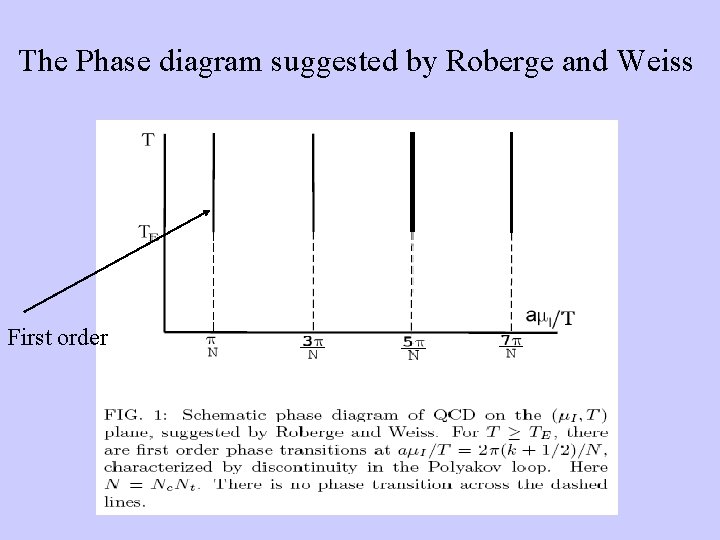
The Phase diagram suggested by Roberge and Weiss First order

Some Polyakov loop Chiral condensate observables considered

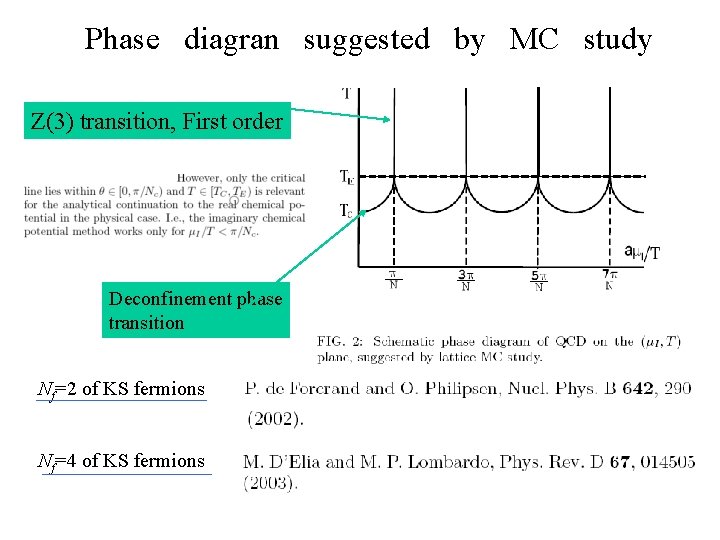
Phase diagran suggested by MC study Z(3) transition, First order Deconfinement phase transition Nf=2 of KS fermions Nf=4 of KS fermions

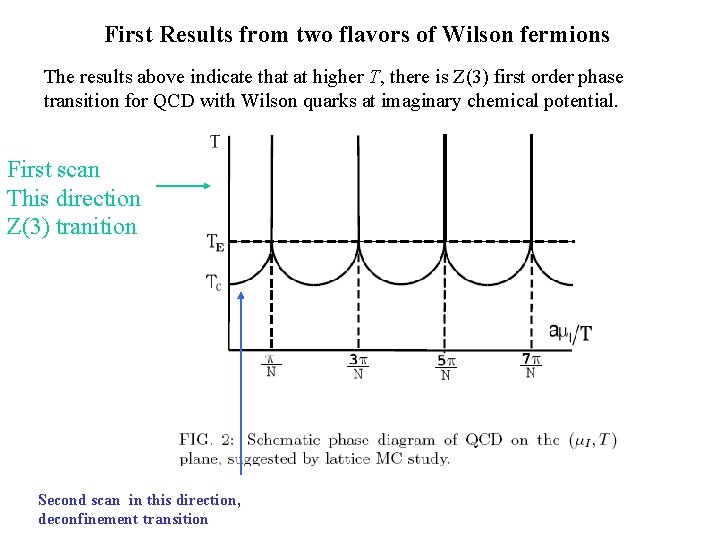
First Results from two flavors of Wilson fermions The results above indicate that at higher T, there is Z(3) first order phase transition for QCD with Wilson quarks at imaginary chemical potential. First scan This direction Z(3) tranition Second scan in this direction, deconfinement transition

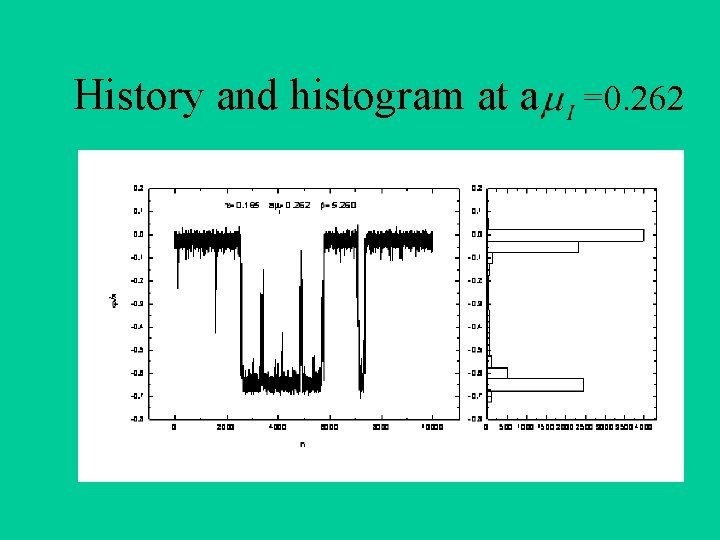
History and histogram at a =0. 262

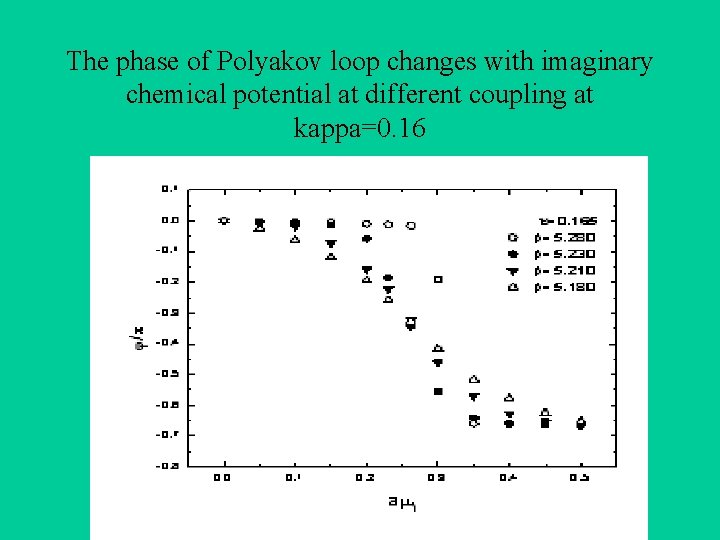
The phase of Polyakov loop changes with imaginary chemical potential at different coupling at kappa=0. 16

The determination of chiral limit • Determine the chiral limit through the axial vector Ward. Takahashi identity Y. Iwasaki, K. Kanaya, et al, Phys. Rev. Lett. 67, 1494(1991) On the lattice with

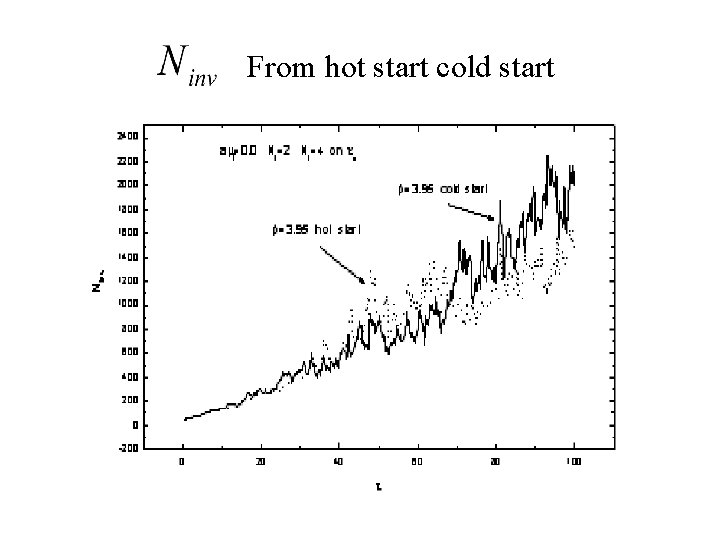
The average number of iteration for the fermionic matrix inversio Is enormously large at chiral limit in the confining phase Is of order several hundreds in the deconfining phase

From hot start cold start

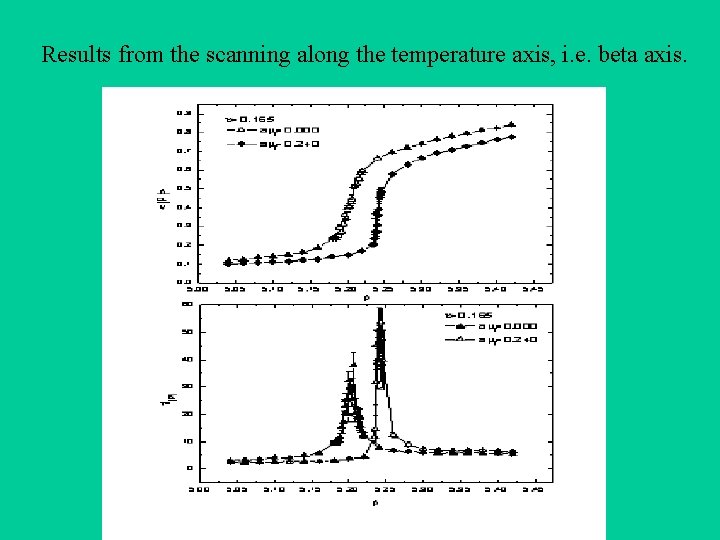
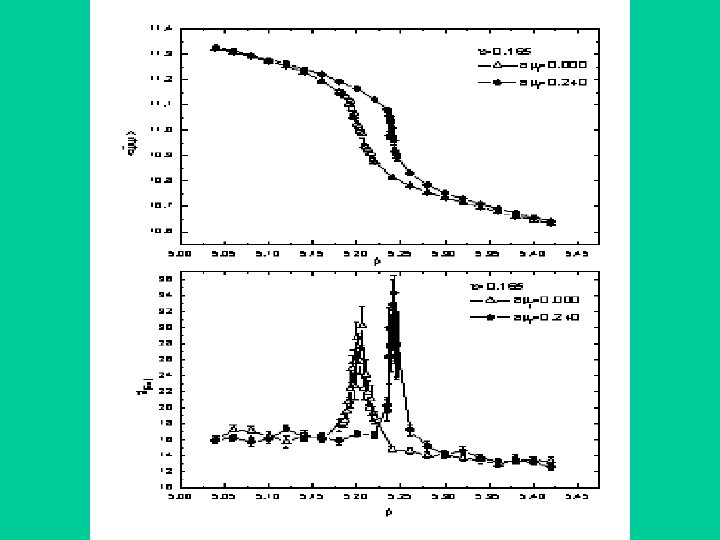
Results from the scanning along the temperature axis, i. e. beta axis.


Critical beta as a function of imaginary chemical potential To obtain critical beta as a function of real chemical potential, replace by

Using the renormalization group equation and obtain

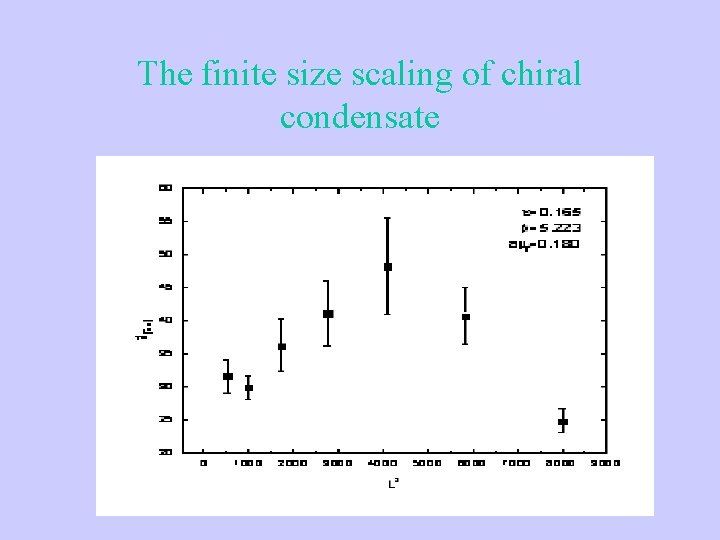
The finite size scaling of chiral condensate

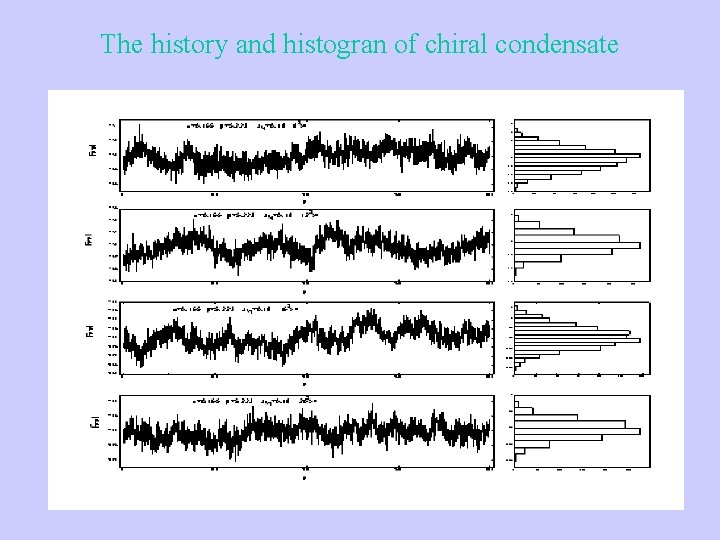
The history and histogran of chiral condensate

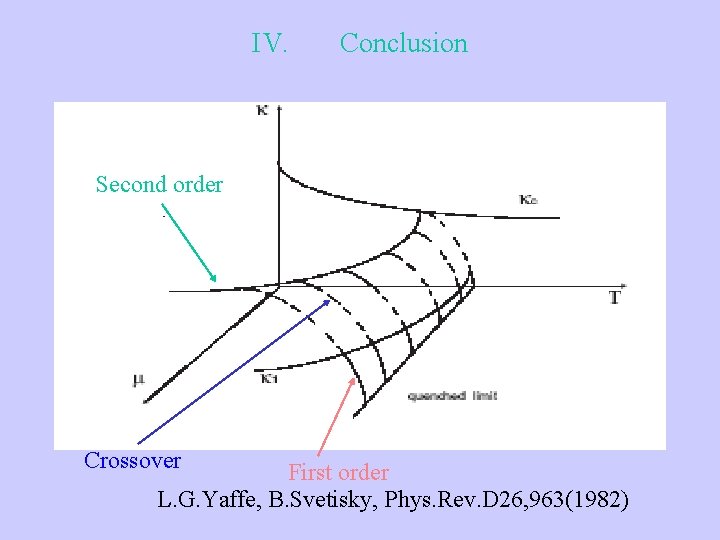
IV. Conclusion Second order Crossover First order L. G. Yaffe, B. Svetisky, Phys. Rev. D 26, 963(1982)

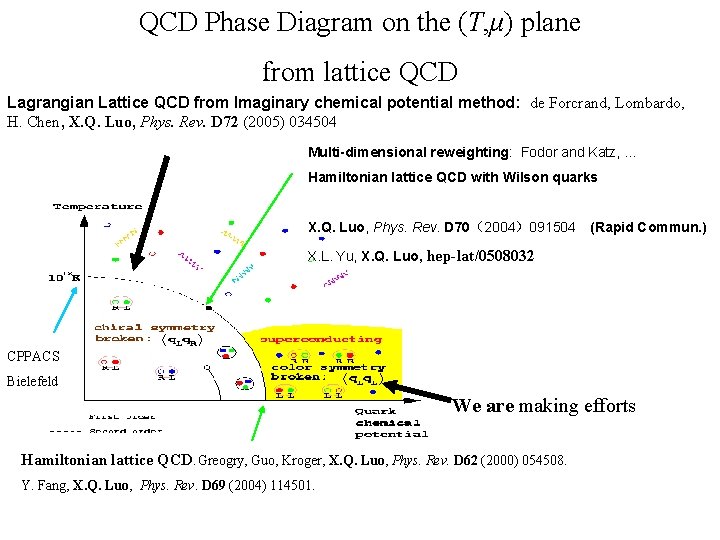
QCD Phase Diagram on the (T, μ) plane from lattice QCD Lagrangian Lattice QCD from Imaginary chemical potential method: de Forcrand, Lombardo, H. Chen, X. Q. Luo, Phys. Rev. D 72 (2005) 034504 Multi-dimensional reweighting: Fodor and Katz, … Hamiltonian lattice QCD with Wilson quarks X. Q. Luo, Phys. Rev. D 70(2004)091504 (Rapid Commun. ) X. L. Yu, X. Q. Luo, hep-lat/0508032 CPPACS Bielefeld We are making efforts Hamiltonian lattice QCD: Greogry, Guo, Kroger, X. Q. Luo, Phys. Rev. D 62 (2000) 054508. Y. Fang, X. Q. Luo, Phys. Rev. D 69 (2004) 114501.
