Outline I Why Finsler geometry II Basic concepts


Outline I. Why Finsler geometry? II. Basic concepts of Finsler geometry III. Finslerian cosmology

I. Why Finsler geometry? Components of modern cosmology § Cosmological principle § GR and particle standard model § Inflation ->(primordial scalar perturbation: adiabatic, Gaussian, nearly scale-invariant )

Signs of space anisotropy § Hemispherical asymmetry in CMB § Spatial variation of fine structure constant
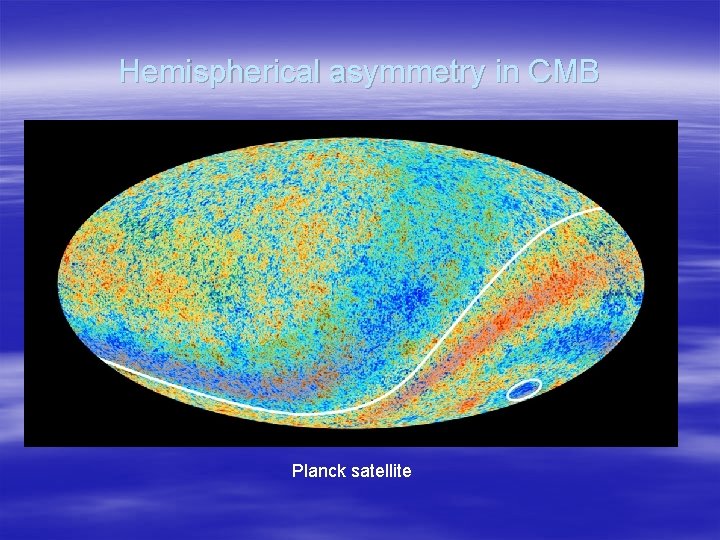
Hemispherical asymmetry in CMB Planck satellite
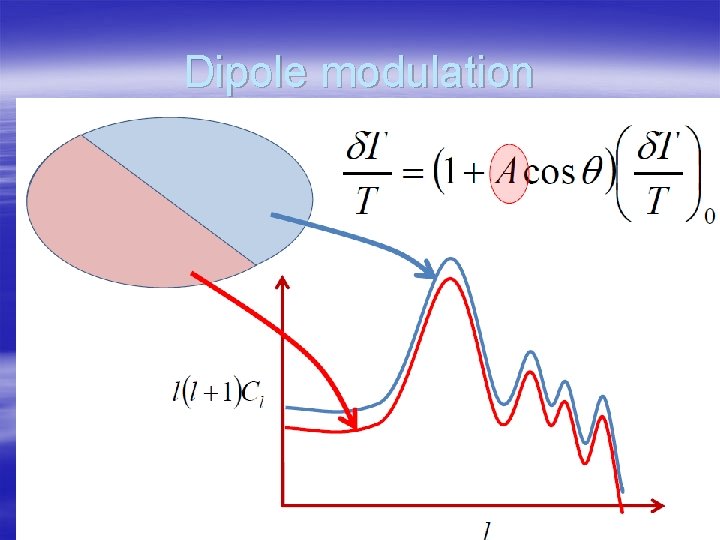
Dipole modulation
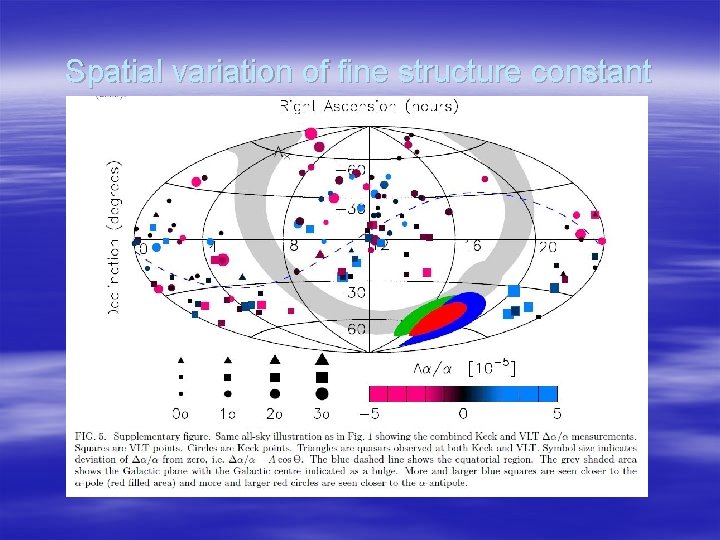
Spatial variation of fine structure constant

What if Riemann Geometry ? Finsler Geometry

II. Basic concepts of Finsler geometry Finslerian length § S. S. Chern: Finsler geometry is just Riemann geometry without the quadratic restriction § Length element: F(x, ay)=a. F(x, y) § Metric tensor: § Cartan tensor:

Three types of Finsler spacetime § Randers spacetime § Bogoslovsky spacetime(VSR) § Quartic root

Symmetry of Finsler spacetime § Isometric group § Maximum symmetry: n(n-1)/2+1(subgroup of Poincare group) § 4 dimensional constant curvature space: 6 § 4 dimensional Bogoslovsky spacetime: 8 DISIM(2) group

Geodesic and Ricci scalar § Geodesic equation (preserve F) § Ricci scalar (geometrical invariant)

Gravitational field equation in Finsler spacetime--methods § Second Bianchi identity § Action principle C. Pfeifer and M. N. R. Wohlfarth, Phys. Rev. D 85, 064009 (2012) -> § Pirani’s analogy

Geodesic deviation 场方程 真空

Geodesic deviation 真空场方程

Vacuum field equation § Finslerian geodesic deviation § Vacuum field equation

Schwarzschild-like solution Ric=0 § Properties Non-reversible Two close geodesics Busemann-Hausdorff volumm Volume equals to 4pi One independent Killing vector

III. Finslerian cosmology § Sn. Ia Hubble diagram and fine structure constant § Anisotropic inflation

Dipoles of α and Sn. Ia Hubble diagram § Back ground spacetime § Translational and x-y rotational symmetry are preserved § Gravitational field eq: where

§ Spatial variation of α § Dipoles of Hubble diagram

§ Dataset( variation ): 293+10 measurements A. M. M. Pinho, C. J. A. P. Martins, Phys. Lett. B 756, 121 (2016) § § Best fit Dipole amplitude Milky Way limit Sn. Ia Union 2. 1 dataset

Anisotropic inflation § Background spacetime § Scalar perturbed spacetime § Primordial power spectrum

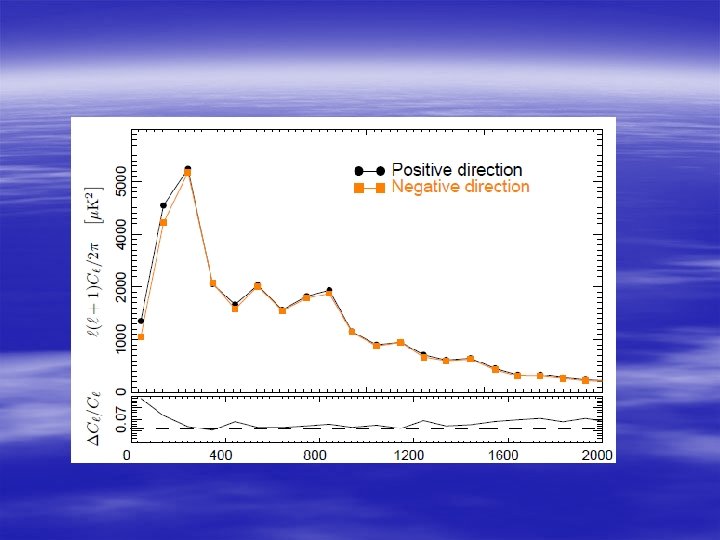
§ Dipolar modulation (2<l<600) S. Aiola, B. Wang, A. Kosowsky, T. Kahniashvili and H. Firouzjahi, Phys. Rev. D. 92, 063008 (2015) § CMB correlation coefficients § Anisotropic effect only appears in CMB correlation coefficients if l’=l+1

Conclusions and Remarks § Finsler spacetime naturally describes the anisotropic spacetime and Lorentz violation § Exist Schwarzschild-like solutions § Finslerian anisotropic inflation: anisotropic effect only appears in CMB correlation coefficients if l’=l+1

Riemann spacetime Gravitational waves Finsler spacetime

Thanks!
- Slides: 27