Outline Concept of Learning Basis of Artificial Neural

Outline • Concept of Learning • Basis of Artificial Neural Network • Neural Network with Supervised Learning (Single Layer Net) – Hebb – Perceptron – Modelling Simple Problem 1 your name TIN 5053 Neural Networks

CONCEPT OF LEARNING Nooraini Yusoff Computer Science Department Faculty of Information Technology Universiti Utara Malaysia your name TIN 5053 Neural Networks

Learning and Weights. . ? Think… Can you identify which is “the Simpsons”. your name TIN 5053 Neural Networks

Learning and Weights. . ? your name TIN 5053 Neural Networks

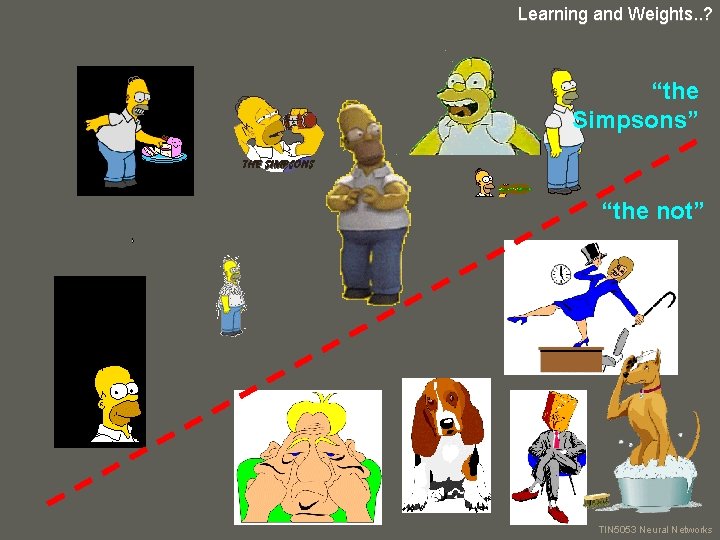
Learning and Weights. . ? “the Simpsons” “the not” your name TIN 5053 Neural Networks

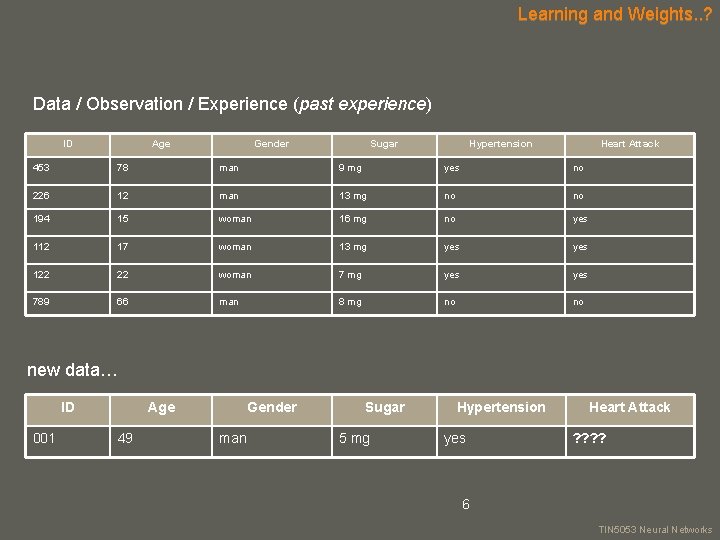
Learning and Weights. . ? Data / Observation / Experience (past experience) ID Age Gender Sugar Hypertension Heart Attack 453 78 man 9 mg yes no 226 12 man 13 mg no no 194 15 woman 16 mg no yes 112 17 woman 13 mg yes 122 22 woman 7 mg yes 789 66 man 8 mg no no new data… ID 001 Age 49 Gender man Sugar 5 mg Hypertension yes 6 Heart Attack ? ? your name TIN 5053 Neural Networks

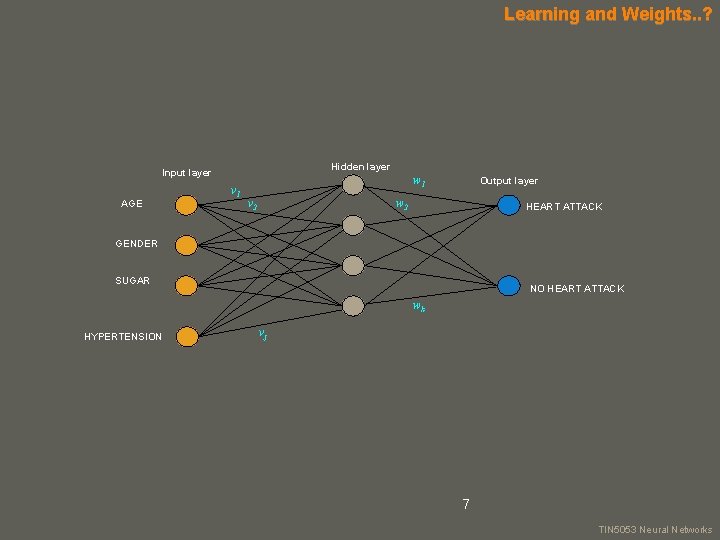
Learning and Weights. . ? Hidden layer Input layer AGE v 1 w 1 v 2 Output layer w 2 HEART ATTACK GENDER SUGAR NO HEART ATTACK wk HYPERTENSION vj 7 your name TIN 5053 Neural Networks

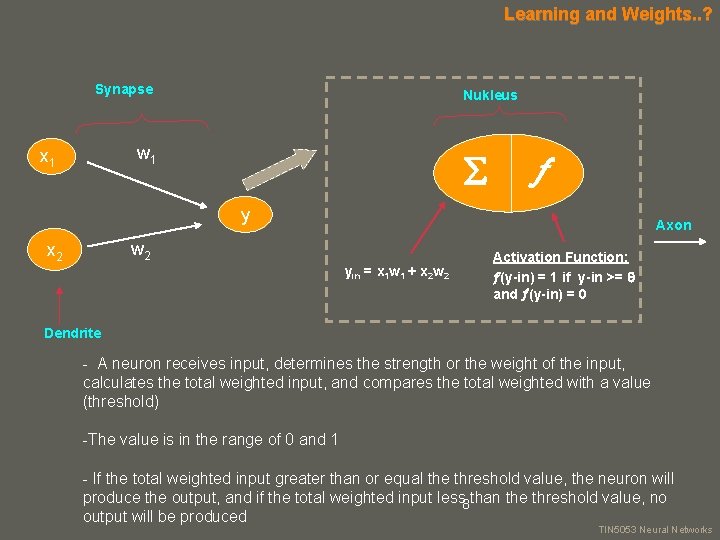
Learning and Weights. . ? Synapse Nukleus w 1 x 1 y Axon w 2 x 2 yin = x 1 w 1 + x 2 w 2 Activation Function: (y-in) = 1 if y-in >= and (y-in) = 0 Dendrite - A neuron receives input, determines the strength or the weight of the input, calculates the total weighted input, and compares the total weighted with a value (threshold) -The value is in the range of 0 and 1 - If the total weighted input greater than or equal the threshold value, the neuron will produce the output, and if the total weighted input less 8 than the threshold value, no your name output will be produced TIN 5053 Neural Networks

BASIS OF ARTIFICIAL NEURAL NETWORK Nooraini Yusoff Computer Science Department Faculty of Information Technology Universiti Utara Malaysia your name TIN 5053 Neural Networks

Basis of Artificial Neural Network (Content) • • • Data Preparation Activation Functions Biases and Threshold Weight initialization and update Linear Separability 10 your name TIN 5053 Neural Networks

Basis of Artificial Neural Network Data Preparation • In NN, inputs and outputs are to be represented numerically. • Garbage-in garbage-out principle: flawed data used in developing a network would result in a flawed network. • Unsuitable representation affects learning and could eventually turn a NN project into a failure. 11 your name TIN 5053 Neural Networks

Basis of Artificial Neural Network • Why preprocess the data? – Main goal – to ensure that the statistical distribution of values for each net input and output is roughly uniform. – NN will not produce accurate forecasts with incomplete, noisy and inconsistent data. – Decisions made in this phase of development are critical to the performance of the network. 12 your name TIN 5053 Neural Networks

Basis of Artificial Neural Network • Input & Output representation – Binary vs. Bipolar Binary [0, 1] -1 -0. 5 0 0. 5 1 Bipolar [-1, 1] 13 your name TIN 5053 Neural Networks

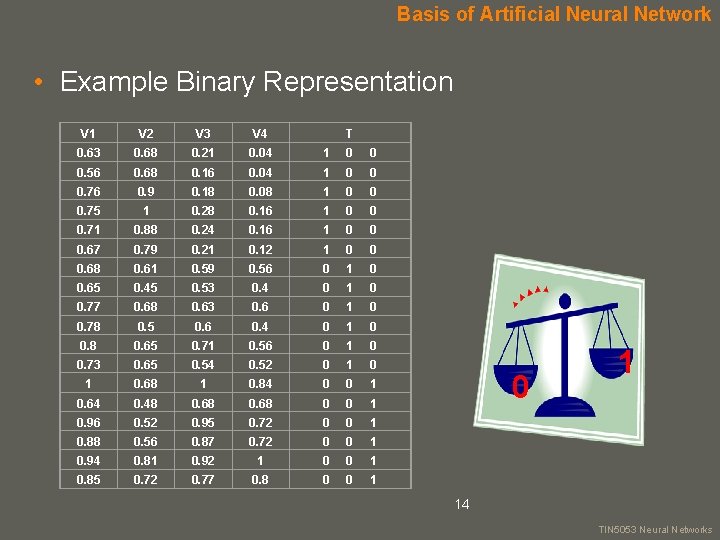
Basis of Artificial Neural Network • Example Binary Representation V 1 V 2 V 3 V 4 T 0. 63 0. 68 0. 21 0. 04 1 0 0 0. 56 0. 68 0. 16 0. 04 1 0 0 0. 76 0. 9 0. 18 0. 08 1 0 0 0. 75 1 0. 28 0. 16 1 0 0 0. 71 0. 88 0. 24 0. 16 1 0 0 0. 67 0. 79 0. 21 0. 12 1 0 0 0. 68 0. 61 0. 59 0. 56 0 1 0 0. 65 0. 45 0. 53 0. 4 0 1 0 0. 77 0. 68 0. 63 0. 6 0 1 0 0. 78 0. 5 0. 6 0. 4 0 1 0 0. 8 0. 65 0. 71 0. 56 0 1 0 0. 73 0. 65 0. 54 0. 52 0 1 0. 68 1 0. 84 0 0 1 0. 64 0. 48 0. 68 0 0 1 0. 96 0. 52 0. 95 0. 72 0 0 1 0. 88 0. 56 0. 87 0. 72 0 0 1 0. 94 0. 81 0. 92 1 0 0 1 0. 85 0. 72 0. 77 0. 8 0 0 14 1 your name TIN 5053 Neural Networks

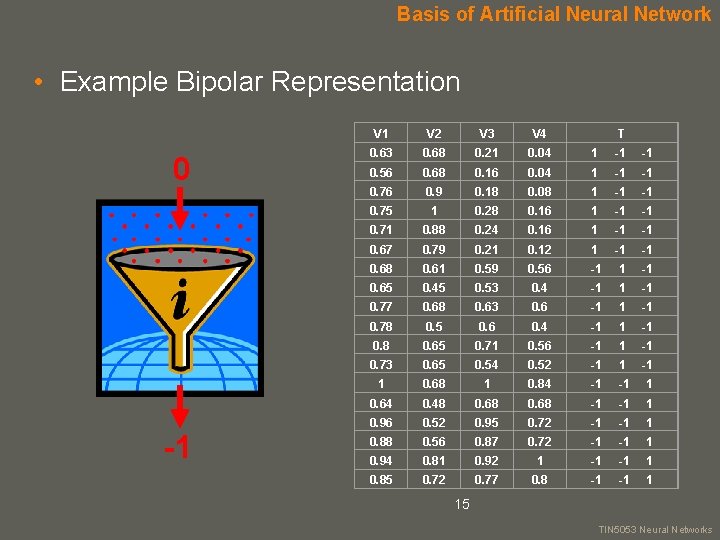
Basis of Artificial Neural Network • Example Bipolar Representation 0 -1 V 2 V 3 V 4 0. 63 0. 68 0. 21 0. 04 1 -1 -1 0. 56 0. 68 0. 16 0. 04 1 -1 -1 0. 76 0. 9 0. 18 0. 08 1 -1 -1 0. 75 1 0. 28 0. 16 1 -1 -1 0. 71 0. 88 0. 24 0. 16 1 -1 -1 0. 67 0. 79 0. 21 0. 12 1 -1 -1 0. 68 0. 61 0. 59 0. 56 -1 1 -1 0. 65 0. 45 0. 53 0. 4 -1 1 -1 0. 77 0. 68 0. 63 0. 6 -1 1 -1 0. 78 0. 5 0. 6 0. 4 -1 1 -1 0. 8 0. 65 0. 71 0. 56 -1 1 -1 0. 73 0. 65 0. 54 0. 52 -1 1 0. 68 1 0. 84 -1 -1 1 0. 64 0. 48 0. 68 -1 -1 1 0. 96 0. 52 0. 95 0. 72 -1 -1 1 0. 88 0. 56 0. 87 0. 72 -1 -1 1 0. 94 0. 81 0. 92 1 -1 -1 1 0. 85 0. 72 0. 77 0. 8 -1 -1 1 15 T your name TIN 5053 Neural Networks

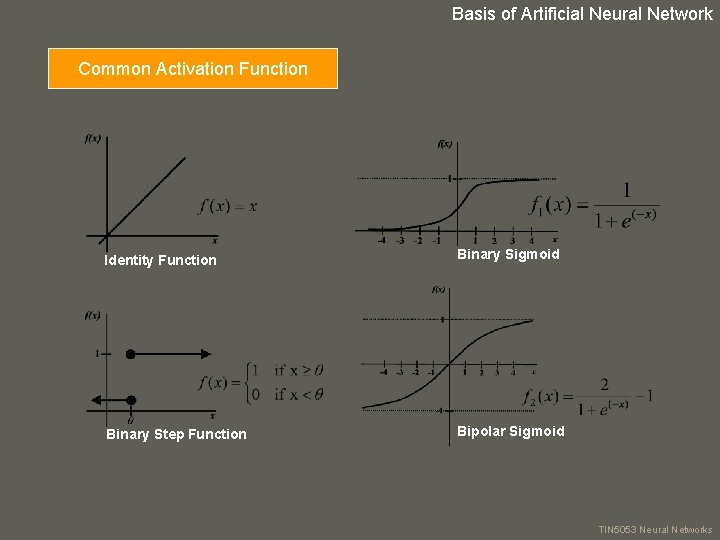
Basis of Artificial Neural Network Common Activation Function Identity Function Binary Sigmoid Binary Step Function Bipolar Sigmoid your name TIN 5053 Neural Networks

Basis of Artificial Neural Network Bias and Thresholds • A bias acts exactly as a weight on a connections from a unit whose activation is always 1. • The weight of the bias is trainable just like any other weight. • Increasing the bias increases the net input to the unit. • If a bias is included, the activation function is typically taken to be: 17 your name TIN 5053 Neural Networks

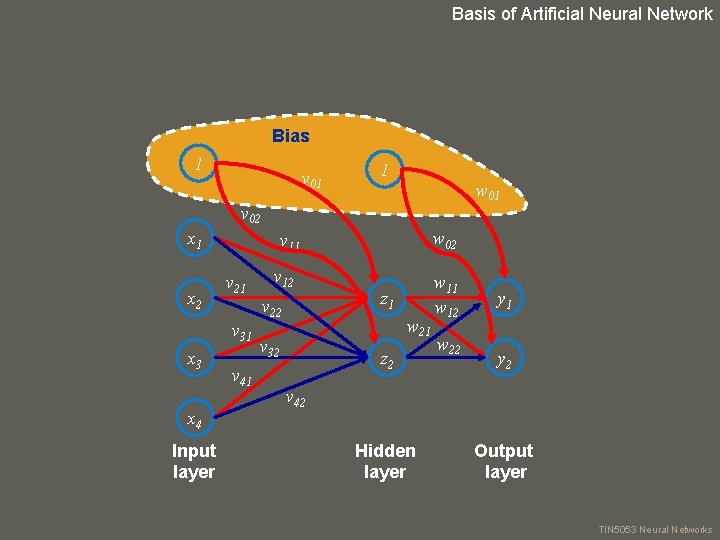
Basis of Artificial Neural Network Bias 1 v 01 1 w 01 v 02 x 1 x 2 v 21 x 4 Input layer v 12 v 22 v 31 x 3 w 02 v 11 v 41 z 1 w 21 v 32 z 2 w 11 w 12 w 22 y 1 y 2 v 42 Hidden layer Output layer your name TIN 5053 Neural Networks

Basis of Artificial Neural Network • Why use bias? . . . to increase value of yin With bias Without bias net = b + xi wi net = xi wi i i What happened if all x are 0? Learning? ? ? Yes There is A response No There is NO response 19 your name TIN 5053 Neural Networks

Basis of Artificial Neural Network Weight Initialization and Update • You may set the initial weights with any values. • The choice of initial weights will influence whether the net reaches a global (or only a local) minimum of the error and how quickly it converges. • Important to avoid choices of initial weights that would make it likely that either activations or its derivatives are zero. • Must not be too large – the initial input signals to each hidden or output unit will be likely to fall in the region where the derivative of the sigmoid func. has a very small value – saturation region. 20 your name TIN 5053 Neural Networks

Basis of Artificial Neural Network • Must not be too small – The net input to a hidden or output unit will be close to zero – cause extremely slow learning. • Methods Generating Random Weight Nguyen-Widrow Weights 21 your name TIN 5053 Neural Networks

Basis of Artificial Neural Network • Random Initialization – A common procedure is to initialize the weights (and biases) to random values between any suitable interval. • Such as – 0. 5 and 0. 5 or – 1 and 1. – The values may be +ve or –ve because the final weights after training may be of either sign also. 22 your name TIN 5053 Neural Networks

Basis of Artificial Neural Network • Nguyen-Widrow Initialization n p number of input units number of hidden units scale factor: For each hidden unit (j = 1, …, p): Initialize its weight vector (from the input units): vij(old) = random num. between – 0. 5 and 0. 5 Compute || vj(old) || 23 your name TIN 5053 Neural Networks

Basis of Artificial Neural Network Reinitialize weights: Set bias: your name TIN 5053 Neural Networks

Basis of Artificial Neural Network Linear Separability • The problem is “linear separable” – If there are weights (and a bias) so that all of the training input vectors for which the correct response is +1 lie on one side of the decision boundary and all of the training input vectors for which the correct response is – 1 lie on the other side of the decision boundary. + positive region - negative region 25 your name TIN 5053 Neural Networks

Basis of Artificial Neural Network • Problem: AND, OR, XOR 0 1 0 0 AND 1 1 0 0 OR 1 XOR 26 your name TIN 5053 Neural Networks

NEURAL NETWORK WITH SUPERVISED LEARNING (Single Layer Net) Nooraini Yusoff Computer Science Department Faculty of Information Technology Universiti Utara Malaysia 27 your name TIN 5053 Neural Networks

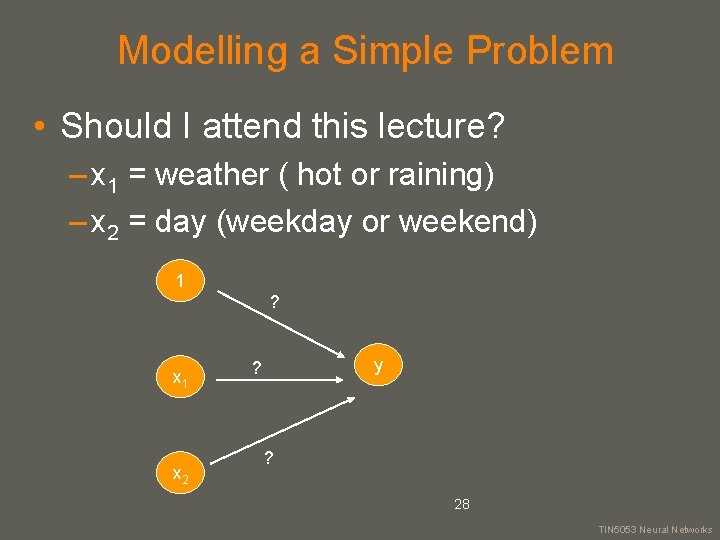
Modelling a Simple Problem • Should I attend this lecture? – x 1 = weather ( hot or raining) – x 2 = day (weekday or weekend) 1 ? x 1 x 2 y ? ? 28 your name TIN 5053 Neural Networks

Example: 2 input AND (bipolar) s 0 1 1 s 1 1 1 0 0 s 2 1 0 binary t 1 0 0 0 s 0 1 1 s 1 1 1 -1 -1 s 2 1 -1 t 1 -1 -1 -1 bipolar 29 your name TIN 5053 Neural Networks

Hebb’s Rule • 1949. Increase the weight between two neurons that are both “on”. • 1988. Increase the weight between two neurons that are both “off”. • wi(new) = wi(old) + xi*y 30 your name TIN 5053 Neural Networks

Hebb’s Algorithm 1. Set initial weights: wi = 0 for 0 <= i <= n 2. for each training vector 3. set xi = si for all input units 4. set y = t 5. wi(new) = wi(old) + xi*y 31 your name TIN 5053 Neural Networks

Training Procedure Initial weights: w 0 = 0, w 1 = 0, w 2 = 0 w 1 w 2 x 0 x 1 32 x 2 y your name TIN 5053 Neural Networks

Result Interpretation • -2 + 2 x 1 + 2 x 2 = 0 OR • x 2 = -x 1 + 1 • This training procedure is order dependent and not guaranteed. 33 your name TIN 5053 Neural Networks

Perceptrons (1958) • Very important early neural network • Guaranteed training procedure under certain circumstances 1 w 0 x 1 xn w 1 y wn 34 your name TIN 5053 Neural Networks

Activation Function • (yin) = 1 if yin > (yin) = 0 if - <= yin <= (yin) = -1 otherwise 35 your name TIN 5053 Neural Networks

Learning Rule • wi(new) = wi(old) + *t*xi • is the learning rate • Typically, 0 < <= 1 36 if error your name TIN 5053 Neural Networks

Perceptron’s Algorithm 1. 2. 3. 4. 5. 6. 7. Set initial weights: wi = 0 for 0 <= i <= n (can be random) for each training exemplar do xi = si f(yin) = 1 if yin > yin = xi*wi f(yin) = 0 if - <= yin <= f(yin) = -1 otherwise y = f(yin) wi(new) = wi(old) + *t*xi if error if stopping condition not reached, go to 2 37 your name TIN 5053 Neural Networks

Example: AND concept • • bipolar inputs bipolar target =0 =1 38 your name TIN 5053 Neural Networks

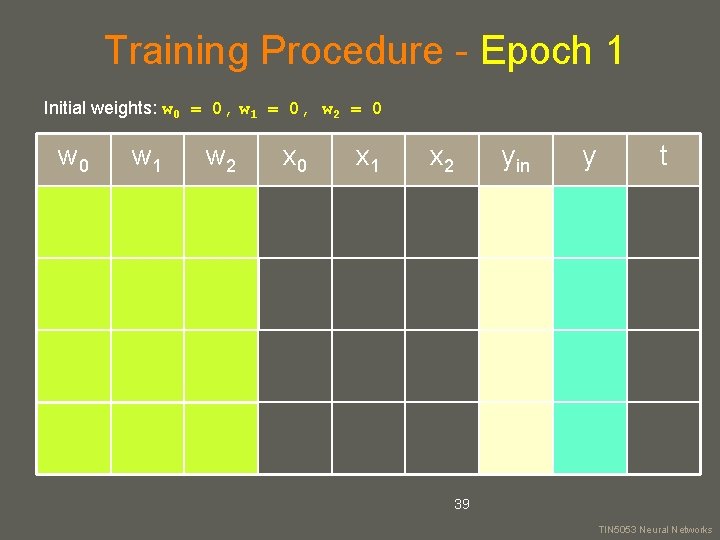
Training Procedure - Epoch 1 Initial weights: w 0 = 0, w 1 = 0, w 2 = 0 w 1 w 2 x 0 x 1 x 2 39 yin y t your name TIN 5053 Neural Networks

Exercise • Continue the above example until the learning is finished. 40 your name TIN 5053 Neural Networks

Training Procedure - Epoch 2 w 0 w 1 w 2 x 0 x 1 x 2 yin 41 y t your name TIN 5053 Neural Networks

Perceptron Learning Rule Convergence Theorem • If a weight vector exists that correctly classifies all of the training examples, then the perceptron learning rule will converge to some weight vector that gives the correct response for all training patterns. This will happen in a finite number of steps. 42 your name TIN 5053 Neural Networks

Comparison between Hebb and Perceptron Hebb Perceptron learning is not iterative Iterative learning Activation Function: -Binary step function without threshold 1 if yin ≥ 0 y = f(yin) -1 if yin < 0 Activation Function: - Binari step function with threshold 1 if yin > 0 if - <= yin <= y = f(yin) -1 if yin < - Adjustment of weights: wi(new) = wi(old) + xi*y Adjustment of weights: wi(new) = wi(old) + *t*xi Single layer net Supervised learning 43 your name TIN 5053 Neural Networks

Exercise Prepare a Perceptron learning table for epoch 1 and epoch 2 for problem of AND logic with bias using following learning requirements: - bipolar input and target - learning rate, ( ) = 1 - threshold, ( ) = 0. 2. 44 your name TIN 5053 Neural Networks

Single Layer Net (Problem Analysis) Nooraini Yusoff Universiti Utara Malaysia your name TIN 5053 Neural Networks

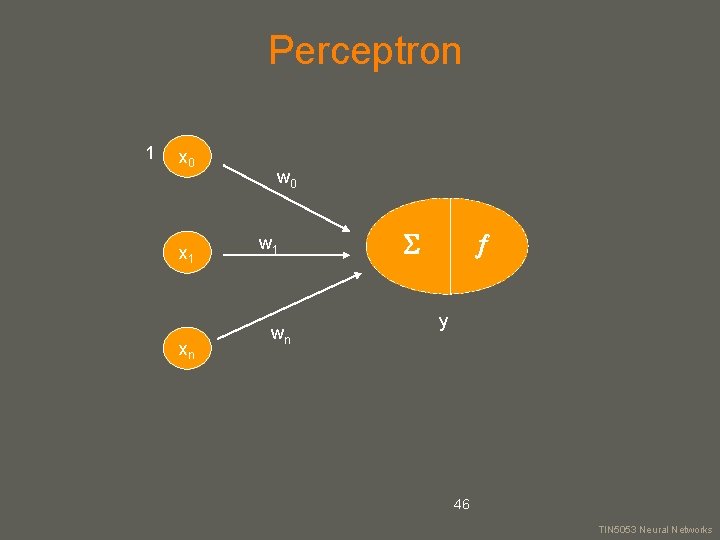
Perceptron 1 x 0 x 1 xn w 0 w 1 wn y 46 your name TIN 5053 Neural Networks

Problem Description : To predict whether an application of a student to stay in college is accepted, KIV or rejected Problem: Classification 47 your name TIN 5053 Neural Networks

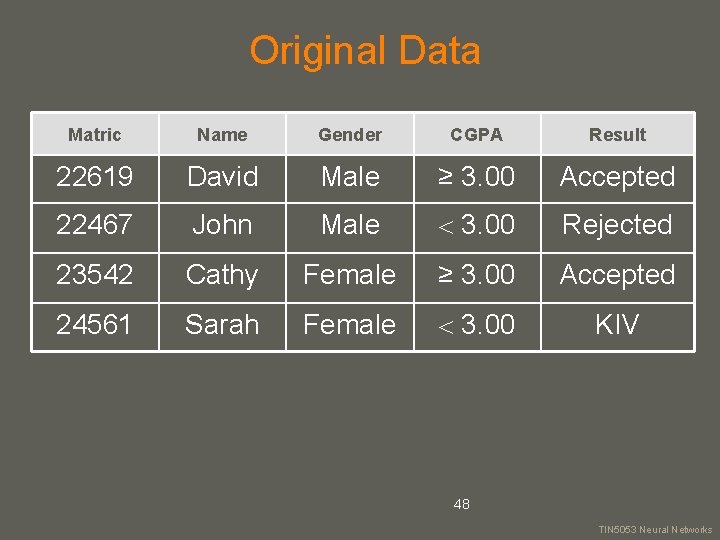
Original Data Matric Name Gender CGPA Result 22619 David Male ≥ 3. 00 Accepted 22467 John Male 3. 00 Rejected 23542 Cathy Female ≥ 3. 00 Accepted 24561 Sarah Female 3. 00 KIV 48 your name TIN 5053 Neural Networks

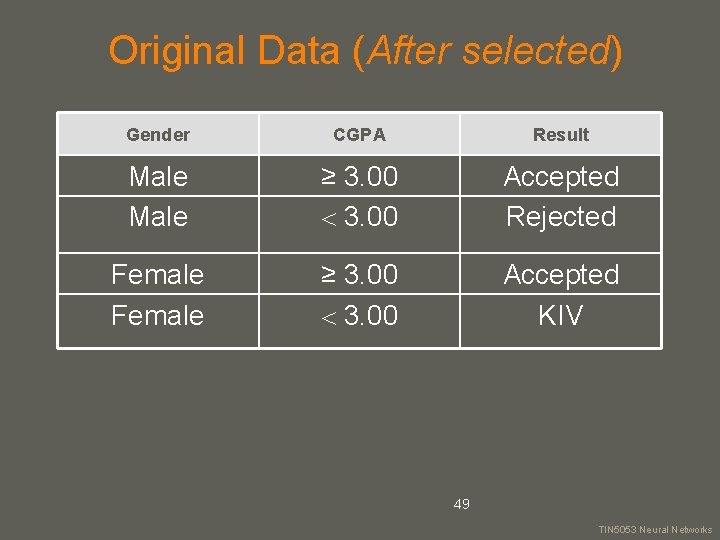
Original Data (After selected) Gender CGPA Result Male ≥ 3. 00 Accepted Rejected Female ≥ 3. 00 Accepted KIV 49 your name TIN 5053 Neural Networks

Representation of Data Male ( 1 ) Gender Female ( -1 ) ≥ 3. 00 ( 1 ) CGPA 3. 00 ( -1 ) Gender CGPA Result 1 1 -1 -1 1 0 Accepted ( 1 ) Result Data for learning KIV ( 0 ) Rejected ( -1 ) 50 your name TIN 5053 Neural Networks

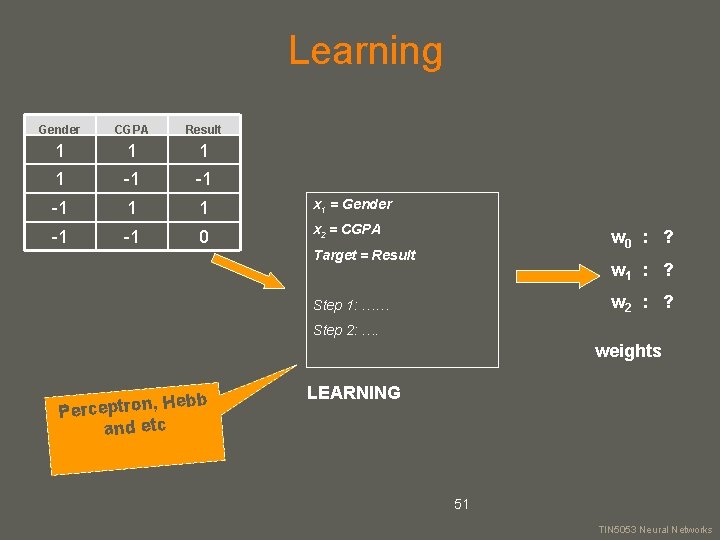
Learning Gender CGPA Result 1 1 -1 -1 -1 1 1 x 1 = Gender -1 -1 0 x 2 = CGPA w 0 : ? Target = Result w 1 : ? w 2 : ? Step 1: …… Step 2: …. weights Hebb Perceptron, and etc LEARNING 51 your name TIN 5053 Neural Networks

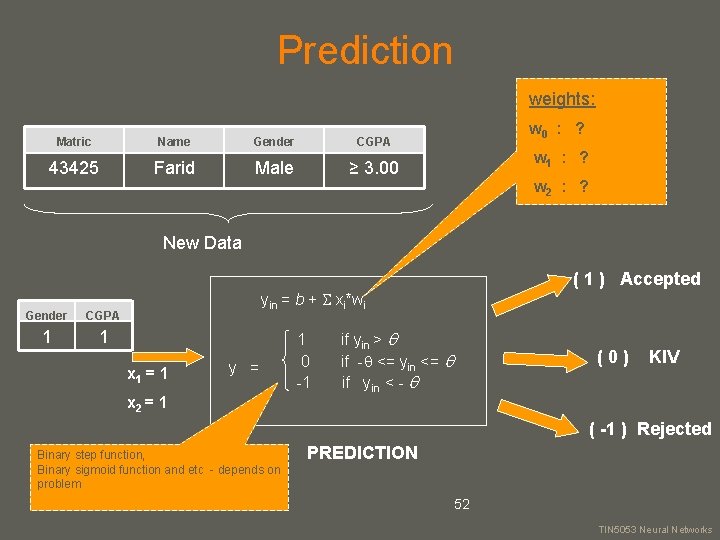
Prediction weights: Matric Name Gender CGPA 43425 Farid Male ≥ 3. 00 w 0 : ? w 1 : ? w 2 : ? New Data Gender CGPA 1 1 ( 1 ) Accepted yin = b + xi*wi x 1 = 1 y = x 2 = 1 1 0 -1 if yin > if - <= yin <= if yin < - (0) KIV ( -1 ) Rejected Binary step function, Binary sigmoid function and etc - depends on problem PREDICTION 52 your name TIN 5053 Neural Networks