Outline Boolean Logic FirstOrder Logic What is Logic

大綱 Outline • Boolean Logic (布林邏輯) • First-Order Logic (一階邏輯)

何謂邏輯? What is Logic ? • A world of true and false. • Data –T , F • Function – And (&) – Or (|) – Not (-)

邏輯系統的種類 Types of Logic • Propositional logic (命題邏輯) – Also known as Boolean Logic (§ 1. 1 -1. 2): – Basic definitions. (§ 1. 1) – Equivalence rules & derivations. (§ 1. 2) • Predicate logic (述詞邏輯 或 謂詞邏輯) – Also known as First-Order Logic (§ 1. 3 -1. 4) – Predicates. – Quantified predicate expressions. – Equivalences & derivations.

述詞邏輯 Propositional Logic is the logic of compound statements built from simpler statements using so-called Boolean connectives. Some applications in computer science: • Design of digital electronic circuits. • Expressing conditions in programs. • Queries to databases & search engines. George Boole (1815 -1864)

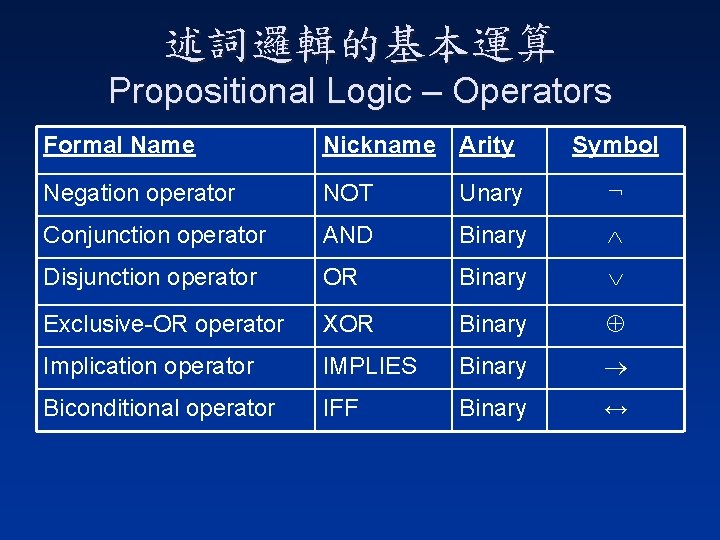
述詞邏輯的基本運算 Propositional Logic – Operators Formal Name Nickname Arity Symbol Negation operator NOT Unary ¬ Conjunction operator AND Binary Disjunction operator OR Binary Exclusive-OR operator XOR Binary Implication operator IMPLIES Binary Biconditional operator IFF Binary ↔

運算一：反相 Negation operator - NOT

運算二：及 Conjunction operator – AND

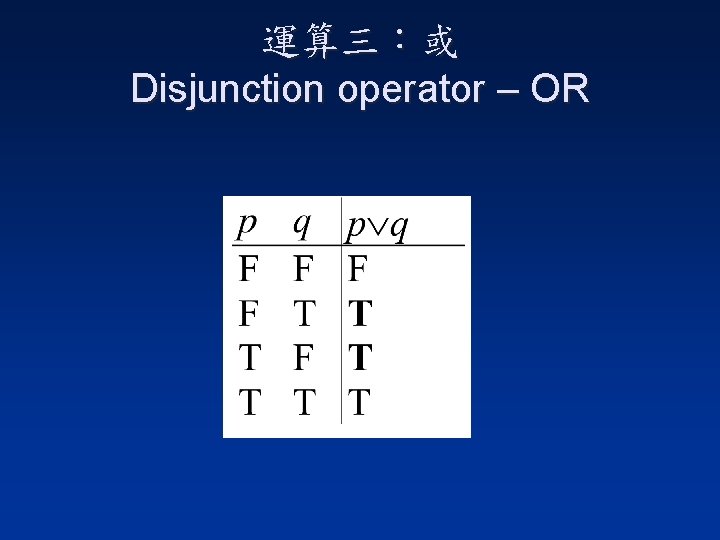
運算三：或 Disjunction operator – OR

述詞邏輯的表示式 Expressions of Propositional Logic • Use parentheses to group sub-expressions – Example : • m : male • c : child • m c : male child (boy) – Example : • f (g s)

運算四：互斥或 Exclusive-Or – XOR

自然語言的語義不清楚 Natural Language is Ambiguous Note that English “or” can be ambiguous regarding the “both” case! “Pat is a singer or Pat is a writer. ” “Pat is a man or Pat is a woman. ” Need context to disambiguate the meaning! For this class, assume “or” means inclusive.

運算五：導致 The Implication Operator • p q means p implies q. – If p is true, then q is true; – but if p is not true, then q could be either true or false. • Example : – E. g. , let p = “You study hard. ” q = “You will get a good grade. ” – p q = “If you study hard, then you will get a good grade. ” (else, it could go either way)

p q 的真值表 Implication Truth Table • p q is false only when p is true but q is not true. • p q does not say that p causes q! • p q does not require that p or q are ever true! • E. g. “(1=0) pigs can fly” is TRUE!

Imply 運算 的範例 Examples of Implications • “If this lecture ends, then the sun will rise tomorrow. ” True or False? • “If Tuesday is a day of the week, then I am a penguin. ” True or False? • “If 1+1=6, then Bush is president. ” True or False? • “If the moon is made of green cheese, then I am richer than Bill Gates. ” True or False?

三種反運算 Converse, Inverse, Contrapositive Some terminology, for an implication p q: • Its converse is: q p. • Its inverse is: ¬p ¬q. • Its contrapositive: ¬q ¬ p. • One of these three has the same meaning (same truth table) as p q. Can you figure out which?

p q = -q -p 兩者相等 How do we know for sure? Proving the equivalence of p q and its contrapositive using truth tables:

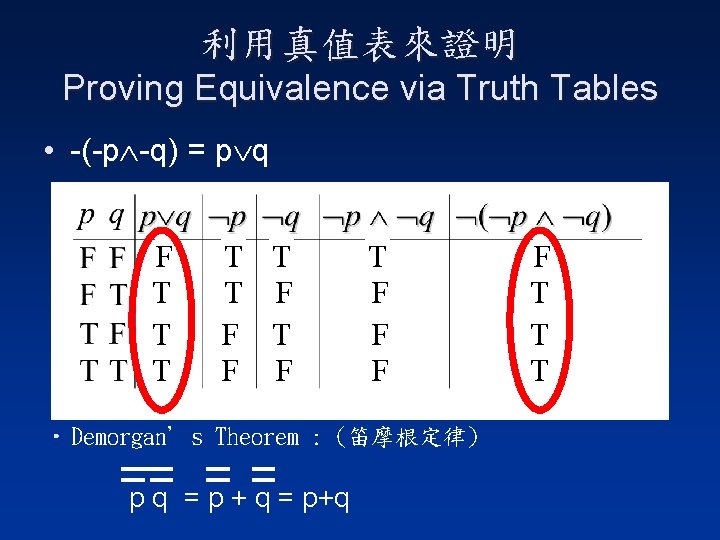
利用真值表來證明 Proving Equivalence via Truth Tables • -(-p -q) = p q Ex. Prove that p q ( p q). F T T T F F T T F F F T • Demorgan’s Theorem : (笛摩根定律) p q = p + q = p+q

p q 的真值表 Biconditional Truth Table • p q means that p and q have the same truth value. • Note this truth table is the exact opposite of ’s! – p q means ¬(p q) • p q does not imply p and q are true, or cause each other.

布林運算總整理 Boolean Operations Summary • We have seen 1 unary operator (out of the 4 possible) and 5 binary operators (out of the 16 possible). Their truth tables are below.

布林運算的幾種符號表達法 Some Alternative Notations

位元運算 Bits and Bit Operations • A bit is a binary (base 2) digit: 0 or 1. John Tukey (1915 -2000) • Bits may be used to represent truth values. • By convention: 0 represents “false”; 1 represents “true”. • Boolean algebra is like ordinary algebra except that variables stand for bits, + means “or”, and multiplication means “and”. – See chapter 10 for more details.

布林代數的基本運算 Boolean Operator • Boolean Complement (-) 1=0 • Boolean Sum (+) 1+1=1 1+0=1 0+1=1 0+0=0 0=1 • Boolean Product (‧) 1‧ 1=1 1‧ 0=0 0‧ 1=0 0‧ 0=0

布林集合 Boolean Set • Boolean Set : B – B = {0, 1} – Example : 0 • n tuple boolean set – Bn = {(x 1, x 2, …, xn)| xi B for 1 i n} – Example : • • (0, 0) (0, 1) (1, 0) (1, 1)

布林變數 Boolean Variable • The variable x is called a boolean variable if it assume values only from B, that is , if its only possible value are 0 and 1.

布林代數式 Boolean Expression • Boolean expression – 0, 1, x 2, …, xn – If E 1 and E 2 are Boolean expression, then the following expressions are boolean expressions • E 1 • (E 1 E 2) • (E 1+E 2) • Example : – – 0 x (1+x) (x+y)(zy) Counter example (反例） xy+)(+z

布林函數 Boolean Function (1) • Boolean function of degree n – A function mapping from Bn to B • Example : – f(x, y) = xy

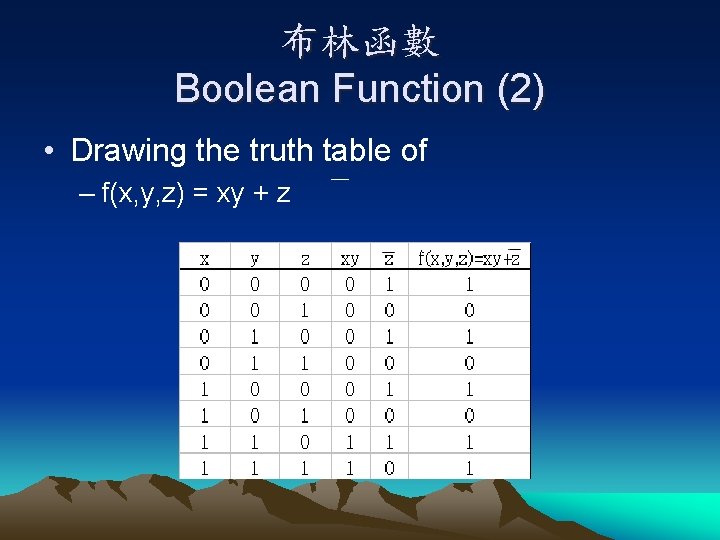
布林函數 Boolean Function (2) • Drawing the truth table of – f(x, y, z) = xy + z

Some Applications of Boolean Logic 陳鍾誠 2006 年於金門

布林邏輯的應用 Applications of Boolean Logic • Circuit Design : – Building Truth Table – Minimizing the number of circuit • By Karnaugh Maps (卡諾圖) • Database Querying • Logical Inference in Artificial Intelligence – An extension of Boolean Logic called First-Order Logic • Example : Prolog,

電路設計中的布林代數 Boolean Algebra in Circuit Design • Truth Table (真值表) • Karnaugh Maps (卡諾圖)

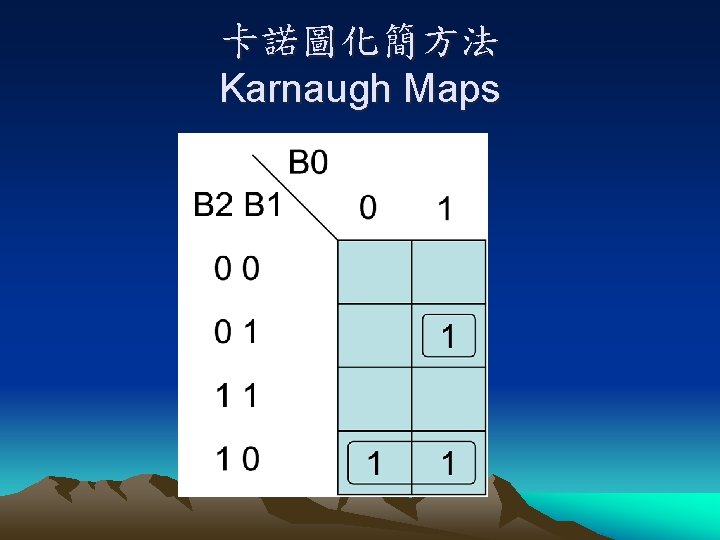
卡諾圖化簡方法 Karnaugh Maps

ＱＭ布林化簡法 Quine-Mc. Cluskey Method • Minimizing the boolean expression with any number of variable (10. 4, pp. 727).

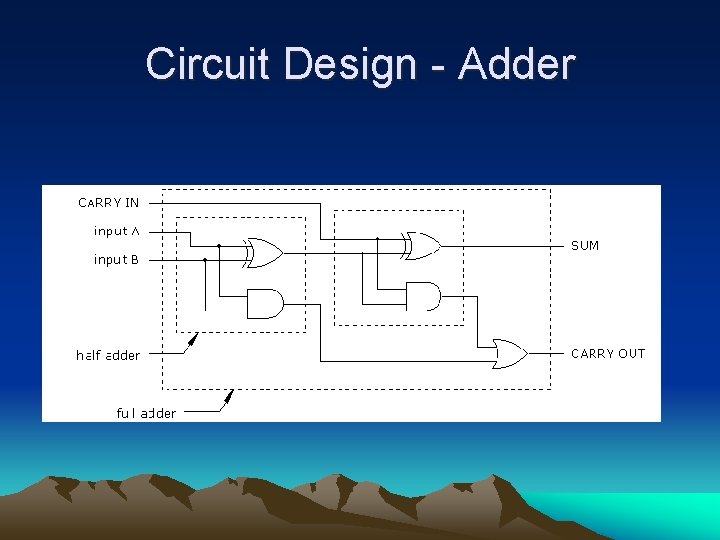
Circuit Design - Adder

邏輯推論 Logical Reasoning 陳鍾誠 2006 年於金門

邏輯推論的歷史 History of Proof System • Aristotle • Boole • Hilbert • Gentzen • Robinson

亞里斯多德 Aristotle • 三段論 – http: //zh. wikipedia. org/wiki/%E 9%A 1%B 9%E 9 %80%BB%E 8%BE%91

型式 1 P Q Q R P R

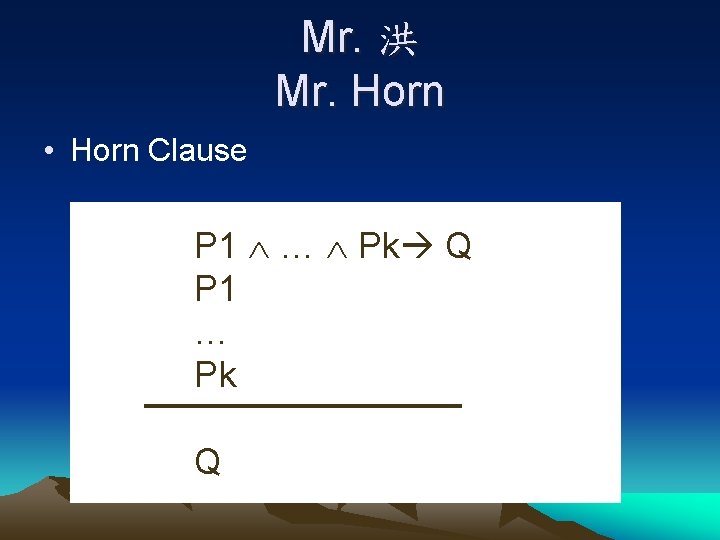
Mr. 洪 Mr. Horn • Horn Clause P 1 … Pk Q P 1 … Pk Q

Hilbert • Modus Ponens

Hilbert’s Axiom

Gentzen • Axioms and Rules of Inference

Gentzen’s Rules (1) • Disjunction rules • Conjunction rules

Gentzen’ Rules (2) • Implication rules • Negation rule

Completeness • Gentzen’s Rules are complete – All logical theorem can be proofed from these rules.

Robinson • Resolution Proof : P Q ; Q R -P R

Robinson – second form -P Q ; Q R P R

Completeness • Robinson’s Rule is Complete under the resolution procedure. • Refutation – Proof by contradiction

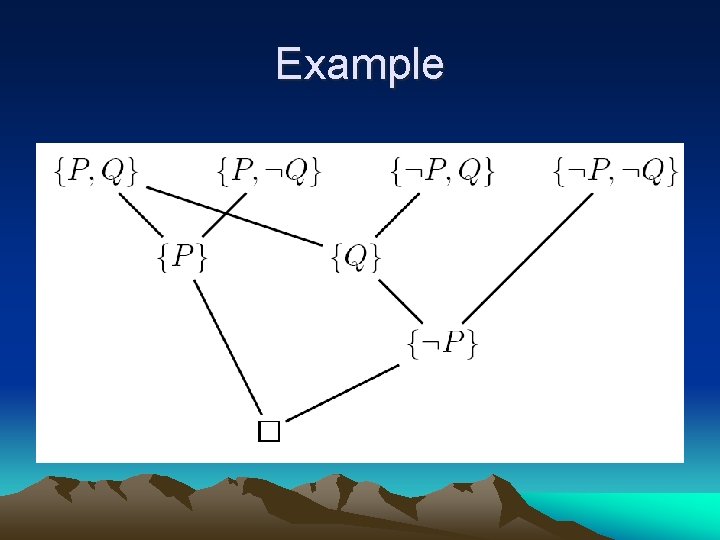
Example

Question P Q Q S -P R R S Is S true under these rules ?

Question in -P Q -Q S - P R -R S

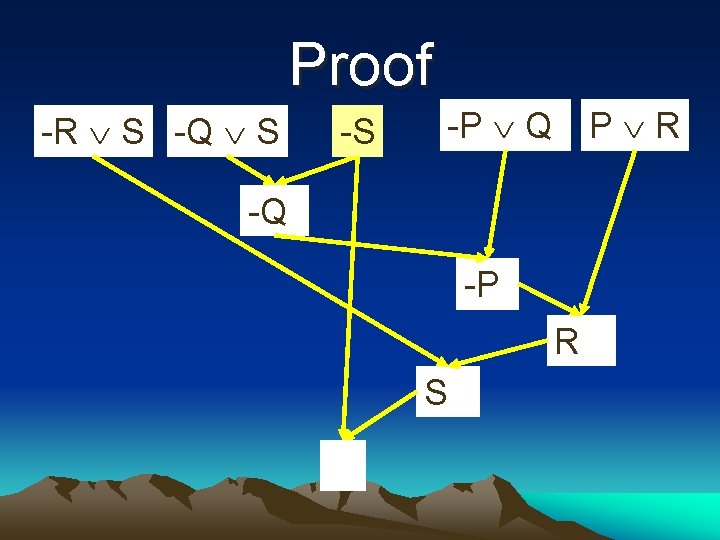
Proof -R S -Q S -S -P Q P R -Q -P R S

Reference • Symbolic Logic – http: //en. wikipedia. org/wiki/Symbolic_logic • 三段論 – http: //zh. wikipedia. org/wiki/%E 4%B 8%89%E 6 %AE%B 5%E 8%AB%96

相等關係的推導 Equivalence Laws • These are similar to the arithmetic identities you may have learned in algebra, but for propositional equivalences instead. • They provide a pattern or template that can be used to match all or part of a much more complicated proposition and to find an equivalence for it.

相等關係的範例 (1) Equivalence Laws - Examples • Identity: p T p p F p • Domination: p T T p F F • Idempotent: p p p

相等關係的範例 (2) Equivalence Laws - Examples • Double negation: p p • Commutative: p q q p • Associative: (p q) r p (q r)

更多的相等關係 (1) More Equivalence Laws • Distributive: p (q r) (p q) (p r) • De Morgan’s: (p q) p q Augustus De Morgan (1806 -1871)

更多的相等關係 (2) More Equivalence Laws • Trivial tautology/contradiction: p p T p p F

以相等關係做為運算的定義(1) Defining Operators via Equivalences Using equivalences, we can define operators in terms of other operators. • Exclusive or: p q (p q) (q p)

以相等關係做為運算的定義(2) Defining Operators via Equivalences • Implies: p q • Biconditional: p q (p q) (q p) p q (p q)

一個很長推論的範例 An Example Problem • Check using a symbolic derivation whether (p q) (p r) p q r. (p q) (p r) [Expand definition of ] (p q) (p r) [Defn. of ] (p q) ((p r) (p r)) [De. Morgan’s Law] ( p q) ((p r) (p r)) [associative law] cont.

繼續推論… Example Continued. . . ( p q) ((p r) (p r)) [ commutes] (q p) ((p r) (p r)) [ associative] q ( p ((p r) (p r))) [distrib. over ] q ((( p (p r)) ( p (p r))) [assoc. ] q ((( p p) r) ( p (p r))) [trivail taut. ] q ((T r) ( p (p r))) [domination] q (T ( p (p r))) [identity] q ( p (p r)) cont.

終於推導完畢 End of Long Example q ( p (p r)) [De. Morgan’s] q ( p r)) [Assoc. ] q (( p p) r) [Idempotent] q ( p r) [Assoc. ] (q p) r [Commut. ] p q r Q. E. D. (quod erat demonstrandum)

回顧：述詞邏輯 • Atomic propositions: p, q, r, … • Boolean operators: • Compound propositions: s : (p q) r • Equivalences: p q (p q) • Proving equivalences using: – Truth tables. – Symbolic derivations. p q r …