Outer SPACE An Outer Product based Sparse Matrix

Outer. SPACE An Outer Product based Sparse Matrix Multiplication Accelerator 28 February, 2018 Subhankar Pal, Jonathan Beaumont, Dong-Hyeon Park, Aporva Amarnath, Siying Feng, Chaitali Chakrabarti†, Hun-Seok Kim, David Blaauw, Trevor Mudge and Ronald Dreslinski University of Michigan, Ann Arbor †Arizona State University HPCA 3/12/18 2018 1

Overview Introduction Algorithm Architecture Evaluation Conclusion HPCA 3/12/18 2018 2 2

Overview Introduction Algorithm Architecture Evaluation Conclusion HPCA 3/12/18 2018 3 3

The Big Data Problem Big data collected from various sources Sensor feed, social media, scientific experiments Challenge: the nature of data is sparse Architecture research previously focused on improving compute Sparse matrix computation: a key example of memory bound workloads GPUs achieve ~100 GFLOPS for dense matrix mult. vs. ~100 MFLOPS for sparse Two dominant kernels Sparse matrix-matrix multiplication (Sp. GEMM) Breadth-first search, algebraic multigrid methods Sparse matrix-vector multiplication (Sp. MV) Page. Rank, support vector machines, ML based text analytics HPCA 3/12/18 2018 4 4

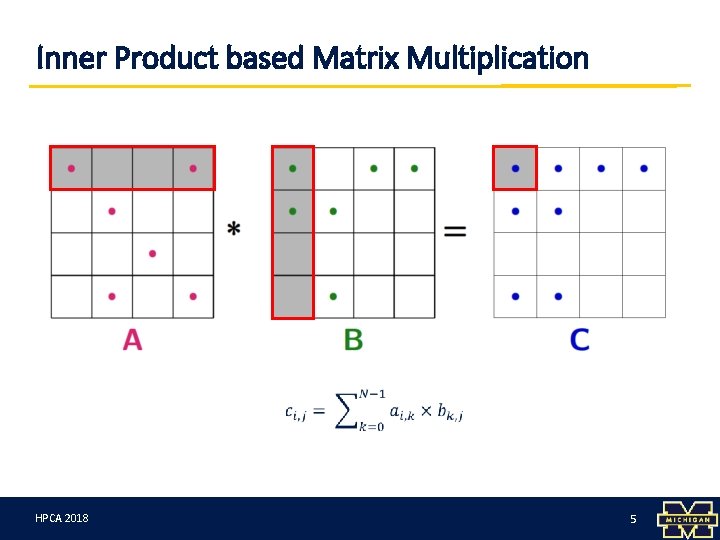
Inner Product based Matrix Multiplication HPCA 3/12/18 2018 5 5

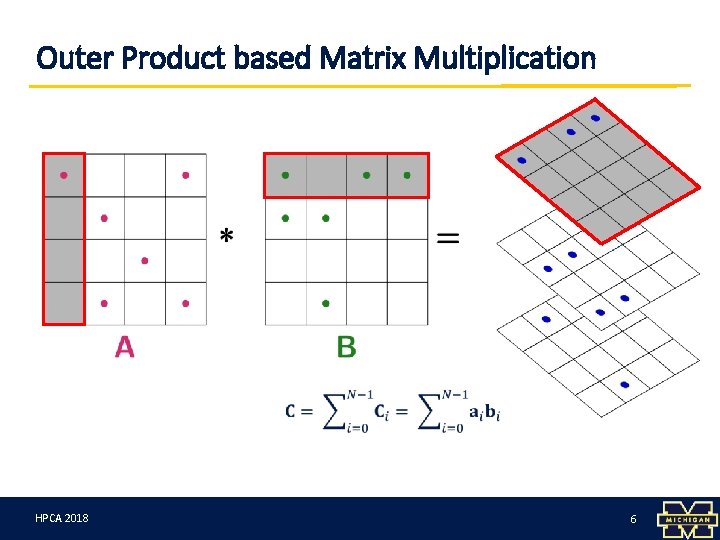
Outer Product based Matrix Multiplication HPCA 3/12/18 2018 6 6

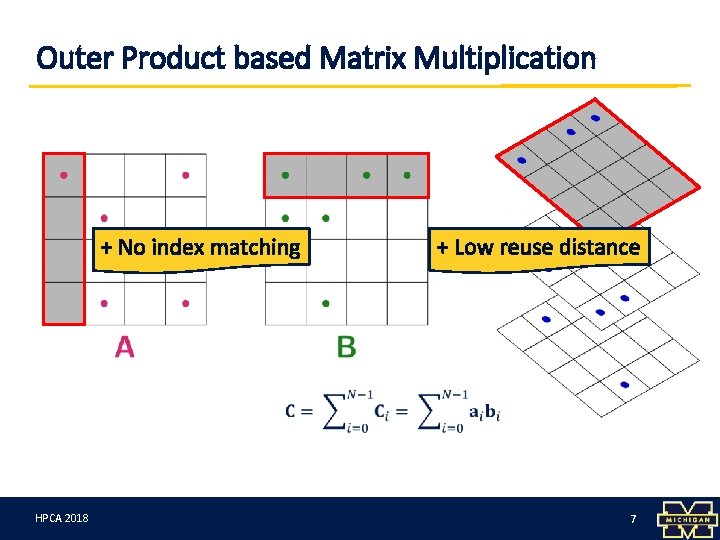
Outer Product based Matrix Multiplication + No index matching HPCA 3/12/18 2018 + Low reuse distance 7 7

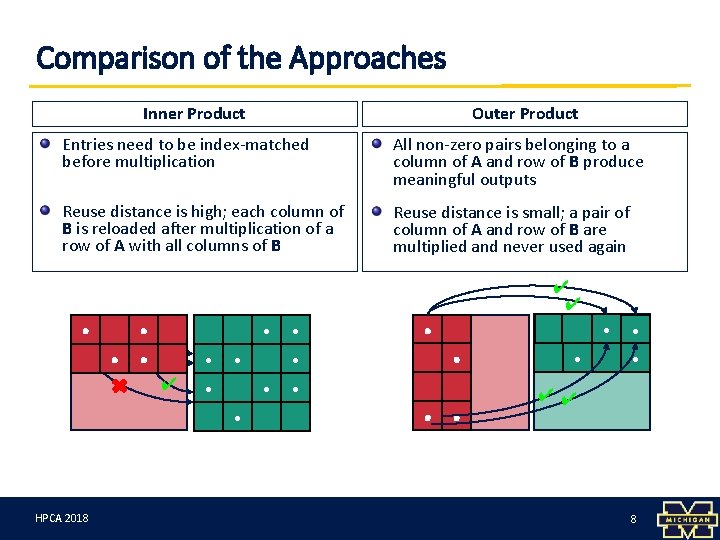
Comparison of the Approaches Inner Product Outer Product Entries need to be index-matched before multiplication All non-zero pairs belonging to a column of A and row of B produce meaningful outputs Reuse distance is high; each column of B is reloaded after multiplication of a row of A with all columns of B Reuse distance is small; a pair of column of A and row of B are multiplied and never used again ∙ HPCA 3/12/18 2018 ∙ ∙ ∙✔ ∙ ∙ ∙ ∙ ✔✔ 8 8

Overview Introduction Algorithm Architecture Evaluation Conclusion HPCA 3/12/18 2018 9 9

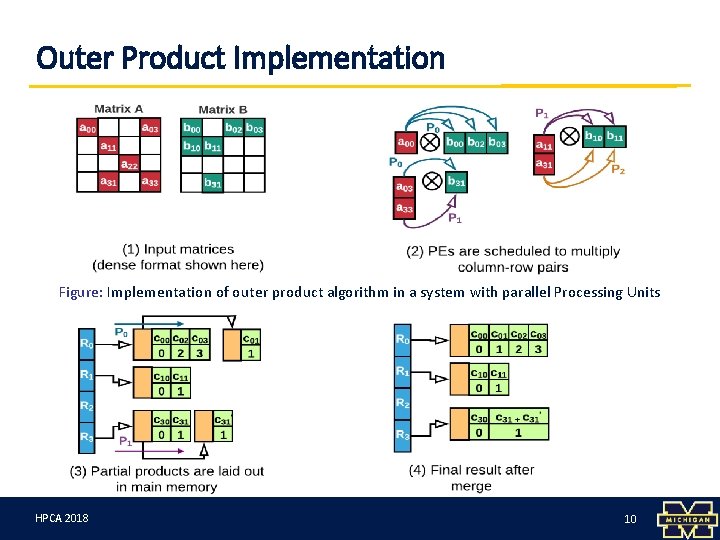
Outer Product Implementation Figure: Implementation of outer product algorithm in a system with parallel Processing Units HPCA 3/12/18 2018 10 10

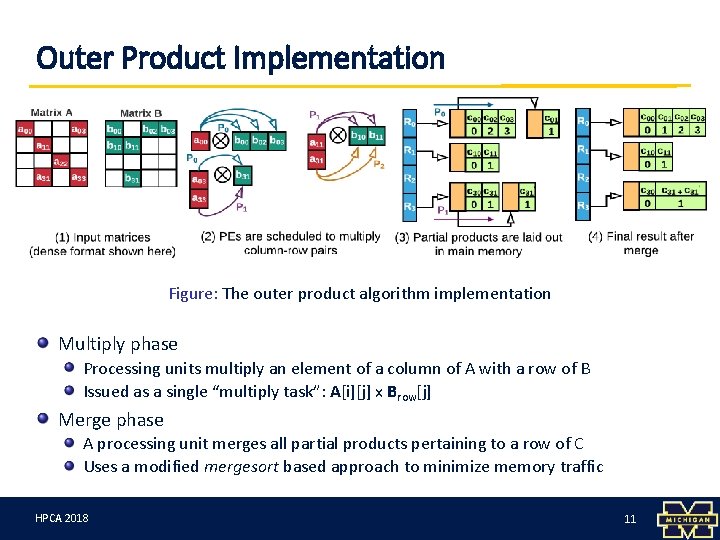
Outer Product Implementation Figure: The outer product algorithm implementation Multiply phase Processing units multiply an element of a column of A with a row of B Issued as a single “multiply task”: A[i][j] x Brow[j] Merge phase A processing unit merges all partial products pertaining to a row of C Uses a modified mergesort based approach to minimize memory traffic HPCA 3/12/18 2018 11 11

Performance on Traditional Hardware: CPU Each matrix has 1 million uniformly distributed non-zeros Matrix dimension Figure: Performance of the outer product algorithm against Intel MKL on the CPU. Evaluated outer product against MKL on Broadwell CPU The outer product algorithm puts high pressure on the memory system N N×N matrices streamed out to main memory during multiply Loaded back in during merge Merge phase implementation involves no sharing, leading to cache thrashing HPCA 3/12/18 2018 12 12

Performance on Traditional Hardware: CPU Each matrix has 1 million uniformly distributed non-zeros Performance bottlenecked Matrix dimension by the restricted cache hierarchy parallelism Figure: Performance of the outerand productcompute algorithm against Intel MKL on the CPU. Evaluated outer product against MKL on Broadwell CPU The outer product algorithm puts high pressure on the memory system N N×N matrices streamed out to main memory during multiply Loaded back in during merge Merge phase implementation involves no sharing, leading to cache thrashing HPCA 3/12/18 2018 13 13

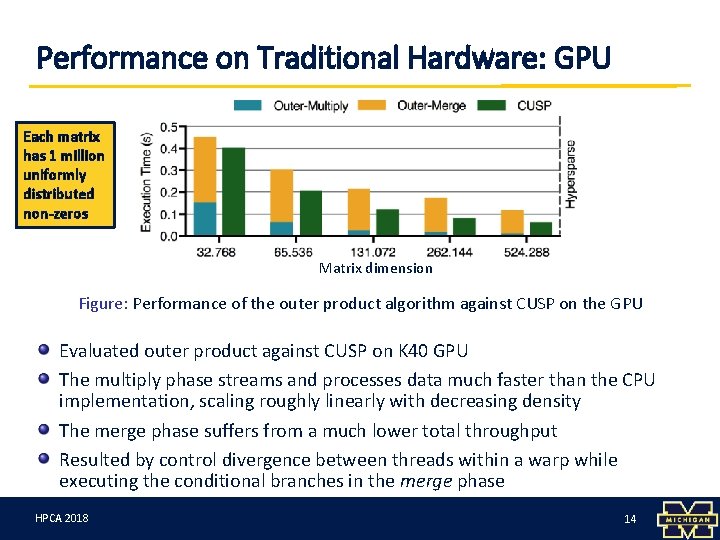
Performance on Traditional Hardware: GPU Each matrix has 1 million uniformly distributed non-zeros Matrix dimension Figure: Performance of the outer product algorithm against CUSP on the GPU Evaluated outer product against CUSP on K 40 GPU The multiply phase streams and processes data much faster than the CPU implementation, scaling roughly linearly with decreasing density The merge phase suffers from a much lower total throughput Resulted by control divergence between threads within a warp while executing the conditional branches in the merge phase HPCA 3/12/18 2018 14 14

Performance on Traditional Hardware: GPU Each matrix has 1 million uniformly distributed non-zeros Performance bottlenecked by the SIMD Matrix dimension Figure: Performance of the outer product algorithm against CUSP on the GPU. Matrices nature of warps Evaluated outer product against CUSP on K 40 GPU The multiply phase streams and processes data much faster than the CPU implementation, scaling roughly linearly with decreasing density The merge phase suffers from a much lower total throughput Resulted by control divergence between threads within a warp while executing the conditional branches in the merge phase Solution: SPMD architecture! HPCA 3/12/18 2018 15 15

Overview Introduction Algorithm Architecture Evaluation Conclusion HPCA 3/12/18 2018 16 16

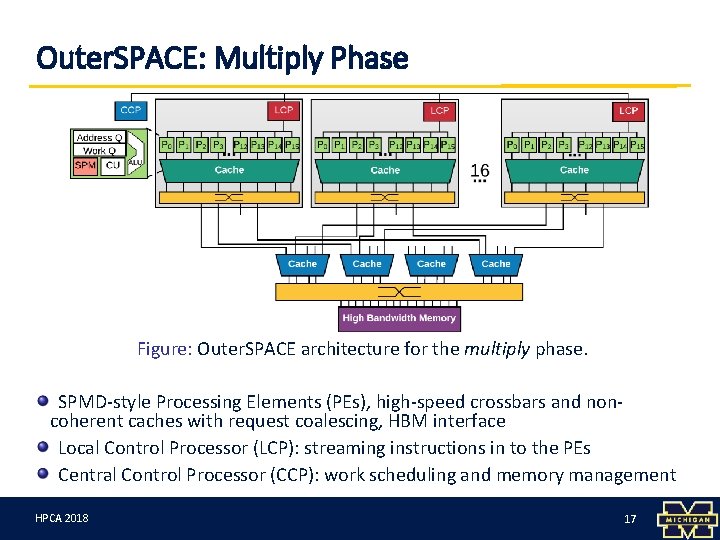
Outer. SPACE: Multiply Phase Figure: Outer. SPACE architecture for the multiply phase. SPMD-style Processing Elements (PEs), high-speed crossbars and noncoherent caches with request coalescing, HBM interface Local Control Processor (LCP): streaming instructions in to the PEs Central Control Processor (CCP): work scheduling and memory management HPCA 3/12/18 2018 17 17

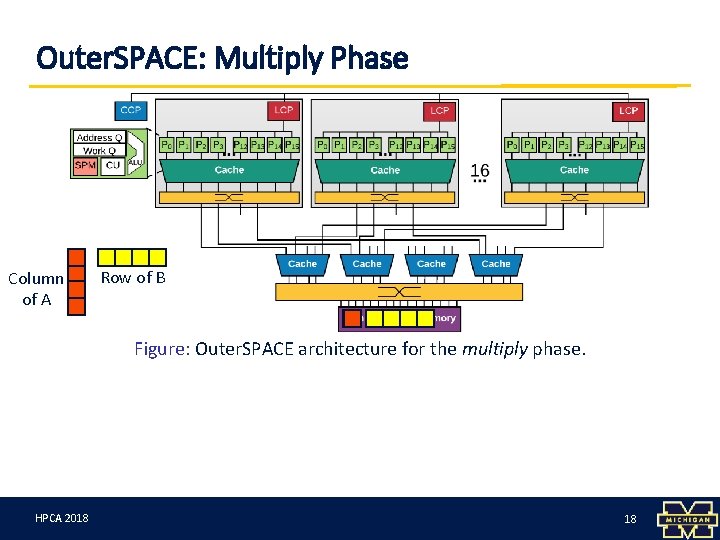
Outer. SPACE: Multiply Phase Column of A Row of B Figure: Outer. SPACE architecture for the multiply phase. HPCA 3/12/18 2018 18 18

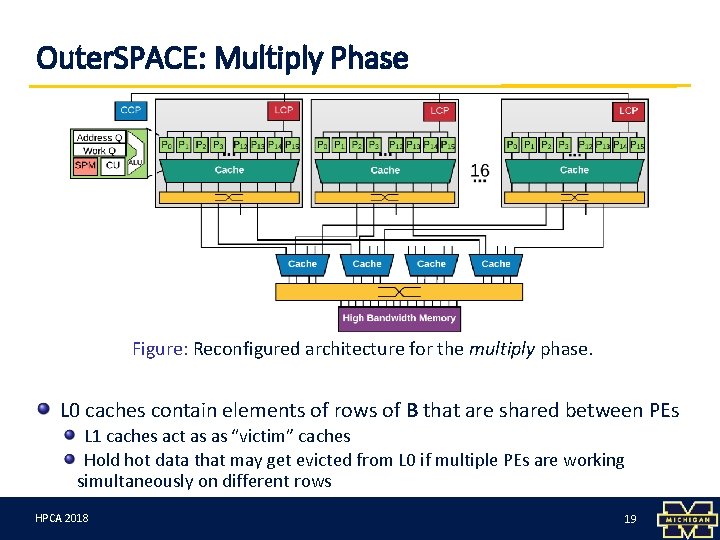
Outer. SPACE: Multiply Phase Figure: Reconfigured architecture for the multiply phase. L 0 caches contain elements of rows of B that are shared between PEs L 1 caches act as as “victim” caches Hold hot data that may get evicted from L 0 if multiple PEs are working simultaneously on different rows HPCA 3/12/18 2018 19 19

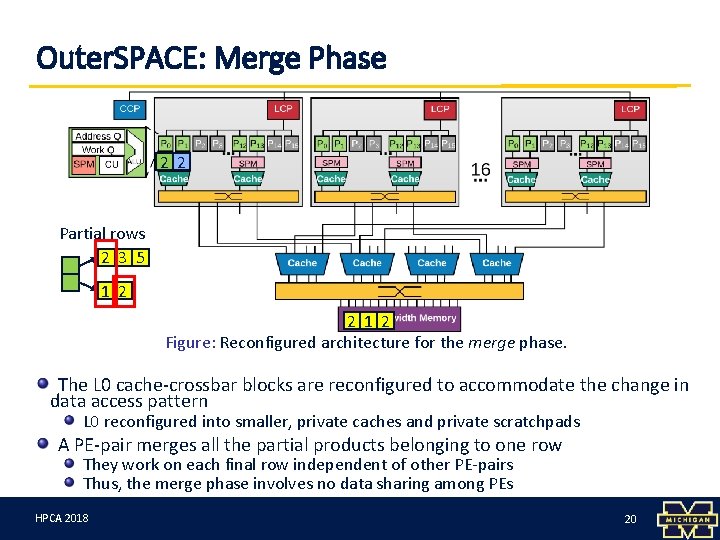
Outer. SPACE: Merge Phase 1 2 2 Partial rows 2 3 5 1 2 2 1 2 Figure: Reconfigured architecture for the merge phase. The L 0 cache-crossbar blocks are reconfigured to accommodate the change in data access pattern L 0 reconfigured into smaller, private caches and private scratchpads A PE-pair merges all the partial products belonging to one row They work on each final row independent of other PE-pairs Thus, the merge phase involves no data sharing among PEs HPCA 3/12/18 20 20

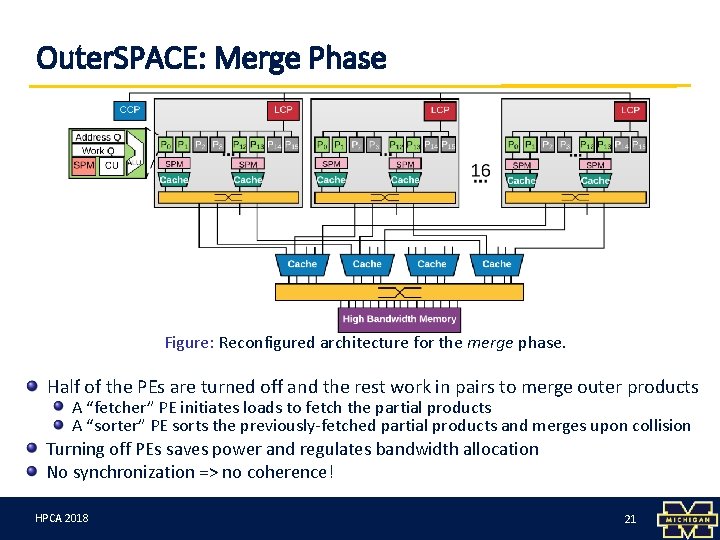
Outer. SPACE: Merge Phase Figure: Reconfigured architecture for the merge phase. Half of the PEs are turned off and the rest work in pairs to merge outer products A “fetcher” PE initiates loads to fetch the partial products A “sorter” PE sorts the previously-fetched partial products and merges upon collision Turning off PEs saves power and regulates bandwidth allocation No synchronization => no coherence! HPCA 3/12/18 2018 21 21

Overview Introduction Algorithm Architecture Evaluation Conclusion HPCA 3/12/18 2018 22 22

Simulation Methodology Modeled the PEs, cachecrossbar hierarchy and HBM using gem 5 Trace-based simulation Generated memory instruction traces offline Fed them to the PEs in the simulator Processing Element (PE) 1. 5 GHz, 64 -entry request. Q 16 PEs/tile for multiply 8 PEs/tile for merge L 0 cache/scratc hpad (SPM) 16 k. B, 4 -way per tile for multiply 2 k. B cache, 2 k. B SPM per tile for merge L 1 cache 4 k. B, 2 -way Crossbar 16 x 16 and 4 x 4, swizzle-switch based Main memory HBM 2. 0, 8000 MB/s per channel, 16 channels Table: gem 5 simulation parameters Evaluated against state-of-the-art Sp. GEMM packages Intel MKL on 6 -core Intel Broadwell CPU NVIDIA cu. SPARSE & CUSP on K 40 GPU HPCA 3/12/18 2018 23 23

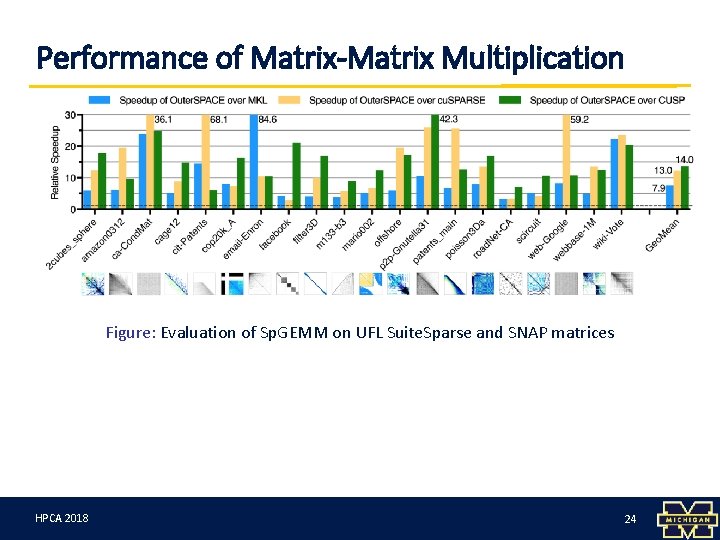
Performance of Matrix-Matrix Multiplication Figure: Evaluation of Sp. GEMM on UFL Suite. Sparse and SNAP matrices HPCA 3/12/18 2018 24 24

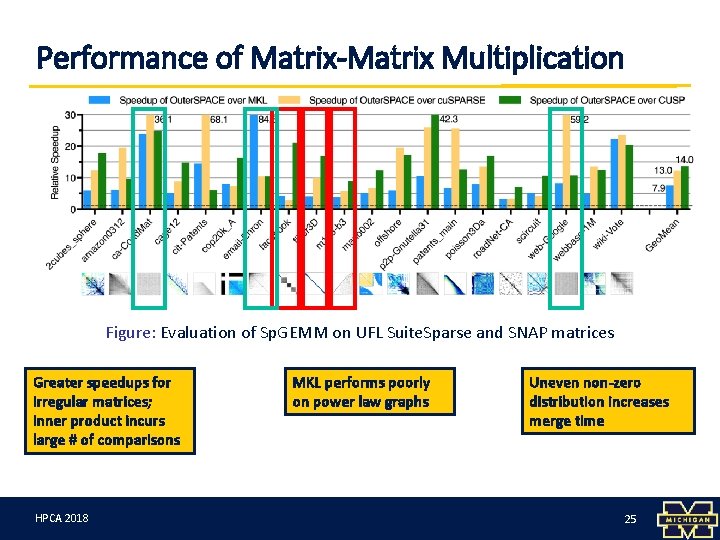
Performance of Matrix-Matrix Multiplication Figure: Evaluation of Sp. GEMM on UFL Suite. Sparse and SNAP matrices Greater speedups for irregular matrices; inner product incurs large # of comparisons HPCA 3/12/18 2018 MKL performs poorly on power law graphs Uneven non-zero distribution increases merge time 25 25

(ms) Performance of Matrix-Vector Multiplication Matrix dimension Figure: Speedups for multiplication with vector of varying density (r) Figure: Performance scaling for multiplication with a dense vector ∼ 10 x gain in speedup with 10 x reduction in vector density for Sp. M-Sp. V multiplication Each matrix has 1 million uniformly distributed nonzeros The outer product method only accesses matrix columns that match the indices of the non-zero elements of the vector Eliminates all redundant accesses to the matrix The outer product algorithm scales with number of non-zeros and not with the density/dimensions of the matrix HPCA 3/12/18 2018 26 26

Power and Area Table: Power and area estimates for Outer. SPACE in 32 nm Total chip area for Outer. SPACE: ∼ 87 mm 2 @ 24 W power budget Average throughput of 2. 9 GFLOPS 126 MFLOPS/W GPU achieves avg. 67 MFLOPS @ 85 W for UFL/SNAP matrices HPCA 3/12/18 2018 27 27

Overview Introduction Algorithm Architecture Evaluation Conclusion HPCA 3/12/18 2018 28 28

Summary Explored the outer product approach for Sp. GEMM Discovered inefficiencies in existing hardware leading to sub-optimal performance Designed a custom architecture following an SPMD paradigm that reconfigures to support different data access patterns Our architecture minimizes memory accesses though efficient use of the cache-crossbar hierarchy Demonstrated acceleration of Sp. GEMM, a prominent memory-bound kernel Evaluated the outer product algorithm on artificial and real-world workloads Outer. SPACE achieves speedups of 7. 9 -14. 0 x over commercial Sp. GEMM libraries on CPU and GPU HPCA 3/12/18 2018 29 29

Questions? HPCA 3/12/18 2018 30 30