Ottimizzazione non lineare non vincolata Metodi iterativi di

Ottimizzazione non lineare non vincolata: Metodi iterativi di eliminazione ed interpolazione per ottimizzazione di funzione di una variabile 10 marzo 2010 MOSPE 1

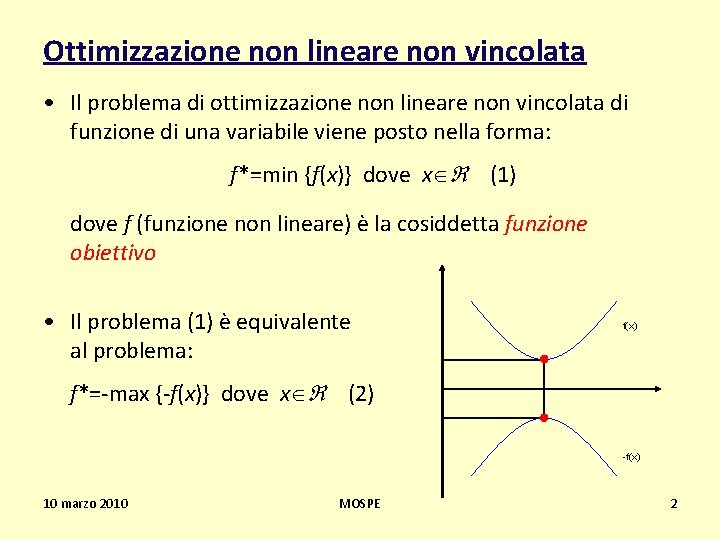
Ottimizzazione non lineare non vincolata • Il problema di ottimizzazione non lineare non vincolata di funzione di una variabile viene posto nella forma: f*=min {f(x)} dove x (1) dove f (funzione non lineare) è la cosiddetta funzione obiettivo • Il problema (1) è equivalente al problema: f(x) f*=-max {-f(x)} dove x (2) -f(x) 10 marzo 2010 MOSPE 2

Metodi iterativi di discesa • La ricerca di una soluzione ottimale per un problema di ottimizzazione non lineare viene condotta utilizzando algoritmi iterativi di discesa • Si tratta di metodi iterativi che percorrono una traiettoria composta da una successione di soluzioni ammissibili, effettuando ad ogni iterazione uno spostamento lungo una direzione ammissibile, in modo che il valore della funzione obiettivo per la nuova soluzione sia inferiore al valore per la soluzione precedente • L’efficienza di un metodo di ricerca consiste nell’ottenere una prescelta approssimazione del punto di minimo con il minor numero possibile di tentativi 10 marzo 2010 MOSPE 3

Classificazione di metodi iterativi Metodi di eliminazione: • Ricerca illimitata • Ricerca esaustiva • Metodo di bisezione (dicotomico) • Metodo di Fibonacci • Metodo della sezione aurea Metodi di interpolazione: • Quadratica • Cubica • Ricerca diretta di radici: – Newton – quasi-Newton – del gradiente • I metodi di eliminazione possono essere usati anche per ottimizzazione di funzioni discontinue e non differenziabili in quanto non utilizzano la derivata della funzione obiettivo!!! 10 marzo 2010 MOSPE 4

Funzione unimodale • I metodi di bisezione, di Fibonacci e della sezione aurea richiedono che la funzione da minimizzare sia unimodale o sia dotata di un unico punto di minimo, su un intervallo chiuso [a, b] • La funzione [a, b] x f(x) si definisce unimodale se x 1<x 2<x* f(x 2)<f(x 1) e x 2>x 1>x* f(x 1)<f(x 2) dove x* è il punto minimo della funzione. • In altre parole - esiste un valore x* [a, b] tale che la funzione è strettamente decrescente per x<x* e strettamente crescente per x*>x - o viceversa 10 marzo 2010 MOSPE 5

Funzione unimodale vs funzione multimodale 10 marzo 2010 MOSPE 6

Ricerca illimitata • Un metodo elementare di ricerca del punto ottimale della funzione f è basato sull’uso di passo fisso e spostamento, da un punto iniziale scelto, nella direzione favorevole (positiva o negativa). Il passo usato deve essere piccolo in relazione con l’accuratezza finale desiderata • Nella ricerca illimitata (ed in tutti gli altri metodi di eliminazione) si assume che la funzione f sia unimodale. Nel caso di funzione multimodale l’intervallo di esplorazione per la funzione viene suddiviso in diverse parti in ciascuna della quali la funzione è unimodale. 10 marzo 2010 MOSPE 7

Esempio di ricerca non limitata con passo fisso 10 marzo 2010 MOSPE 8

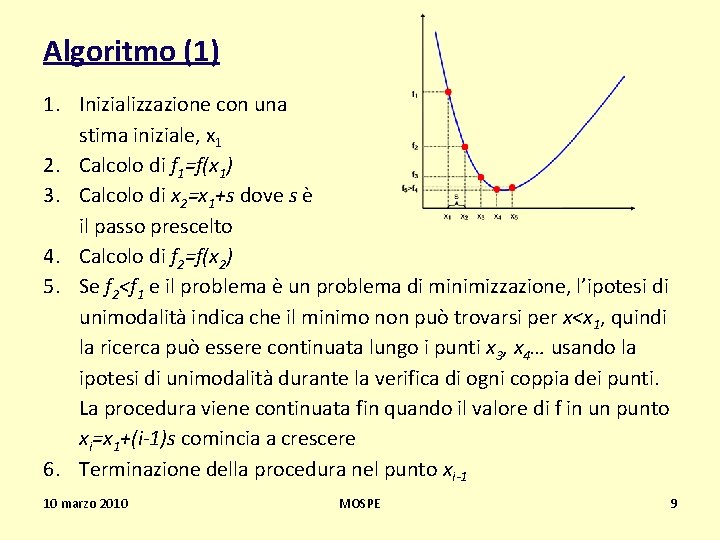
Algoritmo (1) 1. Inizializzazione con una stima iniziale, x 1 2. Calcolo di f 1=f(x 1) 3. Calcolo di x 2=x 1+s dove s è il passo prescelto 4. Calcolo di f 2=f(x 2) 5. Se f 2<f 1 e il problema è un problema di minimizzazione, l’ipotesi di unimodalità indica che il minimo non può trovarsi per x<x 1, quindi la ricerca può essere continuata lungo i punti x 3, x 4… usando la ipotesi di unimodalità durante la verifica di ogni coppia dei punti. La procedura viene continuata fin quando il valore di f in un punto xi=x 1+(i-1)s comincia a crescere 6. Terminazione della procedura nel punto xi-1 10 marzo 2010 MOSPE 9

Algoritmo (1) 7. Se all’inizio f 2>f 1 la ricerca deve essere svolta nella direzione opposta cioè per i punti x-2, x-3…, dove x-j=x 1 -(j-1)s 8. Se f 2=f 1 il minimo cercato sta tra x 2 e x 1 e quindi il punto di minimo può essere scelto sia in x 2 sia in x 1 9. Se sia f 2 sia f-2 sono più grandi di f 1, questo implica che il minimo si trova nell’intervallo x-2<x<x 2 10 marzo 2010 MOSPE 10

Passo accelerato • Anche se la ricerca con passo fisso sembra molto semplice, la maggiore limitazione viene dal fatto della natura non limitata del regione dove si può trovare il minimo • Per esempio se il punto minimo di una certa funzione f si trova a x*=50000 e, in assenza di conoscenza della sua posizione, x 1 ed s vengono scelti come 0 e 0. 1, la funzione f deve essere valutata 50001 volte per trovare il minimo! • Per risolvere questo problema, per esempio, in ogni iterazione il passo può essere raddoppiato. Successivamente, per ottenere una sufficiente accuratezza, la procedura di base può essere applicata all’intervallo (xi-1, xi) cominciando da xi-1 o xi 10 marzo 2010 MOSPE 11

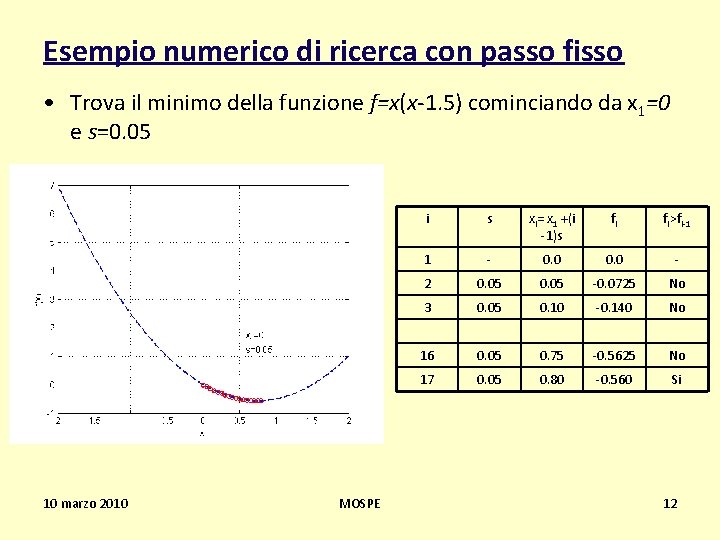
Esempio numerico di ricerca con passo fisso • Trova il minimo della funzione f=x(x-1. 5) cominciando da x 1=0 e s=0. 05 10 marzo 2010 MOSPE i s xi= x 1 +(i -1)s fi fi>fi-1 1 - 0. 0 - 2 0. 05 -0. 0725 No 3 0. 05 0. 10 -0. 140 No 16 0. 05 0. 75 -0. 5625 No 17 0. 05 0. 80 -0. 560 Si 12

Esempio numerico di ricerca con passo accel. • Trova il minimo della funzione f=x(x-1. 5) cominciando da x 1=0 e s=0. 05 10 marzo 2010 MOSPE i s xi= x 1 +s fi fi>fi-1 1 - 0. 0 - 2 0. 05 -0. 0725 No 3 0. 10 -0. 140 No 4 0. 20 -0. 260 No 5 0. 40 -0. 440 No 6 0. 80 -0. 560 No 7 1. 60 +0. 160 Si 13

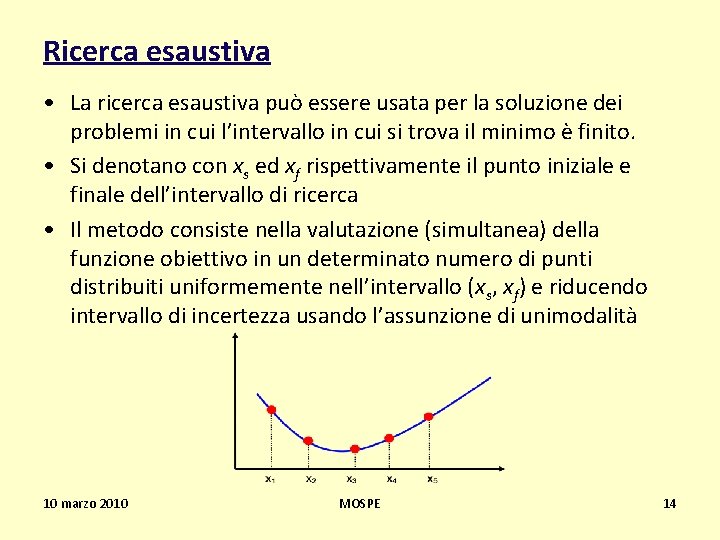
Ricerca esaustiva • La ricerca esaustiva può essere usata per la soluzione dei problemi in cui l’intervallo in cui si trova il minimo è finito. • Si denotano con xs ed xf rispettivamente il punto iniziale e finale dell’intervallo di ricerca • Il metodo consiste nella valutazione (simultanea) della funzione obiettivo in un determinato numero di punti distribuiti uniformemente nell’intervallo (xs, xf) e riducendo intervallo di incertezza usando l’assunzione di unimodalità 10 marzo 2010 MOSPE 14

Metodo di bisezione (dicotomico) • Nel metodo di bisezione esattamente la metà dell’intervallo corrente viene scartata in ogni iterazione • Il metodo richiede tre punti iniziali e due punti sperimentali in ogni iterazione della procedura 10 marzo 2010 MOSPE 15

Algoritmo 1. Suddivisione dell’intervallo di incertezza L 0=[a, b] in 4 parti uguali, con x 0 al centro 2. Valutazione della funzione obiettivo f nei punti x 0, x 1 , x 2 3. Se: a) f(x 2)>f(x 0)>f(x 1) cancella [x 0, b] e sostituisci x 0 = x 1 e b=x 0 b) f(x 2)<f(x 0)<f(x 1) cancella [a, x 0] e sostituisci x 0 =x 2 e a=x 0 c) f(x 1)>f(x 0) e f(x 2)> f(x 0) cancella [a, x 1] e [x 2, b] e sostituisci a=x 1 e b=x 2 4. Controlla se il nuovo intervallo L=b-a soddisfa il criterio di convergenza L<=epsilon; se converge finisci la procedura se no torna al punto 1 10 marzo 2010 MOSPE 16

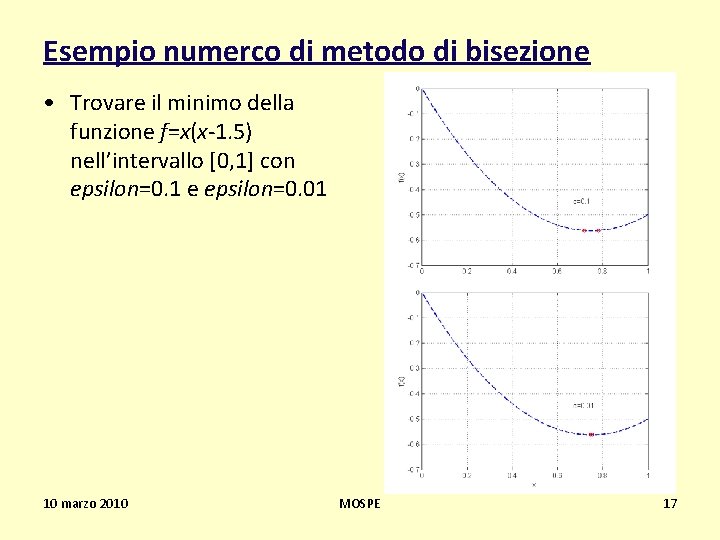
Esempio numerco di metodo di bisezione • Trovare il minimo della funzione f=x(x-1. 5) nell’intervallo [0, 1] con epsilon=0. 1 e epsilon=0. 01 10 marzo 2010 MOSPE 17

Metodo di Fibonacci • Il metodo di Fibonacci può essere applicato per la ricerca del minimo di una funzione di una variabile anche non continua. • Come tanti altri metodi di eliminazione esistono le seguenti limitazioni per quanto riguarda l’uso del metodo: – L’intervallo iniziale di incertezza deve essere noto – La funzione obiettivo deve essere unimodale in questo intervallo – La soluzione esatta non può essere trovata – solo un intervallo finale di incertezza – Il numero di valutazioni della funzione o la risoluzione deve essere specificato all’inizio della procedura 10 marzo 2010 MOSPE 18

Numeri di Fibonacci • Il metodo usa la sequenza di numeri di Fibonacci Fn , definiti tramite la relazione ricorsiva: F 0=F 1=1 Fn=Fn-1+Fn-2 n=2, 3, 4, … che determina la successione: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, … • L’algoritmo si basa sulla valutazione della funzione obiettivo f in corrispondenza di una successione finita di n punti, e ricava un intervallo di incertezza, di ampiezza decrescente con n, all’interno del quale si colloca la soluzione ottimale. 10 marzo 2010 MOSPE 19

Algoritmo (1) 1. 2. Inizializzazione con due punti di tentativo x 1 e x 2 posti a distanza L 2*=Fn 2/Fn·L 0 dagli estremi dell’intervallo L 0=[a, b] dove n è il numero totale di valutazioni: x 1=a+ L 2*=a+ Fn-2/Fn·L 0 x 2=b-L 2*=b- Fn-2/Fn·L 0 =a+ Fn-1/Fn·L 0 (se un punto è posto alla distanza Fn-2/Fn·L 0 da un estremo dell’intervallo, sarà posto alla distanza Fn-1/Fn·L 0 dall’altro estremo) Sulla base di assunzione di unimodalità una parte dell’intervallo viene scartata; il rimanente intervallo di incertezza ha lunghezza L 2 definita: L 2=L 0 -L 2*=L 0(1 -Fn-2/Fn)= Fn-1/Fn·L 0 e contiene uno dei punti di tentativo alla distanza: L 2*= Fn-2/Fn·L 0= Fn-2/Fn-1·L 2 da un lato e L 2 -L 2*= Fn-3/Fn·L 0= Fn-3/Fn-1·L 2 dall’altro lato dell’intervallo L 2 10 marzo 2010 MOSPE 20

Algoritmo (2) 3. 4. 5. 6. 7. Si procede con il terzo tentativo x 3 nell’intervallo L 2 alla distanza: L 3*= Fn-3/Fn·L 0= Fn-3/Fn-1·L 2 da ogni lato dell’ intervallo L 2 Usando la condizione di unimodalità l’intervallo di incertezza viene ridotto all’intervallo L 3: L 3=L 2 -L 3*=L 2 - Fn-3/Fn-1·L 2= Fn-2/Fn-1·L 2 = Fn-2/Fn·L 0 Il processo viene continuato con: Lj*= Fn-j/Fn-(j-2)·Lj-1 Lj = Fn-(j-1)/Fn·L 0 Dopo un numero di passi uguale a j il rapporto tra l’intervallo determinato e quello residuo è uguale a: Lj /L 0 = Fn-(j-1)/Fn Per j=n abbiamo: Ln /L 0 = F 1/Fn =1/Fn 10 marzo 2010 MOSPE 21

Esempio numerico di metodo di Fibonacci • Trova un minimo di f(x)=0. 65[0. 75/(1+x 2)]-0. 65 xtan-1(1/x) su intervallo [0, 3] usando n=6 • • n=6, L 0=3 L 2*=Fn-2/Fn·L 0=5/13· 3=1. 153846 x 1=1. 153846 f(x 1)=-0. 207270 x 2=3 -1. 153846=1. 846154 f(x 2)=-0. 115843 f(x 1)<f(x 2) [x 2, 3] viene scartato x 3=0+(x 2 -x 1)=0. 692308 f(x 3)=-0. 291364 f(x 1)>f(x 3) [x 1, x 2] viene scartato (…. . ) 10 marzo 2010 MOSPE L 0 L 2 * L 2 x 2 L 2 * x 1 x 3 22

Metodo della sezione aurea • Il metodo della sezione aurea è simile al metodo di Fibonacci eccetto che nel metodo di Fibonacci il numero totale di tentativi viene specificato all’inizio per determinare la posizione iniziale dei punti; nel metodo della sezione aurea si assume che il numero di tentativi sia molto grande (n ∞) • È possibile dimostrare che con n ∞ abbiamo: limn ∞Fn-1/Fn=1/π1 0. 618 dove π1 1. 618 è una radice dell’equazione x 2=x+1 e costituisce la sezione aurea, già nota nell’antica Grecia • Nel metodo i punti iniziali x 1 e x 2 vengono scelti in corrispondenza di: L 2*=Fn-2/Fn·L 0 =Fn-2/Fn-1·Fn-1/Fn·L 0=L 0/π12=0. 382 L 0 10 marzo 2010 MOSPE 23

Sezione aurea • La sezione aurea, nell'ambito dell‘arte e della matematica, indica il rapporto fra due grandezze disuguali, delle quali la maggiore è medio proporzionale tra la minore e la somma delle due, mentre lo stesso rapporto esiste anche tra la grandezza minore e la loro differenza. • In formule, indicando con a la lunghezza maggiore e con b la lunghezza minore, vale la relazione: (a+b) : a = a : b = b : (a-b) 10 marzo 2010 MOSPE 24

Arco di Traiano e sezione aurea 10 marzo 2010 MOSPE 25

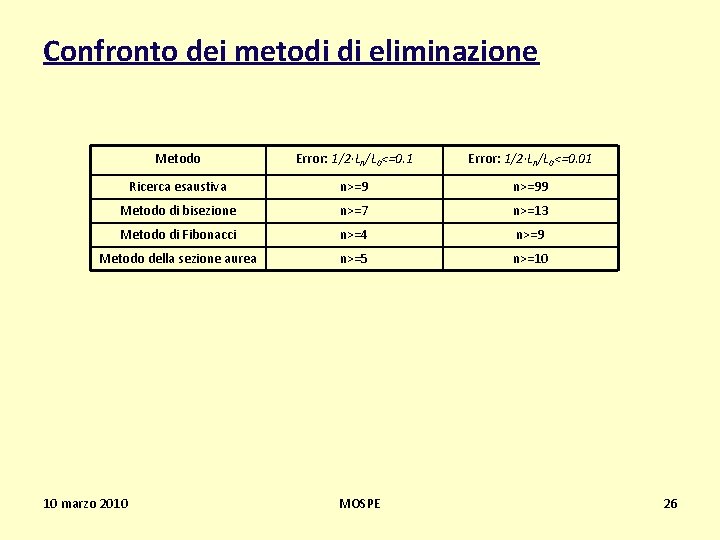
Confronto dei metodi di eliminazione Metodo Error: 1/2·Ln/L 0<=0. 1 Error: 1/2·Ln/L 0<=0. 01 Ricerca esaustiva n>=99 Metodo di bisezione n>=7 n>=13 Metodo di Fibonacci n>=4 n>=9 Metodo della sezione aurea n>=5 n>=10 10 marzo 2010 MOSPE 26

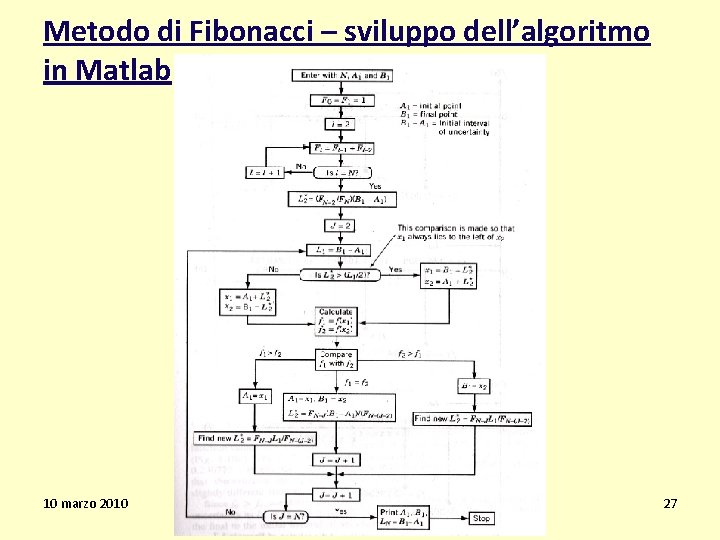
Metodo di Fibonacci – sviluppo dell’algoritmo in Matlab 10 marzo 2010 MOSPE 27

Ricerca diretta di radici • Metodo di Newton • Metodo quasi Newtoniano • Metodo della secante 10 marzo 2010 MOSPE 28

Convergenza (1) • Convergenza (def. 1): La sequenza xi delle iterazioni converge alla soluzione α se: • Convergenza (def. 2): La sequenza xi delle iterazioni converge alla soluzione α se, dato un ε>0 qualsiasi, esiste un intero n 0 tale per cui con n≥n 0 si ha: • Convergenza lineare: La sequenza xi delle iterazioni converge linearmente alla soluzione α se esiste una costante c con 0<c<1 ed un intero n≥ 0 tali per cui: 10 marzo 2010 MOSPE 29

Convergenza (2) • Convergenza superlineare: La sequenza xi delle iterazioni converge superlinearmente alla soluzione α se, per qualche sequenza cn che converge a 0, esiste un intero n≥ 0 tali per cui: • Convergenza di ordine p: La sequenza xi delle iterazioni converge con ordine p ≥ 1 alla soluzione α se, per qualche c>0, esiste un intero n ≥ 0 tale per cui: p è anche detto ordine di convergenza del metodo. 10 marzo 2010 MOSPE 30