Otimizao do mtodo multigrid geomtrico para sistemas de

Otimização do método multigrid geométrico para sistemas de equações 2 D em CFD Doutorando: Cosmo D. Santiago – MSc. Orientador: Carlos H. Marchi – Dr. Eng. Projeto Multigrid - IAE/CTA –maio/2008 Programa de Pós-Graduação em Engenharia Mecânica -PG-Mec - UFPR

Objetivos dessa apresentação ü Apresentar um resumo de resultados já obtidos. ü Atividades em andamento ü Resultados esperados

Objetivos dessa etapa da pesquisa ü Obter parâmetros ótimos do método multigrid geométrico para 2 sistemas de equações. Os parâmetros estudados são: - Iterações internas (ITI); - Número de níveis (L); - Influência do número de variáveis (N). ü Verificar a influência do número de variáveis no multigrid ü Verificar se os valores ótimos obtidos com os 2 sistemas são os mesmos obtidos para uma equação.

Problemas testes ü Equação de Laplace ü Equações de Navier ü Equações Burgers Esquema de comparação Laplace (linear) (CS/FAS) Navier (linear) (FAS) Burgers (não-linear)

Modelos Matemáticos – 2 D • Equação de Laplace A solução analítica é dada por T(x, y) = xy. Com as seguintes condições de contorno:

Modelos Matemáticos – 2 D • Equações de Navier (Termoelasticidade) onde: Cλ = (1+ λ)/(1 - λ) e λ é a razão de Poisson é o campo de temperaturas. α é o coeficiente de expansão térmica u e v são deslocamentos

Modelos Matemáticos – 2 D Solução analítica proposta e Com as seguintes condições de contorno: . e Superior: Inferior: e Direito: Esquerdo: e e

Modelos Matemáticos – 2 D • Equações de Burgers onde : p é a pressão dada por Shih et al. (1989) B é o termo fonte u e v representam as velocidades.

Modelos Matemáticos – 2 D Solução analítica para as velocidades (SHIH et al. , 1989) e As condições de contorno são: Superior: Inferior: Direito: Esquerdo: e

Modelo numérico Para os três problemas: - Discretização com o Método de Diferenças Finitas - Malha uniformes nas duas direções coordenadas - Aproximações: UDS/CDS para os termos advectivos e difusivos, respectivamente - Multigrid Geométrico com ciclo V - Razão de engrossamento padrão (2) - Restrição: Injeção - Prolongação: Interpolação bilinear - Solver padrão: MSI - Condições de contorno de Dirichlet

Implementação § Linguagem: Fortran/95 § Multigrid Geométrico com Ciclo V § Algoritmos: CS e FAS : Equação de Laplace e equações de Navier FAS : Equações de Burgers § Tolerância

Resultados Equação de Laplace x Equações de Navier Iterações internas (ITI) (a) Iterações internas com CS (b) Iterações internas com FAS Fig. 1: Comparação do número de iterações internas com os esquemas CS e FAS Conclusão: ITIoptimum = 2 (para os dois problemas) Conclusão: ITIoptimum = 2 para Navier ITIoptimum = 8 para Laplace

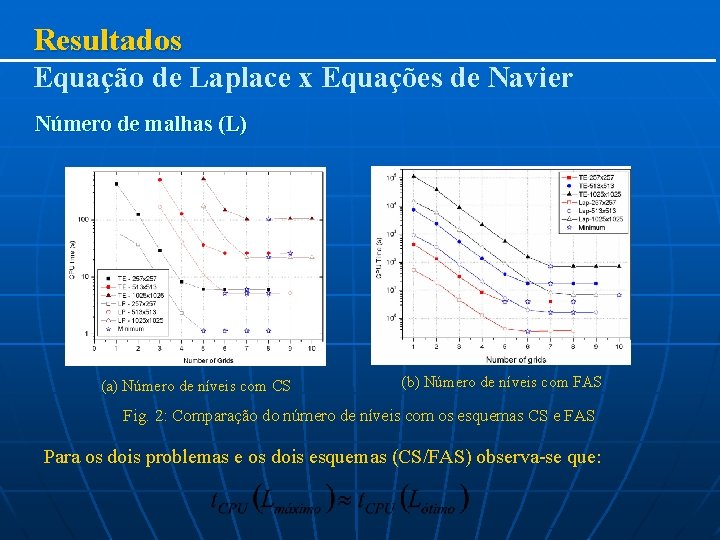
Resultados Equação de Laplace x Equações de Navier Número de malhas (L) (a) Número de níveis com CS (b) Número de níveis com FAS Fig. 2: Comparação do número de níveis com os esquemas CS e FAS Para os dois problemas e os dois esquemas (CS/FAS) observa-se que:

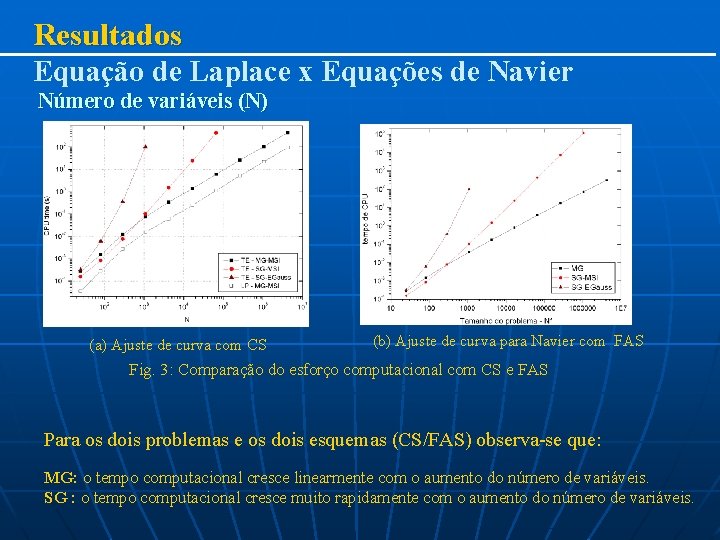
Resultados Equação de Laplace x Equações de Navier Número de variáveis (N) (a) Ajuste de curva com CS (b) Ajuste de curva para Navier com FAS Fig. 3: Comparação do esforço computacional com CS e FAS Para os dois problemas e os dois esquemas (CS/FAS) observa-se que: MG: o tempo computacional cresce linearmente com o aumento do número de variáveis. SG : o tempo computacional cresce muito rapidamente com o aumento do número de variáveis.

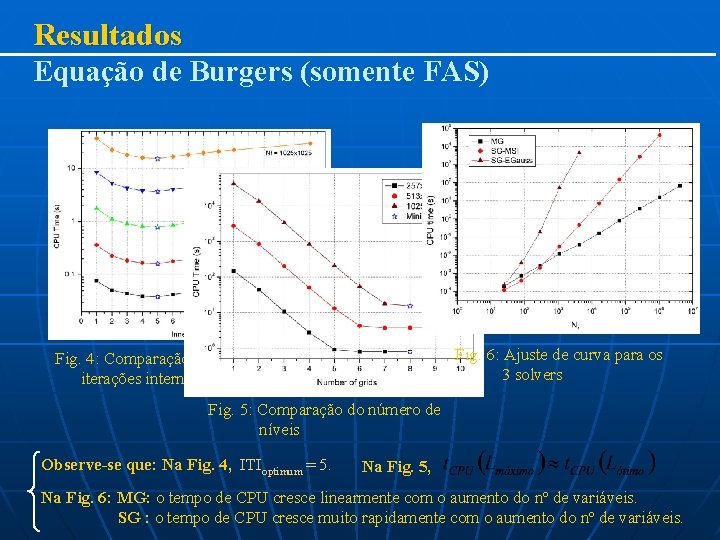
Resultados Equação de Burgers (somente FAS) Fig. 6: Ajuste de curva para os 3 solvers Fig. 4: Comparação do número de iterações internas com o FAS Fig. 5: Comparação do número de níveis Observe-se que: Na Fig. 4, ITIoptimum = 5. Na Fig. 5, Na Fig. 6: MG: o tempo de CPU cresce linearmente com o aumento do nº de variáveis. SG : o tempo de CPU cresce muito rapidamente com o aumento do nº de variáveis.

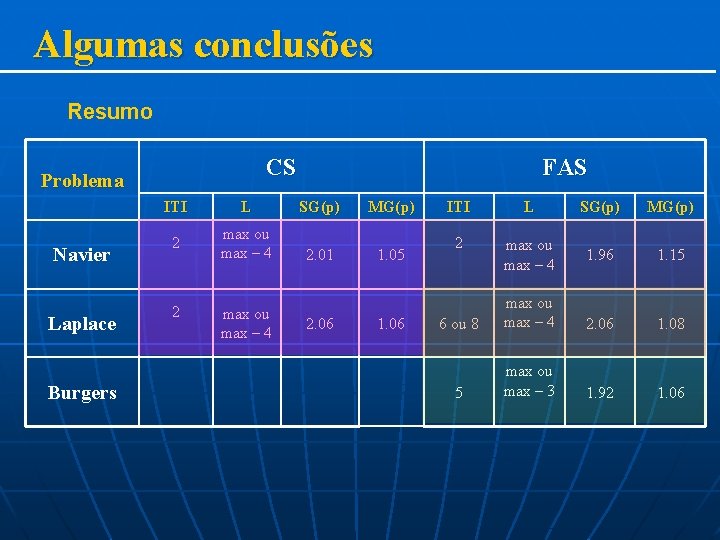
Algumas conclusões Resumo CS Problema Navier Laplace Burgers FAS ITI L SG(p) MG(p) 2 max ou max – 4 2. 01 1. 05 2 max ou max – 4 2. 06 1. 06 ITI L SG(p) MG(p) 2 max ou max – 4 1. 96 1. 15 6 ou 8 max ou max – 4 2. 06 1. 08 5 max ou max – 3 1. 92 1. 06

Algumas conclusões Verificou–se que: Equação de Laplace x Equações de Navier Esquema CS Ø ITIoptimum = 2, em qualquer malha. O ITI afeta significativamente o tempo de CPU. Ø O número ótimo de malhas é próximo do máximo, isto é, Loptimum ≈ Lmaximum. O número de malhas pode afetar significativamente o tempo de CPU Ø O tempo de CPU cresce aproximadamente linear com o aumento do número de variáveis. Ø O acoplamento de duas equações não degenera a perfomance do multigrid quando comparado com o caso de uma equação.

Algumas conclusões Esquema FAS Ø Ø ITIoptimum = 8, (Equação de Laplace) ITIoptimum = 2, (Equações de Navier) O ITI afeta significativamente o tempo de CPU. Ø Nº de níveis (Idem a conclusão com esquema CS). Ø Acoplamento (Idem a conclusão com esquema CS). Ø O tempo de CPU (Idem a conclusão com esquema CS)

Algumas conclusões Equações de Burgers (apenas esquema FAS) Ø ITIoptimum = 5, em todas as malhas. O ITI afeta significativamente o tempo de CPU. Ø Nº de níveis (Idem aos casos anteriores). Ø Acoplamento (Idem aos casos anteriores). Ø O tempo de CPU (Idem aos casos anteriores).

Próximas etapas Otimizar o método multigrid geométrico ciclo V para as equações de Navier-Stokes nas formulações: Ø Função Corrente-Velocidade (mai/jun); Ø Função Corrente-Vorticidade (jul/ago/set); Ø Vorticidade –Velocidade (out/nov/dez); Modelo numérico: Mesmo usado com os problemas mostrado aqui.

Próximas etapas Resultados esperados: Ø Otimizar o método multigrid geométrico ciclo V para problemas com duas equações; Ø Mostrar que o acoplamento das equações não degenera a performance do método multigrid. Ø Obter parâmetros ótimos do multigrid para as equações de Navier-Stokes em formulações alternativas.

Agradecimentos - A Agencia Espacial Brasileira – AEB pelo suporte financeiro Laboratório de Experimentação Numérica (LENA) do Demec/UFPR; Prof. Marchi Meus amigos do LENA.