Other Trees Applications of the Tree Structure Creative

Other Trees Applications of the Tree Structure Creative Commons License – Curt Hill.

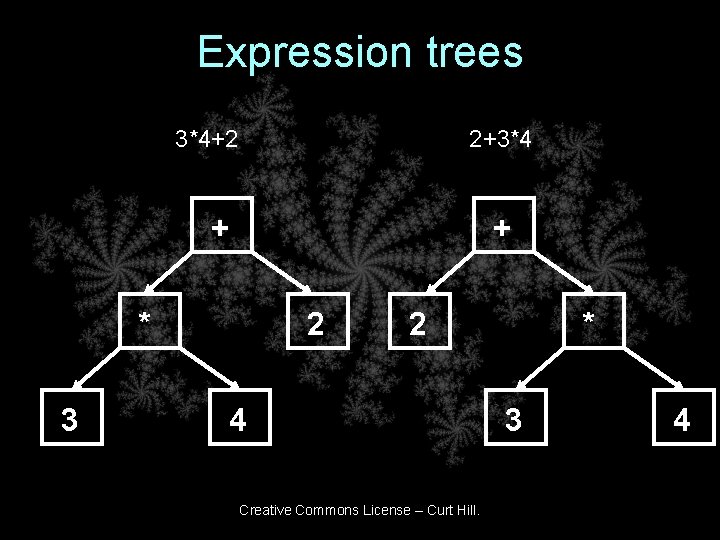
Expression trees • An expression tree contains: – Operators as interior nodes – Values as leaves • The shape of the expression tree captures the precedence • Consider the following expression: 2+3*4 Creative Commons License – Curt Hill.

Expression trees 3*4+2 2+3*4 + + * 3 2 2 4 Creative Commons License – Curt Hill. * 3 4

Traversal • The names come from the above expression tree • There are six (3!) ways to traverse the depending on the order of processing: – The node – The left subtree – The right subtree • Inorder (left and right) • Preorder • Postorder Creative Commons License – Curt Hill.

Inorder • • According to the sorted order of tree Visit lower (left) subtree Process node Visit upper (right) subtree The reverse produces higher to lower Left to right 2 + 3 * 4 This gives standard algebraic notation Creative Commons License – Curt Hill.

Preorder • • • Node first then subtrees Process node Visit lower (left) subtree Visit upper (right) subtree Expression + 2 * 3 4 Remember this? Creative Commons License – Curt Hill.

Postorder • • • Subtrees first and then node Visit lower (left) subtree Visit upper (right) subtree Process node Expression: 2 3 4 * + Reverse Polish Creative Commons License – Curt Hill.

Parse Trees • Expression trees are a small instance of parse trees • A presentation on parse trees also exists Creative Commons License – Curt Hill.

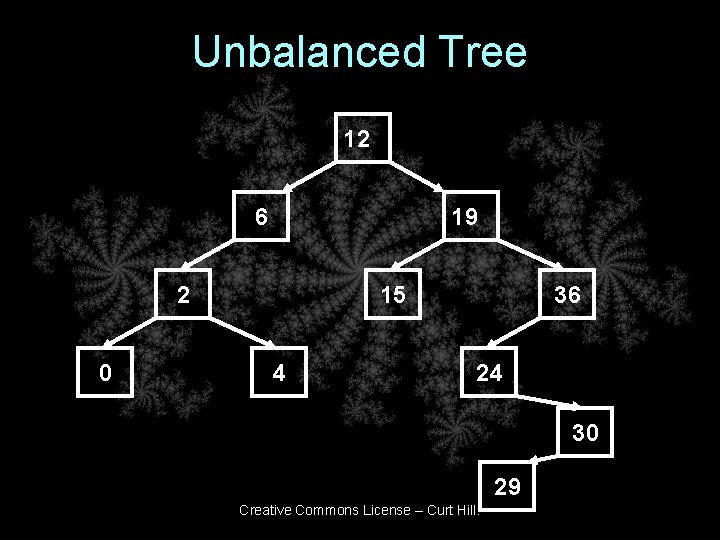
Balance and Search Times • The time it takes to search a tree is based upon the path length to the desired node • Assuming equal distributions then – The average search is the sum of the path lengths divided by the number of tree nodes Creative Commons License – Curt Hill.

Unbalanced Tree 12 6 19 2 0 15 4 36 24 30 29 Creative Commons License – Curt Hill.

Average Search Length • • • 12 – 1 6 – 2 19 – 2 2 – 3 15 – 3 36 – 3 • • • 24 – 4 0 – 4 4 – 4 30 – 5 29 – 6 • Sum of 37 for 11 nodes gives average search length of 3. 3 Creative Commons License – Curt Hill.

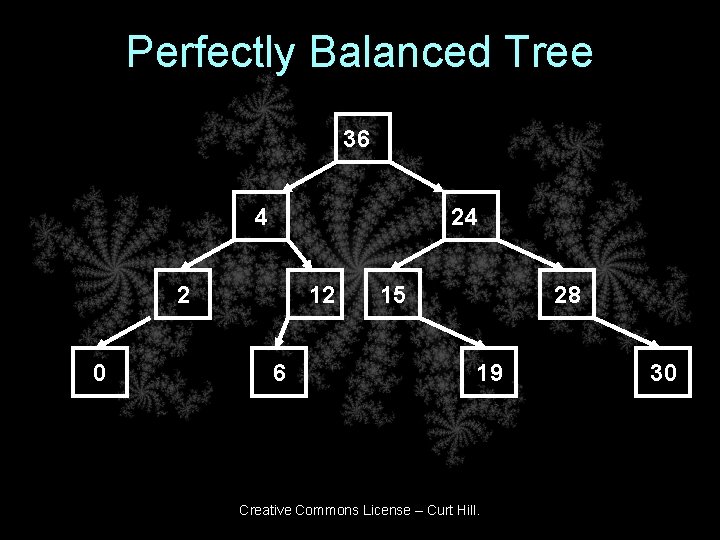
Perfectly Balanced Tree 36 4 24 2 0 12 6 15 28 19 Creative Commons License – Curt Hill. 30

Average Search Length • • 36 – 1 4 – 2 2 – 3 12 - 3 15 – 3 28 – 3 • • 0 – 4 6 – 4 19 – 4 30 – 4 • Sum of 33 for 11 nodes gives average search length of 3. 0 • Balanced does perform better Creative Commons License – Curt Hill.

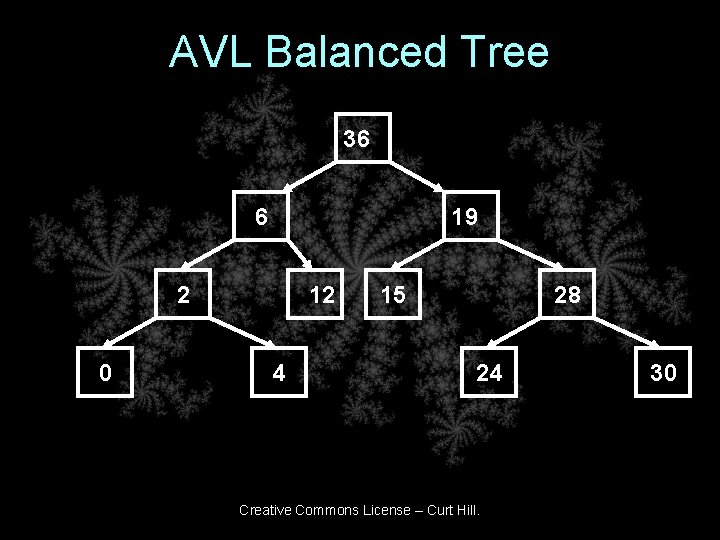
AVL Balanced Tree 36 6 19 2 0 12 4 15 28 24 Creative Commons License – Curt Hill. 30

Average Search Length • • 36 – 1 6 – 2 19 – 2 2 – 3 12 - 3 15 – 3 28 – 3 • • 0 – 4 4 – 4 28 – 4 30 – 4 • Sum of 33 fpr 11 nodes gives average search length of 3. 0 • AVL balanced has the same performance as perfectly balanced Creative Commons License – Curt Hill.

Balanced is Best? • The idea of balancing a tree is predicated on equal frequencies of keys – Reasonable assumption if no contrary information – However, if we have frequency information, we can do better • C++ keywords are not evenly distributed Creative Commons License – Curt Hill.

Path Lengths • The idea of balance is nice in general but… • If we have a reasonable idea of the frequency of entries, we can do better than perfectly balanced • What we want to do is minimize the average path length • With our previous knowledge we could make no assumptions concerning frequency • Now we can generate a more precise formula Creative Commons License – Curt Hill.

Average Path Length • Creative Commons License – Curt Hill.

Optimal Search Trees • What we want are high frequency words close to the root and low frequency words at the leaves • You might think that the most common word should be the root and the next two words the second and third common • It does not work that way since we need to maintain the order as well Creative Commons License – Curt Hill.

Example • For example the word "the" is the most common word in English text • The top n are: – – – – the (20) and (15) of (13) to (12) you (7) in (7) a (6) • Because the top two are such extremes it may be better to have “of” as the root Creative Commons License – Curt Hill.

LISP Lists • LISP is very old – Second only to FORTRAN • Usually encountered in Programming Languages or Artificial Intelligence classes • It has a ubiquitous data structure called a list • However it is not a list in the sense that it is purely linear • Instead it is a tree, but a tree without a Creative Commons License – Curt Hill. key

Variables in LISP • A variable may be: – An atom – A list • An atom is any word or number • A list may be: – Empty – A variable followed by a list Creative Commons License – Curt Hill.

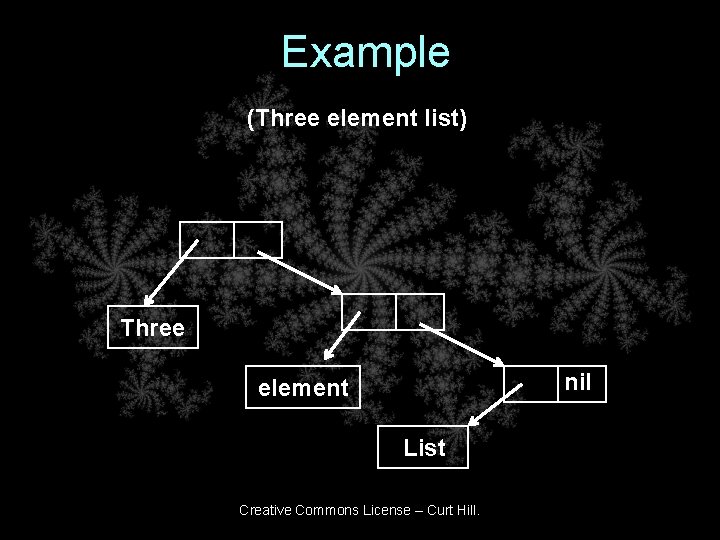
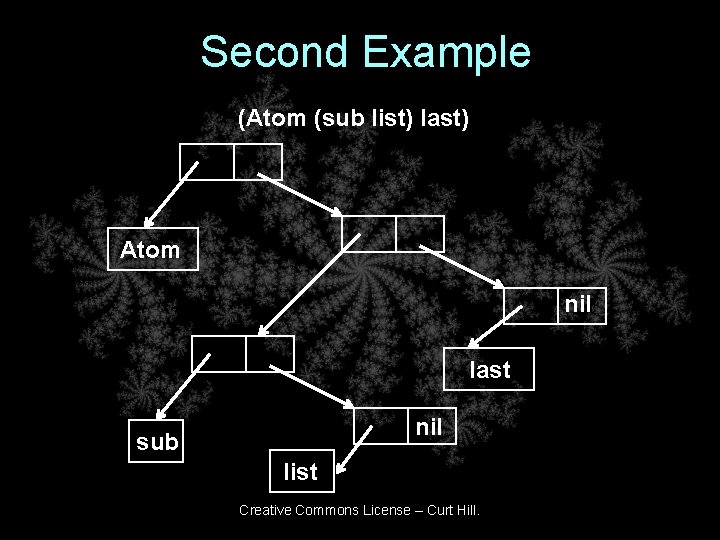
Lists • A list could be a simple list within parenthesis – (Three element list) • It could also have sub-lists – (Atom (A sub list) another (list)) – This is clearly not a linear list such as an STL List • LISP programs were also lists – The programs and data have same form Creative Commons License – Curt Hill.

Implementation • The LISP language was influenced by the machine on which it was developed • It had a 36 bit word that was partitioned into two pointers – Contents Address Register (CAR) – Contents Data Register (CDR) • An atom used the word for data • A list used the pointers and atoms • A list always ended in nil, a special pointer Creative Commons License – Curt Hill.

Example (Three element list) Three nil element List Creative Commons License – Curt Hill.

Second Example (Atom (sub list) last) Atom nil last nil sub list Creative Commons License – Curt Hill.

List Processing • There were two functions that were continually used in LISP to process a list • Car gave the first item of the list – Which could be a list itself • Cdr gave the rest of the list • A heavy dose of recursion and LISP could do it all Creative Commons License – Curt Hill.

Summary • Parse trees are N way • LISP trees are two way but keyless • Optimal search trees work better than balanced trees if frequencies are known in advance • Different directions in processing trees lead to different orders – Such as Infix or Reverse Polish from expression trees Creative Commons License – Curt Hill.