Other Sampling Methods Section 3 1 B Objective

Other Sampling Methods Section 3. 1 B

�Objective: To be able to understand implement other sampling techniques including systematic, stratified, cluster, and convenience sampling. �Purpose: To have the ability to choose the best sampling technique that would produce the best sample.

Why not SRS? �Sometimes it’s just not feasible or practical. �Sometimes there are statistical advantages to using more complex sampling methods.

Stratified Random Sample �Divide the population into groups of individuals that are similar in some way that is important to the response. �Choose a separate SRS in each stratum �Combine these to form the full

Stratified Sampling �Data is divided into subgroups (strata) �Strata are based specific characteristic �Age �Education level �Etc. �Use random sampling within each strata 5

Example To survey radio station about the most requested songs we randomly choose 100 radio stations from each geographic location.

Cluster Sample �Divide the population into groups or clusters. �Randomly choose some of these clusters. �All individuals in the chosen clusters are the sample

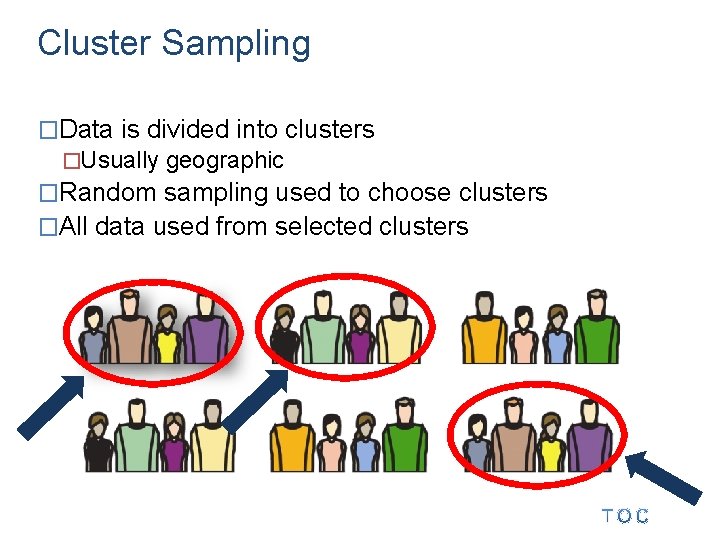
Cluster Sampling �Data is divided into clusters �Usually geographic �Random sampling used to choose clusters �All data used from selected clusters

Example of Cluster Survey AP students to see if they had enough time to take the test. We randomly pick some of the schools that took the test & every student at the selected schools are surveyed.

Systematic Sampling This is where you survey every kth person. You randomize it by randomly choosing where to start.

Systematic Sampling �All data is sequentially numbered �Every nth piece of data is chosen

�In a large city school system with 20 elementary schools, the school board is considering the adoption of a new policy that would require elementary students to pass a test in order to be promoted to the next grade. The PTA wants to find out whether parents agree with this plan. �Tell what type of sampling was used and what biases (if any) might result. �Don’t forget convenience and

�Put a big ad in the newspaper asking people to log their opinions on the PTA web site.

�Randomly select one of the elementary schools and contact every parent by phone.

�Send a survey hoe with every student, and ask parents to fill it out and return it the next day.

�Randomly select 20 parents from each elementary school. Send them a survey, and follow up with a phone call if they do not return the survey within a week.

�Run a poll on the local TV news, asking people to dial one of two phone numbers to indicate whether they favor or oppose the plan.

�Hold a PTA meeting at each of the 20 elementary schools and tally the opinions expressed by those who attend the meetings.

�Randomly select one class at each elementary school and contact each of those parents.

�Go through the district’s enrollment records, selecting every 40 th parent. PTA volunteers will go to those homes to interview the people chosen.

Example �A British farmer grows sunflowers for making sunflower oil. Her field is arranged in a grid pattern, with 10 rows and 10 columns as shown in the figure on the next page. Irrigation ditches run along the top and bottom of the field, as shown. The farmer would like to estimate the number of healthy plants in the field so she can project how much money she’ll make from selling them. It would take too much time to count the plants in all 100 squares, so she’ll accept an estimate based on a sample of 10 squares.

� Activity: Sampling Sunflowers using an SRS 10 grid squares using the rows as strata. Record the location (for example, B 6) of each square you select. Sampling and Surveys �Use Table D or technology to take an SRS of

� Activity: Sampling Sunflowers using Stratified � Use Table D or technology to take a stratified sample using the columns as strata and selecting one square from each column. Record the location (for example, B 6) of each square you select. Sampling and Surveys Sampling

� Activity: Sampling Sunflowers using Cluster � Use Table D or technology to take a cluster sample using the rows as strata and selecting one row as your sample. Record the location (for example, B 6) of each square you select. Sampling and Surveys Sampling

The table gives the actual # of sunflowers in each grid. Use this information to calculate your estimate of the mean number of sunflowers per square for each of your sample types. A B C D E F G H I J 1 106 104 106 105 105 108 107 106 2 103 104 103 105 3 101 99 102 101 100 102 101 4 98 99 99 99 100 99 98 101 99 101 5 98 100 100 99 99 99 98 100 98 6 97 98 98 98 99 99 97 98 7 103 102 104 101 102 102 104 102 8 104 103 103 102 103 104 102 9 106 104 106 102 107 104 103 106 10 107 108 109 110 106 107 109 107 106 107

How did you do? �The mean number of sunflowers in the population of all 100 grid squares in the field was 102. 46. �How did the 3 types of sampling methods do?

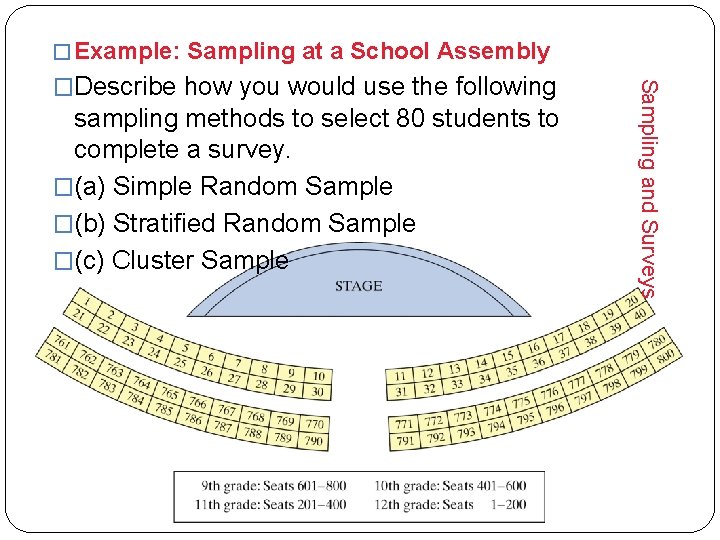
� Example: Sampling at a School Assembly sampling methods to select 80 students to complete a survey. �(a) Simple Random Sample �(b) Stratified Random Sample �(c) Cluster Sample Sampling and Surveys �Describe how you would use the following

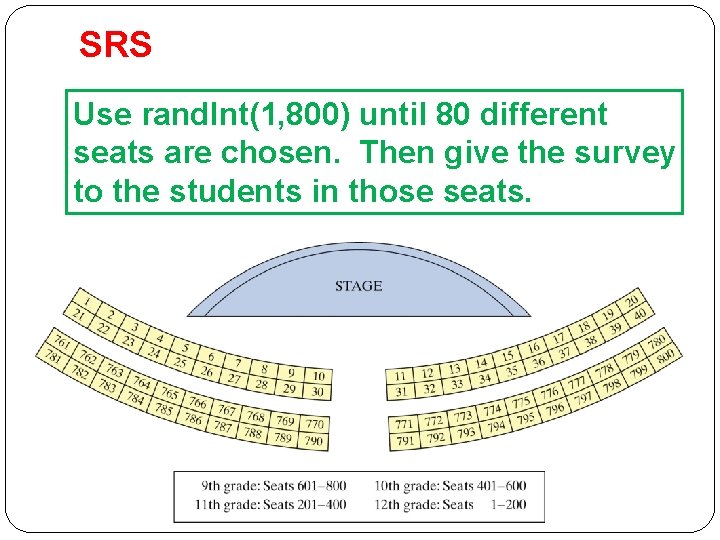
SRS Use rand. Int(1, 800) until 80 different seats are chosen. Then give the survey to the students in those seats.

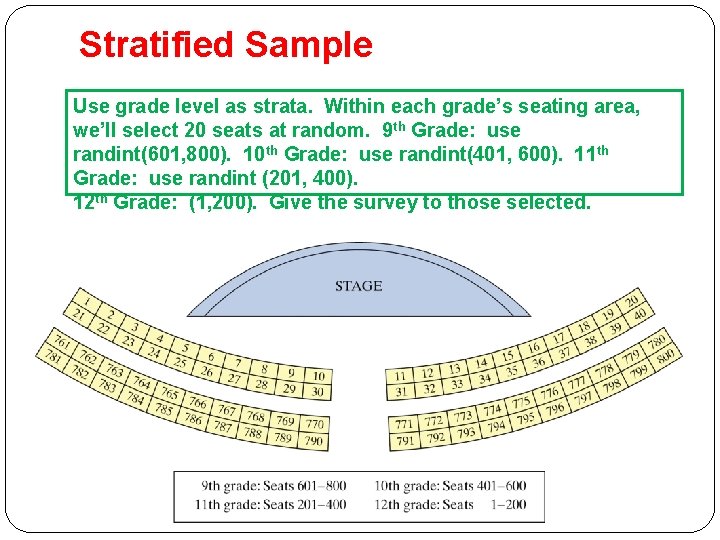
Stratified Sample Use grade level as strata. Within each grade’s seating area, we’ll select 20 seats at random. 9 th Grade: use randint(601, 800). 10 th Grade: use randint(401, 600). 11 th Grade: use randint (201, 400). 12 th Grade: (1, 200). Give the survey to those selected.

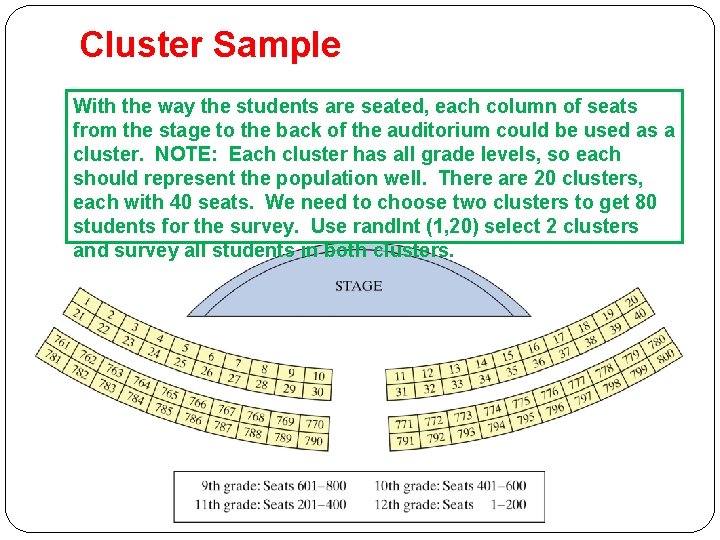
Cluster Sample With the way the students are seated, each column of seats from the stage to the back of the auditorium could be used as a cluster. NOTE: Each cluster has all grade levels, so each should represent the population well. There are 20 clusters, each with 40 seats. We need to choose two clusters to get 80 students for the survey. Use rand. Int (1, 20) select 2 clusters and survey all students in both clusters.

Inference �It is the process of drawing conclusions about a population on the basis of sample data. �Inferences from convenience samples or voluntary samples would be misleading because the methods are biased.

Activity �One at a time, each student will take a SRS of 20 chips and record the proportion of chips obtained that are red. �Dotplot of sample proportions:

Trusting Random Samples �Laws of probability all us to say how likely it is that sample results are close to the true population. �Laws of probability allow trustworthy inference about the population with a margin of error.

Margin of Error �Sets bounds on the size of the likely error. �Larger random samples give better information about the population than smaller samples.

Classwork �Bias Worksheet

Homework �Page 227 (17 -25) odd �Page 230 (37 -42)