Other QuasiExperimental Designs Design Variations Show specific design

  • Slides: 18
Download presentation
Other Quasi-Experimental Designs

Other Quasi-Experimental Designs

Design Variations Show specific design features that can be used to address specific threats

Design Variations Show specific design features that can be used to address specific threats or constraints in the context

Proxy Pretest Design N N l l O 1 X O 2 Pretest based

Proxy Pretest Design N N l l O 1 X O 2 Pretest based on recollection or archived data Useful when you weren’t able to get a pretest but wanted to address gain

Separate Pre-Post Samples N 1 N 2 l l l O X O O

Separate Pre-Post Samples N 1 N 2 l l l O X O O O Groups with the same subscript come from the same context. Here, N 1 might be people who were in the program at Agency 1 last year, with those in N 2 at Agency 2 last year. This is like having a proxy pretest on a different group.

Separate Pre-Post Samples N N l l l R 1 R 2 O X

Separate Pre-Post Samples N N l l l R 1 R 2 O X O O O Take random samples at two times of people at two nonequivalent agencies. Useful when you routinely measure with surveys. You can assume that the pre and post samples are equivalent, but the two agencies may not be.

Double-Pretest Design N N l l l O O X O O Strong in

Double-Pretest Design N N l l l O O X O O Strong in internal validity Helps address selection-maturation How does this affect selection-testing?

Switching Replications N N l l l O O X O O Strong design

Switching Replications N N l l l O O X O O Strong design for both internal and external validity Strong against social threats to internal validity Strong ethically

Nonequivalent Dependent Variables Design (NEDV) N N l l O 1 O 2 X

Nonequivalent Dependent Variables Design (NEDV) N N l l O 1 O 2 X O 1 O 2 The variables have to be similar enough that they would be affected the same way by all threats. The program has to target one variable and not the other.

NEDV Example l l l Only works if we can assume that geometry scores

NEDV Example l l l Only works if we can assume that geometry scores show what would have happened to algebra if untreated. The variable is the control. Note that there is no control group here.

NEDV Pattern Matching l l Have many outcome variables. Have theory that tells how

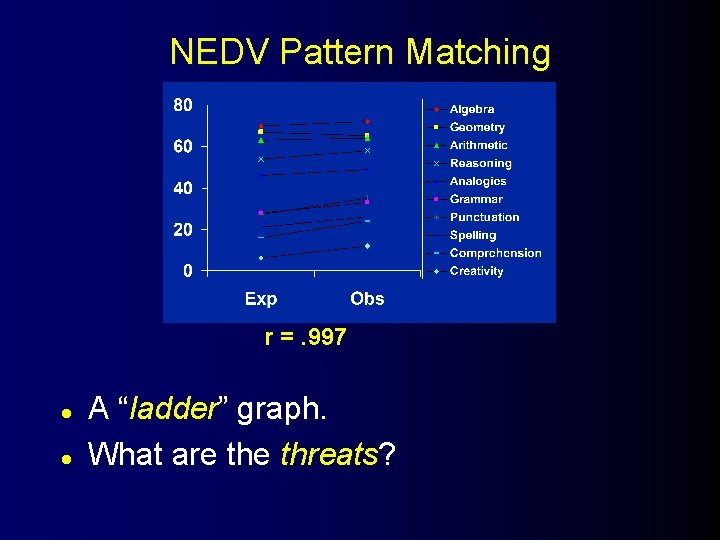
NEDV Pattern Matching l l Have many outcome variables. Have theory that tells how affected (from most to least) each variable will be by the program. Match observed gains with predicted ones. If match, what does it mean?

NEDV Pattern Matching r =. 997 l l A “ladder” graph. What are threats?

NEDV Pattern Matching r =. 997 l l A “ladder” graph. What are threats?

NEDV Pattern Matching l l l Single group design, but could be used with

NEDV Pattern Matching l l l Single group design, but could be used with multiple groups (could even be coupled with experimental design). Can measure left and right on different scales (e. g. , right could be t-values). How do we get the expectations?

Regression Point Displacement (RPD) N(n=1) O N O l l l X O O

Regression Point Displacement (RPD) N(n=1) O N O l l l X O O Intervene in a single site Have many nonequivalent control sites Good design for community-based evaluation

RPD Example l l Comprehensive community-based AIDS education Intervene in one community (e. g.

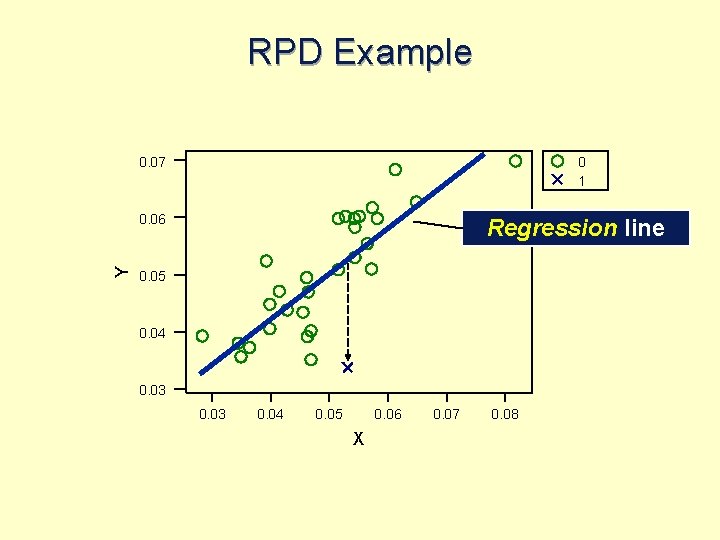
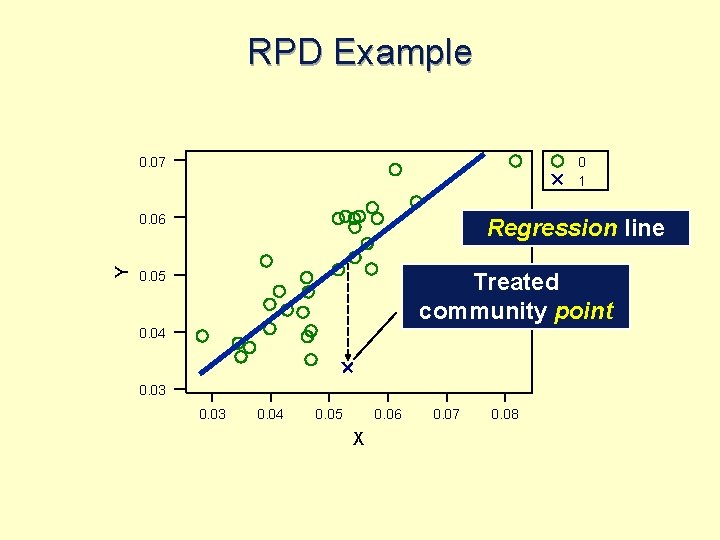
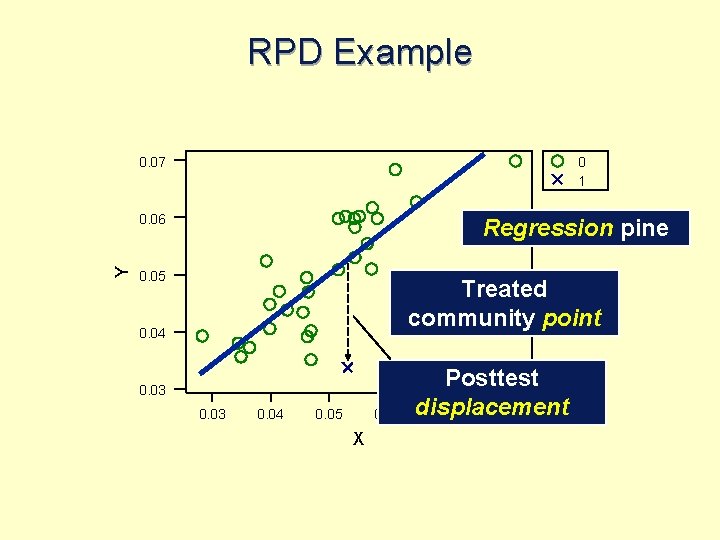
RPD Example l l Comprehensive community-based AIDS education Intervene in one community (e. g. , county) Have 29 other communities (e. g. , counties) in state as controls measure is annual HIV positive rate by county

RPD Example 0. 07 0 1 Y 0. 06 0. 05 0. 04 0.

RPD Example 0. 07 0 1 Y 0. 06 0. 05 0. 04 0. 03 0. 04 0. 05 0. 06 X 0. 07 0. 08

RPD Example 0. 07 0 1 Y 0. 06 Regression line 0. 05 0.

RPD Example 0. 07 0 1 Y 0. 06 Regression line 0. 05 0. 04 0. 03 0. 04 0. 05 0. 06 X 0. 07 0. 08

RPD Example 0. 07 0 1 Y 0. 06 Regression line 0. 05 Treated

RPD Example 0. 07 0 1 Y 0. 06 Regression line 0. 05 Treated community point 0. 04 0. 03 0. 04 0. 05 0. 06 X 0. 07 0. 08

RPD Example 0. 07 0 1 Y 0. 06 Regression pine 0. 05 Treated

RPD Example 0. 07 0 1 Y 0. 06 Regression pine 0. 05 Treated community point 0. 04 0. 03 0. 04 0. 05 0. 06 X Posttest displacement 0. 07 0. 08

QUASIEXPERIMENTAL DESIGNS SMALL N DESIGNS CORRELATIONAL DESIGNS WeekQUASIEXPERIMENTAL DESIGNS SMALL N DESIGNS CORRELATIONAL DESIGNS Week
QuasiExperimental Designs Learning Outcomes 1 Identify a quasiexperimentalQuasiExperimental Designs Learning Outcomes 1 Identify a quasiexperimental
Research Designs Comparing Groups 8 Quasiexperimental designs QuasiexperimentsResearch Designs Comparing Groups 8 Quasiexperimental designs Quasiexperiments
NonExperimental designs Surveys Correlational Quasiexperimental designs Psych 231NonExperimental designs Surveys Correlational Quasiexperimental designs Psych 231
NonExperimental designs Correlational Quasiexperimental designs Psych 231 ResearchNonExperimental designs Correlational Quasiexperimental designs Psych 231 Research
Quasiexperiments Quasiexperimental designs Experimental designs for studies inQuasiexperiments Quasiexperimental designs Experimental designs for studies in
Design 3 quasiexperimental and nonexperimental designs Learning outcomesDesign 3 quasiexperimental and nonexperimental designs Learning outcomes
RESEARCH DESIGN Experimental Designs The specific research designsRESEARCH DESIGN Experimental Designs The specific research designs
NonExperimental designs Developmental designs SmallN designs Psych 231NonExperimental designs Developmental designs SmallN designs Psych 231
Experimental Group Designs Group Designs Simple Group DesignsExperimental Group Designs Group Designs Simple Group Designs
NonExperimental designs Developmental designs SmallN designs Psych 231NonExperimental designs Developmental designs SmallN designs Psych 231
NonExperimental designs Developmental designs SmallN designs Psych 231NonExperimental designs Developmental designs SmallN designs Psych 231
NonExperimental designs Developmental designs SmallN designs Psych 231NonExperimental designs Developmental designs SmallN designs Psych 231
Different Conceptual Designs Different Conceptual Designs Designs forDifferent Conceptual Designs Different Conceptual Designs Designs for
NonExperimental designs Correlational Quasiexperimental Psych 231 Research MethodsNonExperimental designs Correlational Quasiexperimental Psych 231 Research Methods
QUASIEXPERIMENTAL STUDY DESIGNS IN EVALUATING MEDICINES USE INTERVENTIONSQUASIEXPERIMENTAL STUDY DESIGNS IN EVALUATING MEDICINES USE INTERVENTIONS
Quantitative Research QuasiExperimental Designs Pretestposttest Survey Research NonequivalentQuantitative Research QuasiExperimental Designs Pretestposttest Survey Research Nonequivalent