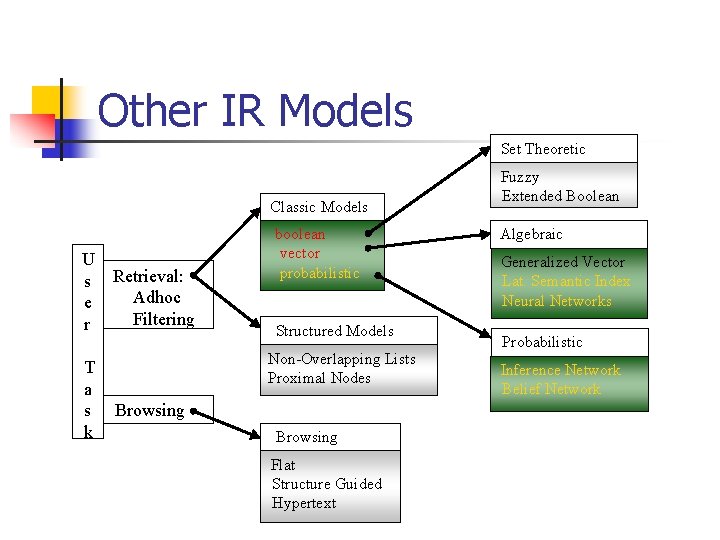
Other IR Models Set Theoretic Classic Models U

Other IR Models Set Theoretic Classic Models U s e r T a s k Retrieval: Adhoc Filtering boolean vector probabilistic Structured Models Non-Overlapping Lists Proximal Nodes Browsing Flat Structure Guided Hypertext Fuzzy Extended Boolean Algebraic Generalized Vector Lat. Semantic Index Neural Networks Probabilistic Inference Network Belief Network

Another Vector Model: Motivation Index terms have synonyms. [Use thesauri? ] 2. Index terms have multiple meanings (polysemy). [Use restricted vocabularies or more precise queries? ] 3. Index terms are not independent; think “phrases”. [Use combinations of terms? ] 1.

Latent Semantic Indexing/Analysis n n Basic Idea: Keywords in a query are just one way of specifying the information need. One really wants to specify the key concepts rather than words. Assume a latent semantic structure underlying the term-document data that is partially obscured by exact word choice.

LSI In Brief n Map from terms into lower dimensional space (via SVD) to remove “noise” and force clustering of similar words. n n Pre-process corpus to create reduced vector space Match queries to docs in reduced space

SVD for Term-Doc Matrix Terms Docs = mxm txd C mxd txm = where m is the rank of X (<=min(t, d)), T is orthonornal matrix of eigenvectors for term-term correlation, D is orthonornal matrix of eigenvectors from transpose of doc-doc correlation

Reducing Dimensionality n n n Order singular values in S 0 by size, keep the k largest, and delete other rows/columns in S 0, T 0 and D 0 to form Approximate model is the rank-k model with best possible least-squares-fit to X. Pick k large enough to fit structure, but small enough to eliminate noise – usually ~100 -300.

Computing Similarities in LSI n How similar are 2 terms? n n How similar are two documents? n n dot product between two row vectors of dot product between two column vectors of How similar are a term and a document? n value of an individual cell

Query Retrieval n n As before, treat query as short document: make it column 0 of C First row of C provides rank of docs wrt query.

LSI Issues n Requires access to corpus to compute SVD n n How to efficiently compute for Web? What is the right value of k ? Can LSI be used for cross-language retrieval? Size of corpus is limited: “one student’s reading through high school” (Landauer 2002).

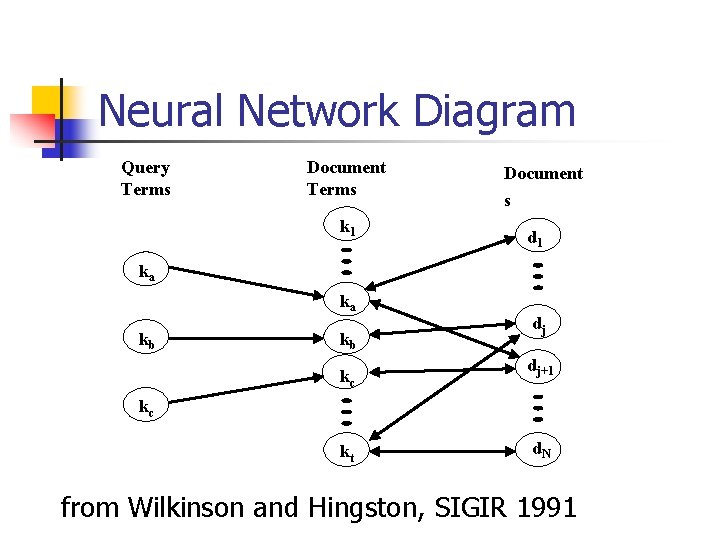
Other Vector Model: Neural Network n Basic idea: n n n 3 layer neural net: query terms, documents Signal propagation based on classic similarity computation Tune weights.

Neural Network Diagram Query Terms Document Terms k 1 Document s d 1 ka ka kb kb kc dj dj+1 kc kt d. N from Wilkinson and Hingston, SIGIR 1991

Computing Document Rank n Weight from query to document term n Wiq = wiq sqrt ( i wiq ) n Weight from document term to document n Wij = wij sqrt ( i wij )

Probabilistic Models Principle: Given a user query q and a document d in the collection, estimate the probability that the user will find d relevant. (How? ) n n n User rates a retrieved subset. System uses rating to refine the subset. Over time, retrieved subset should converge on relevant set.

Computing Similarity I relevant probability that document dj is relevant to query q, that dj is non-relevant to the query q, of randomly selecting dj from set R that a randomly selected document is

Computing Similarity II probability that index term ki is present in document randomly selected from R, Assumes independence of index terms

Initializing Probabilities n n assume constant probabilities for index terms: assume distribution of index terms in non-relevant documents matches overall distribution:

Improving Probabilities Assumptions: n approximate probability given relevant as % docs with index i retrieved so far: n approximate probabilities given nonrelevant by assuming not retrieved are non-relevant:

Classic Probabilistic Model Summary n Pros: n n n ranking based on assessed probability can be approximated without user intervention Cons: n n n really need user to determine set V ignores term frequency assumes independence of terms

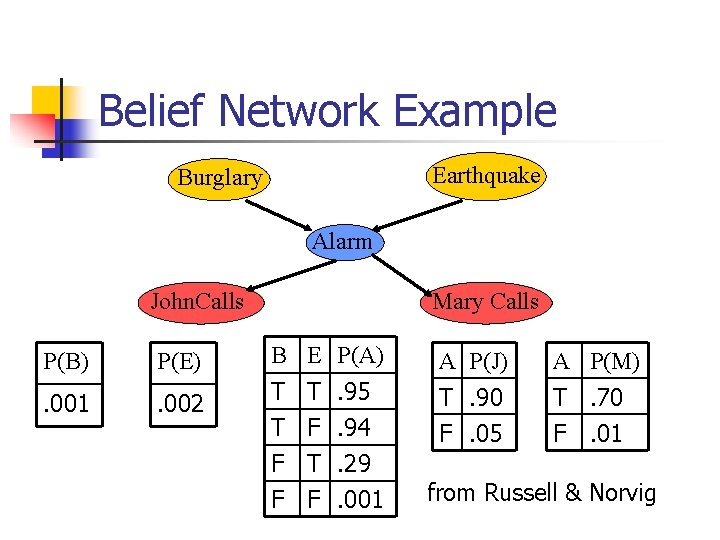
Probabilistic Alternative: Bayesian (Belief) Networks A graphical structure to represent the dependence between variables in which the following holds: 1. a set of random variables for the nodes 2. a set of directed links 3. a conditional probability table for each node, indicating relationship with parents 4. a directed acyclic graph

Belief Network Example Earthquake Burglary Alarm John. Calls Mary Calls P(B) P(E) B E P(A) A P(J) A P(M) . 001 . 002 T T. 95 T F. 94 F T. 29 T. 90 F. 05 T. 70 F. 01 F F. 001 from Russell & Norvig

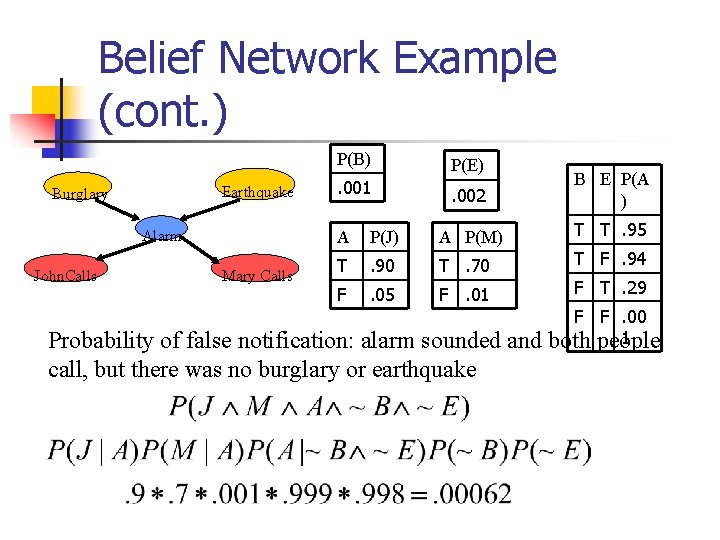
Belief Network Example (cont. ) P(B) Earthquake Burglary Alarm John. Calls Mary Calls . 001 P(E). 002 B E P(A ) A P(J) A P(M) T T. 95 T . 90 T. 70 T F. 94 F . 05 F. 01 Probability of false notification: alarm sounded and call, but there was no burglary or earthquake F T. 29 F F. 00 1 both people

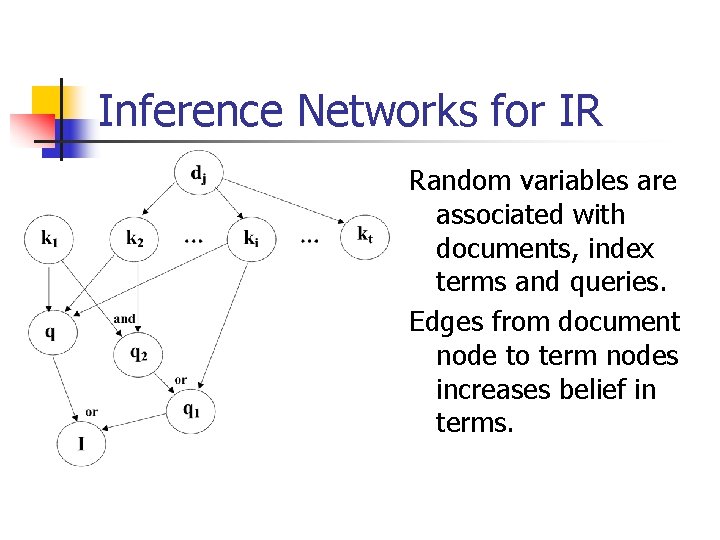
Inference Networks for IR Random variables are associated with documents, index terms and queries. Edges from document node to term nodes increases belief in terms.

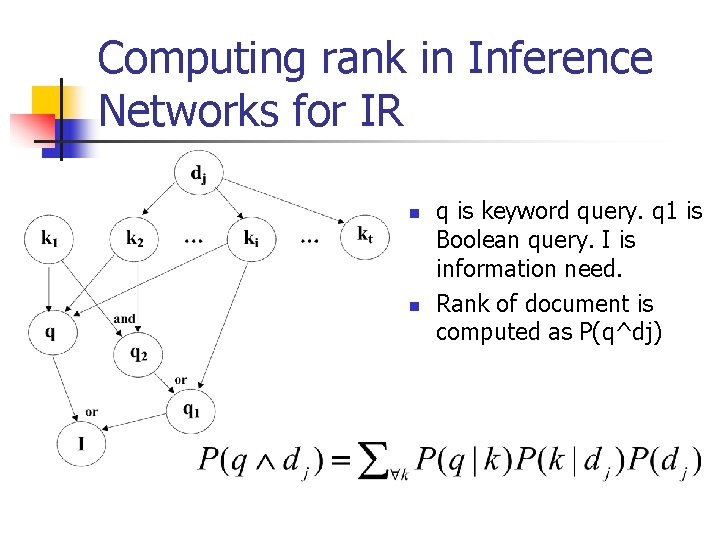
Computing rank in Inference Networks for IR n n q is keyword query. q 1 is Boolean query. I is information need. Rank of document is computed as P(q^dj)

Where do probabilities come from? (Boolean Model) n n n uniform priors on documents only terms in the document are active query is matched to keywords ala Boolean model

Belief Network Formulation n different network topology does not consider each document individually adopts set theoretic view