Other data types Standard type sizes b Most

Other data types

Standard type sizes b Most machines store integers and reals in 4 bytes (32 bits) b Integers run from -2, 147, 483, 648 to 2, 147, 483, 647 b This is 232 b Single precision reals run from -1038 to 1038

Representational problem Arithmetic errors are possible whenever real numbers are used in computing. b This is because only a limited number of bits are available to represent the exponent and mantissa of a real number. b The results are called b • overflow errors, and • underflow errors

Roundoff error b roundoff error occurs whenever a real number must be approximated to fit into the alloted space. (A+B)2 - 2 AB - B 2 b For example: A 2 + 2 AB + B 2 - 2 AB + B 2 = A 2 A 2

Roundoff error b The result should be 1, but may not turn out that way due to rounding errors. (A+B)2 - 2 AB - B 2 A 2 + 2 AB + B 2 - 2 AB + B 2 = A 2 A 2 = 1?

Solution? b One way to deal with rounding error is to increase the size (number of bits) used to represent your data. b Instead of the defaults, we ‘parameterize’ the data types. . .

Parameterized types b A parameterized type is one that can be used to construct larger configurations of a native type b You use parameterized types when you suspect that the size of a conventional native type will not accommodate the size of the values you could encounter. b You also use parameterized types to reduce the size of a representation.
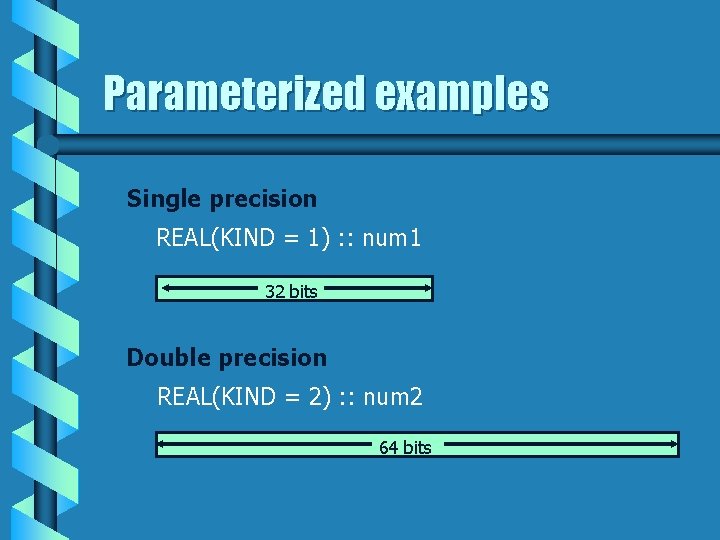
Parameterized examples Single precision REAL(KIND = 1) : : num 1 32 bits Double precision REAL(KIND = 2) : : num 2 64 bits
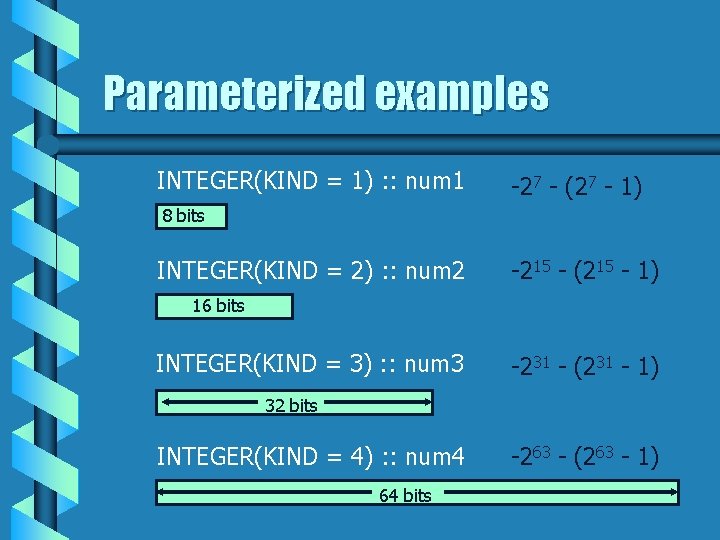
Parameterized examples INTEGER(KIND = 1) : : num 1 -27 - (27 - 1) 8 bits INTEGER(KIND = 2) : : num 2 -215 - (215 - 1) 16 bits INTEGER(KIND = 3) : : num 3 -231 - (231 - 1) 32 bits INTEGER(KIND = 4) : : num 4 64 bits -263 - (263 - 1)

Functions for parameterized types b There a series of functions that allow us to establish and manipulate data of parameterized types b These functions are unique to the Fortran 90 language

SELECTED_REAL_KIND(p, r) This function returns the KIND type that is necessary for a real number to store a value with p decimal digits of precision within the range of r, where r is a power of 10. Example: To store the value 1. 2345678901234567890 we need 29 decimal digits (precision) SELECTED_REAL_KIND(29, 3) for values between -1, 000 and 1, 000 REAL(KIND = SELECTED_REAL_KIND(29, 3)) : : num

SELECTED_INT_KIND(r) This function returns the KIND type that is necessary for an integer number to store a value within range r such that 10 -r <= num <= 10 r Example: SELECTED_INT_KIND(9) for values between -1, 000, 000 and 1, 000, 000 INTEGER(KIND = SELECTED_INT_KIND(9)) : : num

PRECISION(num) This function returns the number of decimal digits of precision for a variable. Example: To store the value 1. 2345678901234567890 we need 29 decimal digits (precision) REAL(KIND = SELECTED_REAL_KIND(29, 3)) : : num PRINT*, “The precision of num is: “, PRECISION(num)

RANGE(num) This function returns the range of the exponents for a given value. Example: REAL(KIND = SELECTED_REAL_KIND(29, 3)) : : num PRINT*, “The range of num is from 10^-”, RANGE(num), & “- 10^”, RANGE(num)

Other native data types b Complex numbers • contain both a real and imaginary part b Characters • used primarily for character strings • we have already made use of some of these.

type COMPLEX b COMPLEX numbers have both a real and imaginary part (a + bi) where i is the square root of negative 1. b COMPLEX is a native type in FORTRAN 90 but not in earlier versions of the language.

Operator overloading b Since COMPLEX number addition does not follow the same pattern that standard INTEGER or REAL addition does we need a new version of it. b COMPLEX : : z, w b z = (3, 4) b w = (5, 2) b PRINT*, z + w

COMPLEX addition Given two COMPLEX numbers z and w such that z = a + bi and w = c + di The general formula for COMPLEX number addition is: z + w = (a + c) + (b + d)i z = (3, 4) w = (5, 2) PRINT*, z + w (8, 7)

COMPLEX subtraction Given two COMPLEX numbers z and w such that z = a + bi and w = c + di The general formula for COMPLEX number addition is: z - w = (a - c) + (b - d)i z = (3, 4) w = (5, 2) PRINT*, z - w (-2, 2)

COMPLEX product Given two COMPLEX numbers z and w such that z = a + bi and w = c + di The general formula for COMPLEX number multiplication is: z * w = (ac - bd) + (ad - bc)i z = (3, 4) w = (5, 2) PRINT*, z * w (7, -14)

COMPLEX quotient Given two COMPLEX numbers z and w such that z = a + bi and w = c + di The general formula for COMPLEX number division is: z / w = (ac + bd)/(c 2 + d 2) + (bc - ad)/(c 2 + d 2)i z = (3, 4) w = (5, 2) PRINT*, z / w (4. 27, 2. 6)

Type CHARACTER b We have already used CHARACTER data to some extent. b CHARACTER data is, by default, represented using ASCII character codes. b ASCII stands for the American Standard Code for Information Interchange - it is the common method used by almost all computers.
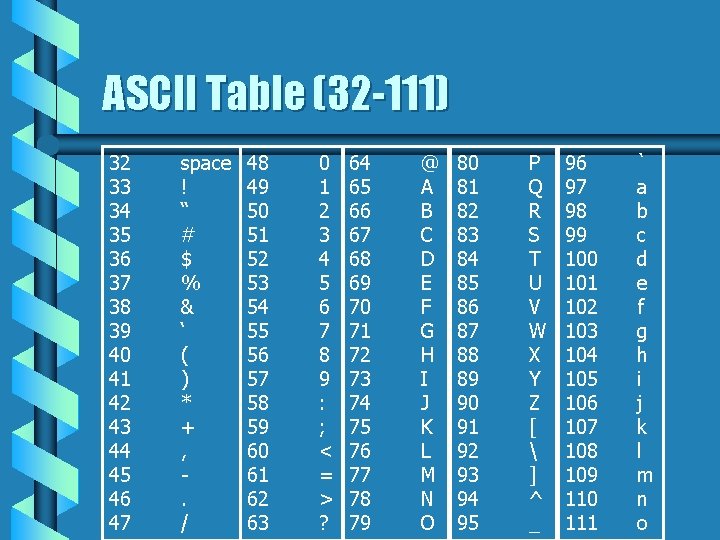
ASCII Table (32 -111) 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 space ! “ # $ % & ‘ ( ) * + , . / 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 0 1 2 3 4 5 6 7 8 9 : ; < = > ? 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 @ A B C D E F G H I J K L M N O 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 P Q R S T U V W X Y Z [ ] ^ _ 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 ` a b c d e f g h i j k l m n o

Character substrings b A substring is a portion of a main string b Example • • • CHARACTER(20) : : name = “George Washington” PRINT*, name(: 20) George Washington PRINT*, name(: 8) George W PRINT*, name(8: ) Washington PRINT*, name(8: 11) Wash

CHARACTER operators b Concatenation • • • (//) CHARACTER(6) : : fname CHARACTER(9) : : lname fname = “George” lname = “Washington” PRINT*, lname // “, “ // fname b Output • Washington, George

String to string functions b ADJUSTL(str) - left justifies the string str b ADJUSTR(str) - right justifies the string str b REPEAT(str, n) - makes string consisting of n concatenations of the string str b TRIM(str) - removes trailing blanks

Examples b CHARACTER(20) : : name 1, name 2, name 3 b name = “Buffalo Bill” b name 2 = ADJUSTR(name 1) Buffalo Bill b name 3 = ADJUSTL(name 2) Buffalo Bill b PRINT*, REPEAT(name 1(1: 1), 5) BBBBB b PRINT*, TRIM(name 3) Buffalo_Bill

Relational operators b The standard relational operators <, <=, >, >=, ==, /= all work with character variables. b IF ( name 1 > name 2) THEN… b They compare the values of the ASCII characters in corresponding positions until they can determine that one is less than the other.

Conversion Functions b ICHAR - converts a character to an integer b CHAR - converts an integer to a character b These use ASCII values by default.

Examples INTEGER : : num, i, sum CHARACTER(10) : : numeral DO i=1, 10 numeral(i: i) = CHAR(i+47) ENDDO PRINT*, numeral 0123456789 sum = 0 DO i = 1, 10 sum = sum + (ICHAR(numeral(i: i))-47) ENDDO PRINT*, “sum is “, sum is 45

File Processing

Types of files b We have already dealt with reading data from standard ASCII text files into our program. b This sort of file is called a ‘sequential access’ file. b Sequential access means that in order to get to a desired record you must first have read and processed all records before it in sequence.

Direct access files b A direct access file is an alternative to sequential access. b In a direct access file you do not need to read the lines of the file in sequence. b You can get to any record on the file by accessing the storage locations directly. b You would want to use this for very large data files where reading the whole thing into arrays is out of the question.

How direct access works b If a file is stored on disk, then individual records can be accessed directly if we know • The address of where the file starts • How long each record is (all must be the same length) b This means that when the file was OPENED we must know it’s record length (RECL) b When reading we must specify the record.

Example OPEN (12, FILE=“student. dat”, ACCESS=“DIRECT”, & RECL=48) ! This file contains 100 student records. The id numbers ! On the file go from 001 to 100. The records are sorted. DO PRINT*, “Please enter an id number” READ*, id IF ((id > 0). and. (id < 100)) READ(12, ‘(1 x, a 15, i 5, a 5, f 4. 0, f 6. 2)’, REC=id) & lname, fname, id, passwd, limit, used ENDDO

Pointers

Pointer variables b A pointer is an integer that contains the address of a data item in memory. 0243632 Smith 0243632

Allocating pointers Pointers are created through the ALLOCATE statement. First, however, we must declare the pointer: CHARACTER(8), POINTER : : nameptr CHARACTER(8) : : name = “Smith” ALLOCATE(nameptr) nameptr => name ! NOTE: the => operator means ‘assign pointer of’

Pointer variables b Result after the last code segment name 0243632 Smith nameptr 0243632

Assignment to pointers Pointers are created through the ALLOCATE statement. First, however, we must declare the pointer: CHARACTER(8), POINTER : : nameptr ALLOCATE(nameptr) nameptr = “Smith” ! Memory has been allocated for 8 characters and ! nameptr points to that memory. Then “Smith” is ! Placed in that location.

Pointer variables b Result after the last code segment 0243632 Smith nameptr 0243632

ASSOCIATED b The ASSOCIATED function tells you whether a pointer actually points to any data. b IF (. not. ASSOCIATED(nameptr)) THEN b PRINT*, nameptr is null b ENDIF

Why are pointers important? b Up until now we have used only ‘static’ structures. b A static structure is one that is defined and has space allocated for it - at compile time. b This means it’s size is fixed. Example: the normal array b Pointer however are dynamic! They allow us to create memory cells at runtime.

Dynamic data structures b A dynamic structure is one that can grow or contract as the program executes, to accommodate the data that is being processed. b Dynamic structures waste little memory. b They can also allow new forms of data organization (rather than always using arrays) b More on this next lecture.
- Slides: 44