Other Arithmetic Functions Section 4 5 Combinational Multiplier

Other Arithmetic Functions Section 4 -5

Combinational Multiplier Example: • 4 -Bit Multiplicand B = {B 3 B 2 B 1 B 0} • 3 -Bit Multiplier A = {A 2 A 1 A 0} • Product is a 7 -Bit number, C = {C 6 C 5 C 4 C 3 C 2 C 1 C 0 } 2

Computing the Product • Let us work out the multiplication on the board: 3
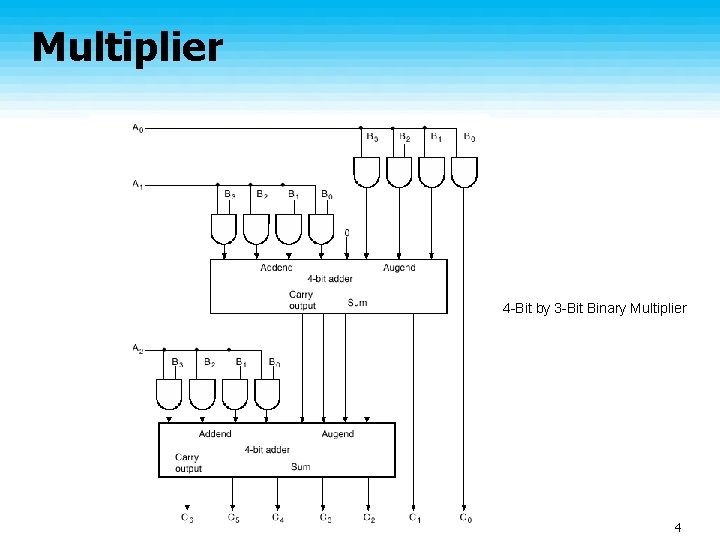
Multiplier 4 -Bit by 3 -Bit Binary Multiplier 4

Contraction Can implement other functions ( Like increment, decrement ) by using basic arithmetic circuits (e. g. Adder) And removing unused portions • This is called contraction 5

Incrementing • Very common ♦ Computation of memory address for the next instruction to execute by CPU • Use a customized adder To increment A = { A 2 A 1 A 0 }, do A 2 A 1 A 0 + 001; Do not use C 3 (why? ) Hiding Box Hiding Box 6
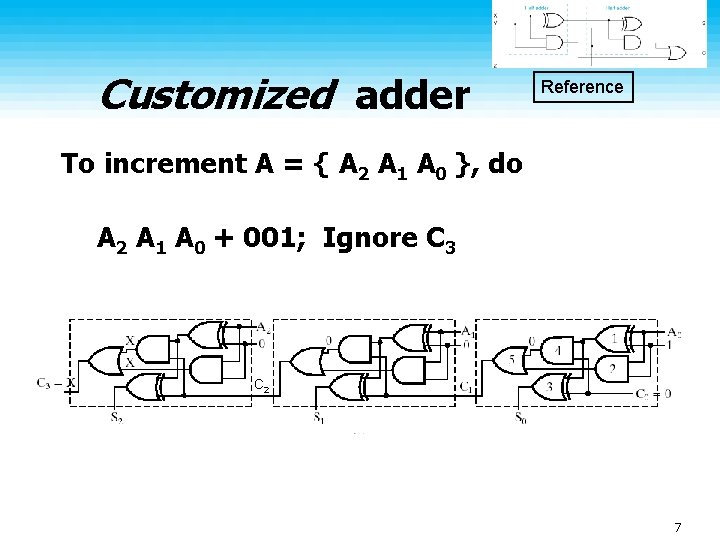
Customized adder Reference To increment A = { A 2 A 1 A 0 }, do A 2 A 1 A 0 + 001; Ignore C 3 C 2 7
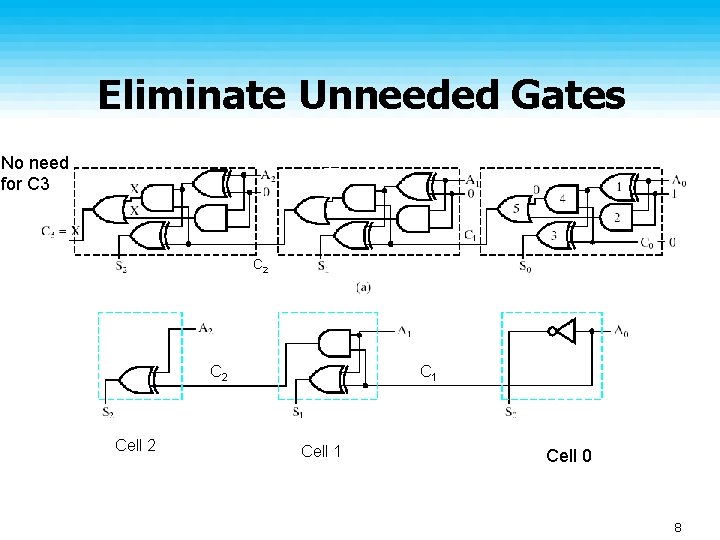
Eliminate Unneeded Gates No need for C 3 0 C C 22 C 2 Cell 2 C 1 Cell 0 8

Multiplication by Constant Case 1: Constant is a power of two Case 2: Constant is NOT a power of two 9

Multiplication by Power of 2 • Just wires C=4*B • Division by power of 2 similar C=B/4 10
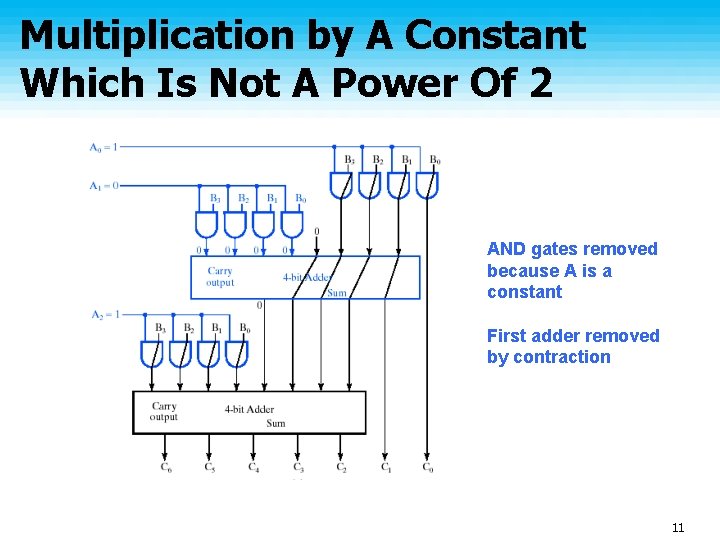
Multiplication by A Constant Which Is Not A Power Of 2 AND gates removed because A is a constant First adder removed by contraction 11

Contraction Not Always Best • Sometimes it pays to rethink the function ♦ Example: study decrementer in book (Example 4 -6 page 167) 12

Sign Extension • Changing the number of bits used to store a number is common • Example: ♦ -5 in stored in 4 -bits (1011) ♦ to store -5 in 8 bits, extend the “Sign Bit” in the 4 left most bits • 1011 is changed to 1111 1011 Ø 1011 = -5 Ø 1111 1011 is also -5 13

We’ve Covered • Adders ♦ Ripple carry • Subtracting unsigned numbers ♦ New design for adder-subtractor • Signed numbers ♦ Signed addition/subtraction • Multiplication – just basic • Modified Circuits 14
- Slides: 14