OSNOVNI POJMOVI TEORIJE SKUPOVA Skupovi su deo naeg

OSNOVNI POJMOVI TEORIJE SKUPOVA • • Skupovi su deo našeg svakodnevnog života. Korpa jabuka, stado ovaca, svi kontinenti, populacija bakterija, tačke na kružnici, prirodni brojevi, sve su to primeri skupova. • Deca u vrtićima se upoznaju sa ovim pojmom. • Skoro svaka delatnost čoveka odnosi se na neke skupove. Danas su skupovi u matematici i nauci deo naše svakodnevice. • Interesantno je da pojam skupa je nastao tek u 19 veku.

OPERACIJE SA SKUPOVIMA • Unija dva skupa A i B je skup Primer: • U opštem slučaju, kada imamo konačno mnogo skupova , njihova unija je:

• Presek skupova A i B je skup Primer: • Ako je presek dva skupa A i B prazan, tada kažemo da su oni disjunktni. • Ako je dato konačno mnogo skupova njihov presek je:

• Ko je Dekart ? • Dekart • • • Rene (Descartes René, 1596. -1650. ) Bio je matematičar, filozof i naučnik čije je delo Geometrija (La geometrie) postavilo osnove današnjoj analitičkoj geometriji. Tvorac koordinatnog sistema Prvi koji je upotrebio poslednja slova alfabeta da označi nepoznate veličine Začetnik je novog filozofskog pravca Racionalizma. Metodskim skeptičkim raščišćavanjem svega nejasnog i nesigurnog, izdvajanjem i odbacivanjem nepouzdanog, Dekart dolazi do osnovne istine, koja je po njegovom mišljenju potpuno pouzdana i iz koje će nastojati da izvede čitav svoj filozofski sistem. Ta istina je sadržana u njegovoj poznatoj rečenici "Mislim, dakle postojim" (Cogito, ergo sum).

• Izloženi pojmovi predstavljaju takozvanu Naivnu teoriju skupova čiji se pojmovi intuitivno prihvataju. • Njen tvorac je nemački matematičar Džorž Kantor (Georg Kantor 1845. 1918. ) Mada njegova otkrića u prvo vreme izazivaju sumnje pa i otvorena protivljenja matematičara toga doba, teorija skupova počinje da se široko primenjuje u mnogim matematičkim disciplinama i praksi. •

BROJ ELEMENATA SKUPAKARDINALNI BROJ • • Određivanje broja elemenata konačnih skupova svodi se na njihovo prebrojavanje. Kada se radi o beskonačnim skupovima , problem je znatno složeniji. • Pojam kardinalnog broja je uveden da bi se pomoću njega beskonačni skupovi mogli upoređivati po veličini. • Još u 17 veku čuveni fizičar i matematičar Galileo Galilej (Galileo Galilei 1564 -1642) je primetio da kod beskonačnog skupa, njegov pravi podskup može biti iste veličine kao i ceo skup. • Kasnije u 19. veku je uočeno da svi beskonačni skupovi nisu iste veličine, da neki beskonačni skupovi mogu biti veći od drugih beskonačnih skupova. Primer: Skup N- prirodnih brojeva i 2 N parnih brojeva Skup N- prirodnih brojeva i Z celih brojeva

• • Šta je kardinalni broj? Kod konačnih skupova, kardinalni broj predstavlja broj elemenata skupa. • • A kod beskonačnih skupova? Ako postoji bijektivna funkcija f skupa A na skup B , onda se za skupove A i B kaže da imaju isti kardinalni broj, u oznaci k. A=k. B ili card. A=card. B. • • Skup N je prebrojiv. Proizvoljan skup A je prebrojiv ako se može poređati u niz. • Ako je skup A prebrojiv onda ima isti kardinalni broj kao skup prirodnih brojeva N • Kardinalni broj skupa prirodnih brojeva označava se sa hebrejskim slovom i čita se alef nula

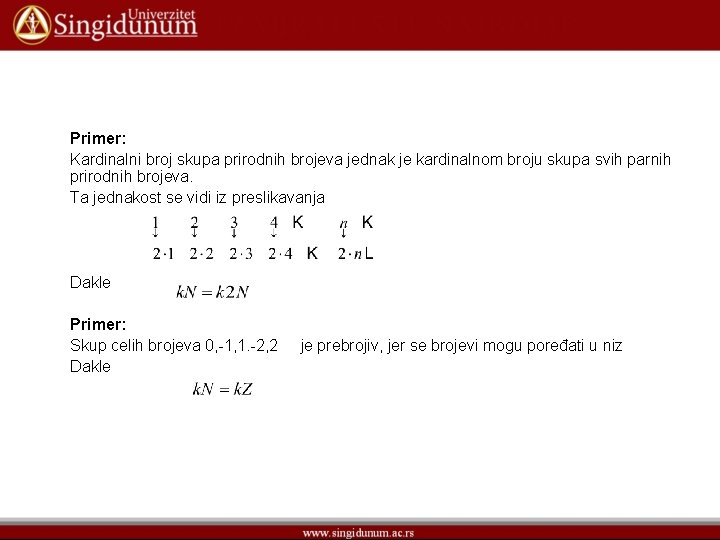
Primer: Kardinalni broj skupa prirodnih brojeva jednak je kardinalnom broju skupa svih parnih prirodnih brojeva. Ta jednakost se vidi iz preslikavanja Dakle Primer: Skup celih brojeva 0, -1, 1. -2, 2 je prebrojiv, jer se brojevi mogu poređati u niz Dakle

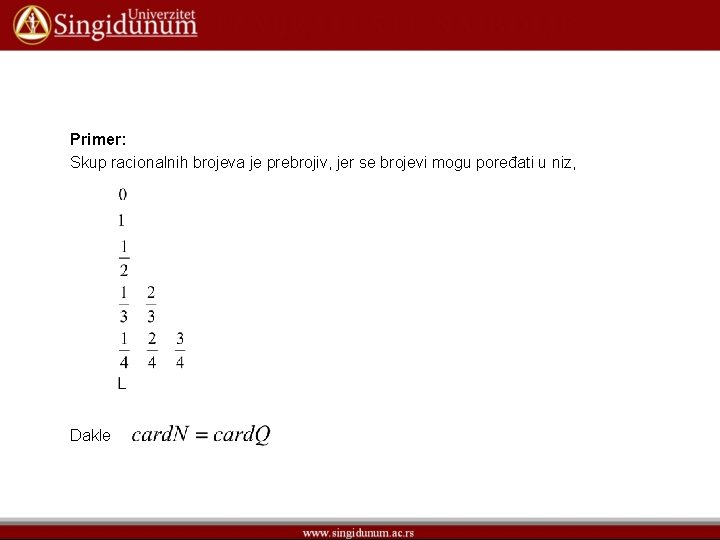
Primer: Skup racionalnih brojeva je prebrojiv, jer se brojevi mogu poređati u niz, Dakle

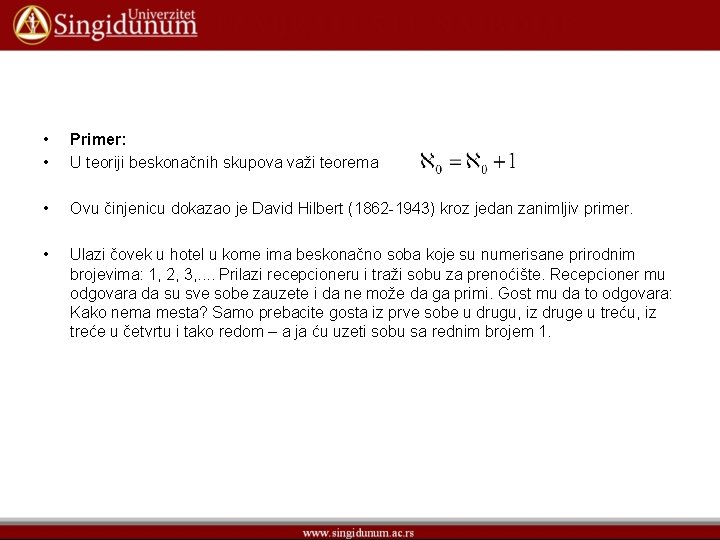
• • Primer: U teoriji beskonačnih skupova važi teorema • Ovu činjenicu dokazao je David Hilbert (1862 -1943) kroz jedan zanimljiv primer. • Ulazi čovek u hotel u kome ima beskonačno soba koje su numerisane prirodnim brojevima: 1, 2, 3, . . Prilazi recepcioneru i traži sobu za prenoćište. Recepcioner mu odgovara da su sve sobe zauzete i da ne može da ga primi. Gost mu da to odgovara: Kako nema mesta? Samo prebacite gosta iz prve sobe u drugu, iz druge u treću, iz treće u četvrtu i tako redom – a ja ću uzeti sobu sa rednim brojem 1.

• U trenutku kada se teorija skupova počela da prihvata i primenjuje uočavaju se njeni nedostaci, prvi paradoksi. • Prvi uočava sam Kantor 1895 g, pa Rasel, a zatim i mnogi drugi. • Otkrivanje paradoksa u teoriji skupova uticalo je na razvoj matematičke logike i dalji razvoj teorije skupova

• U čemu je bio problem? • U naivnoj teoriji skupova pojmovi nisu bili strogo definisani, odnosno bili su definisani preko osobina svojih članova i mogli su se tumačiti na različite načine. • Glavni problem naivne teorije skupova je bio uslov kojim se elementi grupišu u skup. Tako su uočene i prve protivrečnosti, odnosno paradoksi. Šta su paradoksi? Paradoks lažova Najstariji varijanta paradoksa je tvrđenje čuvenog kritskog filozofa Epimenida koji glasi: Krićanin kaže ˝ Svi krićani lažu˝ • • •

• • Najčuveniji paradoks je Raselov paradoks nastao 1902 godine, (Bertrand Rasel 1872 -1970). Time je ukazano na nedostatke takozvane naivne teorije skupova. Uočio je da ako se skupovi definišu preko osobina svojih članova neki skupovi će biti sami sebi elementi, a drugi neće. Postoje razne interpretacije Raselovog paradoksa, paradoks brijača, paradoks biblioteke, Pinokija, lažova, i mnogi drugi.

• • Paradoks brijača U nekom selu živeo je brijač, koji je brijao sve one stanovnike sela, koji se nisu brijali sami. Da li je brijač brijao samog sebe? • • Ako bi se brijač brijao sam, on bi bio jedan od stanovnika koji se briju sami, pa se ne bi smeo brijati kod brijača, odnosno kod samog sebe. Ako suprotno brijač ne bi brijao sam, bio bi jedan od stanovnika sela koji se ne briju sami, pa bi se morao brijati kod brijača, odnosno kod sebe. Znači imamo kontradikciju. • • Kako se rešava ovaj paradoks? Jednostavno, možemo zaključiti da takvo selo ne postoji.

• • Raselov paradoks je ukazao da Kantorova prihvaćena definicija skupa nije održiva i da skup nije sve što nam padne na pamet, već da se pojam skupa mora suziti. Rasel je uočeni problem rešio tako što je definisao pojam klase i jedan od načina prevazilaženja ovog paradoksa se svodi da se skup svih skupova ne smatra skupom, već klasom, koja je uopštenje pojma skupa. Klasa takođe nema strogu definiciju, već možemo reći da nju čine objekti odabrani po nekom zajedničkom kriterijumu. Pojam klase se razlikuje od pojma skupa, jer se skup se može shvatiti kao unija bilo kakvih elemenata.

• • • • U matematici su se razvila tri pravca kojima je pokušano da se reše nastali problemi. Raselov–logicizam ( smatrali su da se matematika može svesti na logiku ), Bauerov-intuicionalizam (osnovna ideja bila je da se postojanje objekta priznaje samo ako postoji način za njegovu konstrukciju) Hilbertov–formalizam (eliminisati iz matematike sve nedoumice i dvosmislenosti koje izaziva prirodan jezik. Napraviti veštacki jezik za matematiku u kome će pravila biti tako precizna, tako kompletna da neće biti nedoumica da li je neki dokaz ispravan ili nije)

• Problem paradoksa rešilo se definisanjem aksiomatike teorije skupova Aksiome teorije skupova. • • • Prvi aksiomatski pristup dao je Zermelo 1908. godine, a posle njega i mnogi drugi matematičari. Zermelov pristup problemu suštinski se razlikovao od ostalih matematičara koji su se bavili ovim problemom. Skupovi nisu zasnovani na podeli na dva dela, odnosno na one koji imaju i na one koji nemaju zadatu osobinu. Po njemu skupovi nastaju postepeno, kumulativno, polazeći od praznog skupa kao polaznog i svaki skup se može izgraditi pomoću njega jednostavnim operacijama. Skup može da sadrži samo one skupove koji su izgrađeni pre njega.

• Kao posledicu svih nedoumica koje su se javile, nemački matematičar David Hilbert, početkom 20 veka postavio je tri pitanja: • • • Da li je matematika kompletna? Da li je matematika konzistentna ( dosledna, neprotivrečna)? Da li je matematika odlučiva? • Na prva dva pitanja odgovorio je Kurt Gedel (1906 -1978), a na poslednje Alan Tjurig (1921 -1954). Odgovori su bili krajnje neočekivani i pokazalo se da Hilbertova vizija da formalizuje celu matematiku nije moguća.

Kompletnost • • Najveći potres u matematici 20 veka izazvao je 1931. godine Kurt Gedel. Dokazao je da matematika nikada ne može biti logički savršena, odnosno da postoje problemi koji mogu biti nerešivi. Znači matematika nije kompletna. Gedel je ukazao da postoje tvrđenja koje se ne mogu dokazati, Alip. Postoji mnogo tvrđenja koje mogu biti dokazana, pa njegov dokaz nije poremetio ništa što je bilo dokazano u prošlosti. Mnogi matematičari su verovali da se Gedelove teoreme odnose samo na najekstremnije oblasti matematike i da se zbog toga ne moraju njima baviti. Gedel je rekao da nedokazive teoreme postoje, ali nije mogao da kaže koje su. 1963. godine, Pol Koen, dvadesetdevetogodišnji matematičar sa Stanforda, razvio je tehniku za testiranje neodlučivosti određenog pitanja. On je bio prva osoba koja je otkrila specificna pitanja koja su zaista bila neodlučiva

Konzistentnost • • Kurt Godel i Alan Tjuring pokazali su da je nemoguće formalizovati celu matematiku, zato što je bilo koji formalni aksiomatski sistem ili nekonzistentan ili nepotpun. U slobodnoj interpretaciji, svojstvo nekonzistentnosti (protivurečnosti) znači da sistem dokazuje i netačne teoreme, a svojstvo nepotpunosti znaci da sistem ne dokazuje sve valjane teoreme.

Odlučivost • • Oslučivost se svodi na postojanje efektivnog metoda za rešavanje nekog problema. Naprimer iračunljive teorije su: iskazni račun, bulova algebra, teorija množenja prirodnih brojeva i sl Postoje i neodlučivi problemi: To su na primer, teorija grupa, predikatski račun i sl

• Kao posledicu ovih saznanja postavlja se pitanje: Kakvu sigurnost matematika pruža? • • • Ako nikada ne možemo imati potpun skup aksioma, tada nikada nećemo biti sigurni ni u šta. I ako pokušamo da dodamo nove aksiome nema garancija da ćemo dobiti potpunost teorije. Kurt Godel i Alan Tjuring pokazali su da je nemoguće formalizovati celu matematiku, zato što je bilo koji formalni aksiomatski sistem ili nekonzistentan ili nepotpun.

• Praktična posledica Gedelove teoreme odnosi se na računare. • Kako je njihova teorijska podloga formalna aritmetika, a okvir problema dostupan računaru daleko uži u poređenju sa okvirom dostupnom ljudskom mozgu. Činjenica da skoro svaki kompjutersko programski jezik može da podrži sve postojeće algoritme je veoma bitan oblik potpunosti. • • To je teorijska osnova za celo računarstvo. Tako je formalizam trijumfovao ne u matematici, već u računarstvu. To je, bar za sada pozitivan rezultat, jer je čovek još uvek jaci od masine.