OSCILLAZIONI 1 Moto periodico Per moto periodico intendiamo

OSCILLAZIONI 1

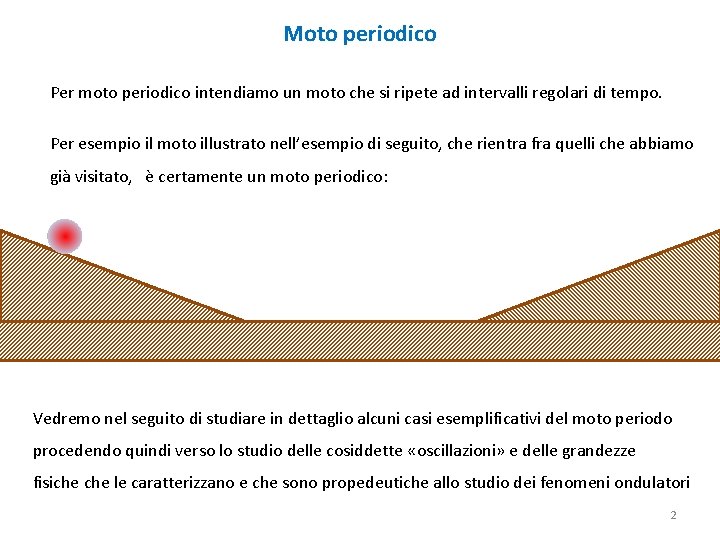
Moto periodico Per moto periodico intendiamo un moto che si ripete ad intervalli regolari di tempo. Per esempio il moto illustrato nell’esempio di seguito, che rientra fra quelli che abbiamo già visitato, è certamente un moto periodico: Vedremo nel seguito di studiare in dettaglio alcuni casi esemplificativi del moto periodo procedendo quindi verso lo studio delle cosiddette «oscillazioni» e delle grandezze fisiche le caratterizzano e che sono propedeutiche allo studio dei fenomeni ondulatori 2

Altri esempi di moto periodico che ci sono familiari • Il moto del pendolo 3

• La vibrazione di una corda di violino 4

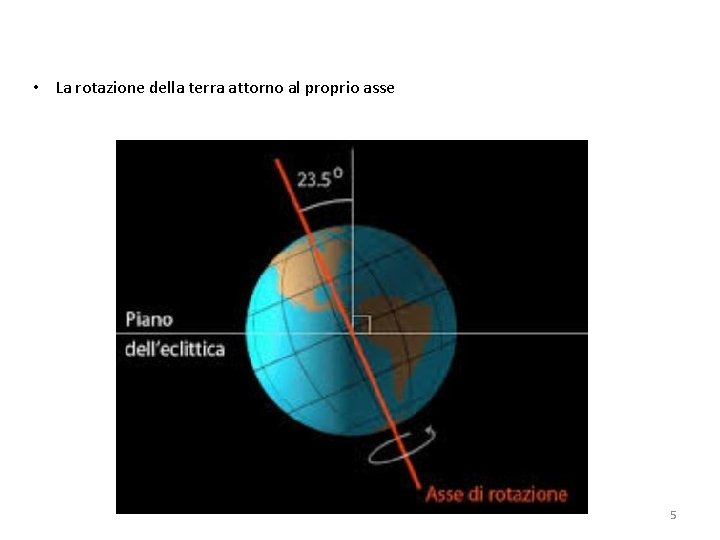
• La rotazione della terra attorno al proprio asse 5

• Il moto circolare uniforme 6

• Il moto di una massa attaccata ad una molla 7

Nella realtà, molti dei moti periodici a noi noti sono solo approssimativamente periodici a causa dell’azione delle forze d’attrito che dissipano l’energia del moto • Il pendolo smette gradualmente di oscillare • La corda di violino smette di vibrare • Etc… In questi casi il moto viene detto moto periodico smorzato Nel moto periodico ne la velocità ne l’accelerazione sono costanti (Nel caso del moto circolare uniforme lo sono ma solo in modulo) 8

• Se il moto va avanti e indietro lungo lo stesso percorso, viene detto: Moto oscillatorio o vibratorio • Un ciclo completo del moto si chiama oscillazione o vibrazione • Il tempo speso per effettuare una oscillazione completa è denominato Periodo T • La frequenza • Quindi: f è il numero di oscillazioni che occorrono nell’unità di tempo f = 1/T • La posizione in cui nessuna forza agisce sul corpo è denominata posizione di equilibrio • L’elongazione (lineare o angolare) è la distanza (lineare o angolare) dalla posizione di equilibrio ad ogni istante • L’ampiezza A del moto è l’elongazione massima 9

L’oscillatore armonico Se una particella vibra (oscilla) attorno ad una posizione di equilibrio sotto l’azione di una forza proporzionale alla elongazione, il suo moto viene detto armonico Questa forza di richiamo è sempre diretta verso la posizione di equilibrio e dà origine al tipo più semplice di moto armonico L’esempio classico di oscillatore armonico lo abbiamo già visitato ed è costituito da una massa m legata ad una molla priva di massa e di costante elastica k, disposta su un piano senza attrito. Supponendo che il moto avvenga lungo x e che la posizione di riposo coincida con l’origine O, quando la massa di trova su un punto di coordinata x la forza esercitata su d essa dalla mola è data dalla: F = −kx 10

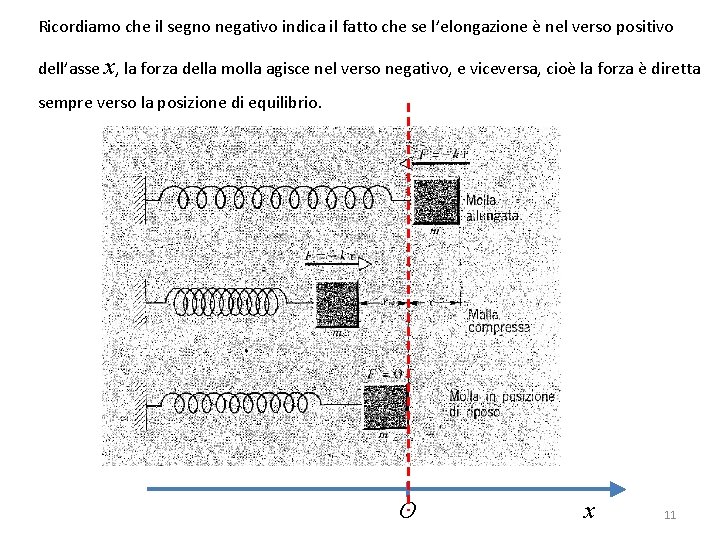
Ricordiamo che il segno negativo indica il fatto che se l’elongazione è nel verso positivo dell’asse x, la forza della molla agisce nel verso negativo, e viceversa, cioè la forza è diretta sempre verso la posizione di equilibrio. O x 11

12

13

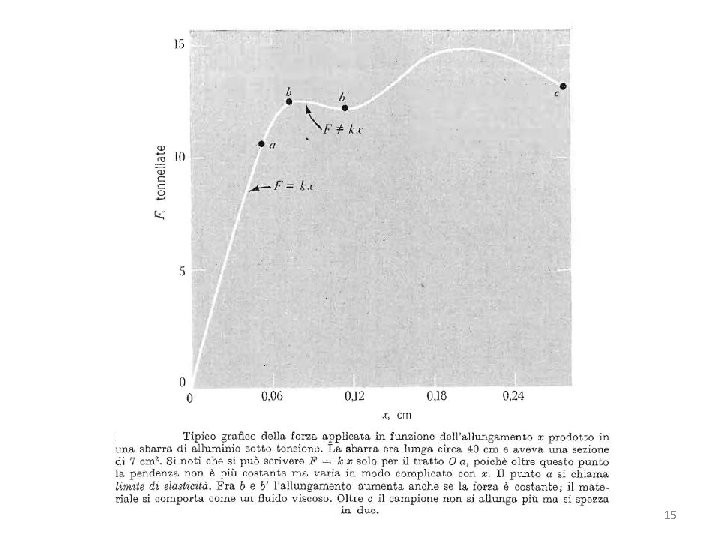
La legge di Hooke ha una sua formulazione generale, di cui il caso della molla è semplicemente un caso particolare: Hooke: Quando un solido viene deformato, esso si oppone alla deformazione con una forza proporzionale all’entità della deformazione stessa, purché questa non sia troppo grande. Quando questo limite (che dipende dalle caratteristiche di elasticità del solido) viene superato, si passa dal comportamento elastico al comportamento plastico: un corpo che subisce una deformazione elastica tende a riacquisire la sua forma, un corpo che subisce una deformazione plastica, rimane deformato. Se su un corpo soggetto a deformazione plastica continua ad insistere una forza esterna superiore ad un certo limite, il corpo può andare incontro alla frattura definitiva. 14

15

Nel caso unidimensionale, la Legge di Hooke si riduce come abbiamo già visto, alla semplice formula che abbiamo già visitato: F = −k x dove abbiamo visto che: • x rappresenta la deformazione, cioè l’allungamento o la compressione rispetto alla posizione non deformata. • F è la resistenza offerta dal solido • k è la costante elastica del solido • Il segno negativo tiene conto del fatto che F si oppone alla deformazione 16

Pertanto, un solido deformato elasticamente possiede una certa energia potenziale U data dalla relazione: U = ½ k x 2 Per il solido non deformato (x = 0) l’energia potenziale è minima e quindi x = 0 è una posizione di equilibrio stabile 17

La forza di richiamo e l’energia potenziale di un corpo elastico e di un oscillatore armonico sono esattamente le stesse (finché siamo nel limite di elasticità). Quindi un solido deformato elasticamente comincerà a vibrare esattamente come l’oscillatore armonico. Le corde vibranti, le vibrazioni sonore, per le oscillazioni elettriche, manifestano lo stesso moto armonico e cioè sono descritte tutte dalle stesse equazioni dell’oscillatore armonico. Nel caso esemplificativo del moto armonico, e cioè l’oscillatore armonico, k è la costante di elasticità della molla; in altri sistemi oscillanti k potrà essere connessa ad altre caratteristiche del sistema in esame, che vanno analizzate caso per caso. L’oscillatore armonico (cioè il sistema massa-molla) costituisce il nostro prototipo per lo studio del moto armonico 18

Il moto armonico 19

20

E’ interessante notare che una funzione coseno scritta in questa forma generale: A cos (ωt + δ) rappresenta di fatto una generica combinazione lineare di funzioni seno e coseno e rappresenta quindi una soluzione del tutto generale. Infatti: cos (θ + δ) = cos δ cos θ − sin δ sin θ = a cos θ + b sin θ Generica combinazione lineare di funzioni seno e coseno 21

22

23

Vediamo adesso di capire il significato fisico della costante ω : Se nella funzione x (t) = A cos (ωt + δ) il tempo t aumenta della quantità Δ t = 2π / ω si ha: x (t) = A cos (ωt + δ) x (t) = A cos (ω[t + 2π / ω] + δ) = A cos (ωt + 2π + δ) = A cos (ωt + δ) Cioè: la funzione si ripete identica dopo un tempo pari a 2π Cioè: 2π / ω è il periodo T di ripetizione del moto, /ω e poiché si era posto ω2 = k/m si ha: T = 2π / ω = 2π √(m / k) 24

25

La quantità ω = 2π / T è denominata frequenza angolare (o pulsazione) e ha le dimensioni di una velocità angolare, quindi la sua unità di misura è il radiante/sec La quantità A nella funzione x (t) = A cos (ωt + δ) ha un semplice significato fisico: la funzione coseno assume valori fra − 1 e 1. Quindi l’elongazione x ha il suo valore massimo proprio nel valore A. Cioè A è l’ampiezza del moto e poiché A non è determinata dalla equazione differenziale, né dai parametri del sistema (m e k), ma solo dalle condizioni Inziali, un dato oscillatore puo oscillare con varie ampiezze. Cioè: il periodo di oscillazione di un oscillatore armonico non dipende dalla ampiezza del moto 26

La quantità (ωt + δ) è denominata fase del moto. La costante δ è la costante di fase Due moti di un dato oscillatore possono avere la stessa ampiezza e frequenza e costante di fase differente, che dipenda dalla elongazione iniziale. QUINDI in un oscillatore armonico: Il periodo di ripetizione è determinato dai parametri dell’oscillatore (m e k) L’ampiezza e la costante di fase del moto sono determinate dalle condizioni inziali della particella oscillante (ampiezza dell’elongazione inziale e velocità iniziale) 27

28

Considerazioni energetiche L’oscillatore armonico è un sistema conservativo in quanto la forza in gioco è solo funzione della posizione: F = −k x U = ½ k x 2 e risulta pertanto F = − d. U / dx In assenza di forze dissipative, l’energia meccanica si conserva. Naturalmente sia l’energia cinetica K che l’energia potenziale U variano continuamente durante l’oscillazione, ma la loro somma si conserva come dimostreremo di seguito. 29

30

L’energia potenziale U ad ogni istante vale ½ k x 2 e poiché x (t) = A cos (ωt + δ) si ha: U = ½ k A 2 cos 2 (ωt + δ) Quindi: L’energia potenziale varia nel tempo con andamento pari al quadrato del coseno e ha come valore massimo ½ k A 2 Cioè: Kmax = Umax = ½ k A 2 Ci aspettiamo quindi: E Infatti: = K + U = ½ k A 2 E = K + U = ½ k A 2 sin 2 (ωt + δ) + ½ k A 2 cos 2 (ωt + δ) E = K + U = ½ k A 2 [sin 2 (ωt + δ) + cos 2 (ωt + δ)] E = K + U = ½ k A 2 31

Il risultato è quindi che: E = K + U = ½ m v 2 + ½ k x 2 = ½ k A 2 L’energia meccanica totale di una particella in moto armonico è proporzionale al quadrato dell’ampiezza del moto 32

Alcune applicazioni del moto armonico 33

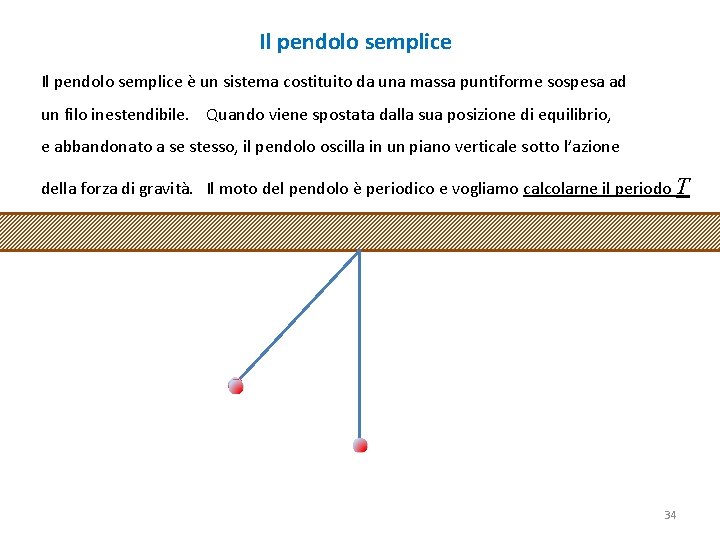
Il pendolo semplice è un sistema costituito da una massa puntiforme sospesa ad un filo inestendibile. Quando viene spostata dalla sua posizione di equilibrio, e abbandonato a se stesso, il pendolo oscilla in un piano verticale sotto l’azione della forza di gravità. Il moto del pendolo è periodico e vogliamo calcolarne il periodo T 34

Riconsideriamo la geometria del sistema e definiamo gli assi di riferimento e le forze in gioco. La massa vale m e il filo di lunghezza l forma un angolo θ con la verticale. Le forze che agiscono sulla massa m sono la forza di gravità mg diretta in verticale verso il basso e T, la tensione del filo. Scegliamo una coppia di assi cartesiani diretti uno verso il raggio e uno verso la tangente al cerchio su cui si muove la massa. Scomponiamo mg in una componente radiale mg cos θ e una componente tangenziale mg sin θ 35

La componente radiale e la tensione del filo istante per istante sono uguali e contrarie e infatti non c’è moto della massa m in senso radiale. La componente tangenziale è la forza di richiamo esercitata su m tendente e ricondurla alla sua posizione di equilibrio. La forza di richiamo pertanto è: F = −m g sin θ NOTA: la forza F non è proporzionale allo spostamento angolare θ ma a sin θ Il moto che ne risulta quindi NON è armonico Tuttavia, se θ è piccolo sin lungo l’arco di cerchio è x θ ≈ θ , dove θ =lθ è espresso in radianti. Lo spostamento e per piccoli angoli il moto è praticamente rettilineo 36

37

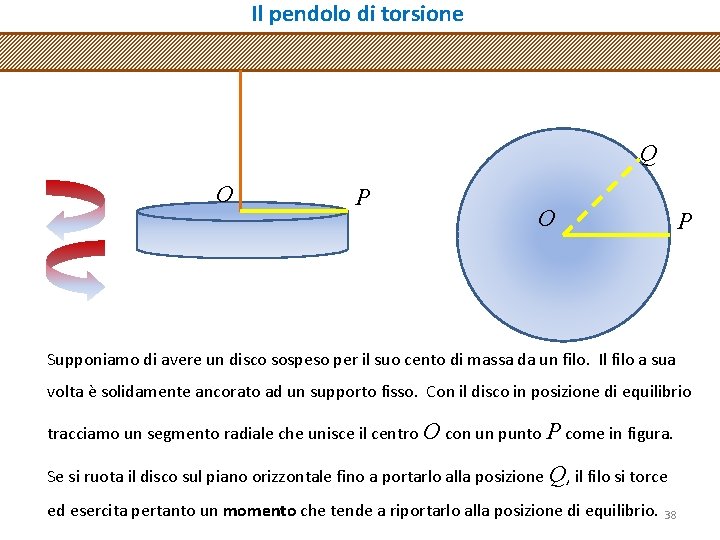
Il pendolo di torsione Q O P Supponiamo di avere un disco sospeso per il suo cento di massa da un filo. Il filo a sua volta è solidamente ancorato ad un supporto fisso. Con il disco in posizione di equilibrio tracciamo un segmento radiale che unisce il centro O con un punto P come in figura. Se si ruota il disco sul piano orizzontale fino a portarlo alla posizione Q, il filo si torce ed esercita pertanto un momento che tende a riportarlo alla posizione di equilibrio. 38

39

40

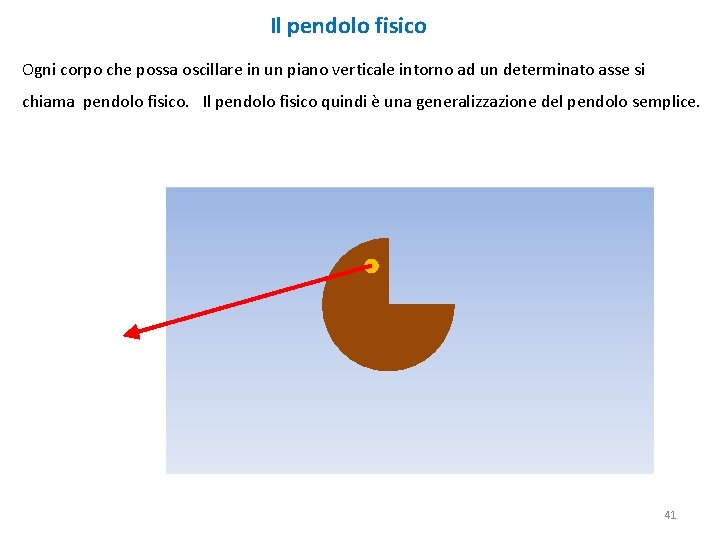
Il pendolo fisico Ogni corpo che possa oscillare in un piano verticale intorno ad un determinato asse si chiama pendolo fisico. Il pendolo fisico quindi è una generalizzazione del pendolo semplice. 41

Indichiamo con m la massa del corpo, con P il punto dove passa l’asse di rotazione, con C il suo centro di massa e con I il suo momento di inerzia rispetto a P. Sia r il raggio vettore P-C. Supponiamo di spostare il corpo di un angolo θ dalla sua posizione di equilibrio (che è quella in cui il centro di massa C giace sulla verticale passante per P). P θ r C −m g Il momento della forza di gravità mg sarà τ = −mg r sin θ 42

43

II Parte 44

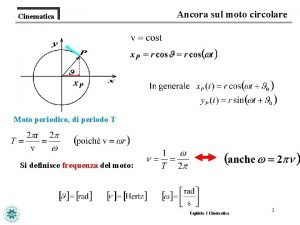
Relazione fra il moto armonico e il moto circolare uniforme Vedremo adesso che c’è una interessante relazione fra il moto armonico rettilineo e il moto circolare uniforme. Inoltre, il moto circolare uniforme è anche l’esempio di una composizione di moti armonici semplici, un fenomeno che incontreremo spesso nello studio delle onde. 45

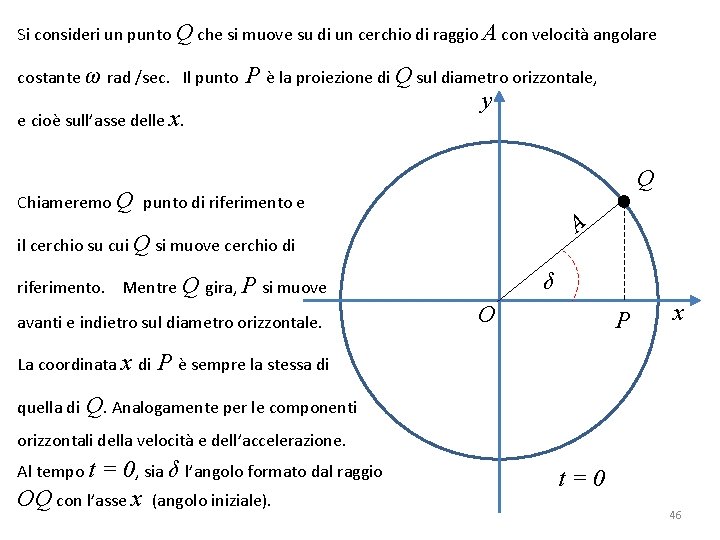
Si consideri un punto Q che si muove su di un cerchio di raggio A con velocità angolare costante ω rad /sec. Il punto e cioè sull’asse delle x. P è la proiezione di Q sul diametro orizzontale, y Q Chiameremo Q punto di riferimento e A il cerchio su cui Q si muove cerchio di riferimento. Mentre avanti e indietro sul diametro orizzontale. La coordinata x di quella di δ Q gira, P si muove O P x P è sempre la stessa di Q. Analogamente per le componenti orizzontali della velocità e dell’accelerazione. Al tempo t = 0, sia δ l’angolo formato dal raggio OQ con l’asse x (angolo iniziale). t=0 46

Poiché la velocità angolare ω è costante, ad ogni istante di tempo successivo, l’angolo fra il raggio OQ e l’asse delle x sarà dato da ωt +δ y Pertanto, ad ogni istante la coordinata x di Q (e x = A cos (ωt + δ) P) sarà: Q A ωt + δ Quindi il punto P si muove di moto armonico P x O Cioè: il moto armonico può essere considerato come la proiezione di un moto circolare uniforme su di un diametro. t > 0 47

A seguito di questa definizione del moto armonico riferito al moto circolare uniforme si ha: • La ω di un moto armonico è la velocità angolare del punto di riferimento • La frequenza del moto armonico equivale al numero di rivoluzioni nell’unità di tempo del punto di riferimento • Quindi f = ω / 2π, e di conseguenza ω = 2π f • Il tempo impiegato dal punto di riferimento a compiere una rivoluzione completa equivale al periodo T del moto armonico. • Quindi T = 2π / ω ossia ω = 2π / T • L’ampiezza del moto armonico equivale al raggio del cerchio di riferimento • La fase ωt + δ del moto armonico corrisponde all’angolo formato dal raggio rotante nel cerchio di riferimento 48

Se avessimo considerato la proiezione y invece che la proiezione x avremmo ottenuto il seguente risultato: y = A sin (ωt + δ) Si tratta nuovamente di moto armonico, che differisce dal precedente soltanto per la fase iniziale δ − π/2 E infatti il moto armonico può essere ottenuto come proiezione su un qualunque diametro del moto sul cerchio del punto di riferimento Q. Inversamente, il moto circolare uniforme può essere ottenuto come combinazione di due moti armonici 49

Composizione di moti armonici Vediamo allora il caso più generale di moti risultanti dalla combinazione di moti armonici ortogonali. In fisica occorre di frequente il caso in cui un moto sia la combinazione di due moti armonici rettilinei fra loro ortogonali, cioè la somma di due oscillazioni indipendenti Ci soffermeremo adesso sul caso in cui le frequenze delle due vibrazioni sono le stesse: x = Ax cos (ωt + δx) y = Ay cos (ωt + δy) Le due relazioni indicano due moti armonici ortogonali (uno lungo x e uno lungo y) aventi la stessa frequenza angolare ω ma diversa ampiezza e fase 50

51

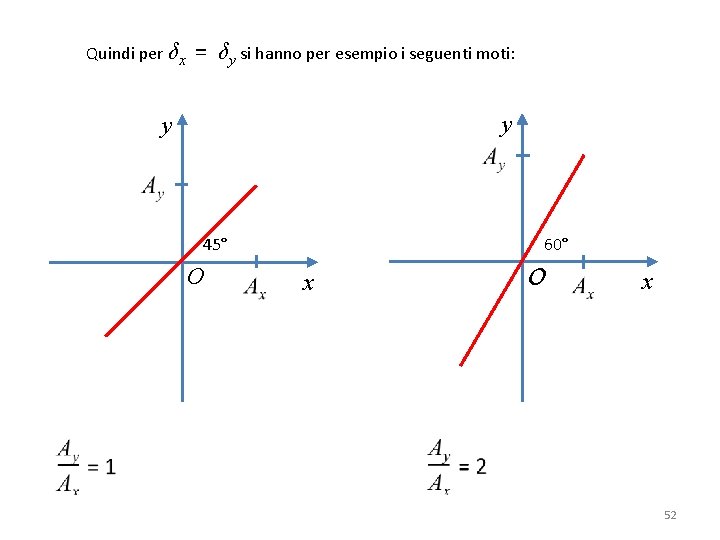
Quindi per δx = δy si hanno per esempio i seguenti moti: y y 45° O 60° O x x 52

53

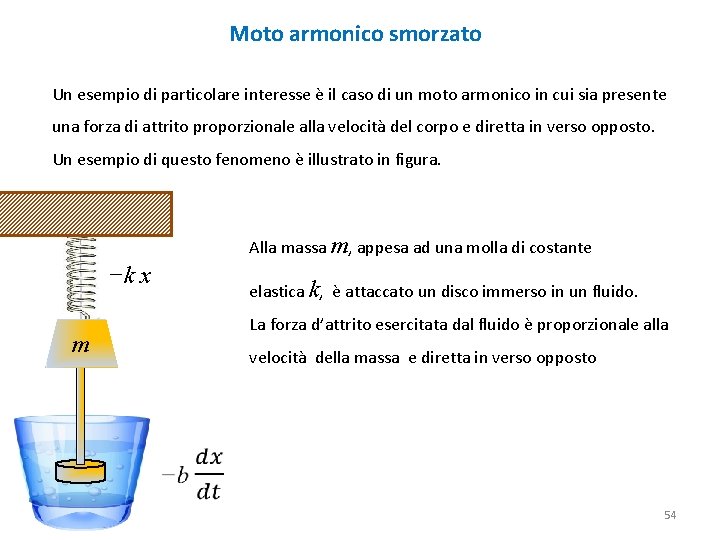
Moto armonico smorzato Un esempio di particolare interesse è il caso di un moto armonico in cui sia presente una forza di attrito proporzionale alla velocità del corpo e diretta in verso opposto. Un esempio di questo fenomeno è illustrato in figura. Alla massa m, appesa ad una molla di costante −k x elastica k, è attaccato un disco immerso in un fluido. La forza d’attrito esercitata dal fluido è proporzionale alla m velocità della massa e diretta in verso opposto 54

55

56

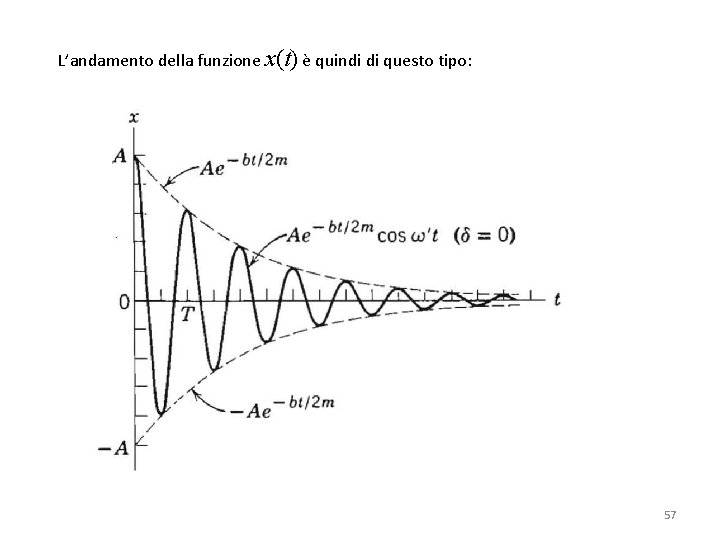
L’andamento della funzione x(t) è quindi di questo tipo: 57

Oscillazioni forzate e risonanza 58

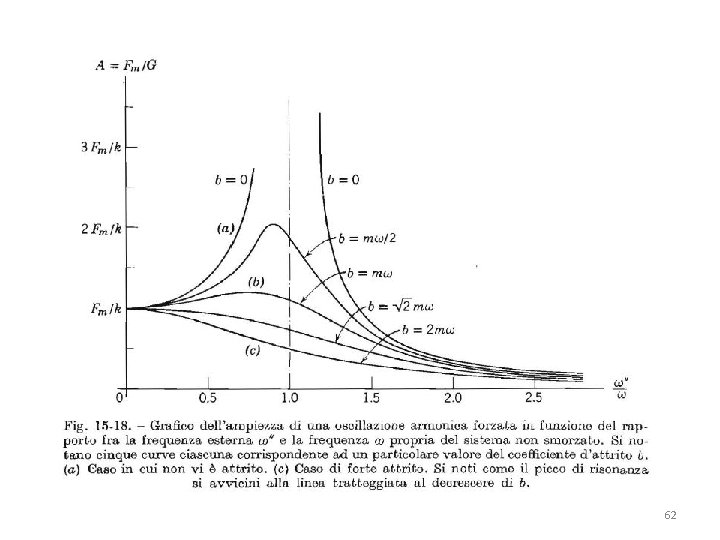
Non c’è però alcun dubbio che noi possiamo forzare un sistema elastico a oscillare applicandogli una forza esterna periodica. In questo caso il corpo oscilla alla frequenza della forza e non alla sua frequenza naturale. In questo caso si parla di oscillazioni forzate. Tuttavia, la «risposta» del sistema a queste sollecitazioni dipende dalla relazione fra la frequenza della forza esterna e la frequenza naturale del sistema. In particolare vedremo che tanto più la frequenza della forza esterna è vicina alla frequenza naturale, tanto più ampie saranno le oscillazioni. 59

60

61

62

Esercizi ed esempi 63

Esempio 1 Una molla disposta in orizzontale è allungata di 3 cm quando su di essa agisce una forza di 9 nt. A questa molla viene attaccata una massa m=1 kg. La massa, allontanata di 4 cm dalla posizione di equilibrio lungo un tavolo privo di attrito viene quindi lasciata libera di compiere oscillazioni armoniche. Quesito-1: Quanto vale la costante elastica della molla ? Quesito-2: Quanto vale la forze esercitata sulla massa da 1 kg appena prima che questa venga abbandonata ? Quesito-3: Quale è il periodo dell’oscillazione ? Quesito-4: Quale è l’ampiezza A del moto ? Quesito-5: Quale è l’a velocità massima della massa oscillante ? Quesito-6: Quale è l’accelerazione massima? 64

Una molla disposta in orizzontale è allungata di 3 cm quando su di essa agisce una forza di 9 nt. A questa molla viene attaccata una massa m=1 kg. La massa, allontanata di 4 cm dalla posizione di equilibrio lungo un tavolo privo di attrito viene quindi lasciata libera di compiere oscillazioni armoniche. Quesito-1: Quanto vale la costante elastica della molla ? Dalla relazione: F = −k x, risulta: k = F/x Quindi: k = 9 nt / 0. 03 = 300 nt/m 65

Una molla disposta in orizzontale è allungata di 3 cm quando su di essa agisce una forza di 9 nt. A questa molla viene attaccata una massa m=1 kg. La massa, allontanata di 4 cm dalla posizione di equilibrio lungo un tavolo privo di attrito viene quindi lasciata libera di compiere oscillazioni armoniche. Quesito 2: Quanto vale la forza esercitata sulla massa da 1 kg appena prima che questa venga abbandonata ? La massa era stata allontanata di 4 cm dalla posizione di riposo, quindi: F = −k x = -300 nt/m x 0. 04 m = − 12 nt 66

Una molla disposta in orizzontale è allungata di 3 cm quando su di essa agisce una forza di 9 nt. A questa molla viene attaccata una massa m=1 kg. La massa, allontanata di 4 cm dalla posizione di equilibrio lungo un tavolo privo di attrito viene quindi lasciata libera di compiere oscillazioni armoniche. 67

Una molla disposta in orizzontale è allungata di 3 cm quando su di essa agisce una forza di 9 nt. A questa molla viene attaccata una massa m=1 kg. La massa, allontanata di 4 cm dalla posizione di equilibrio lungo un tavolo privo di attrito viene quindi lasciata libera di compiere oscillazioni armoniche. Quesito 4: Quale è l’ampiezza A del moto ? Abbiamo visto che l’ampiezza A è semplicemente l’elongazione iniziale: 4 cm !! 68

Una molla disposta in orizzontale è allungata di 3 cm quando su di essa agisce una forza di 9 nt. A questa molla viene attaccata una massa m=1 kg. La massa, allontanata di 4 cm dalla posizione di equilibrio lungo un tavolo privo di attrito viene quindi lasciata libera di compiere oscillazioni armoniche. 69

70

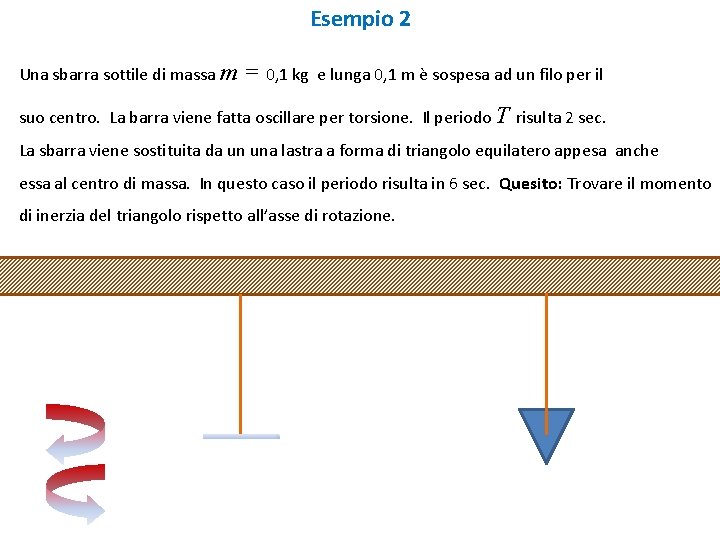
Esempio 2 Una sbarra sottile di massa m = 0, 1 kg e lunga 0, 1 m è sospesa ad un filo per il suo centro. La barra viene fatta oscillare per torsione. Il periodo T risulta 2 sec. La sbarra viene sostituita da un una lastra a forma di triangolo equilatero appesa anche essa al centro di massa. In questo caso il periodo risulta in 6 sec. Quesito: Trovare il momento di inerzia del triangolo rispetto all’asse di rotazione.

Si ah quindi: Isbarra = m l 2 /12 = (0, 1 x 0, 12 ) /12 = 0, 001/12 = 8, 33 x 10− 5 kg-m 2 72

73

Esempio 3 74