OSCILLATIONS Chapter 15 Simple Harmonic Motion SHM Systems

OSCILLATIONS Chapter 15

Simple Harmonic Motion (SHM) Systems

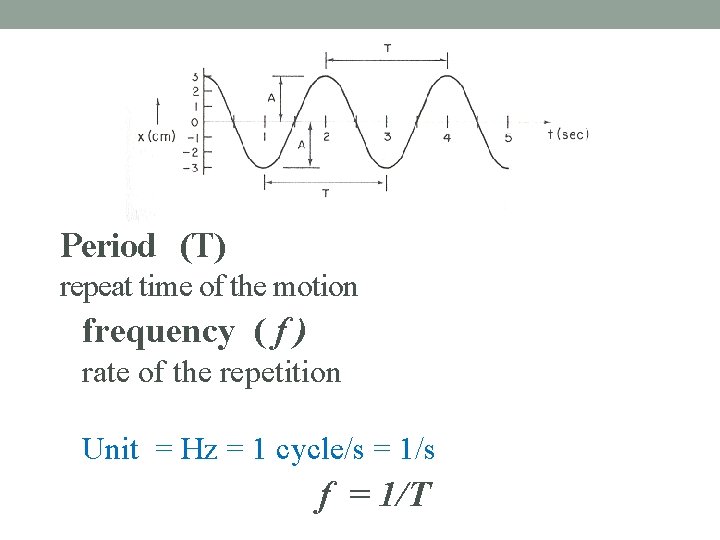
Period (T) repeat time of the motion frequency ( f ) rate of the repetition Unit = Hz = 1 cycle/s = 1/s f = 1/T

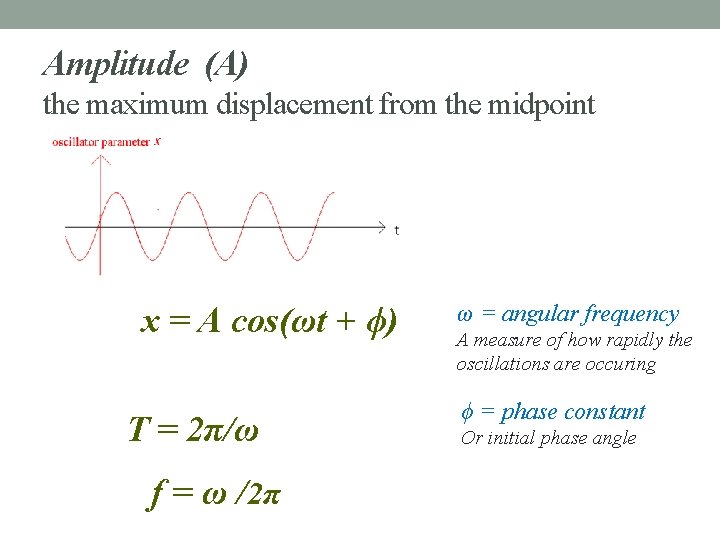
Amplitude (A) the maximum displacement from the midpoint x = A cos(ωt + ϕ) T = 2π/ω f = ω /2π ω = angular frequency A measure of how rapidly the oscillations are occuring ϕ = phase constant Or initial phase angle

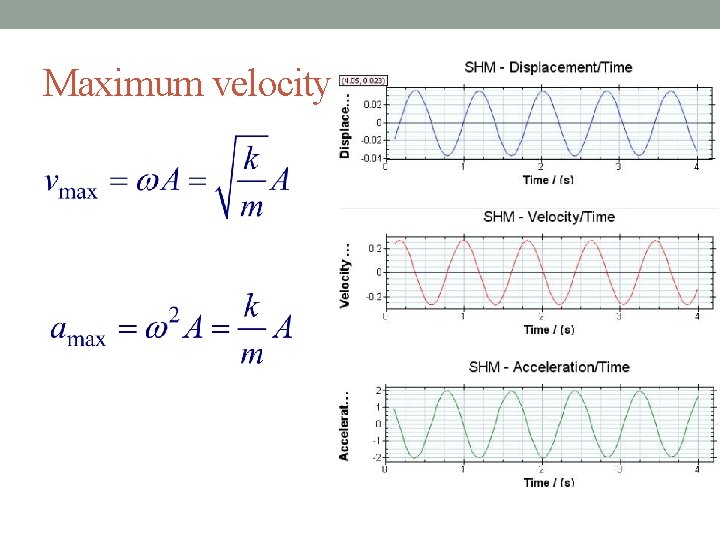
Maximum velocity

Here’s a way of thinking about simple harmonic motion that will be very useful later. Suppose a particle is in uniform circular motion on a circle of radius A and with angular speed T. The projection of that motion onto any axis is a point moving in simple harmonic motion with amplitude A and circular frequency T.

A particle oscillates with simple harmonic motion, so that its displacement varies according to the expression x = (5 cm)cos(2 t + π/6) where x is in centimeters and t is in seconds. At t = 0 find (a) the displacement of the particle, (b) its velocity, and (c) its acceleration. (d) Find the period and amplitude of the motion.

A 200 -g block connected to a light spring for which the force constant is 5. 00 M/m is free to oscillate on a horizontal frictionless surface. The block is displaced 5. 00 cm from equilibrium and released from rest. Determine the maximum speed. What is the maximum acceleration? Express the position, velocity, and acceleration as functions of time.

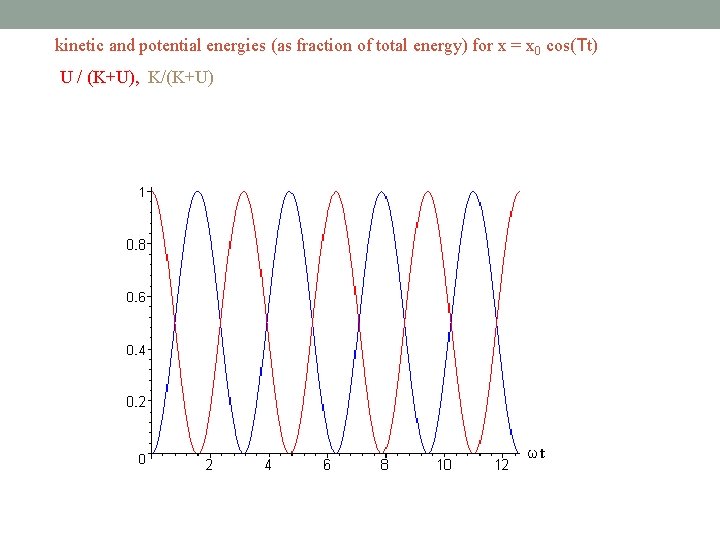
The total energy of a simple harmonic oscillator is constant in time and proportional to the square of the amplitude

kinetic and potential energies (as fraction of total energy) for x = x 0 cos(Tt) U / (K+U), K/(K+U)

The frequency of a resonator is determined by the way energy shifts back and forth between kinetic and potential terms.

These are called sinusoidal oscillations, or simple harmonic motion.

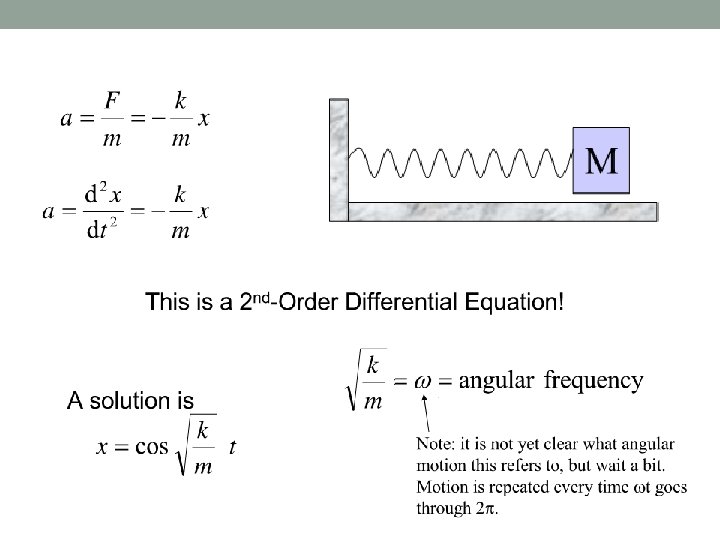
For a mass-and-spring system, the motion is simple harmonic at an angular frequency of The motion is always simple harmonic whenever the restoring force is a linear function of the oscillation parameter. Another way to say this is that the motion is simple harmonic whenever the potential energy is a quadratic function of the oscillation parameter.

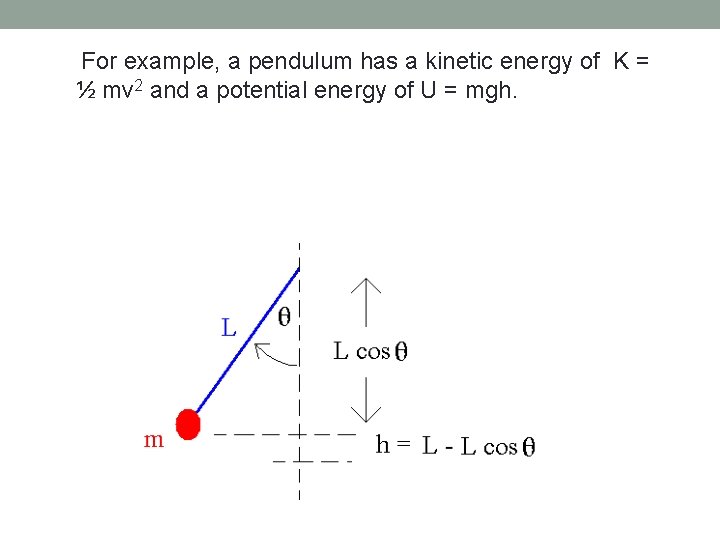
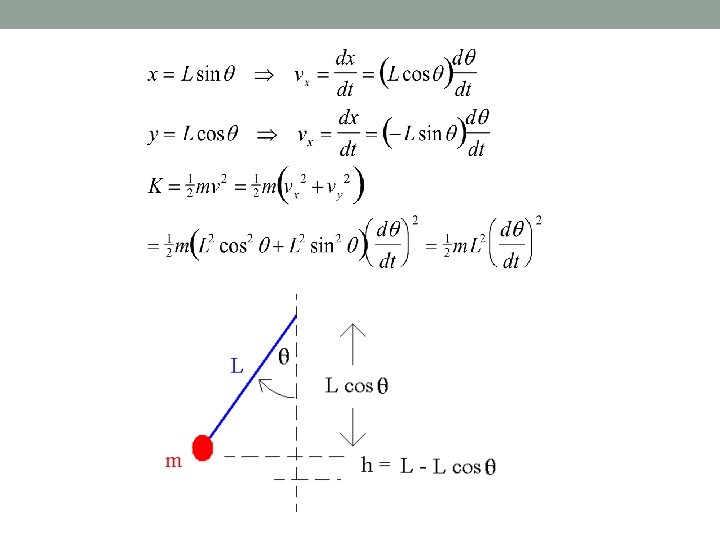
For example, a pendulum has a kinetic energy of K = ½ mv 2 and a potential energy of U = mgh.

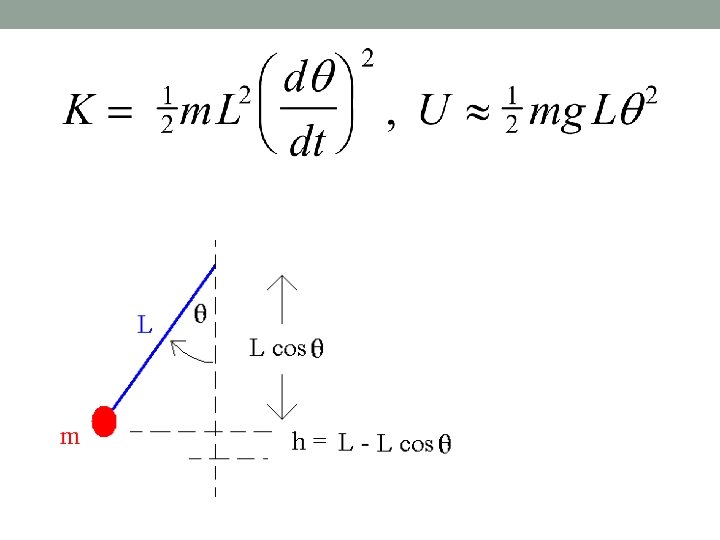
K = ½ m L 2 (dθ/dt)2 , U = ½ mg. L θ 2 Compare to K = ½ m (dx/dt)2, U = ½ kx 2 The circular frequency of the mass-spring system is (½ k / ½ m)1/2 = ( k / m)1/2 By analogy, the circular frequency of the pendulum is [½ mg. L / ½ m L 2]1/2 = [g / L]1/2