Oscillations and Waves Wave Properties Reflection and Refraction

$Reflection and Refraction Terminology (define these in your own words) - Incident ray -$

$Refraction This is caused by a change in speed as a wave passes form$

$Refractive index The degree of refraction of light at a boundary is measured by$

Snell’s Law i Material 1 Material 2 r It can be shown that the

$In the data booklet the angles of incidence and refraction are called θ 1$

E. g. 1 A wave travelling at 12 cms-1 is incident upon a surface

E. g. 2 For light travelling from water into glass, r=20°. If nw =

Phase and Wavefronts If two oscillating bodies are in phase, this means that they

$Diffraction When a wave passes through a gap or edge of a barrier they$

Superposition (interference) Whenever two waves of the same type meet at the same point,

For constructive interference at any point, wavefronts must be ‘in phase’ and their path

Task: i. On your interference diagram… Draw in lines of constructive and destructive interference

Coherent waves A stable pattern of interference is only obtained if the two wave

Superposition links - Phe. T Sound (see jar file) - Superposition of two pulses

Slides: 25

Download presentation

Oscillations and Waves Wave Properties

$Reflection and Refraction Terminology (define these in your own words) - Incident ray -$

Reflection and Refraction Terminology (define these in your own words) - Incident ray - Reflected ray - Refracted ray - Normal line - Angle of incidence / reflection / refraction - Interface or boundary Law of reflection angle of incidence = angle of reflection

$Refraction This is caused by a change in speed as a wave passes form$

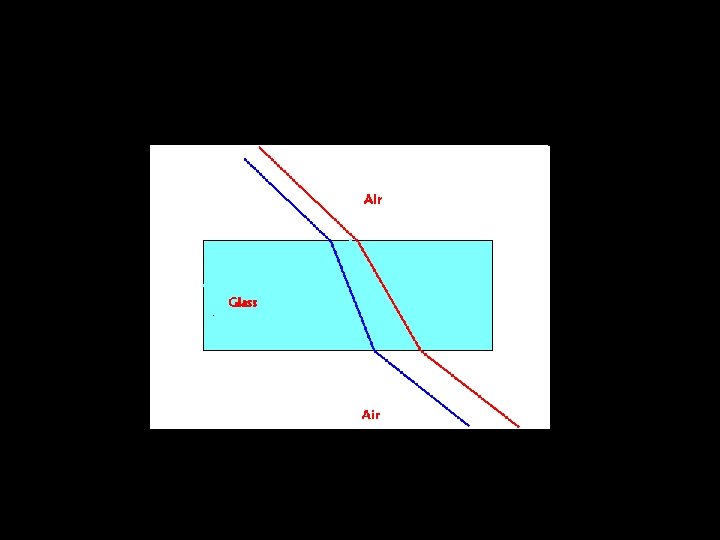
Refraction This is caused by a change in speed as a wave passes form one medium into another. It results in… - change in direction - change in wavelength ( as v = fλ ) When there is refraction of a wave such as light, part of the wave is also reflected. This results in a decrease in intensity of the transmitted (refracted) wave.

$Refractive index The degree of refraction of light at a boundary is measured by$

Refractive index The degree of refraction of light at a boundary is measured by the refractive index, n. The greater the reduction in speed of the light, the greater the refractive index: nm = c vm nm = absolute refractive index of a medium, m (no unit) c = speed of light in a vacuum vm = speed of light in medium Experiment: Investigate the relationship between the angle of incidence and angle of refraction for light.

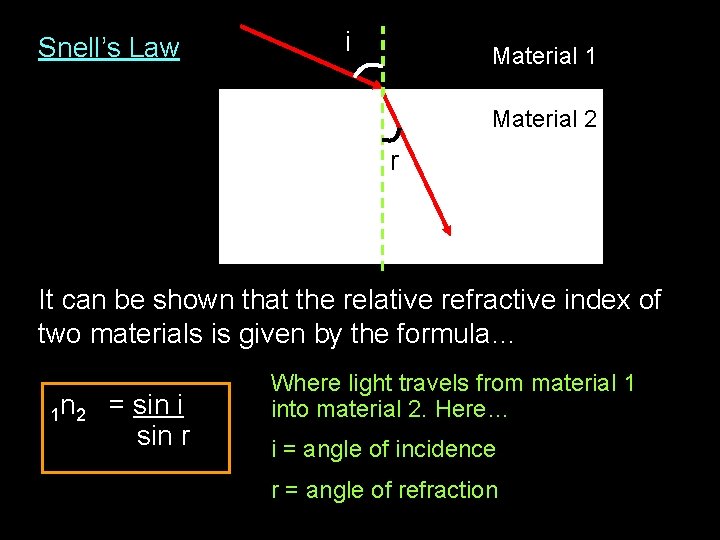
Snell’s Law i Material 1 Material 2 r It can be shown that the relative refractive index of two materials is given by the formula… 1 n 2 = sin i sin r Where light travels from material 1 into material 2. Here… i = angle of incidence r = angle of refraction

$In the data booklet the angles of incidence and refraction are called θ 1$

In the data booklet the angles of incidence and refraction are called θ 1 and θ 2. It can further be shown that… 1 n 2 = sinθ 1 = v 1 = n 2 sinθ 2 v 2 n 1 Note that this is written in the data booklet as… sinθ 2 = v 2 sinθ 1 v 1 = n 1 n 2

E. g. 1 A wave travelling at 12 cms-1 is incident upon a surface at an angle of 55° from the normal. a. If the angle of refraction is 40°, determine the speed of the wave in the second medium. sinθ 2 = v 2 sinθ 1 v 1 sin 40 = v 2 sin 55 12 v 2 = 9. 4 cms-1 b. If the initial wavelength is 6 cm determine the frequency of the wave in the second medium. In first medium: v = fλ f = v/λ = 0. 12 / 0. 06 = 2. 0 Hz Frequency does not change during refraction f = 2. 0 Hz

E. g. 2 For light travelling from water into glass, r=20°. If nw = 1. 33 and ng = 1. 50, determine i (θ 1). sinθ 2 = n 1 sinθ 1 n 2 sin 20 = 1. 33 sinθ 1 1. 50 sinθ 1 = 0. 34 / 0. 89 = 0. 38 θ 1 = sin-1 0. 38 = 22. 5°

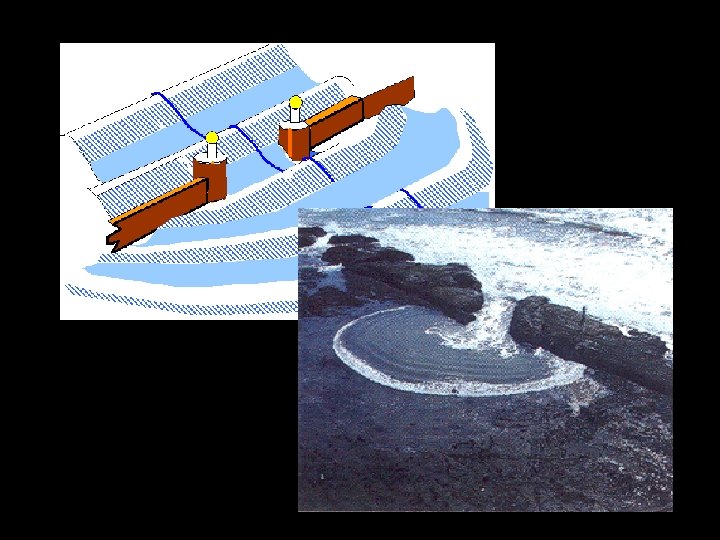
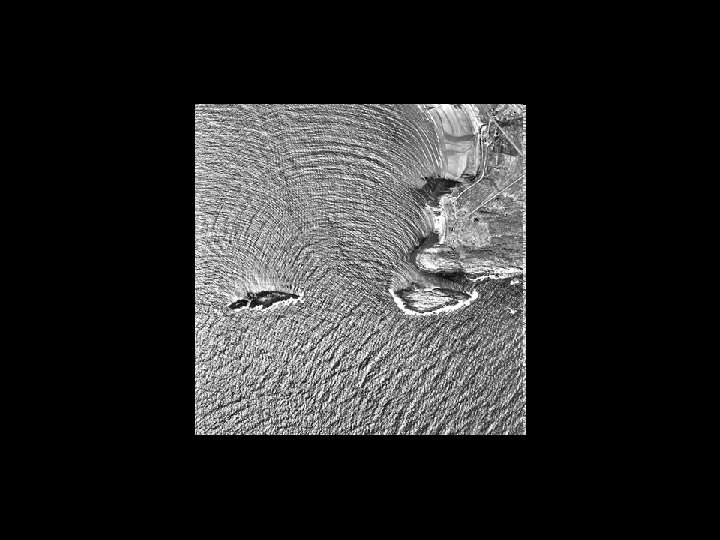
Phase and Wavefronts If two oscillating bodies are in phase, this means that they reach their maximum displacement at the same time. E. g. any two wave crests are in phase. A wavefront is a line joining adjacent points that are in phase. E. g. During refraction of a water wave: (Youtube link)

$Diffraction When a wave passes through a gap or edge of a barrier they$

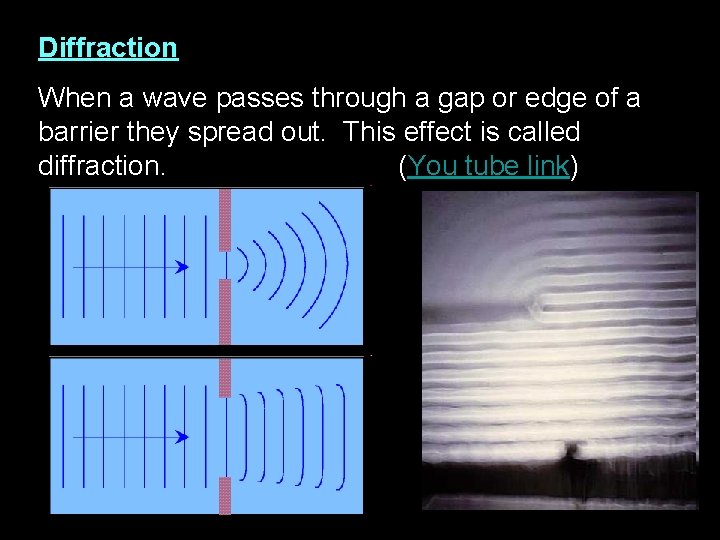
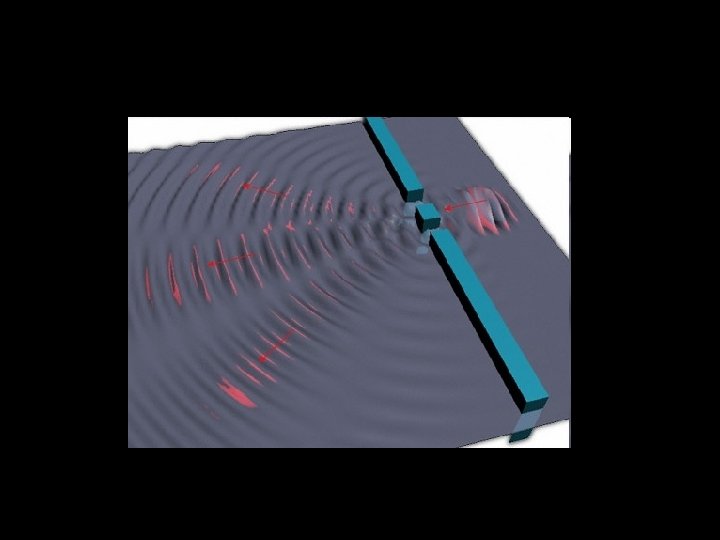
Diffraction When a wave passes through a gap or edge of a barrier they spread out. This effect is called diffraction. (You tube link)

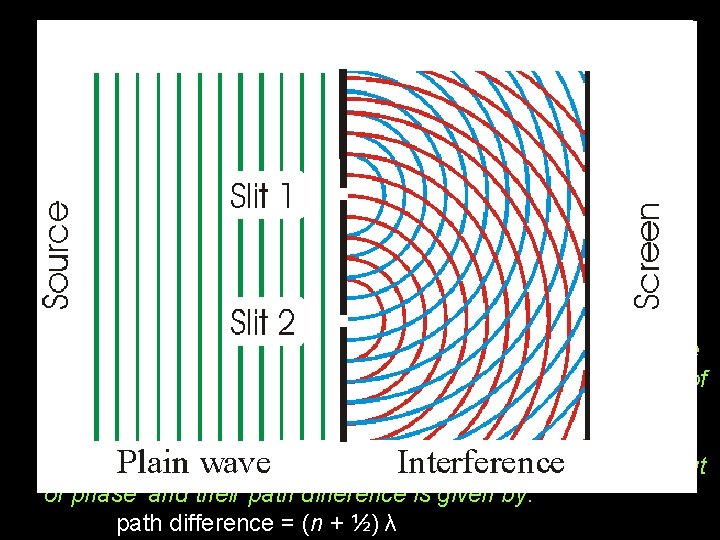
Superposition (interference) Whenever two waves of the same type meet at the same point, the total amplitude (displacement) at that point equals the sum of the amplitudes (displacements) of the individual waves. (You tube link 1 and link 2)

For constructive interference at any point, wavefronts must be ‘in phase’ and their path difference must be a whole number of wavelengths: path difference = nλ For destructive interference at any point, wavefronts are ‘π out of phase’ and their path difference is given by: path difference = (n + ½) λ

Task: i. On your interference diagram… Draw in lines of constructive and destructive interference ii. Indicate the lines that join points… a. in phase b. 2π out of phase (path difference = λ) c. 4π out of phase (path difference = 2λ) d. 3π out of phase (path difference = 1. 5λ)

Coherent waves A stable pattern of interference is only obtained if the two wave sources are coherent. Two coherent wave sources… i. have a constant phase difference, ii. thus produce waves with equal frequency.

Superposition links - Phe. T Sound (see jar file) - Superposition of two pulses - With editable wave equations - Creating a standing wave

Subtitle Text