Oscillations and Waves An oscillation is a repetitive

Oscillations and Waves An oscillation is a repetitive motion back and forth around a central point which is usually an equilibrium position. A special type of oscillation is called Simple Harmonic Motion (SHM). This type of oscillation is for a mass moving around a point of equilibrium which serves as the reference point for displacement (DISTANCE FROM EQUILIBRIUM). To be simple harmonic motion, the motion MUST be produced by a force that increases LINEARLY with respect to displacement but in the opposite direction. For all SHM: F=-kx =ma F = restoring force k is a constant value ( usually the spring constant) x = displacement from equilibrium The k does not HAVE to be a spring constant; it simply needs to be a constant value.

The motion of the mass is a result of the conservation of energy while the mass moves. Usually there is an exchange of energy between elastic potential energy and kinetic energy. The POTENTIAL energy of the oscillator is: US = ½ k x 2 ( The energy stored in the elastic medium ) The KINETIC energy of the oscillator is: K = ½ m v 2 The TOTAL energy of the oscillator remains constant: ETot = K + US = ½ m v 2 + ½ k x 2 As the mass moves to either side of equilibrium, it will stretch or compress or the spring. The spring gains potential energy. Whenever the spring gains potential energy, the mass must lose kinetic energy to keep the total energy constant. As the extension of the spring decreases, the spring loses potential energy which leads to a gain in kinetic energy (speed).

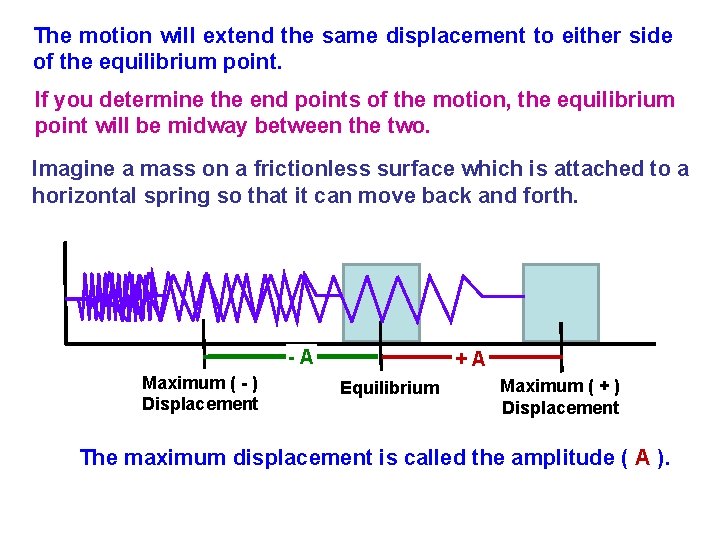
The motion will extend the same displacement to either side of the equilibrium point. If you determine the end points of the motion, the equilibrium point will be midway between the two. Imagine a mass on a frictionless surface which is attached to a horizontal spring so that it can move back and forth. -A Maximum ( - ) Displacement +A Equilibrium Maximum ( + ) Displacement The maximum displacement is called the amplitude ( A ).

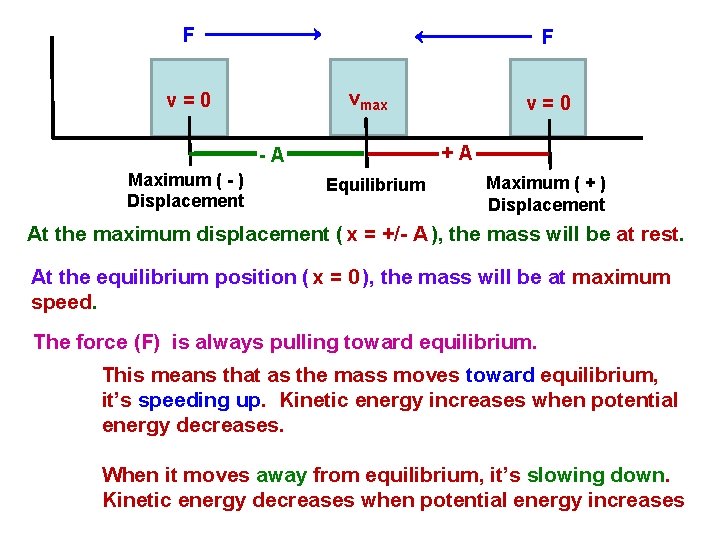
F F vmax v=0 +A -A Maximum ( - ) Displacement v=0 Equilibrium Maximum ( + ) Displacement At the maximum displacement ( x = +/- A ), the mass will be at rest. At the equilibrium position ( x = 0 ), the mass will be at maximum speed. The force (F) is always pulling toward equilibrium. This means that as the mass moves toward equilibrium, it’s speeding up. Kinetic energy increases when potential energy decreases. When it moves away from equilibrium, it’s slowing down. Kinetic energy decreases when potential energy increases

The total energy of the oscillator can then be determined by using one of the end points where the kinetic energy is zero: ETot = ½ k A 2 (Since kinetic energy is zero, the total energy is simply the elastic energy) Using the conservation of energy equation: Etot = ½ m v 2 + ½ k x 2 ½ k A 2 = ½ mv 2 + ½ k x 2 Use the above relationship to determine an expression for the speed ( v ) of the mass as a function of displacement ( x ). k A 2 - k x 2 = k ( A 2 - x 2 ) = mv 2 ( k / m ) ( A 2 - x 2 ) = (k / m) ( A 2 - x 2 ) = v v 2 (k / m) is extremely important to simple harmonic motion.

v = (k / m) ( A 2 - x 2 ) This equation shows us why the maximum speed is at equilibrium ( x = 0 ) and the minimum speed is zero at the maximum displacement ( x = A ). The number of complete motions (oscillations) it makes per unit time is called the frequency ( f ). We use the standard unit of seconds for time. 1 oscillation per second is given the unit of 1 Hertz ( Hz ). f = 1/(2 p) (k / m) The time it takes the mass to move one full motion ( from one side to the other side AND BACK ) is called the period ( T ). The period will be in units of seconds. T = 1 / f T =(2 p) (m / k) T = period This is on your equation sheet.

The period of a simple harmonic oscillator DOES NOT depend on the amplitude! In the case of a spring oscillator, the period depends on the mass and the spring constant. Earlier, we said that (k / m) is extremely important to simple harmonic motion. (k / m) = 2 pf f = frequency (k / m) = w w = angular frequency Summary of equations: v = (k / m) ( A 2 - x 2 ) f = 1/(2 p) T =(2 p) (k / m) (m / k)

A horizontal spring oscillator has 0. 400 kg mass that slides over a frictionless surface. The spring constant is 35. 0 N/m, and the maximum displacement is 0. 200 m. Determine the frequency of the oscillator. Determine the period of the oscillator. Determine the maximum velocity of the oscillator.

Determine the maximum acceleration of the oscillator. Another oscillator has an amplitude of 0. 350 m and a frequency of 2. 00 Hz. Determine the maximum acceleration of this oscillator.

If a mass is hanging from a vertical spring, it will also undergo simple harmonic motion. Although, there is gravitational potential energy as well as elastic potential energy and kinetic energy, the equations of motion are the same! There will be a shift in the equilibrium position ( xo ) : k xo = mg [ equilibrium; forces cancel ] This shift compensates for the effects of gravity. As long as the displacement is measured from the new equilibrium position, there will be no change in the equations. v = (k / m) ( A 2 - x 2 ) f = 1/(2 p) T =(2 p) (k / m) (m / k)

A 0. 375 kg mass is placed on a vertical spring. The spring stretches 0. 210 m to where the mass will hang at rest. The mass is then displaced an additional 0. 100 m ( 0. 310 m total ) and released. What is the amplitude of the oscillator? What is the spring constant? Determine the period of the oscillator.

m = 0. 375 kg xo = 0. 210 m A = 0. 100 m k = 17. 5 N/m Determine the maximum acceleration of the oscillator. Determine the maximum velocity of the oscillator. Determine the speed of the mass when it is midway between equilibrium and its amplitude ( a displacement of 0. 050 m ).

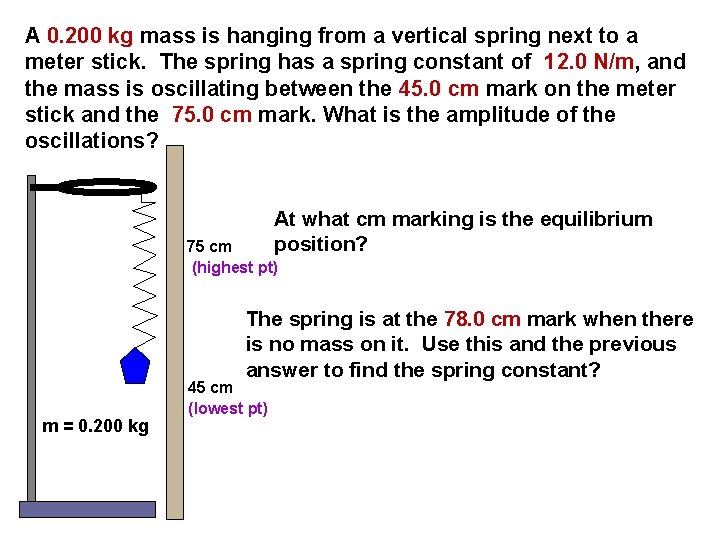
A 0. 200 kg mass is hanging from a vertical spring next to a meter stick. The spring has a spring constant of 12. 0 N/m, and the mass is oscillating between the 45. 0 cm mark on the meter stick and the 75. 0 cm mark. What is the amplitude of the oscillations? At what cm marking is the equilibrium position? 75 cm (highest pt) The spring is at the 78. 0 cm mark when there is no mass on it. Use this and the previous answer to find the spring constant? m = 0. 200 kg 45 cm (lowest pt)

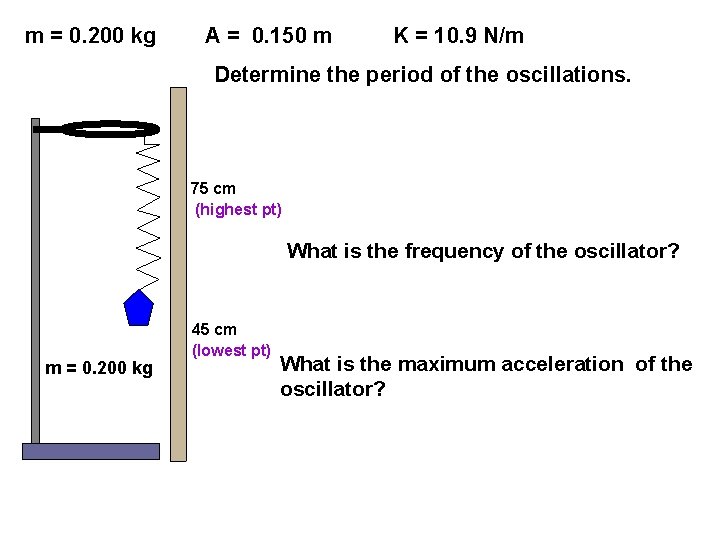
m = 0. 200 kg A = 0. 150 m K = 10. 9 N/m Determine the period of the oscillations. 75 cm (highest pt) What is the frequency of the oscillator? m = 0. 200 kg 45 cm (lowest pt) What is the maximum acceleration of the oscillator?

PENDULUM MOTION Pendulum motion is a type of harmonic motion. It is not truly simple harmonic motion, but it approximates SHM very well for small angles. The restoring force for the pendulum is mg sin q. q L BUT this force does not change linearly with displacement, so it’s not truly SIMPLE harmonic motion. T For small angles, however, sin q = q. (in radians) This gives us: F = - mg q q=x/L q mg n g si q SO: k = mg / L m SO: F = - [ mg / L ] x 2 pf= k/m 2 pf = g/L

Like a mass on a spring, the motion of the mass will extend the same displacement to either side of the equilibrium point. This maximum displacement is called the amplitude ( A ). A A The Equilibrium Point At the maximum displacement ( A ), the mass will be at rest as its motion in one direction will stop before it moves in the other direction. This is also the point where the mass will have the greatest force and acceleration. At the equilibrium point, the mass will be moving the fastest. The net force and acceleration will be zero.

The period and frequency are NOT affected by the amplitude! The pendulum will have the same period when it’s moving just a little as when it is moving a lot. The period of a simple pendulum depends on the length of the string and the acceleration of gravity. For a simple pendulum the frequency can be described by the following equation: 1 f = g/L 2 p The period would then be: T = 2 p L/g f = frequency T = period g = gravity L = the length of the pendulum

Determine the period of a pendulum that is 1. 0 m long. Determine the frequency of this pendulum. How would the frequency be changed if this set-up were brought to the moon where the gravity is 1/6 that of Earth?

A bowling ball is hung from the ceiling of a large room. When the ball is set into harmonic motion by releasing it at an angle, it moves forward and back to its starting point in 3. 6 s. How long is the string from which the ball is hanging?