OS 3 Wave PropertiesModels 1 ModelSomething used to

OS 3 Wave Properties/Models 1

Model-Something used to represent something else ¡ Can be bigger, smaller or same size Models have limitation-never have the exact same properties as the real object

Models of Light Wave model Particle model 3

Wave model-thought of as a traditional wave that can transfer energy Pros: Waves reflect, refract, have wavelengths and frequencies Cons: Wave needs a medium and can NOT travel through a vacuum-light can

Particle Model-Light thought of as particles Pros: particles reflect, affected by gravity, change speed in a new medium, have color, do not need a medium Cons: particles do not refract (bend) according to Snell’s Law

Scientists invented their own model for light called a photon Photon-Particle-like bundle of energy that moves like a wave ¡ Contains both particle and wave properties

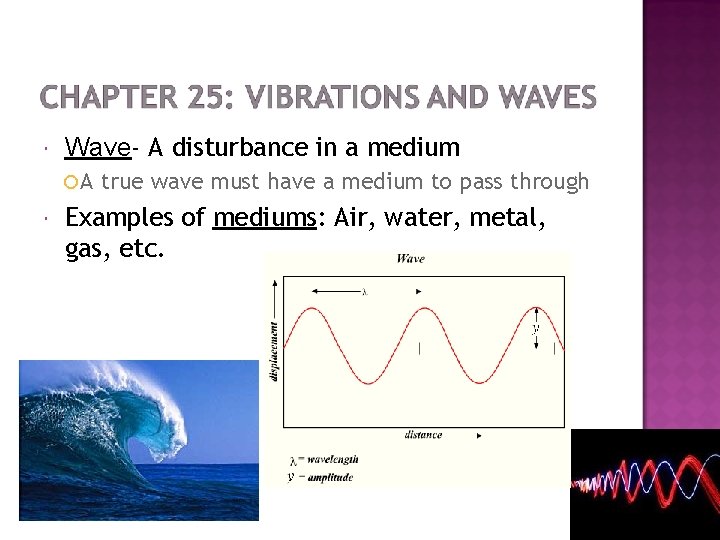
Wave- A disturbance in a medium ¡A true wave must have a medium to pass through Examples of mediums: Air, water, metal, gas, etc.

Waves transfer energy from one place to another with little transfer of the medium itself

1. Transverse Waves 2. Longitudinal Waves

Transverse Waves-The direction of propagation (motion) of the wave is perpendicular to the disturbance ¡ Examples: Water waves, light waves, radio waves, stretched strings of musical instruments

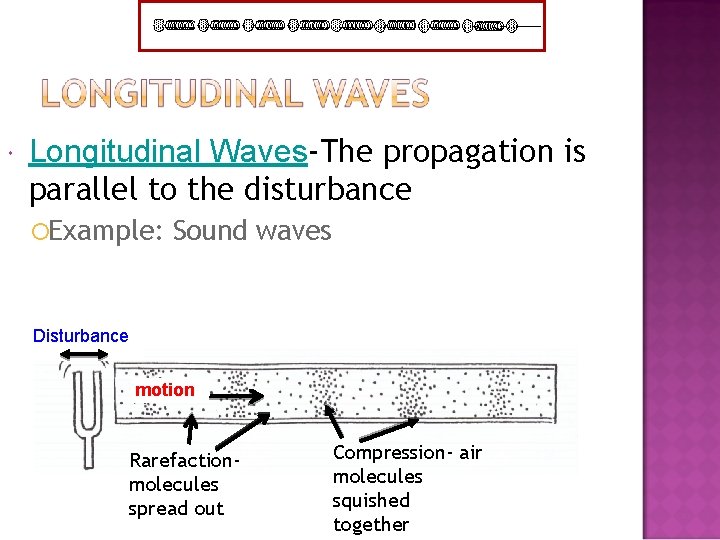
Longitudinal Waves-The propagation is parallel to the disturbance ¡Example: Sound waves Disturbance motion Rarefactionmolecules spread out Compression- air molecules squished together

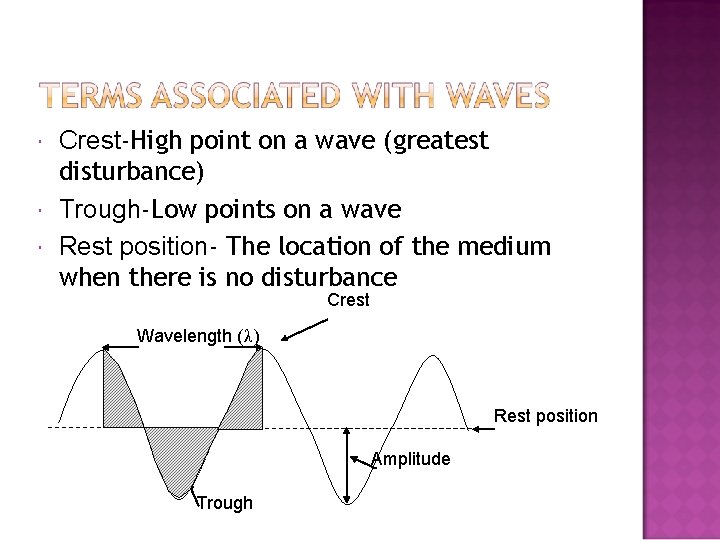
Crest-High point on a wave (greatest disturbance) Trough-Low points on a wave Rest position- The location of the medium when there is no disturbance Crest Wavelength (λ ) Rest position Amplitude Trough

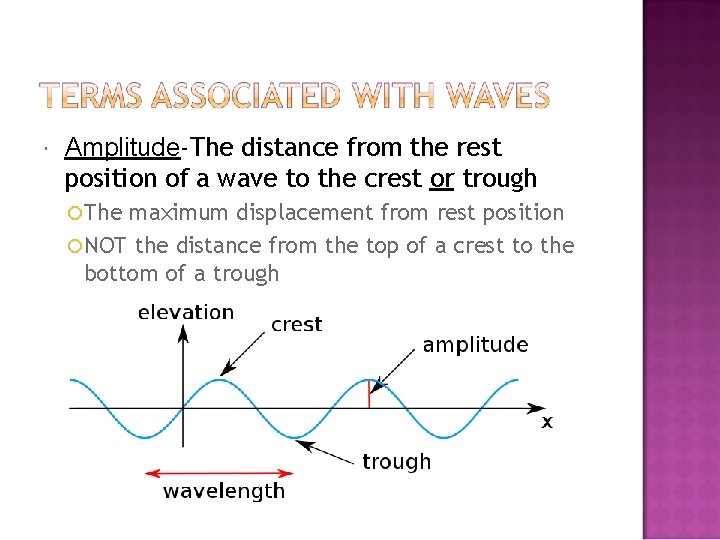
Amplitude-The distance from the rest position of a wave to the crest or trough ¡ The maximum displacement from rest position ¡ NOT the distance from the top of a crest to the bottom of a trough

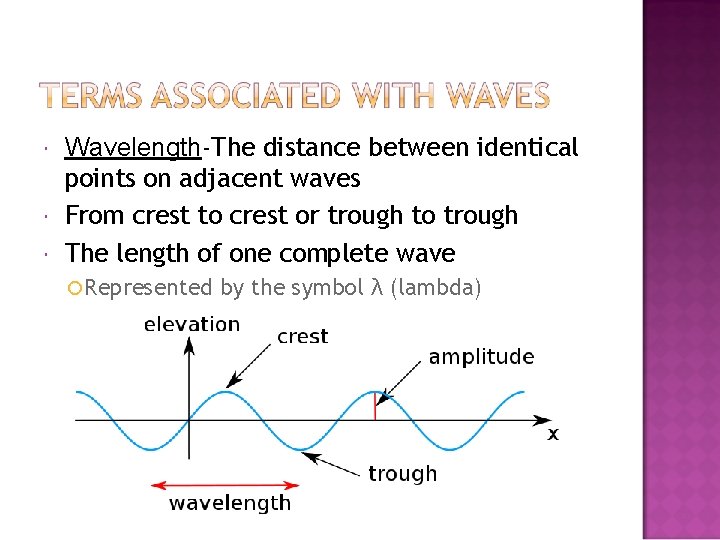
Wavelength-The distance between identical points on adjacent waves From crest to crest or trough to trough The length of one complete wave ¡ Represented by the symbol λ (lambda)

Spot Check What letter represents the wavelength? What letter represents the amplitude? Wavelength = A Amplitude = D 15

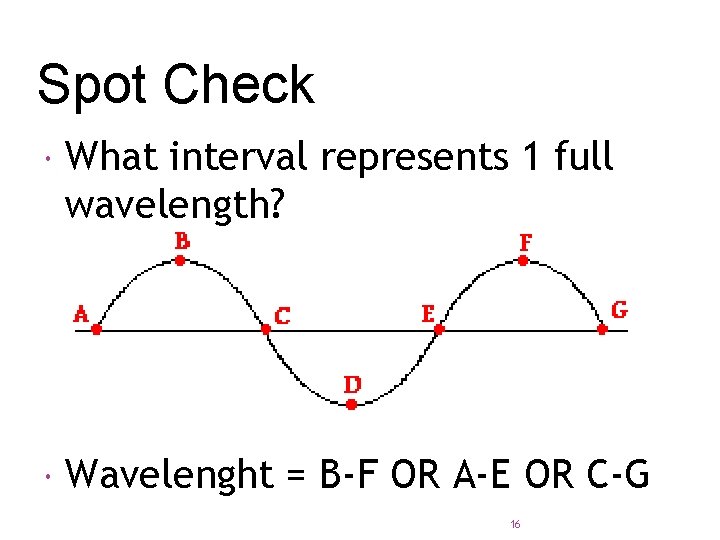
Spot Check What interval represents 1 full wavelength? Wavelenght = B-F OR A-E OR C-G 16

Frequency- The number of waves passing a point each second or how often waves are passing ¡ NOT how fast the waves are moving Symbol: f Measured in waves/sec, cycles/sec, 1/sec or hertz (Hz)

Period- The amount of time it takes for one wave to pass a point Period is symbolized by T Measured in seconds

Frequency and period are inversely related (reciprocals) f=1/T or T=1/f

Example: A pendulum makes 2 back and forth swings in 1 sec. ¡Frequency = 2 Hz ¡Period=1/2 second (time needed to complete 1 vibration) 20

Example: Tim Ahlstrom of Oconomowoc, WI holds the record for hand clapping: 793 times in 60 seconds Calculate the frequency Calculate the period Frequency = 793/60 = 13 hz Period = 1/13 =. 077 s 21

Bumblebees flap their wings at ~130 flaps/sec. ¡ Produce a sound of 130 Hz Honeybees flap their wings at 225 flaps/sec. ¡ Produces a higher pitched sound of 225 Hz Mosquito flaps its wings at 600 flaps/sec. ¡ Produces a high-pitched sounds of 600 Hz

The speed of a wave depends on the medium (material) the wave moves through For example: In air, all sound waves whether they have high frequency or low frequency all travel at the same speed

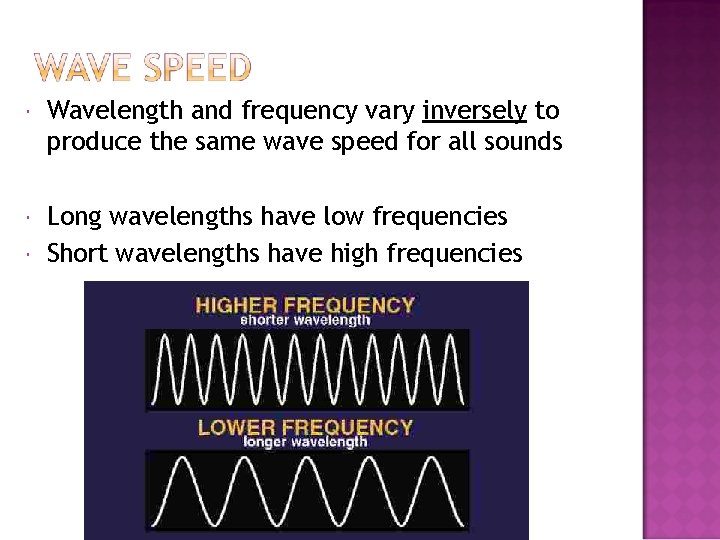
Wavelength and frequency vary inversely to produce the same wave speed for all sounds Long wavelengths have low frequencies Short wavelengths have high frequencies

In general, the more rigid the material (molecules closer together), the faster the wave moves ¡ Example: Sound waves travel fastest in solids and slowest in gases

Light or Sound? Which travels faster light or sound? Light: 3 X 108 m/s Sound: 343 m/s ¡Phet Simulations 26

Reflection and Transmission http: //www. kettering. edu/physics/drussell/ Demos/reflect. html 27

To Recap…. Does changing frequency affect the speed of a wave? NO! Does changing wavelength affect the speed of a wave? NO! Does amplitude affect the speed of a wave? NO! 28

The formula for the speed of a wave is: ¡ Wave speed = wavelength X frequency V=λf V=wave speed (m/s or cm/s) λ=wavelength (m or cm) f=frequency (waves/s, cycles/s, 1/s, or Hz)

If a sound wave has a frequency of 396 Hz and a wavelength of 0. 86 meters, what is the wave speed? 1. List the variables Hz ¡ λ=0. 86 m ¡ V=? ¡ f=396 2. Set up the equation ¡ V=λf ¡ V=(0. 86 m)(396 Hz) ¡ V=340 m/s

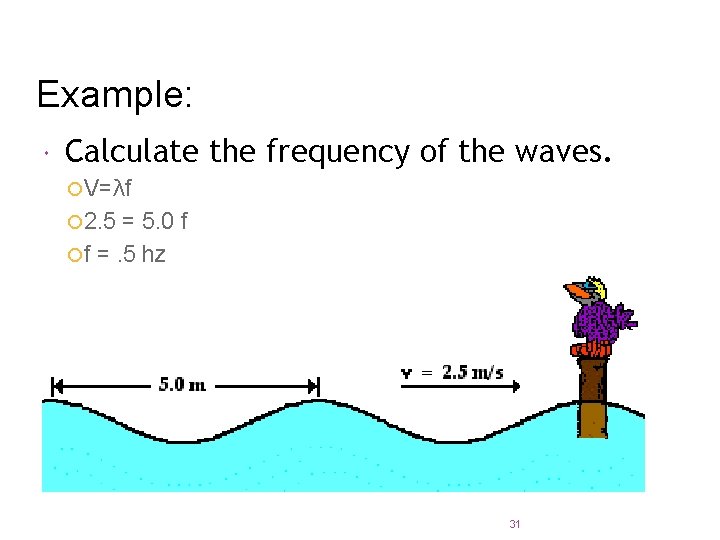
Example: Calculate the frequency of the waves. ¡ V=λf ¡ 2. 5 = 5. 0 f ¡ f =. 5 hz 31

Example: If the frequency of a wave triples, what happens to the wavelength? λ = 1/3 If the frequency of the wave triples, what happens to the velocity? v =same (only dependent on meduim) V=λf 32

The energy of a wave depends primarily on its frequency The only energy problems we do will be related to the energy of light E=hf Formula: E=energy (Joules, J) f=frequency (waves/s or Hz) h=Planck’s constant (6. 6 x 10 -34 J s)

Standing wave-A wave in which parts of the wave remain stationary and the wave appears to be not traveling Results from the interference between an incident (original) wave and a reflected one

Node-Any part of a standing wave that remains stationary Antinode-The positions on a standing wave where the largest amplitudes occur ¡ Example: Different standing waves can be produced by shaking the rope at different frequencies ¡ Phet Simulations

Superposition-The adding of waves

Interference-When 2 or more waves overlap

Constructive interference (reinforcement)-Wave crests overlap to produce an increase in wave amplitude Destructive interference (cancellation)-When a crest and trough overlap, resulting in a wave of decreased amplitude

Interference produces beats Beat-Result of alternate cancellation and reinforcement of 2 sound waves with slightly different frequencies

The vibration of an object that is made to vibrate by another vibrating object that is nearby ¡ One object vibrates to make another object vibrate Example: The sounding board in a musical instrument

The frequency that requires the least amount of energy to continue the vibration

Resonance-Resound or sound again When the frequency of forced vibrations on an object match the object’s natural frequency Results in a dramatic increase in amplitude

Example: Swinging When pumping you pump with the natural frequency of the swing Even small pumps or pushes from someone else will produce large amplitudes if delivered in rhythm with the natural frequency of the swinging motion

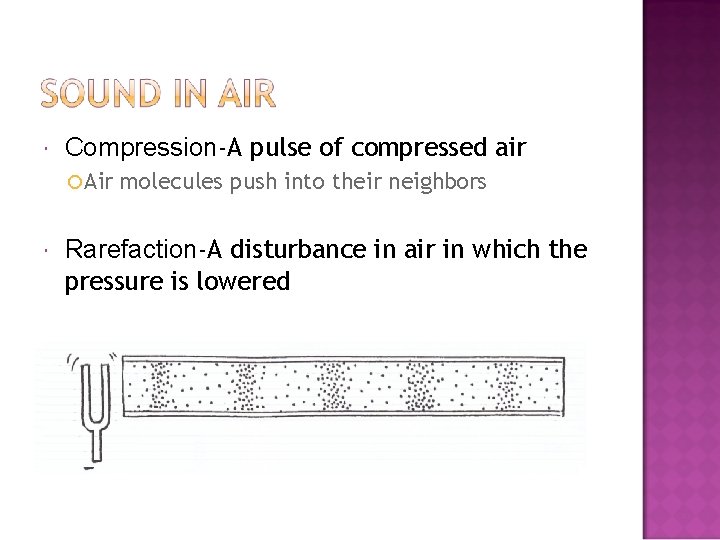
Compression-A pulse of compressed air ¡ Air molecules push into their neighbors Rarefaction-A disturbance in air in which the pressure is lowered

Loudness is a physiological sensation sensed in the brain Subjective but related to sound intensity Roughly, loudness follows the intensity decibel scale

Longitudinal Waves transfer energy as the disturbance is in the same direction as the wave (a. LONG the wave) 46