Orthogonal Transforms Fourier Walsh Hadamard Review Introduce the











































































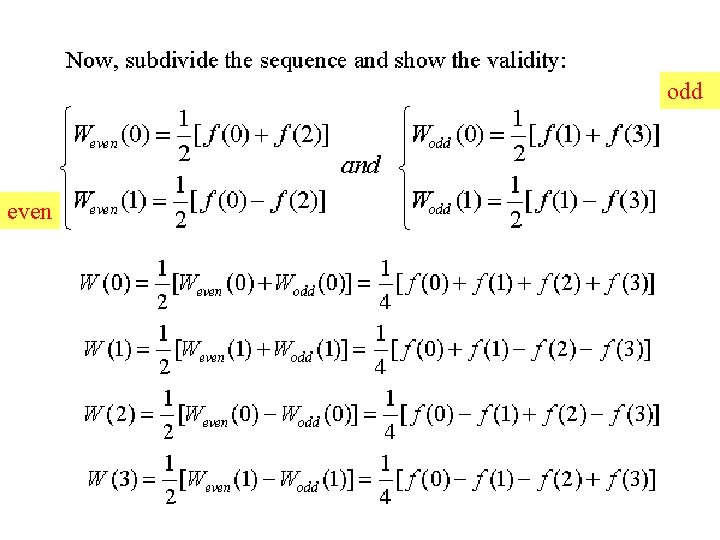





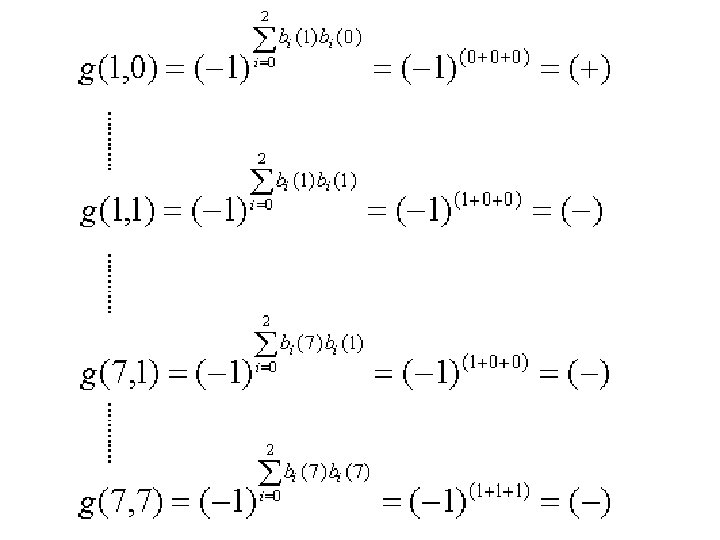




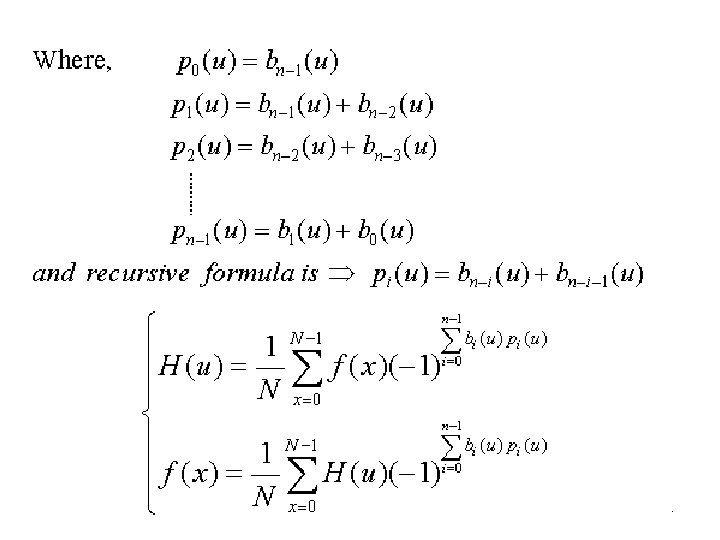

















- Slides: 121

Orthogonal Transforms Fourier Walsh Hadamard

Review • Introduce the concepts of base functions: – For Reed-Muller, FPRM – For Walsh • • • Linearly independent matrix Non-Singular matrix Examples Butterflies, Kronecker Products, Matrices Using matrices to calculate the vector of spectral coefficients from the data vector

Orthogonal Functions


Illustrate it for Walsh and RM




Mean Square Error



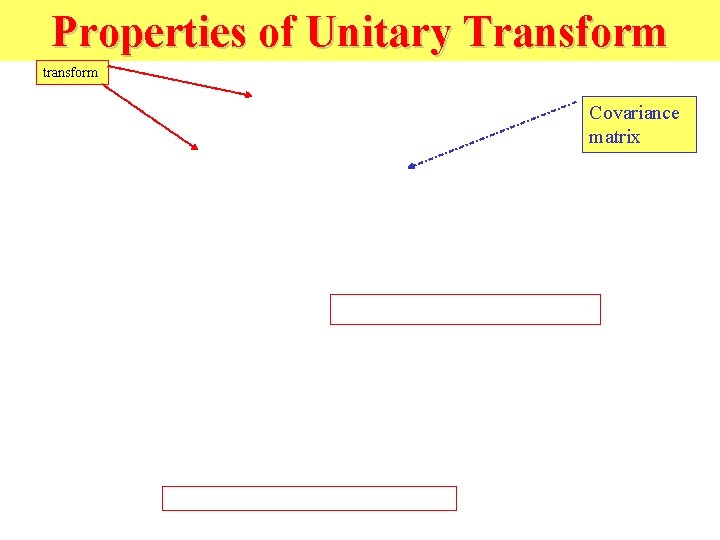
Important result

• We want to minimize this kinds of errors. • Other error measures are also used.

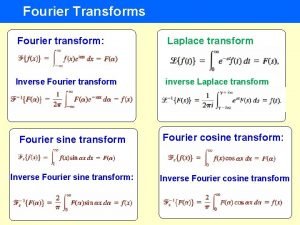
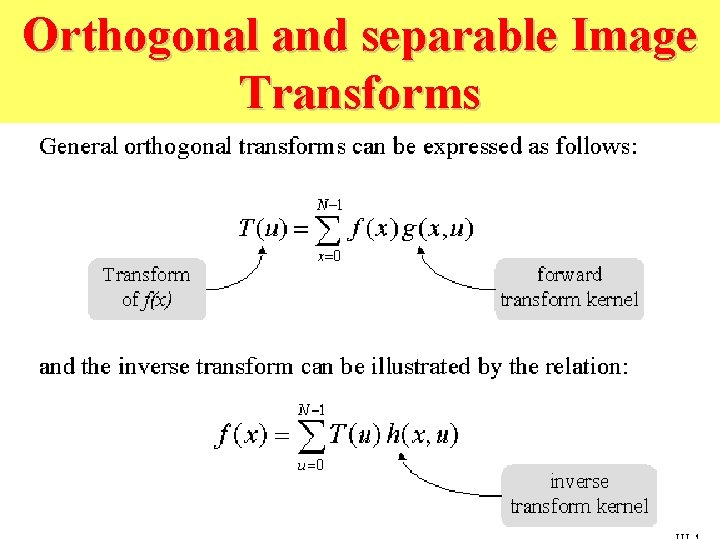
Unitary Transforms • Unitary Transformation for 1 -Dim. Sequence – Series representation of – Basis vectors : – Energy conservation : Here is the proof

• Unitary Transformation for 2 -Dim. Sequence – Definition : – Basis images : – Orthonormality and completeness properties • Orthonormality : • Completeness :

• Unitary Transformation for 2 -Dim. Sequence – Separable Unitary Transforms • separable transform reduces the number of multiplications and additions from to – Energy conservation

Properties of Unitary Transform transform Covariance matrix

Example of arbitrary basis functions being rectangular waves

This determining first function determines next functions

0 1
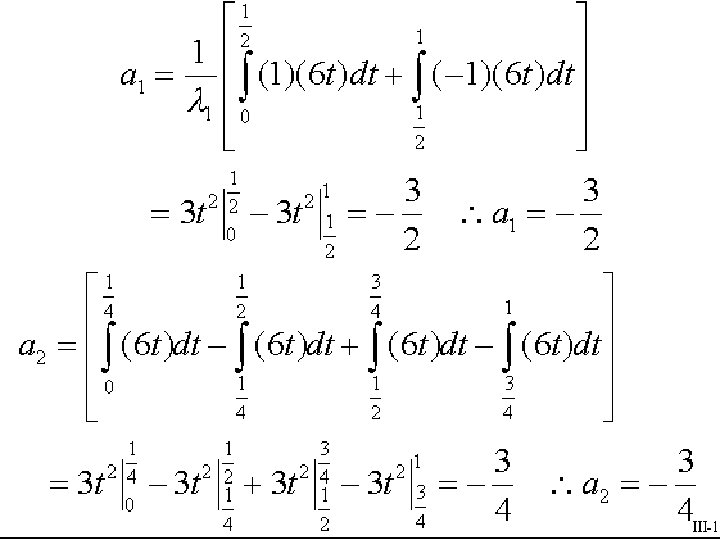

Small error with just 3 coefficients

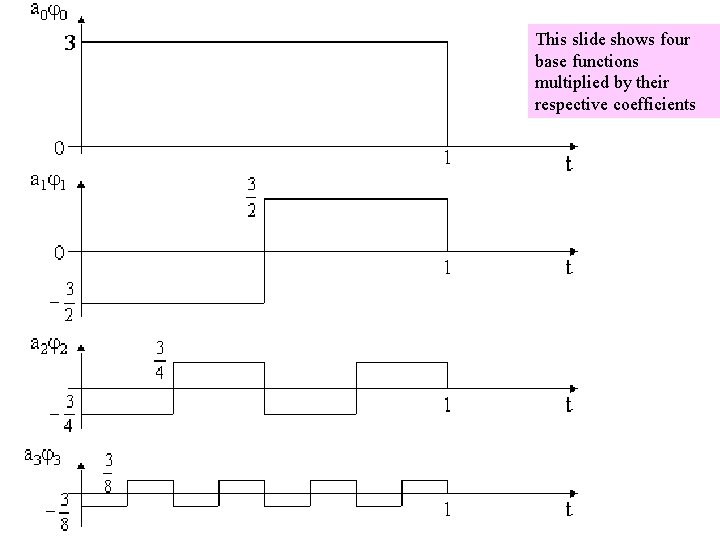
This slide shows four base functions multiplied by their respective coefficients

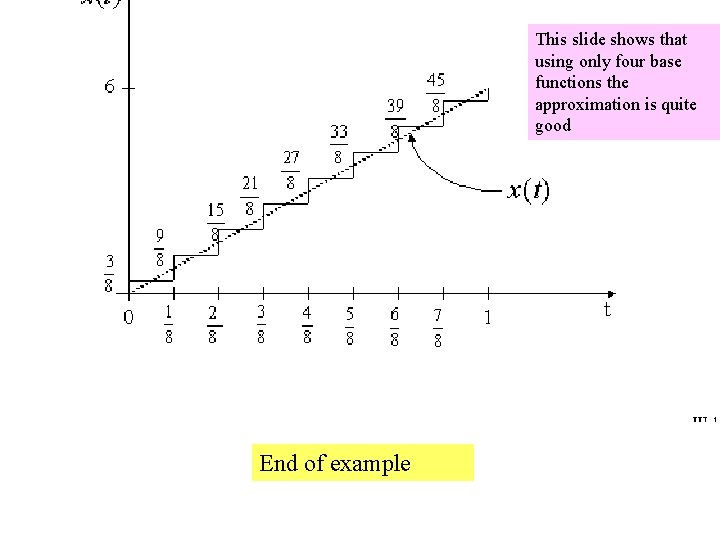
This slide shows that using only four base functions the approximation is quite good End of example

Orthogonal and separable Image Transforms

Extending general transforms to 2 dimensions

Forward transform inverse transform separable

Fourier Transform separable

Extension of Fourier Transform to two dimensions




Discrete Fourier Transform (DFT) New notation


Fast Algorithms for Fourier Transform Task for students: 2 Draw the butterfly for these matrices, similarly as we have done it for Walsh and Reed-Muller Transforms Pay attention to regularity of kernels and order of columns corresponding to factorized matrices

Fast Factorization Algorithms are general and there is many of them

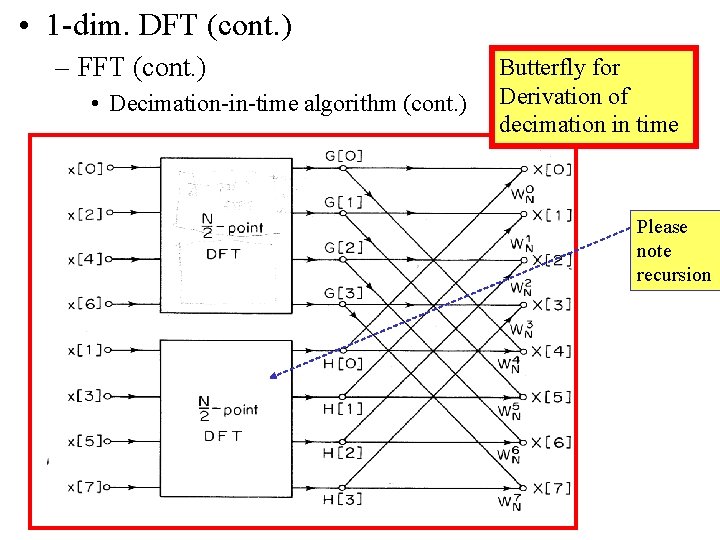
• 1 -dim. DFT (cont. ) – Calculation of DFT : Fast Fourier Transform Algorithm (FFT) • Decimation-in-time algorithm Derivation of decimation in time

• 1 -dim. DFT (cont. ) – FFT (cont. ) • Decimation-in-time algorithm (cont. ) Butterfly for Derivation of decimation in time Please note recursion

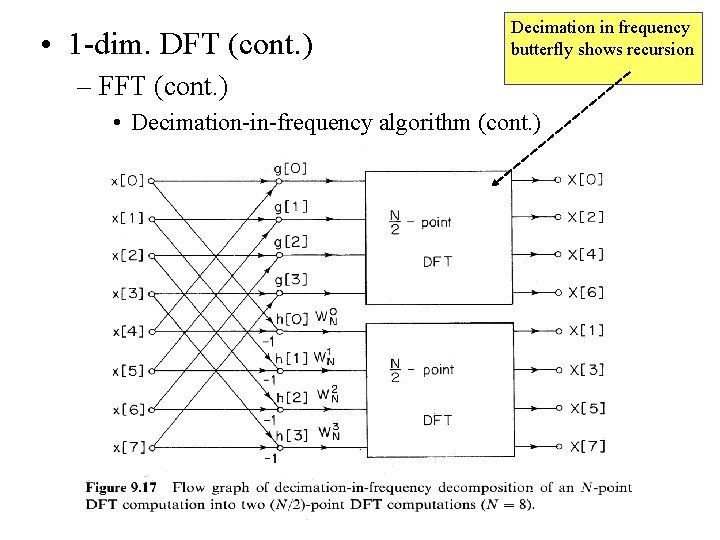
• 1 -dim. DFT (cont. ) – FFT (cont. ) • Decimation-in-frequency algorithm (cont. ) Derivation of Decimation-infrequency algorithm

• 1 -dim. DFT (cont. ) Decimation in frequency butterfly shows recursion – FFT (cont. ) • Decimation-in-frequency algorithm (cont. )

Conjugate Symmetry of DFT – For a real sequence, sequence the DFT is conjugate symmetry

Use of Fourier Transforms for fast convolution

Calculations for circular matrix

By multiplying

In matrix form next slide W * = Cw*


Here is the formula for linear convolution, we already discussed for 1 D and 2 D data, images

Linear convolution can be presented in matrix form as follows:

As we see, circular convolution can be also represented in matrix form

Important result

Inverse DFT of convolution

• Thus we derived a fast algorithm for linear convolution which we illustrated earlier and discussed its importance. • This result is very fundamental since it allows to use DFT with inverse DFT to do all kinds of image processing based on convolution, such as edge detection, thinning, filtering, etc.

2 -D DFT

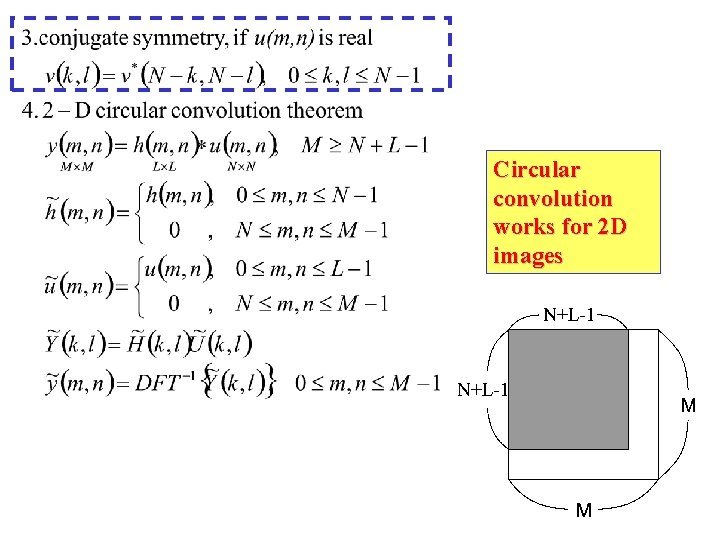
Circular convolution works for 2 D images

Circular convolution works for 2 D images So we can do all kinds of edge-detection, filtering etc very efficiently • 2 -Dim. DFT (cont. ) – example (a) Original Image (b) Magnitude (c) Phase

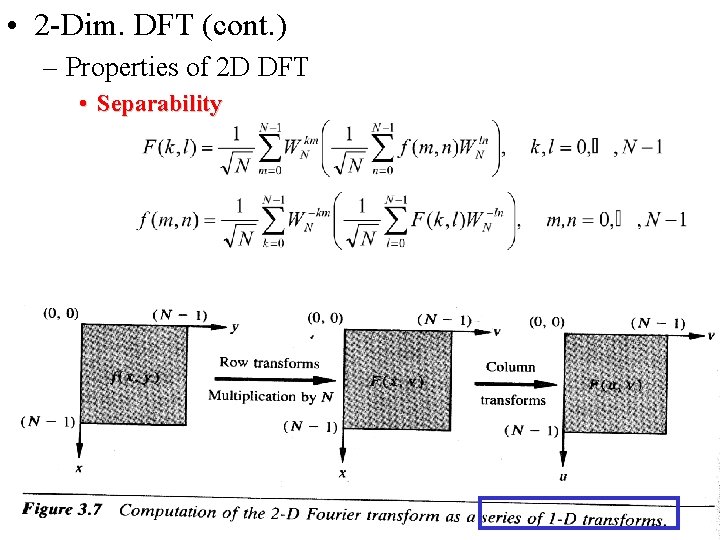
• 2 -Dim. DFT (cont. ) – Properties of 2 D DFT • Separability

• 2 -Dim. DFT (cont. ) – Properties of 2 D DFT (cont. ) • Rotation (a) a sample image (b) its spectrum (c) rotated image (d) resulting spectrum

• 2 -Dim. DFT (cont. ) – Properties of 2 D DFT • Circular convolution and DFT • Correlation

• 2 -Dim. DFT (cont. ) – Calculation of 2 -dim. DFT • Direct calculation – Complex multiplications & additions : • Using separability – Complex multiplications & additions : • Using 1 -dim FFT – Complex multiplications & additions : ? ? ? Three ways of calculating 2 -D DFT

Karhunen-Leove Transform(KLT) Covariance matrix


• What happens if 1?

This happens if 1

Category of transforms These are what I called earlier transforms with standard butterflies

Discrete Cosine Transform (DCT) This is DCT

DCT is an orthogonal transformm so its inverse kernel is the same as forward kernel This is inverse DCT


DCT can be obtained from DFT

Discrete Cosine Transform is asymptotically equivalent to Karhunen-Loeve We take a 2 N-point DFT: This is why guys in industry believe that only DCT is worth their work.

Properties of DCT: real, orthogonal, energycompacting, eigenvector-based

The eigenvectors of R and Qc are very close

– Basis Functions for 1 -dim. DCT(N = 16)

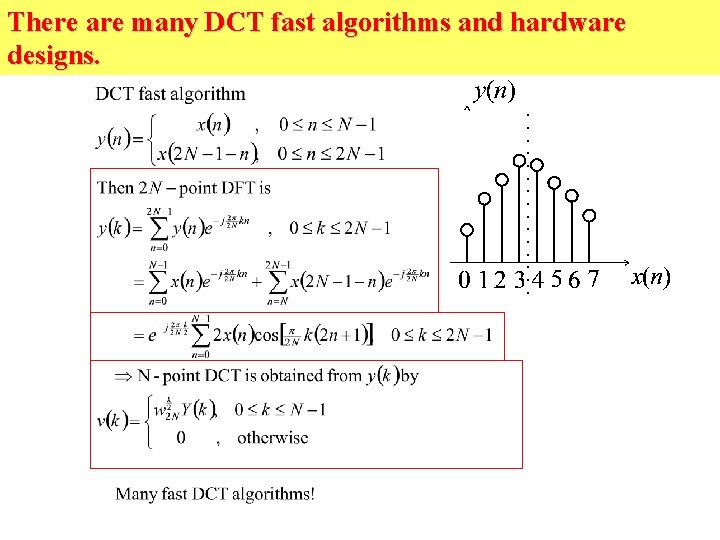
There are many DCT fast algorithms and hardware designs.

There are many DCT fast algorithms and hardware designs. Many fast algorithms are available fast algorithm : Lee(1 -D), Lee-Cho(2 -D) VLSI algorithm : regularity, local interconnection, moduality ref: 1. Nam Ik Cho and Sang Uk Lee, “Fast algorithm and implementation of 2 -D DCT. ” IEEE Trans Circuits and Systems, vol. 38, no. 3, pp. 297 -305, March 1991. 2. Nam Ik Cho and Sang Uk Lee, “DCT algorithm for VLSI parallel implementation” IEEE Trans. ASSP, vol. ASSP-38, no. 1, pp. 121 -127, Jan, 1990.

Discrete Sine Transform(DST) Similar to DCT.

• 1 -dim. DST (cont. ) – Basis Functions for 1 -dim. DST (N=16)

Walsh Transform

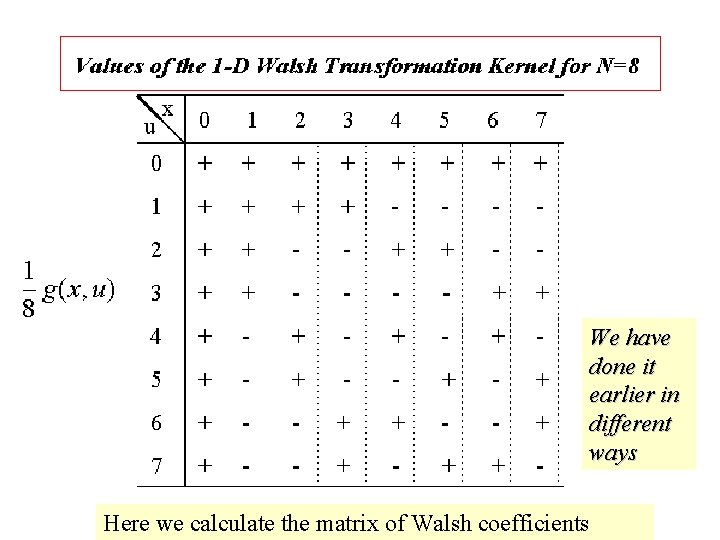
Here we calculate the matrix of Walsh coefficients

Here we calculate the matrix of Walsh coefficients

Here we calculate the matrix of Walsh coefficients

We have done it earlier in different ways Here we calculate the matrix of Walsh coefficients

Symmetry of Walsh Think about other transforms that you know, are they symmetric?

Two-Dimensional Walsh Transform

Two-dimensional Walsh Inverse Two-dimensional Walsh

Properties of Walsh Transforms

Here is the separable 2 -Dim Inverse Walsh

Example for N=4
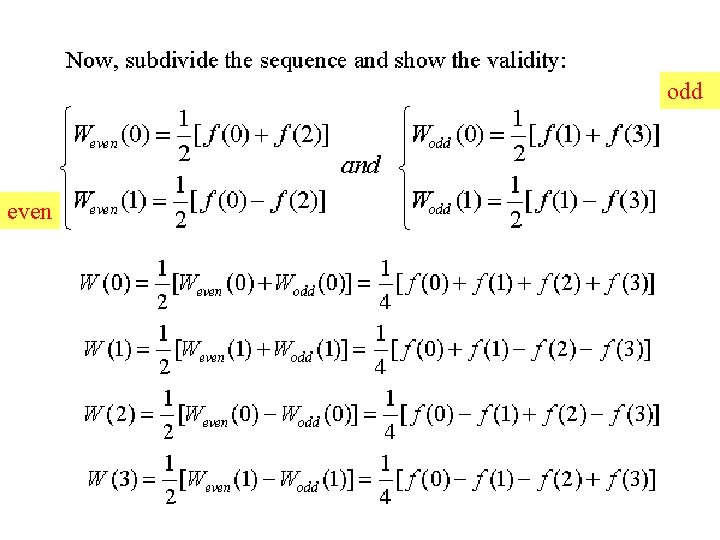
odd even

Discuss the importance of this figure

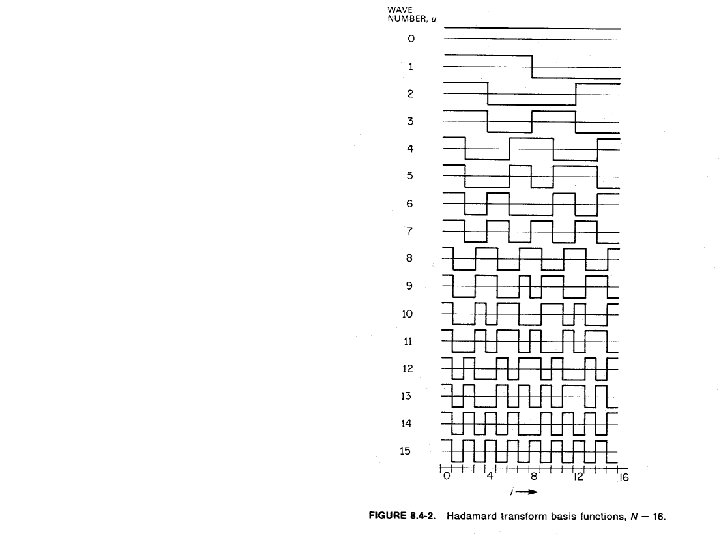
Hadamard Transform We will go quickly through this material since it is very similar to Walsh


separable

Example of calculating Hadamard coefficients – analogous to what was before
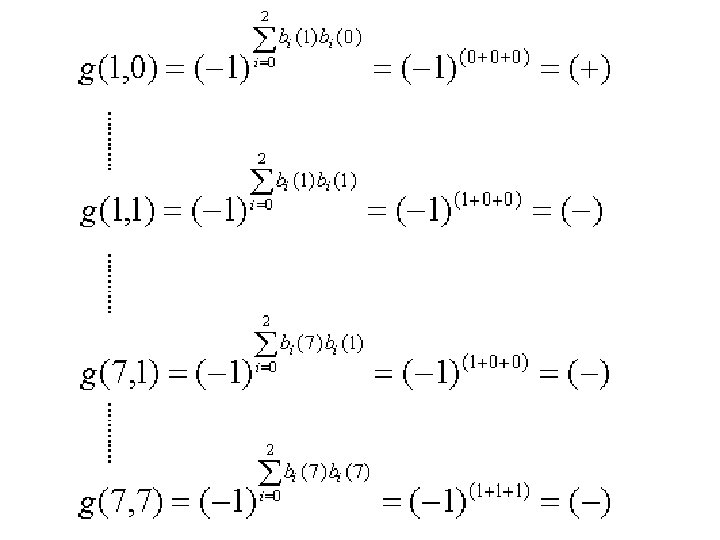




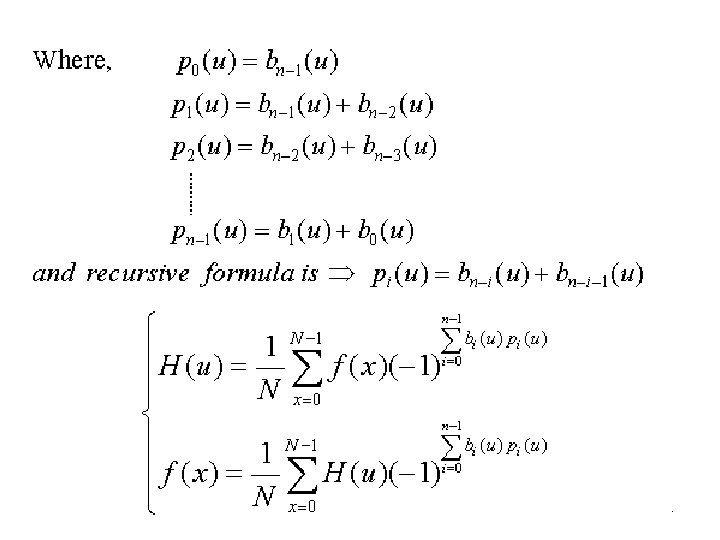


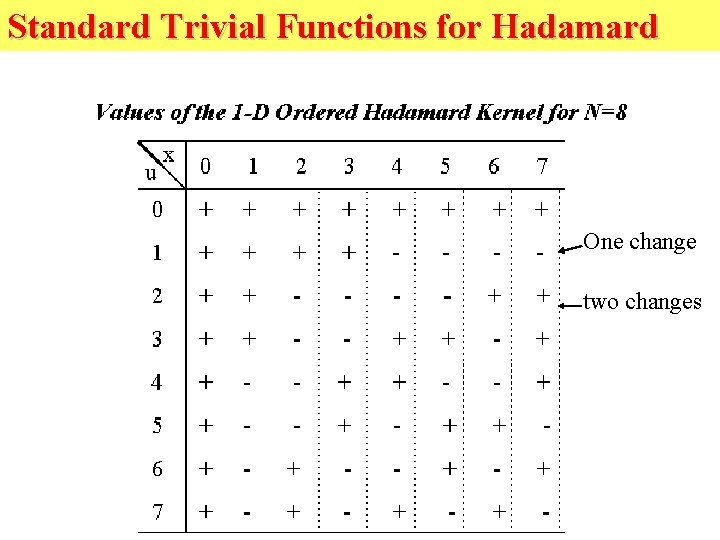
Standard Trivial Functions for Hadamard One change two changes


Discrete Walsh-Hadamard transform Now we meet our old friend in a new light again!





Relationship between Walsh-ordered and Hadamard-ordered

Haar Transform • Haar transform – Haar function (1910, Haar) : periodic, orthonormal, complete Nonsinusoidal orthogonal function



Slant transform




SVD(Singular Value Decomposition)



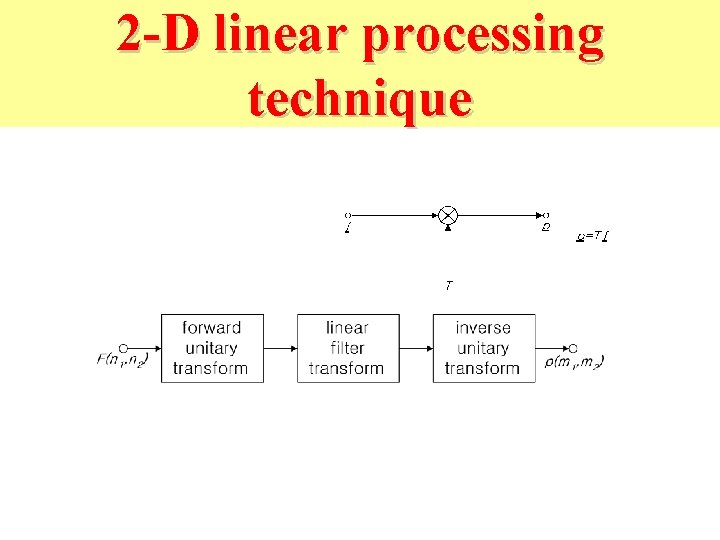
2 -D linear processing technique


Questions to Students 1. 2. You do not have to remember derivations but you have to understand the main concepts. Much software for all discussed transforms and their uses is available on internet and also in Matlab, Open. CV, and similar packages. 1. How to create an algorithm for edge detection based on FFT? 2. How to create a thinning algorithm based on DCT? 3. How to use DST for convolution – show example. 4. Low pass filter based on Hadamard. 5. Texture recognition based on Walsh
 Lie2d
Lie2d Hadamard gate
Hadamard gate Parent functions and transformations
Parent functions and transformations Dft shifting property
Dft shifting property Hadamard transform in digital image processing
Hadamard transform in digital image processing Hadamard's theorem in complex analysis
Hadamard's theorem in complex analysis Orthogonal functions in fourier series
Orthogonal functions in fourier series Sine fourier transform
Sine fourier transform Fourier series and orthogonal functions
Fourier series and orthogonal functions Social problem is seen as a deviation
Social problem is seen as a deviation B. timothy walsh
B. timothy walsh Mary g walsh writing center
Mary g walsh writing center Landis walsh
Landis walsh Bud walsh into the wild
Bud walsh into the wild Pearl sydenstricker buck
Pearl sydenstricker buck Thomas malory biography
Thomas malory biography Olga walsh
Olga walsh Psy walsh
Psy walsh Dr claire walsh
Dr claire walsh D walsh sdsu
D walsh sdsu Anchor container security
Anchor container security James walsh brown university
James walsh brown university Iquips
Iquips Contoh soal indeks walsh
Contoh soal indeks walsh William j. walsh
William j. walsh Walsh v wilkie
Walsh v wilkie Digital image processing
Digital image processing Konsep angka indeks
Konsep angka indeks Conor walsh harvard
Conor walsh harvard Robyn merkel walsh
Robyn merkel walsh Bernadine walsh
Bernadine walsh Haar transform for n=8
Haar transform for n=8 Dr lorraine walsh
Dr lorraine walsh Cuenta ratones ellen stoll walsh pdf
Cuenta ratones ellen stoll walsh pdf What does tiresias warn odysseus not to do?
What does tiresias warn odysseus not to do? Photosynthesis transforms light energy into chemical energy
Photosynthesis transforms light energy into chemical energy This transforms a bare stage into the world of the play
This transforms a bare stage into the world of the play Friction transforms mechanical energy to
Friction transforms mechanical energy to Friction transforms mechanical energy to
Friction transforms mechanical energy to Inverse laplace transform formula table
Inverse laplace transform formula table What is drama
What is drama Z transform tutorial
Z transform tutorial Which phase transforms srs document
Which phase transforms srs document The unit that transforms data into information is the:
The unit that transforms data into information is the: Z-transform examples
Z-transform examples Transforms of derivatives
Transforms of derivatives Image transforms
Image transforms Discontinuous forcing functions
Discontinuous forcing functions Transforms eroded parts of earth's surface into lakes
Transforms eroded parts of earth's surface into lakes Fourier sine series
Fourier sine series Ples phantom
Ples phantom Orthogonal decomposition
Orthogonal decomposition Orthogonal cutting diagram
Orthogonal cutting diagram Orthogonal coding
Orthogonal coding Orthogonal array
Orthogonal array What is unitary matrix
What is unitary matrix Inverse of transpose
Inverse of transpose Distinct eigenvalues
Distinct eigenvalues Orthogonal polynomials examples
Orthogonal polynomials examples What are the two orthogonal view of software
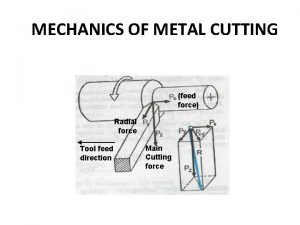
What are the two orthogonal view of software Feed force in orthogonal cutting
Feed force in orthogonal cutting Isometric drawing characteristics
Isometric drawing characteristics Blak
Blak Define orthonormal set with example
Define orthonormal set with example Orthogonal view
Orthogonal view Orthogonal cutting is dimensional metal cutting
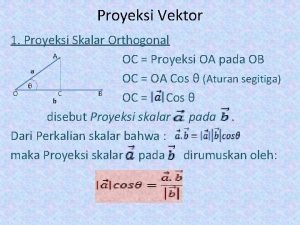
Orthogonal cutting is dimensional metal cutting Proyeksi vektor
Proyeksi vektor Theory of metal cutting
Theory of metal cutting Taguchi l18 orthogonal array
Taguchi l18 orthogonal array Irange tree
Irange tree Ofdm
Ofdm Fundamentals of computer graphics
Fundamentals of computer graphics Define orthonormal set with example
Define orthonormal set with example Orthogonality
Orthogonality Orthogonal iteration
Orthogonal iteration Orthogonal views of software in ooad
Orthogonal views of software in ooad First order linear differential equation
First order linear differential equation Orthonormal basis
Orthonormal basis Orthogonal projection
Orthogonal projection Pythogor
Pythogor What is unitary matrix
What is unitary matrix Orthogonal matrix
Orthogonal matrix Orthogonal matrix
Orthogonal matrix Cartesian equation
Cartesian equation Orthogonal transformation
Orthogonal transformation Idempotent matrix properties
Idempotent matrix properties Orthogonal
Orthogonal Orthogonal unit differentiation
Orthogonal unit differentiation Orthogonal
Orthogonal Vẽ hình chiếu đứng bằng cạnh của vật thể
Vẽ hình chiếu đứng bằng cạnh của vật thể độ dài liên kết
độ dài liên kết Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Các môn thể thao bắt đầu bằng tiếng chạy
Các môn thể thao bắt đầu bằng tiếng chạy Sự nuôi và dạy con của hươu
Sự nuôi và dạy con của hươu điện thế nghỉ
điện thế nghỉ Dot
Dot Biện pháp chống mỏi cơ
Biện pháp chống mỏi cơ Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Gấu đi như thế nào
Gấu đi như thế nào Thiếu nhi thế giới liên hoan
Thiếu nhi thế giới liên hoan Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Một số thể thơ truyền thống
Một số thể thơ truyền thống Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Ng-html
Ng-html Sơ đồ cơ thể người
Sơ đồ cơ thể người Tư thế ngồi viết
Tư thế ngồi viết Các số nguyên tố là gì
Các số nguyên tố là gì đặc điểm cơ thể của người tối cổ
đặc điểm cơ thể của người tối cổ Mật thư tọa độ 5x5
Mật thư tọa độ 5x5 Tư thế worms-breton
Tư thế worms-breton ưu thế lai là gì
ưu thế lai là gì Thẻ vin
Thẻ vin Cái miệng xinh xinh thế chỉ nói điều hay thôi
Cái miệng xinh xinh thế chỉ nói điều hay thôi Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Bổ thể
Bổ thể Từ ngữ thể hiện lòng nhân hậu
Từ ngữ thể hiện lòng nhân hậu Diễn thế sinh thái là
Diễn thế sinh thái là Tư thế ngồi viết
Tư thế ngồi viết V. c c
V. c c Làm thế nào để 102-1=99
Làm thế nào để 102-1=99 Thơ thất ngôn tứ tuyệt đường luật
Thơ thất ngôn tứ tuyệt đường luật