Origins of Signal Detection Theory Problem in Psychophysics

Origins of Signal Detection Theory ØProblem in Psychophysics v Thresholds: is sensitivity discrete or continuous? v Sensitivity confounded with response bias

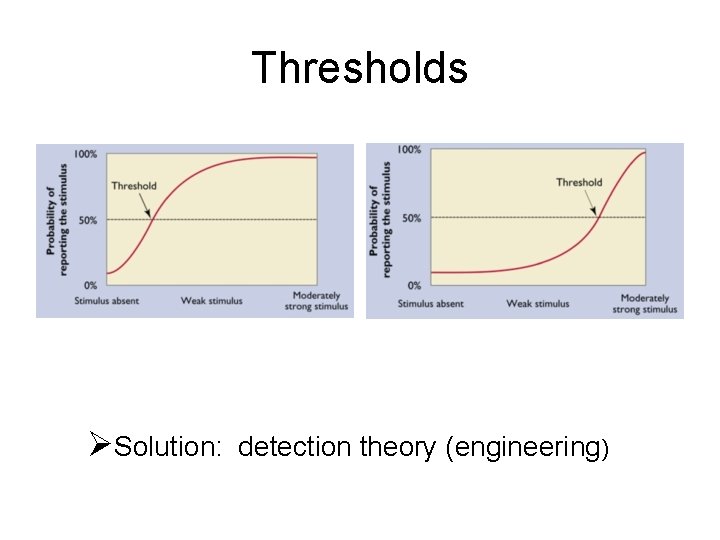
Thresholds ØSolution: detection theory (engineering)

Signal Detection Theory Response State of the World Yes Signal Hit (H) False Noise Alarm (FA) No Miss (M) Correct Rejection (CR)

Assumptions of Signal Detection Theory ØNoise is always present (i. e. in the nervous system and/or in the signal generating system) ØThe noise is normally distributed with σ2 = 1 ØFor Gaussian model ØWhen a signal is added to the noise, the distribution is shifted upward along the sensory dimension. Variance remains constant (equal variance model).

Assumptions of Signal Detection Theory ØObservers are both sensors and decision makers ØTo evaluate the occurrence of an event, observers adopt a decision criterion ØSensitivity and Response Bias are independent ØStatistical ØTheoretical ØEmpirical

Distribution of Noise and Signal + Noise

Sensitivity ’ d = z. H - z. F d’ Task Person >3. 5 very easy very sensitive 2. 6 -3. 5 moderately easy moderately sensitive 1. 6 -2. 5 moderately difficult moderately insensitive <1. 5 very difficult very insensitive

Relation of d’ to Other Statistics If μn=0 and σn=1 (i. e. , if the N distribution is unit normal) then the ROC function, in its most general form, is

Testing a Mean From One Distribution

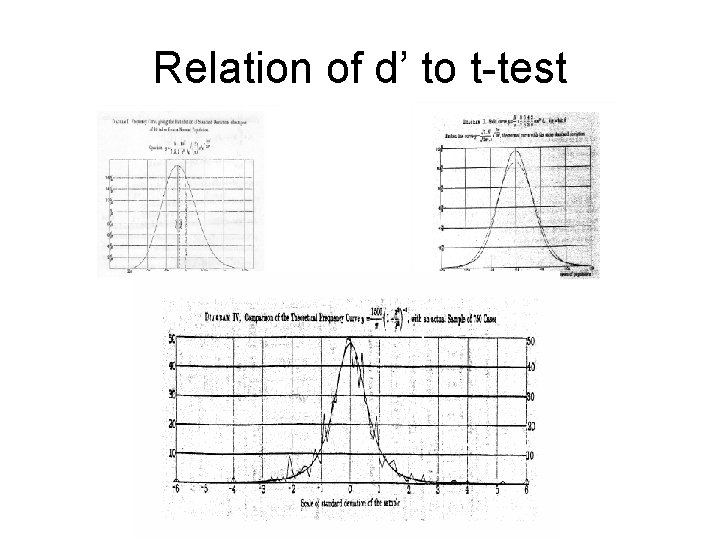
Relation of d’ to t-test

Comparing Means from Two Distributions

Standardized Mean Difference Effect Size

Response Bias = f(SN)/f(N) Lenient: 0 -1 Unbiased: 1 8 Conservative: 1 - c = -. 5(z. H + z. F) Lenient: Unbiased: <0 0 Conservative: >0

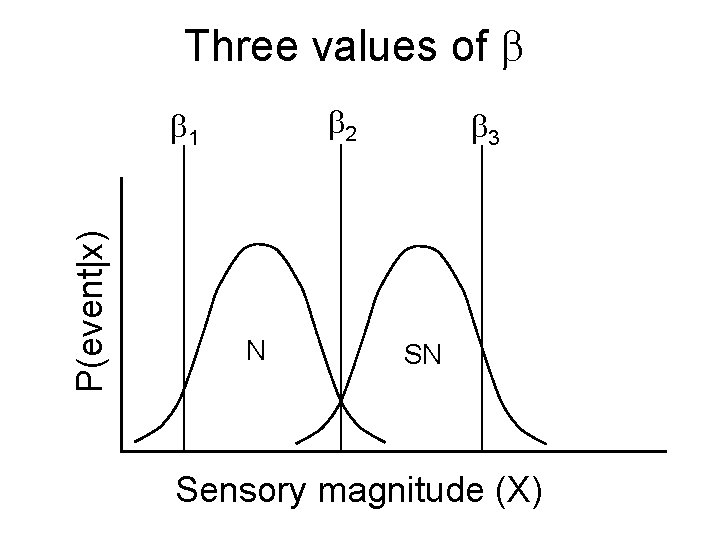
Three values of 2 P(event|x) 1 N 3 SN Sensory magnitude (X)

Receiver Operating Characteristic (ROC)

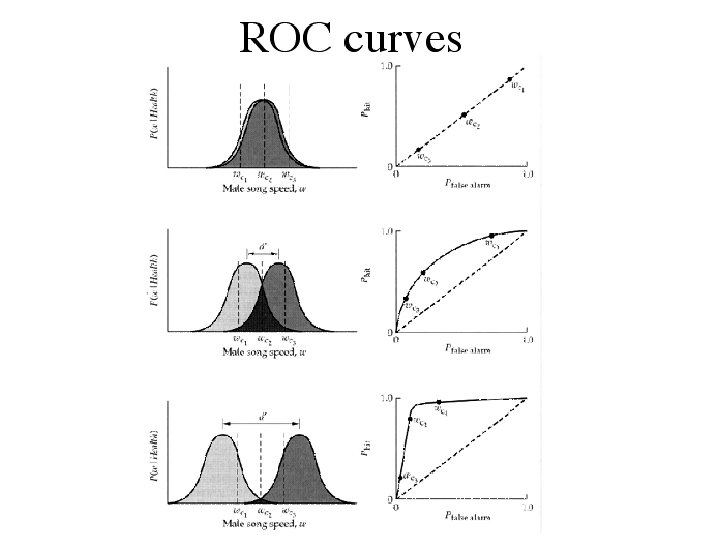
ROC Curves: Sensitivity

ROC Curves: Response Bias

ROC Curve in Z-score form 1 ZH 0 0 ZFA 1

ROC for σ2 N = σ2 SN 3 ZH 0 -3 -3 0 ZFA 3

What is Independence? • Statistical: P(A|B)=P(A) PB|A)=P(B) • Theoretical/Logical: β can vary independently of d’ • Empirical: experimental evidence is consistent with the independence assumption (e. g. Form of empirical ROC)

Three values of 2 P(event|x) 1 N 3 SN Sensory magnitude (X)

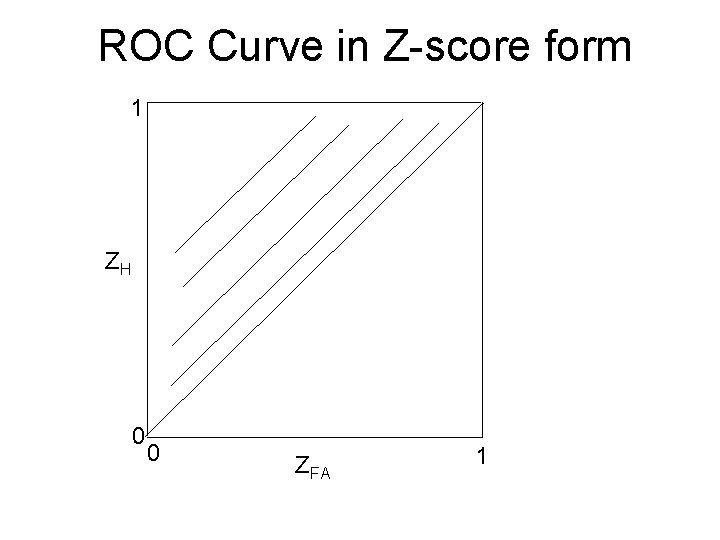
ROC Curve in Z-score form 1 ZH 0 0 ZFA 1

ROC for σ2 N = σ2 SN 3 ZH 0 -3 -3 0 ZFA 3

What if both the mean and variance Change?

Alternative Sensitivity Measures Az: Area under the ROC (e. g. , see Swets, 1995, ch. 2 -3; Swets & Pickett, 1982) Range: from. 5— 1. 0 Underlying distributions can have unequal variances Assumes that the underlying distributions can be monotonically transformed to normality ZH= a + b. ZF

Area under the ROC

‘Non-parametric’ Measures: Sensitivity Not really non-parametric: No distribution assumed, but follows a logistic distribution (Macmillan & Creelman, 1990)

‘Non-parametric’ Measures: Response Bias For applications to vigilance, see See, Warm, Dember, & Howe (1997)

What if the Situation is More Complex? Response 1 State of the World 1 2 3 4 5 6 7

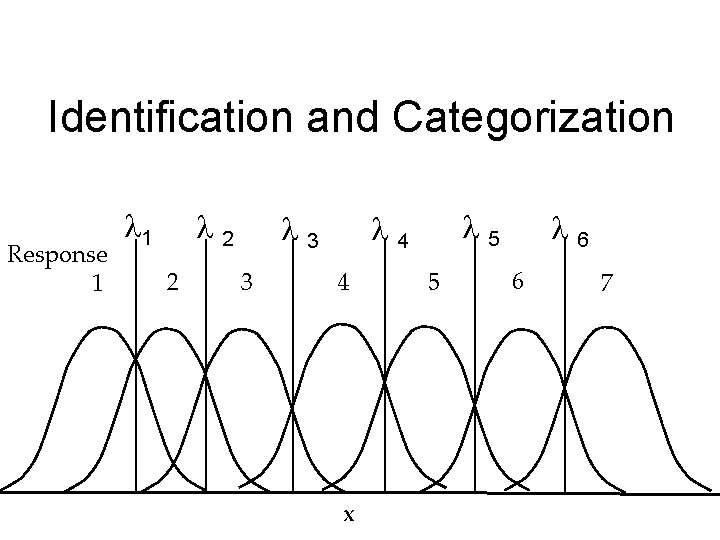
Identification and Categorization Response 1 1 2 2 3 5 4 3 4 x 5 6 6 7

Fuzzy Logic Traditional Set Theory: A∩A=0 Fuzzy Set Theory: A ∩ Ā ≠ 0 One assigns non-binary membership, or degrees of membership, to classes of events (fuzzification).

Elements of Fuzzy Signal Detection Theory ØEvents can belong to the set “signal” (s) to a degree ranging from 0 to 1 ØEvents can belong to the set “response” (r) to a degree ranging from 0 to 1

Computation of FSDT Measures Ø Select mapping functions for signal & response dimensions Ø Assignment of degrees of membership to the four outcomes (H, M, FA, CR) using mixed implication functions. Ø Compute fuzzy Hit, Miss, False Alarm, and Correct Rejection Rates Ø Compute detection theory measures of sensitivity and response bias

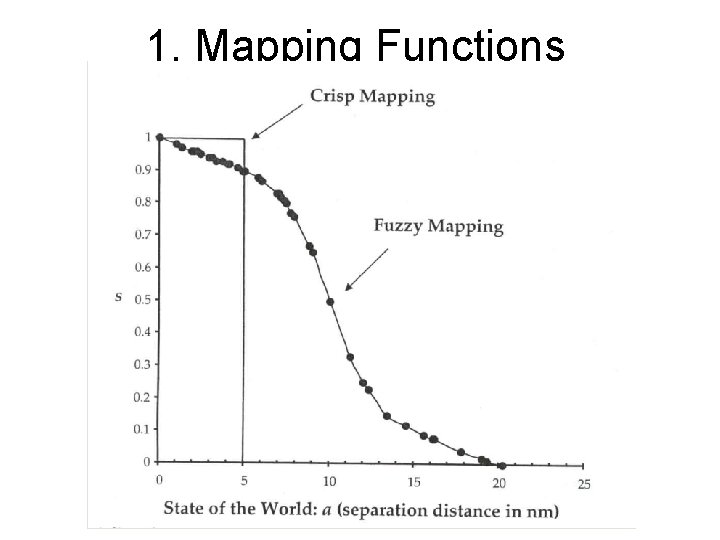
1. Mapping Functions

2. Assignment of Set Membership to Categories Mixed Implication Functions H = min (s, r) M = max (s-r, 0) FA = max (r-s, 0) CR = min (1 -s, 1 -r)

3. Computation of Fuzzy Hit and False Alarm Rate H= Σ(Hi)/ Σ(si) for i=1 to N M = Σ(Mi)/ Σ(si) for i =1 to N FA = Σ(FAi)/ Σ(1 -si) for i=1 to N CR = Σ(CRi)/ Σ(1 -si) for i= 1 to N

Truth Table for FSDT Data s. 83. 17 1. 00. 50 0. 83. 17. 67. 83 r 1. 00 0 1. 00. 50. 17. 50. 67 Hit. 83 0 1. 00. 50. 17. 50. 67 FA. 17 0 0 0 0 Miss 0. 17 0 0 0. 33 0. 17. 16 CR 0. 83 0. 50. 83. 17. 83. 33. 17

‘Perfect’ Performance s. 83. 17 1. 00. 50 0. 83 r 1. 00 0 1. 00. 50. 17. 50 Hit. 83 0 1. 00. 50 FA. 17 0 0 0. 17 0 Miss 0. 17 0 0 0. 33 C’R 0. 83 0. 50. 83. 17. 67. 83 . 17. 50. 67 0 0. 17. 16 . 83. 33. 17

‘Hitness’ and ‘False Alarmness’ s. 83. 17 1. 00. 50 0. 83. 17. 67. 83 r 1. 00 0 1. 00. 50. 17. 50. 67 Hit. 83 0 1. 00. 50. 17. 50. 67 FA. 17 0 0 0 0 Miss 0. 17 0 0 0. 33 0. 17. 16 CR 0. 83 0. 50. 83. 17. 83. 33. 17

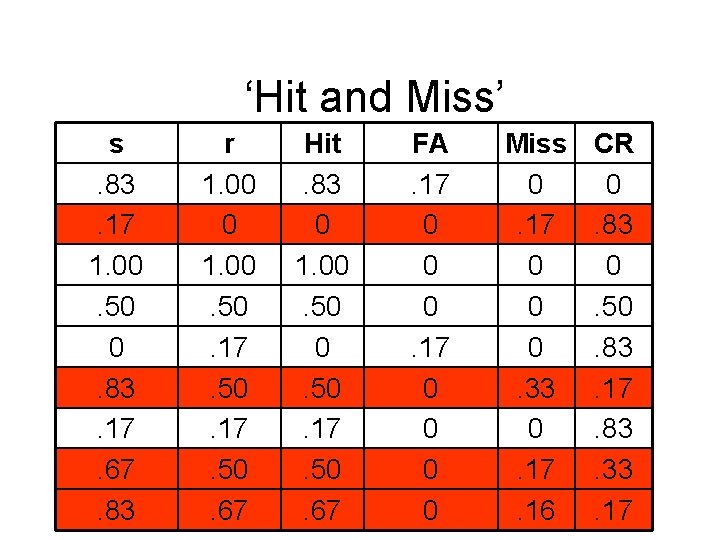
‘Hit and Miss’ s. 83. 17 1. 00. 50 0. 83. 17. 67. 83 r 1. 00 0 1. 00. 50. 17. 50. 67 Hit. 83 0 1. 00. 50. 17. 50. 67 FA. 17 0 0 0 0 Miss 0. 17 0 0 0. 33 0. 17. 16 CR 0. 83 0. 50. 83. 17. 83. 33. 17

Fuzzy Stimulus and Response: Duration Discrimination 1 2 3 4 5 6 7 20 msec 200 220 240 260 280 300 320 80 msec 200 280 360 440 520 600 680

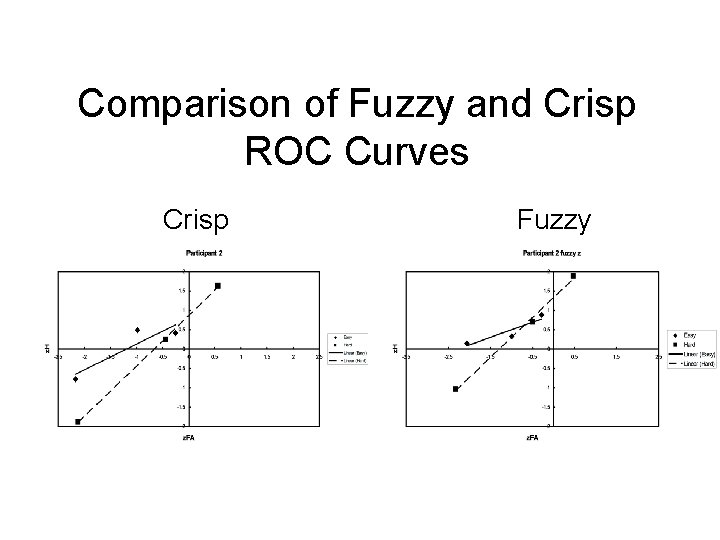
Comparison of Fuzzy and Crisp ROC Curves Crisp Fuzzy

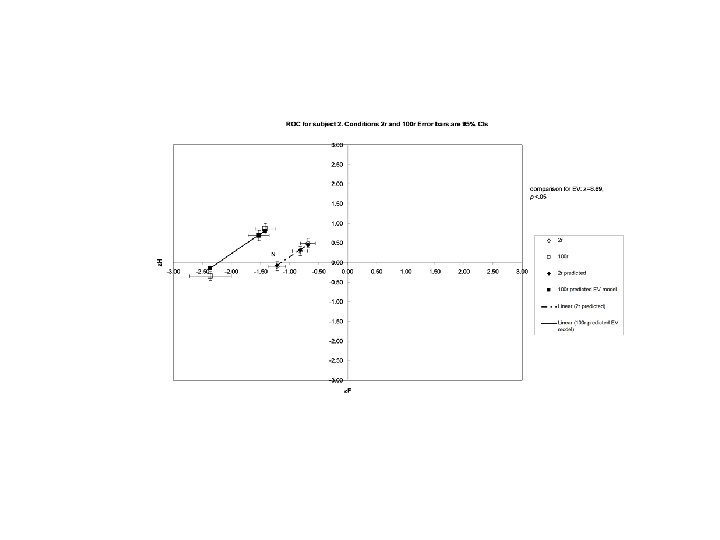
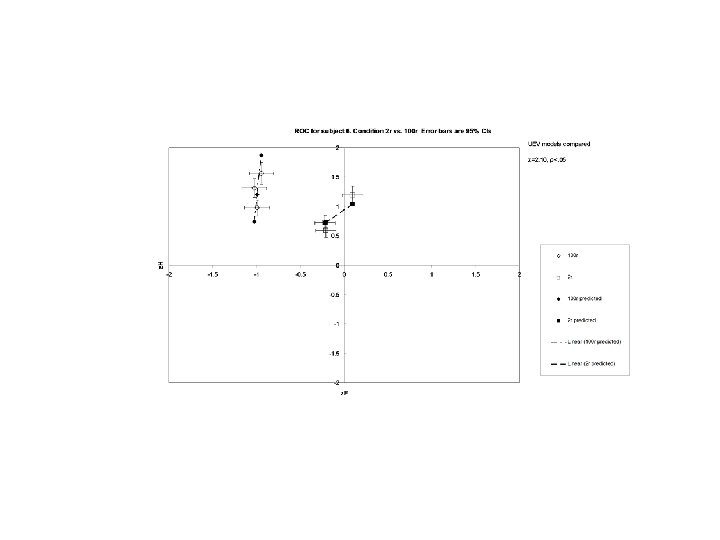
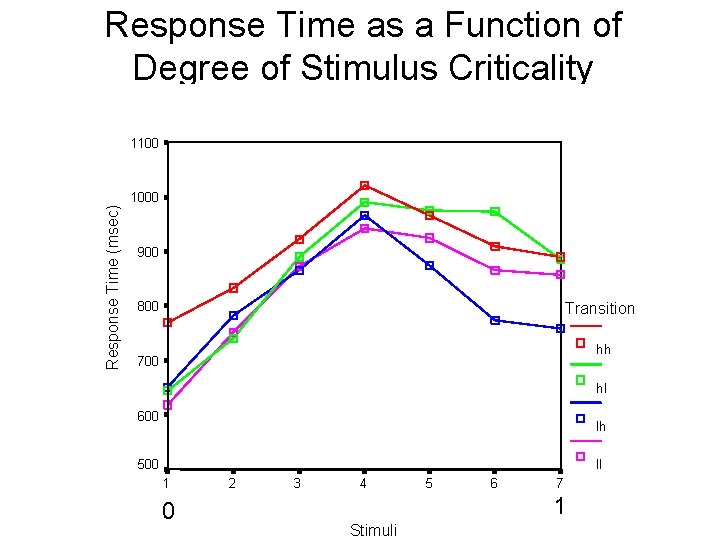
Response Time as a Function of Degree of Stimulus Criticality 1100 Response Time (msec) 1000 900 800 Transition hh 700 hl 600 lh 500 ll 1 0 2 3 4 5 6 7 1 Stimuli

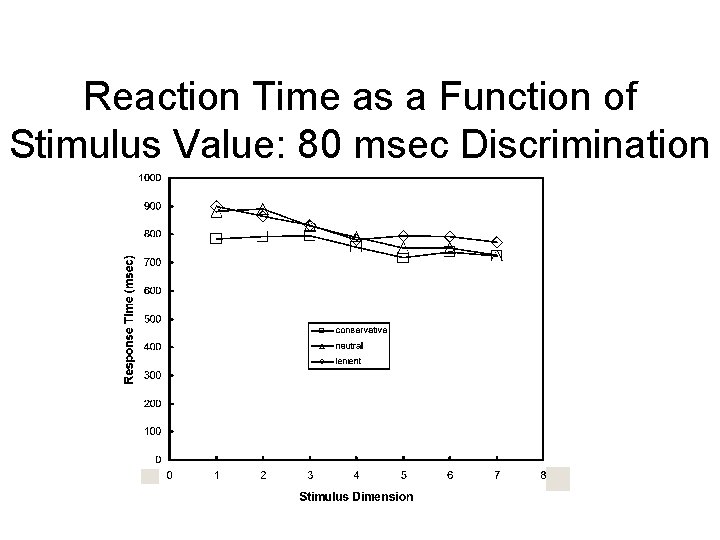
Reaction Time as a Function of Stimulus Value: 80 msec Discrimination

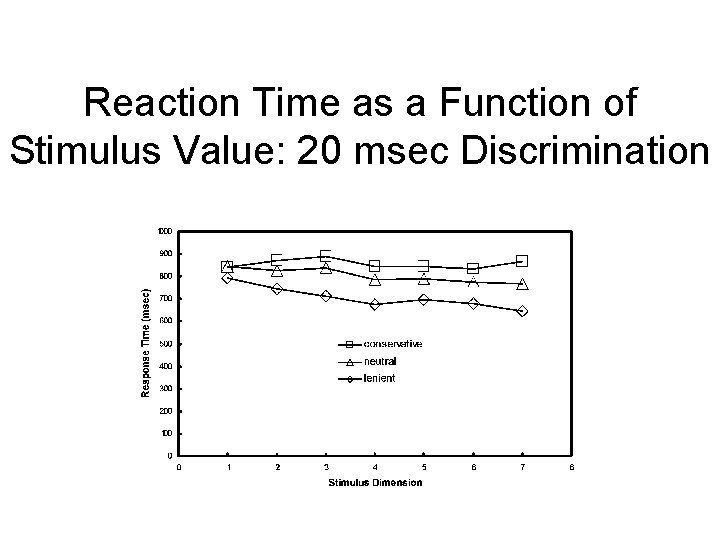
Reaction Time as a Function of Stimulus Value: 20 msec Discrimination