Original Synteny Vincent Ferretti Joseph H Nadeau David

Original Synteny Vincent Ferretti, Joseph H. Nadeau, David Sankoff, 1996 Presented by: Suzy Sun

Synteny: Two genes are syntenic if they are assigned to the same chromosome

Introduction • We know more about chomosomal gene assignment rather than where exactly these genes are located on the chromosome • Comparing species without chromosomal maps becomes a question of comparing syntenic sets of genes while disregarding gene order or gene orientation • Only interchromosomal events (translocation, fusion, and fission) affect synteny and can thus be deduced from synteny data

Motivation Using the synteny data of present-day organisms… • What can we infer about synteny sets of their ancestors? • How many chromosomes did these ancestors possess and what genes did they contain?

Problems 1. Calculate syntenic edit distance between 2 genomes by inferring number of translocations, fusions, and fissions 2. Use calculated distance to analyze the median problem for synteny i. e. find the genome with minimized sum of distances to three given genomes 3. Optimize internal vertices of a given phylogenetic tree

Problem 1 Calculate syntenic edit distance between 2 genomes by inferring number of translocations, fusions, and fissions

Syntenic Distance Genome 1 Chromosome 1: {x, y} Chromosome 2: {p, q, r} Chromosome 3: {a, b, c} Genome 2 Chromosome 1: {p, q, x} Chromosome 2: {a, b, r, y, z} Compact Representation: {1, 2}, {1, 2, 3}

Syntenic Distance Solution: Find the series of translocations, fusions, and fissions that transform Genome 2 into the k chromosomes of Genome 1 i. e. {1}, {2}, … , {k} {1, 2}, {1, 2, 3} transformed by translocation to {1}, {2, 3} transformed by fission to {1}, {2}, {3} Distance = 2

Syntenic Distance for r(l)=1 Suppose l appears in r(l) chromosomes in Genome 2 If r(l)=1 and syntenic labels of l (l’) do not appear in any other chromosome, effect a fission to produce {l} as an individual chromosome If r(l)=1 and all labels l’ appear in r(l’)>rmin>1 chromosomes, effect a translocation to produce {l}

Example {1, 2, 3, 4}, {2, 3, 5}, {2, 3, 4}, {4, 5, 6}, {4, 8, 9} Choose l=1 then, r(l)=1 rmin=3 l’=2 or l’=3 If {2, 3, 4} is the second chromosome in the translocation with {1, 2, 3, 4} then we get, {1}, {2, 3, 4}, {2, 3, 5}, {4, 5, 6}, {4, 8, 9}

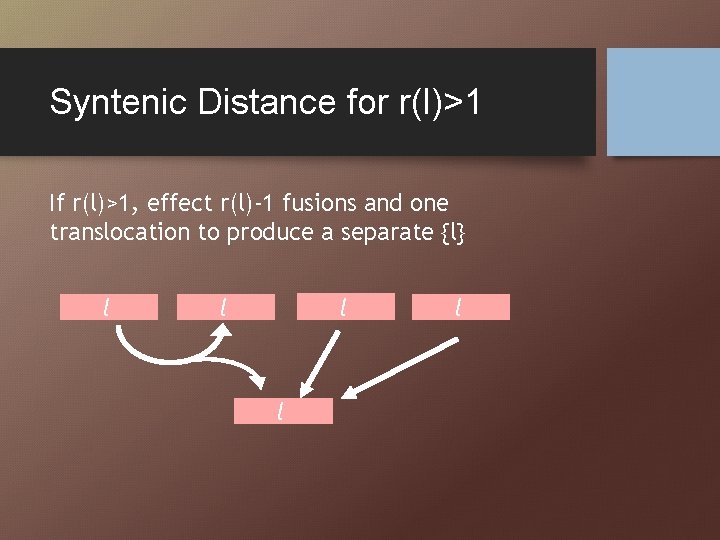
Syntenic Distance for r(l)>1 If r(l)>1, effect r(l)-1 fusions and one translocation to produce a separate {l} l l l

How do we know which l to choose? 1. Any l for which r(l)=1 2. Any l for which r(l)=2 3. If all r(l)>2, choose l that minimizes r(l) and r(l’)

Simulations and Tests If the algorithm indeed yields the true minimum distance, then converting Genome 1 to Genome 2 should equal the distance from Genome 2 to Genome 1 • 65% identical in both directions • 34% differed by 1 • 1% differed by 2 or more

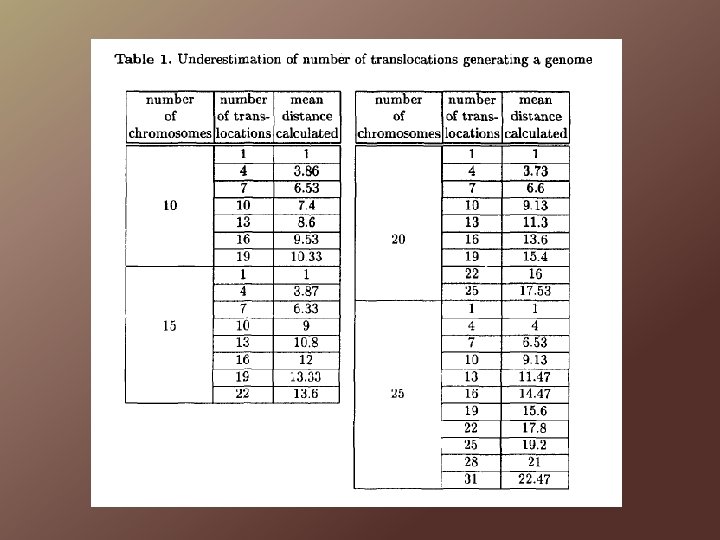
Simulations and Tests Testing the application of syntenic distance to evolutionary history Generate random genomes by inducing a number of random translocations to {1}, …, {k} chromosomes When number of translocations < k/2, the algorithm yields the correct number of translocations, but as the number of translocations increase, the algorithm underestimates the true distance

Problem 2 Use calculated distance to analyze the median problem for synteny i. e. find the genome with minimized sum of distances to three given genomes

The Median Problem Let d(Genome 1, Genome 2) be the syntenic distance between Genome 1 and Genome 2 Median problem: given three genomes 1, 2, and 3, construct a genome S so that d(S, 1) + d(S, 2) + d(S, 3) is minimized

Median Content Constraint (MCC) Genome S must contain certain genes present in all genomes 1, 2, and 3 OR two out of three genomes OR even in any of the three genomes Bottom-line: S cannot be empty, otherwise, the sum of the three distances is 0, and thus trivial

The Median Problem 1. Choose any gene to be in S according to the MCC. The initial chromosome in S contains this one gene. 2. If there are unassigned genes that fulfill the MCC, they are added only if they do not increase the current cost. Otherwise, we assign genes based on whichever minimizes the sum of the distances to terminal nodes. 3. Perform iterations that rearrange each gene into a different chromosome and compute the sum of the three distances until the minimum distance is reached.

Problem 3 Optimize internal vertices of a given phylogenetic tree

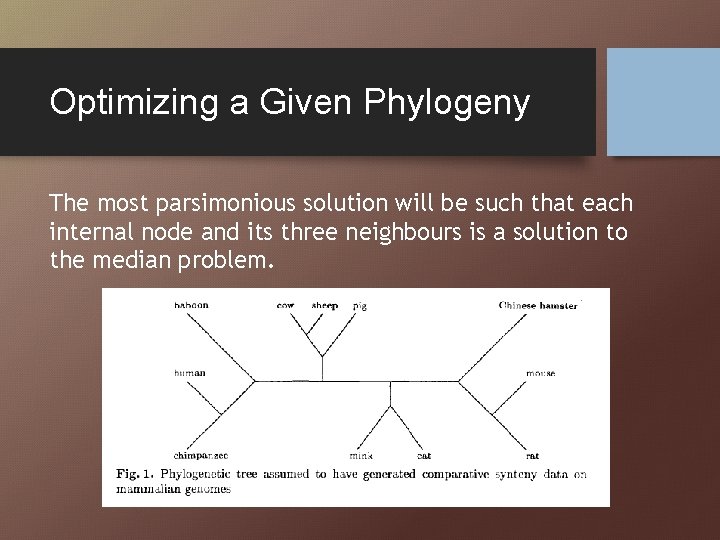
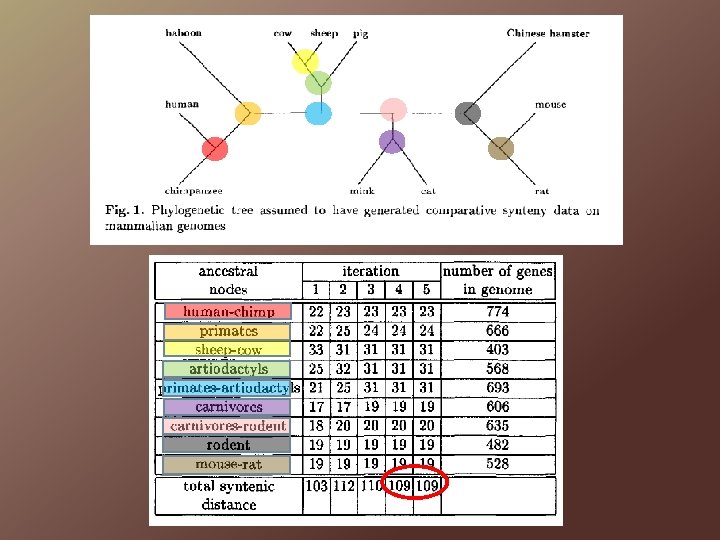
Optimizing a Given Phylogeny The most parsimonious solution will be such that each internal node and its three neighbours is a solution to the median problem.

Optimizing a Given Phylogeny MCC: ‘…include those genes in only one of the three genomes if they can be added after all the other genes are assigned chromosomes, in only one cost-free way. ’

Limitations and Conclusions • To find the most parsimonious tree we would have to compute all possible trees and their total syntenic distances (not computationally feasible at the time) • But syntenic distance useful for comparing competing hypotheses

Conclusions

Thank you