Organisasi Sistem Komputer Materi III Binary Digit Number

Organisasi Sistem Komputer Materi III Binary Digit (Number System)

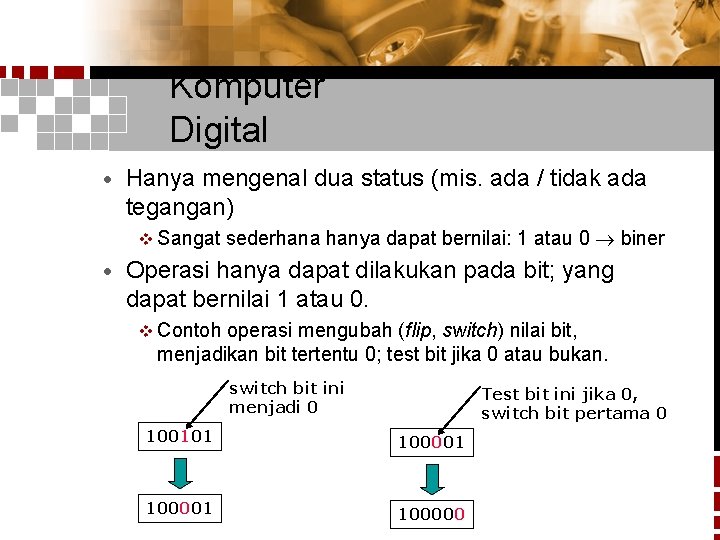
Komputer Digital · Hanya mengenal dua status (mis. ada / tidak ada tegangan) v Sangat · sederhana hanya dapat bernilai: 1 atau 0 biner Operasi hanya dapat dilakukan pada bit; yang dapat bernilai 1 atau 0. v Contoh operasi mengubah (flip, switch) nilai bit, menjadikan bit tertentu 0; test bit jika 0 atau bukan. switch bit ini menjadi 0 Test bit ini jika 0, switch bit pertama 0 100101 100001 100000

Binary Digit (Bit) § Dengan bit, bagaimana komputer dapat merepresentasikan: Bilangan (numerik)? Alfabet ? Kata? Alamat? Gambar? · Contoh: Bilangan · v Manusia lebih mudah menggunakan representasi/ notasi desimal. v Misalkan: 1, 25, 125, 3896754321 v Disebut basis 10, dengan simbol: Digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 § Komputer hanya mengenal 2 simbol (0 dan 1) Bagaimana komputer merepresentasikan

Representasi Bit § Bits dapat merepresentasikan apapun! · Karakter Latin: v 26 huruf => 5 bits v. Huruf besar/kecil + tanda lain => 7 bits, · Logical values : v 0 -> False, 1 => True · Warna ? Berapa banyak warna => berapa bits? · Alamat? (berapa karakter alfabet. . ) § Maka N bits hanya dapat merepresentasikan 2 N sesuatu

Bit Bilangan § Bilangan Basis B B simbol per digit: · Basis 10 (Decimal): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Basis 2 (Binary): 0, 1 § Komputer menyimpan dan beroperasi dalam “binary” Basis 2 Dapat melakukan konversi (representasi) bilangan dari basis 10 ke basis 2 (dan sebaliknya). · Decimal: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 · 90 = 9 x 101 + 0 x 100 · Binary: 0, 1 1011010 = 1 x 26 + 0 x 25 + 1 x 24 + 1 x 23 + 0 x 22 + 1 x 2 + 0 x 20 = 64 + 16 + 8 +2 = 90

Bit Bilangan § Apa yang dapat dilakukan dengan “bilangan”? · semua operasi (instruksi) yang biasa dilakukan pada bilangan! v. Tambahkan, Bandingkan! Kurangkan, Kalikan, Bagikan, 1 · Contoh: 10 + Bagaimana instruksi +, diwakili oleh bits? 1 7 = 17 + 0 1 0 10 1 1 1 7 ------------1 0 0 0 1 17

Bit Instruksi § Instruksi (Operasi). Apakah dapat diwakili oleh bit? · Contoh: v 0 => tepuk tangan v 1 => snap jari jempol dan telunjuk v Eksekusi Instruksi: 1 0 1 1 0 0 § Contoh instruksi operasi bilangan: · Misalkan 3 bit (berapa banyak instruksi? ): v 000 => tambahkan 001 => kurangkan v 010 => kalikan 011 => bagikan v 100 => bandingkan dst. § Jadi bit (data) dapat diartikan sebagai instruksi!

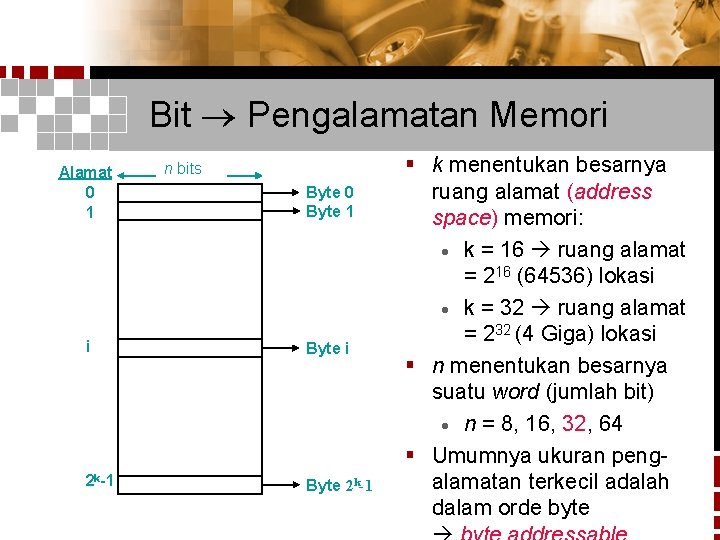
Bit Pengalamatan Memori Alamat 0 1 n bits Byte 0 Byte 1 i Byte i 2 k-1 Byte 2 k-1 § k menentukan besarnya ruang alamat (address space) memori: · k = 16 ruang alamat = 216 (64536) lokasi · k = 32 ruang alamat = 232 (4 Giga) lokasi § n menentukan besarnya suatu word (jumlah bit) · n = 8, 16, 32, 64 § Umumnya ukuran pengalamatan terkecil adalah dalam orde byte

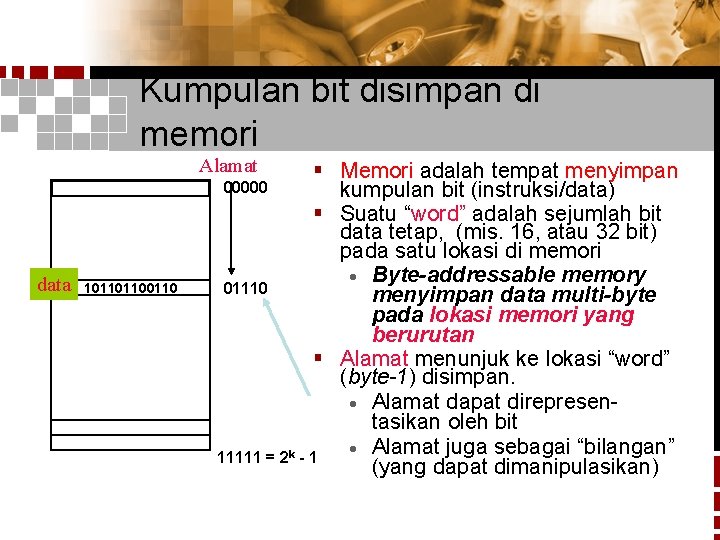
Kumpulan bit disimpan di memori Alamat data 10110110 § Memori adalah tempat menyimpan 00000 kumpulan bit (instruksi/data) § Suatu “word” adalah sejumlah bit data tetap, (mis. 16, atau 32 bit) pada satu lokasi di memori · Byte-addressable memory 01110 menyimpan data multi-byte pada lokasi memori yang berurutan § Alamat menunjuk ke lokasi “word” (byte-1) disimpan. · Alamat dapat direpresentasikan oleh bit · Alamat juga sebagai “bilangan” 11111 = 2 k - 1 (yang dapat dimanipulasikan)

Pengalamatan Data: Endianess Pengalamatan data multi-byte adalah: § Big Endian: alamat dari most significant byte · IBM 360/370, Motorola 68 k, MIPS, Sparc, HP PA lsb 0 msb 4 1 5 0 0 § Little Endian: alamat dari least significant byte · Intel 80 x 86, DEC Vax, DEC Alpha 0 lsb 4 0 msb 0 5 1

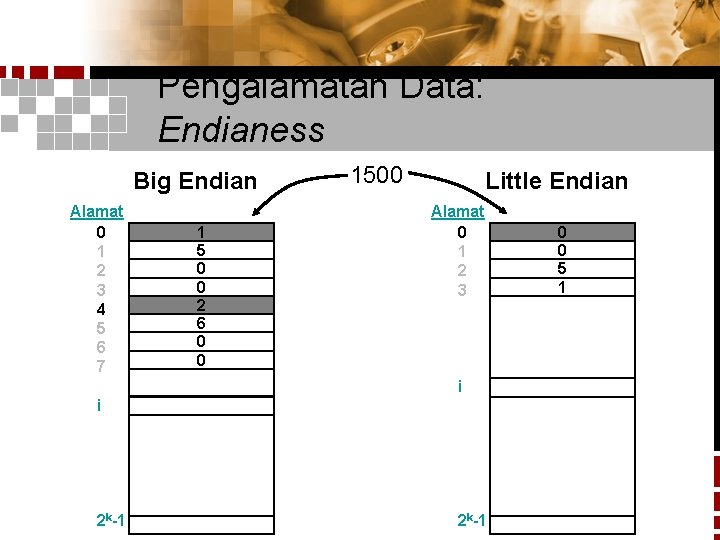
Pengalamatan Data: Endianess Big Endian Alamat 0 1 2 3 4 5 6 7 1 5 0 0 2 6 0 0 1500 Little Endian Alamat 0 1 2 3 i i 2 k-1 0 0 5 1

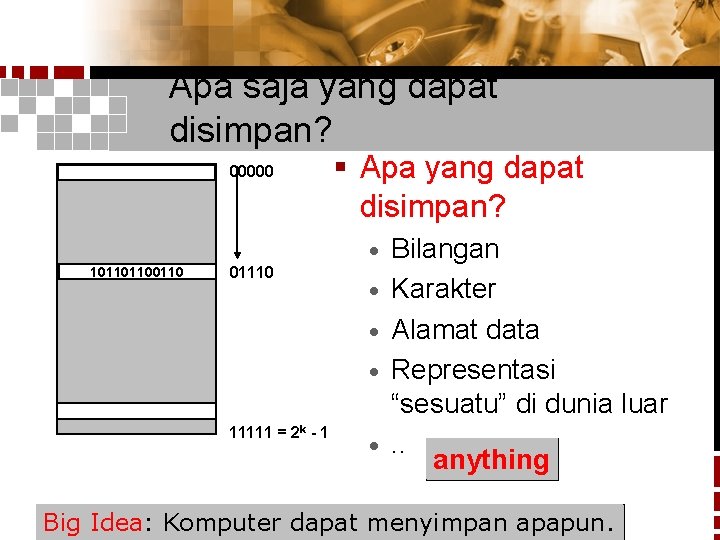
Apa saja yang dapat disimpan? 00000 § Apa yang dapat disimpan? · 10110110 01110 · · · 11111 = 2 k - 1 · Bilangan Karakter Alamat data Representasi “sesuatu” di dunia luar. . anything Big Idea: Komputer dapat menyimpan apapun.

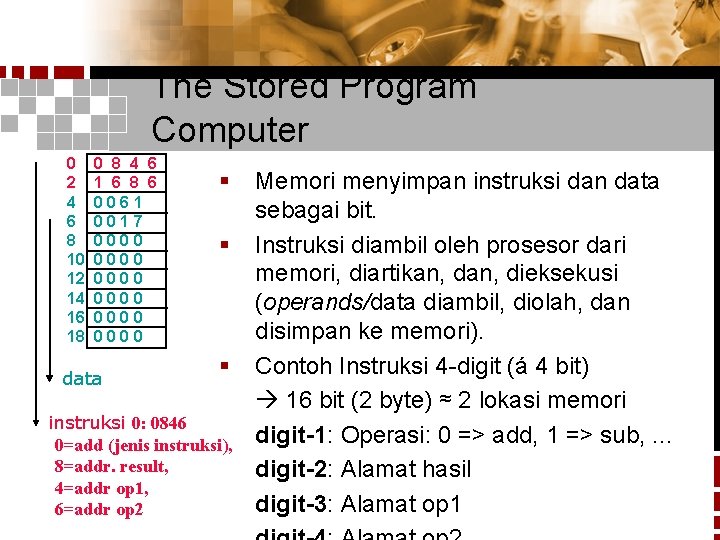
The Stored Program Computer 0 2 4 6 8 10 12 14 16 18 0 8 4 6 1 6 8 6 0061 0017 0000 0000 data § § § instruksi 0: 0846 0=add (jenis instruksi), 8=addr. result, 4=addr op 1, 6=addr op 2 Memori menyimpan instruksi dan data sebagai bit. Instruksi diambil oleh prosesor dari memori, diartikan, dieksekusi (operands/data diambil, diolah, dan disimpan ke memori). Contoh Instruksi 4 -digit (á 4 bit) 16 bit (2 byte) ≈ 2 lokasi memori digit-1: Operasi: 0 => add, 1 => sub, . . . digit-2: Alamat hasil digit-3: Alamat op 1

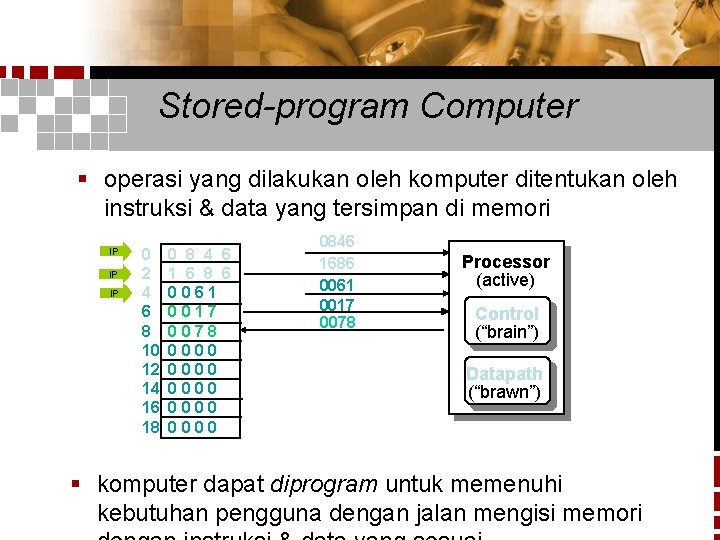
Stored-program Computer § operasi yang dilakukan oleh komputer ditentukan oleh instruksi & data yang tersimpan di memori IP IP IP 0 2 4 6 8 10 12 14 16 18 0 8 4 6 1 6 8 6 0061 0017 007 08 0 0000 0000 0846 1686 0061 0017 0078 Processor (active) Control (“brain”) Datapath (“brawn”) § komputer dapat diprogram untuk memenuhi kebutuhan pengguna dengan jalan mengisi memori

Representasi Data : Bilangan Biner § Harga/Nilai suatu bilangan biner: 1011010 = 1 x 26 + 0 x 25 + 1 x 24 + 1 x 23 + 0 x 22 + 1 x 21 + 0 x 20 = 64 + 16 + 8 +2 = 90 Penulisan: 1011010 b § Konversi: Desimal Biner 90 / 2 = 45 sisa 0 45 / 2 = 22 sisa 1 22 / 2 = 11 sisa 0 11 / 2 = 5 sisa 1 5 / 2 = 2 sisa 1

Bilangan Heksa-Desimal § Simbol: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F § Harga/Nilai suatu bilangan heksa-desimal: 5 A = 5 x 161 + 10 x 160 = 80 + 10 = 90 Penulisan: 5 Ah atau 0 x 5 A § Konversi: Desimal Heksa-desimal 90 / 16 = 5 sisa 10 (A) 5 / 16 = 0 sisa 5 § Konversi: Heksa-desimal Biner 5 A = 1010 § Konversi: Biner Heksa-desimal 1011010 = 5 A = 5 A

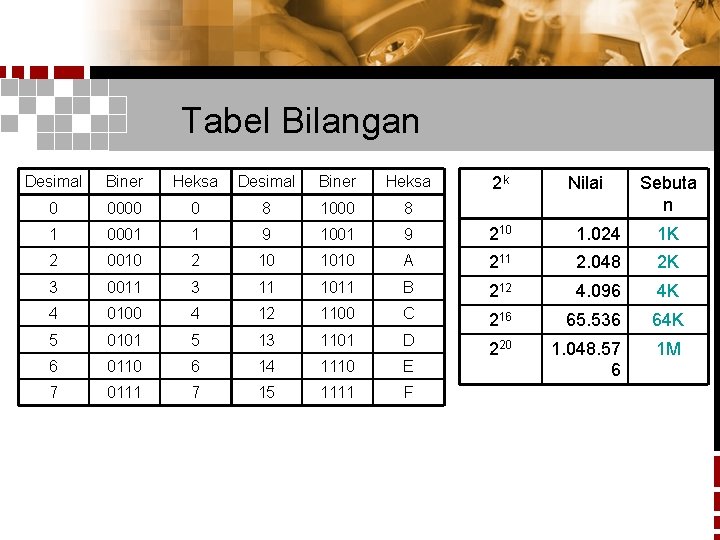
Tabel Bilangan Desimal Biner Heksa 0 0000 0 8 1000 8 1 0001 1 9 1001 9 210 1. 024 1 K 2 0010 2 10 1010 A 211 2. 048 2 K 3 0011 3 11 1011 B 212 4. 096 4 K 4 0100 4 12 1100 C 216 65. 536 64 K 5 0101 5 13 1101 D 6 0110 6 14 1110 E 220 1. 048. 57 6 1 M 7 0111 7 15 1111 F 2 k Nilai Sebuta n

Pengelompokkan Bit § Bit String: INTEL MIPS · 4 bit nibble · 8 bit byte · 16 bit word half-word · 32 bit double-word · 64 bit quad-word double-word § Alamat lokasi memori · umumnya dinyatakan dengan bilangan heksa desimal · contoh: v lokasi memori 90 pada memori dengan ruang memori sebesar 64 K (65536 = 216) dinyatakan dengan alamat: 0 x 005 A v jika ruang memori sebesar 232 (4 G) : 0 x 0000005 A

Penyimpanan data multi-byte (Little Endian) int i = 90; i 90 = 0 x 5 A = 0000 0000 0101 1010 int j = 987700; j 00000001 00000002 00000003 00000004 00000005 00000006 00000007 0101 1010 0000 0000 0011 0100 0001 0010 0000 1111 0000 987700 = 0 x 000 F 1234 = 0000 1111 0001 0010 0011 0100 FFFF Alamat Memori (32 bit) Kapasitas Memori (8 bit)

One-Bit Full Adder § Example Binary Addition: a: 0 b: 0 Sum: 1 0 1 0 0 1 Carries 1 0 § Thus for any bit of addition: · The inputs are ai, bi, Carry. Ini · The outputs are Sumi, Carry. Outi § Note: Carry. Ini+1 = Carry. Outi

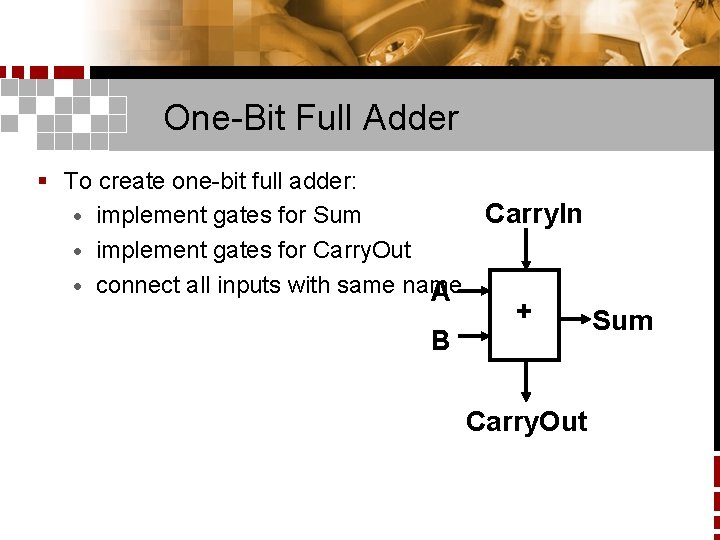
One-Bit Full Adder § To create one-bit full adder: Carry. In · implement gates for Sum · implement gates for Carry. Out · connect all inputs with same name A B + Carry. Out Sum

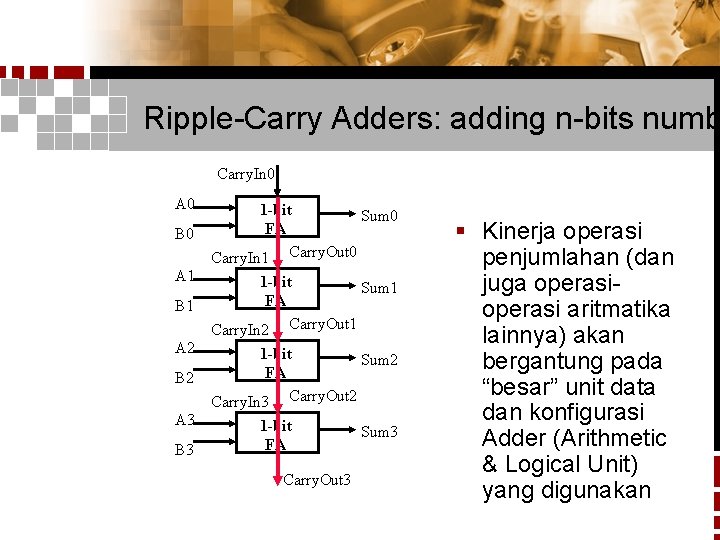
Ripple-Carry Adders: adding n-bits numb Carry. In 0 A 0 B 0 A 1 B 1 A 2 B 2 A 3 B 3 1 -bit Sum 0 FA Carry. In 1 Carry. Out 0 1 -bit Sum 1 FA Carry. In 2 Carry. Out 1 1 -bit Sum 2 FA Carry. In 3 Carry. Out 2 1 -bit FA Carry. Out 3 Sum 3 § Kinerja operasi penjumlahan (dan juga operasi aritmatika lainnya) akan bergantung pada “besar” unit data dan konfigurasi Adder (Arithmetic & Logical Unit) yang digunakan

How to Represent Negative Numbers? § So far, unsigned numbers § Obvious solution: define leftmost bit to be sign! 0 => +, 1 => · Rest of bits can be numerical value of number · § Representation called sign and magnitude 0000 0011 = + 3 1000 0011 = - 3

Another try: complement the bits § Example: 710 = 001112 -710 = 110002 § Called one’s Complement § Note: positive numbers have leading 0 s, negative numbers have leadings 1 s. 00000 100001 . . . 11110 11111 § What is -00000 ? § How many positive numbers in N bits? § How many negative ones? . . . 01111

Two’s Complement Number line 111110 -2 00000 -1 0 000010 1 2 . . . -15 -16 15 10001 10000 01111 § 2 N-1 nonnegatives § 2 N-1 negatives § one zero § how many positives? § comparison? § overflow?

Addition & Subtraction Operations § Subtraction: § Addition: Just add the two numbers · Ignore the Carry-out from MSB · Result will be correct, provided there’s no overflow · Form 2’s complement of the subtrahend · Add the two numbers as in Addition · 0 1 (+5) +0 0 1 0 (+2) 0 1 1 1 (+7) 0 1 (+5) +1 0 (-6) 1 1 (-1) 0 0 1 0 (+2) 0 1 0 0 (+4) 1 0 1 1 (-5) +1 1 1 0 (-2) 11 0 0 1 (-7) 0 1 1 1 (+7) +1 1 0 1 (-3) 10 1 0 0 (+4) 1 1 1 0 (-2) 1 0 1 1 (-5) 0010 +1 1 0 0 (-4) 1 1 1 0 (-2) 1110 +0 1 (+5) 10 0 1 1 (+3)

Overflow Decimal 0 1 2 3 4 5 6 7 Binary 0000 0001 0010 0011 0100 0101 0110 0111 Decimal 0 -1 -2 -3 -4 -5 -6 -7 -8 2’s Complement 0000 1111 1110 1101 1100 1011 1010 1001 1000 § Examples: 7 + 3 = 10 but. . . § - 4 – 5 = - 9 but. . . 0 + 1 1 0 1 1 1 0 0 1 1 7 3 1 0 – 6 + 1 1 0 0 1 1 – 4 – 5 0 1 1 1 7