Ordinary LeastSquares Outline Linear regression Geometry of leastsquares

Ordinary Least-Squares

Outline • Linear regression • Geometry of least-squares • Discussion of the Gauss-Markov theorem Ordinary Least-Squares

One-dimensional regression Ordinary Least-Squares

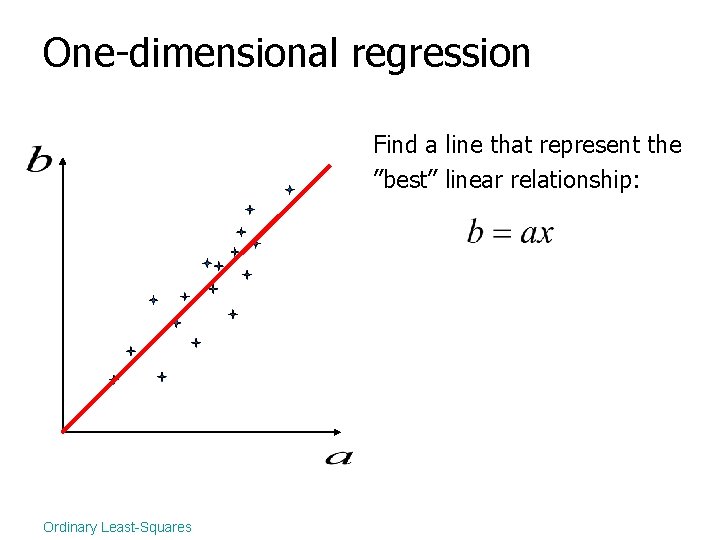
One-dimensional regression Find a line that represent the ”best” linear relationship: Ordinary Least-Squares

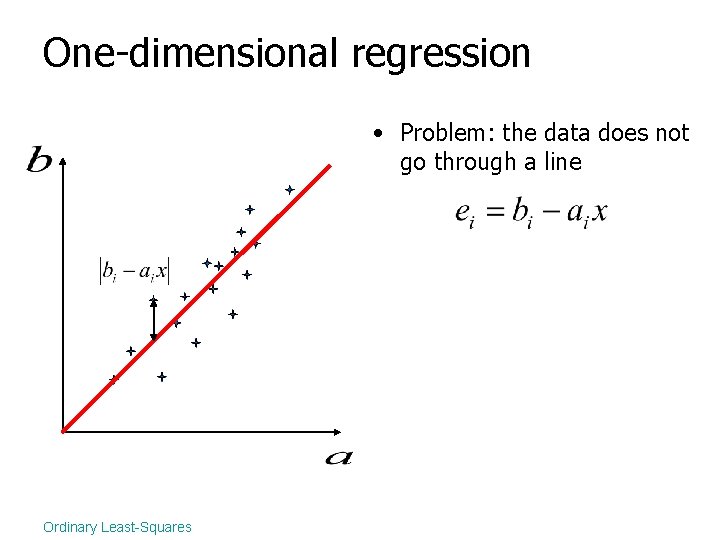
One-dimensional regression • Problem: the data does not go through a line Ordinary Least-Squares

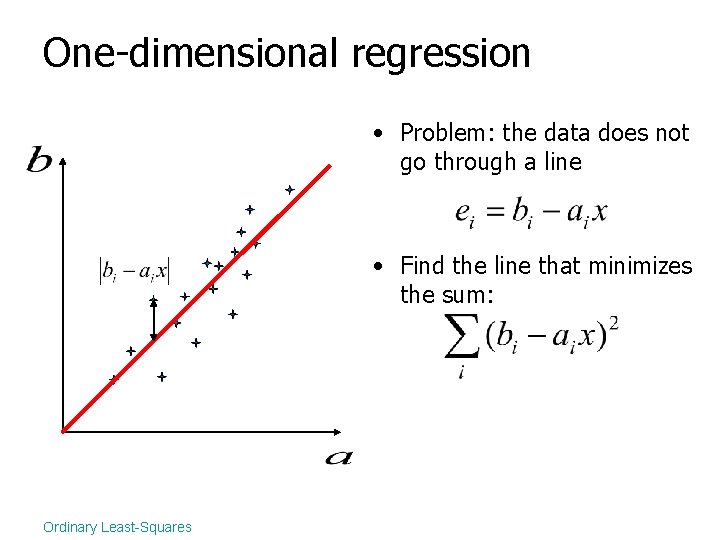
One-dimensional regression • Problem: the data does not go through a line • Find the line that minimizes the sum: Ordinary Least-Squares

One-dimensional regression • Problem: the data does not go through a line • Find the line that minimizes the sum: • We are looking for minimizes Ordinary Least-Squares that

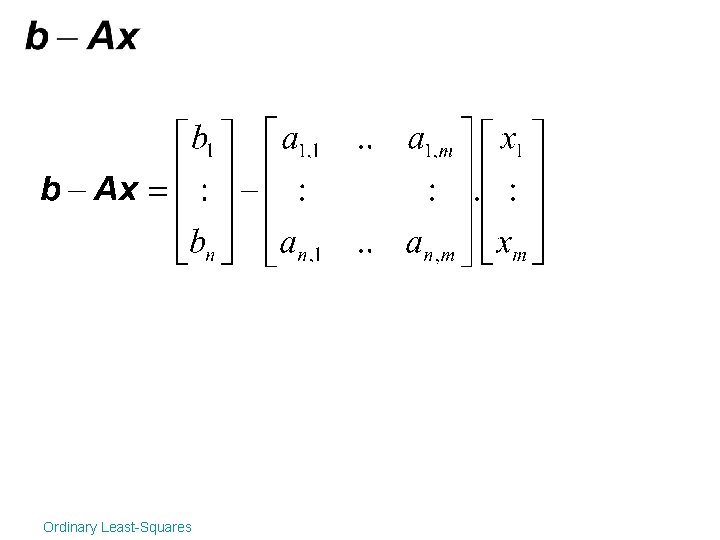
Matrix notation Using the following notations and Ordinary Least-Squares

Matrix notation Using the following notations and we can rewrite the error function using linear algebra as: Ordinary Least-Squares

Matrix notation Using the following notations and we can rewrite the error function using linear algebra as: Ordinary Least-Squares

Multidimentional linear regression Using a model with m parameters Ordinary Least-Squares

Multidimentional linear regression Using a model with m parameters Ordinary Least-Squares

Multidimentional linear regression Using a model with m parameters Ordinary Least-Squares

Multidimentional linear regression Using a model with m parameters and n measurements Ordinary Least-Squares

Multidimentional linear regression Using a model with m parameters and n measurements Ordinary Least-Squares

Ordinary Least-Squares

Ordinary Least-Squares

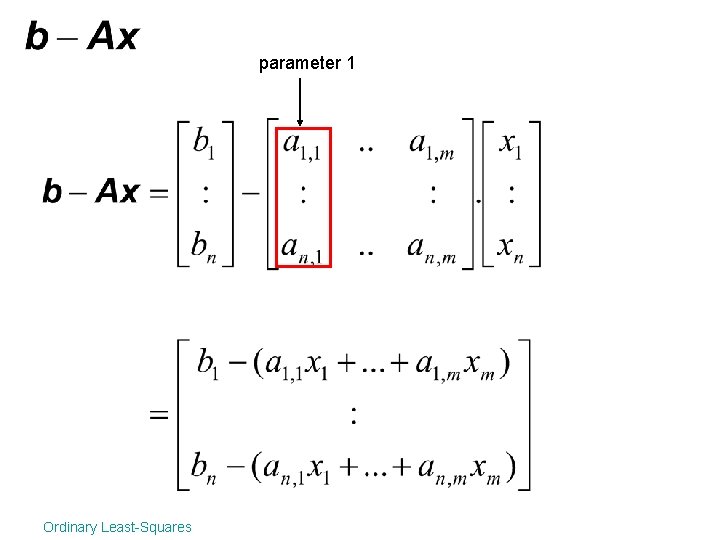
parameter 1 Ordinary Least-Squares

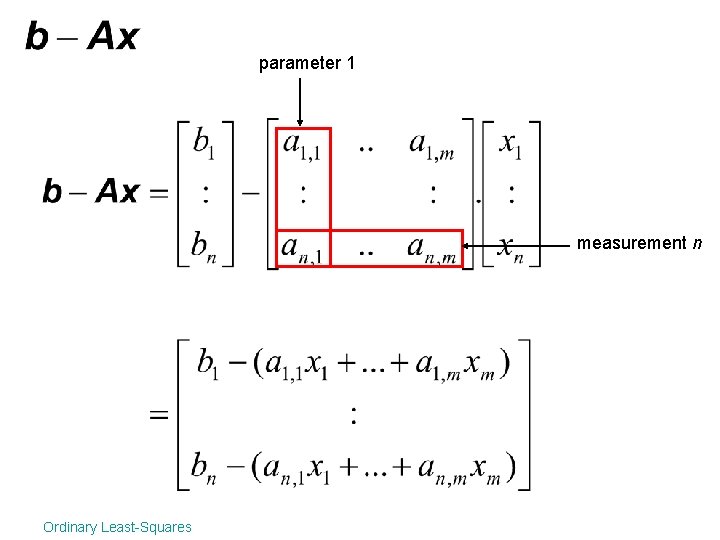
parameter 1 measurement n Ordinary Least-Squares

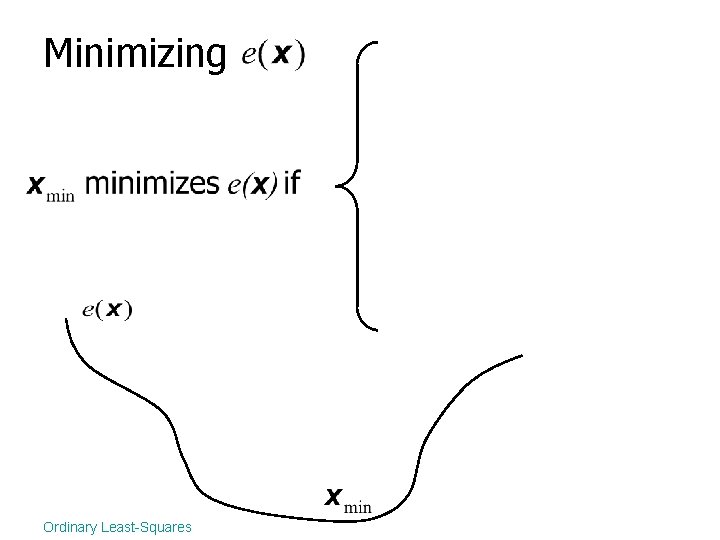
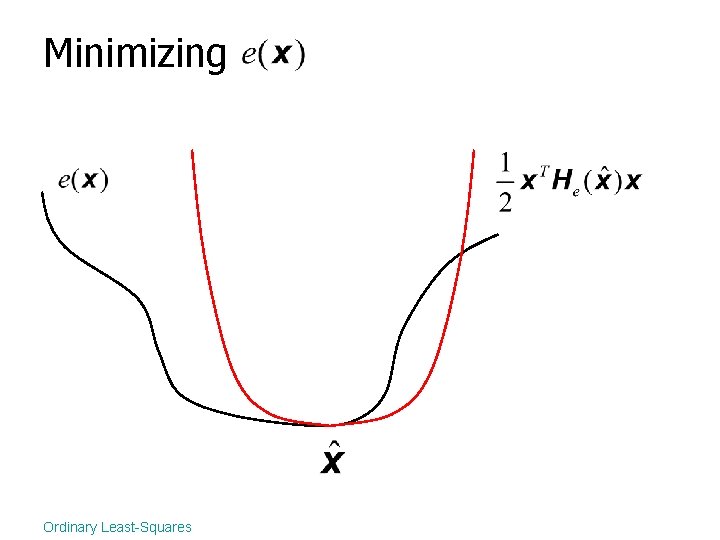
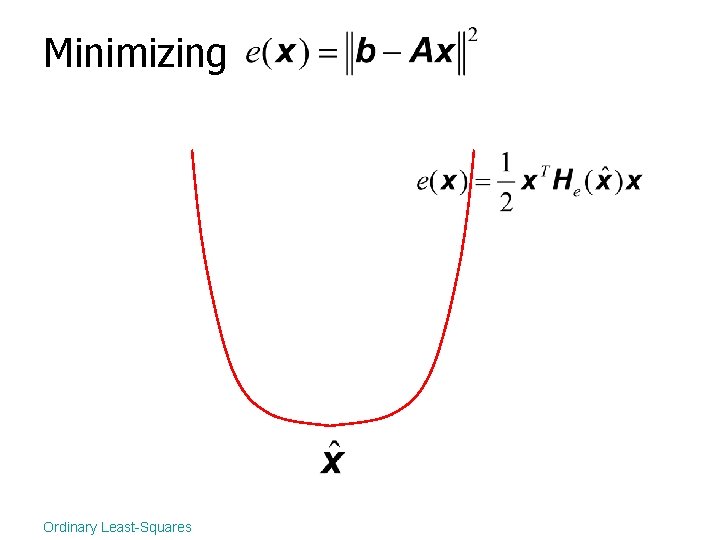
Minimizing Ordinary Least-Squares

Minimizing Ordinary Least-Squares

Minimizing Ordinary Least-Squares is flat at

Minimizing Ordinary Least-Squares is flat at

Minimizing is flat at does not go down around Ordinary Least-Squares

Minimizing is flat at does not go down around Ordinary Least-Squares

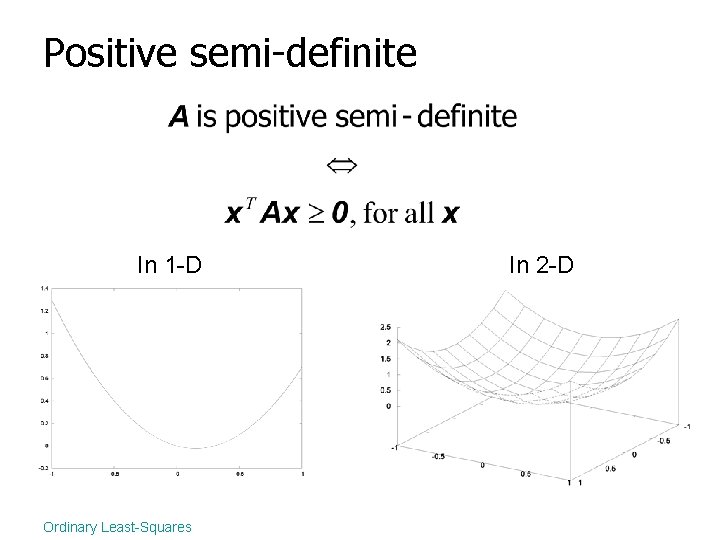
Positive semi-definite In 1 -D Ordinary Least-Squares In 2 -D

Minimizing Ordinary Least-Squares

Minimizing Ordinary Least-Squares

Minimizing Ordinary Least-Squares

Minimizing Always true Ordinary Least-Squares

Minimizing The normal equation Always true Ordinary Least-Squares

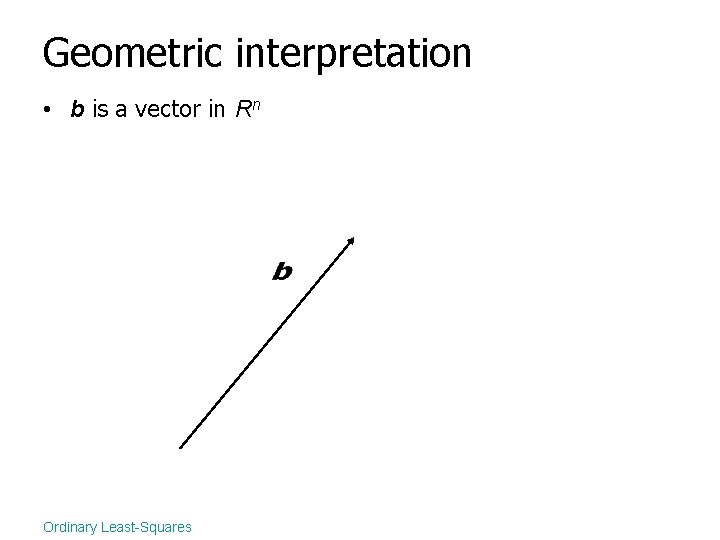
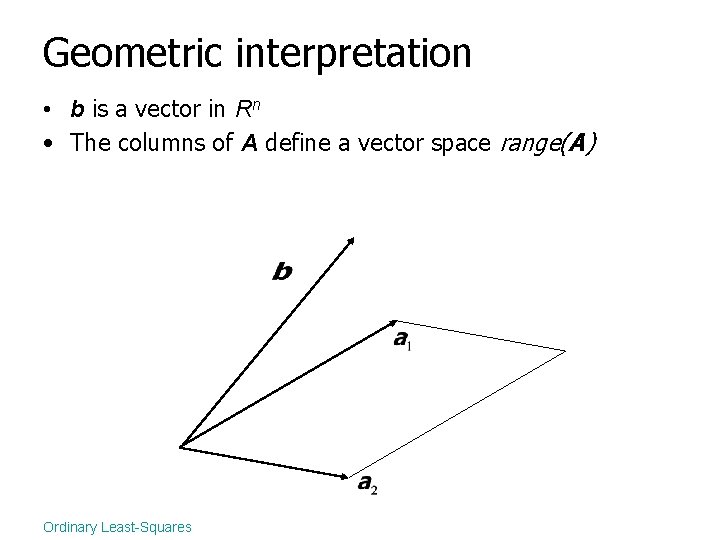
Geometric interpretation Ordinary Least-Squares

Geometric interpretation • b is a vector in Rn Ordinary Least-Squares

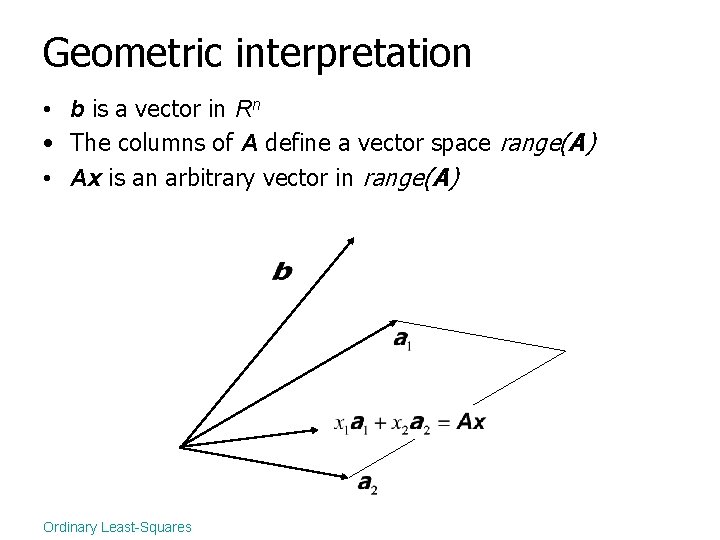
Geometric interpretation • b is a vector in Rn • The columns of A define a vector space range(A) Ordinary Least-Squares

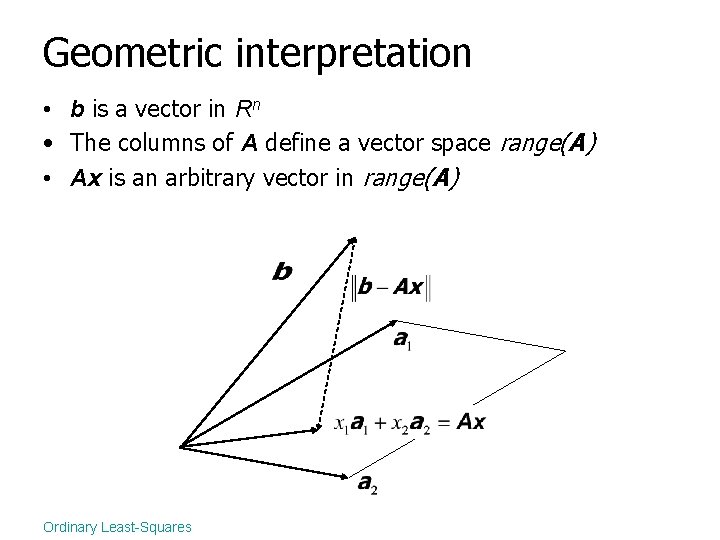
Geometric interpretation • b is a vector in Rn • The columns of A define a vector space range(A) • Ax is an arbitrary vector in range(A) Ordinary Least-Squares

Geometric interpretation • b is a vector in Rn • The columns of A define a vector space range(A) • Ax is an arbitrary vector in range(A) Ordinary Least-Squares

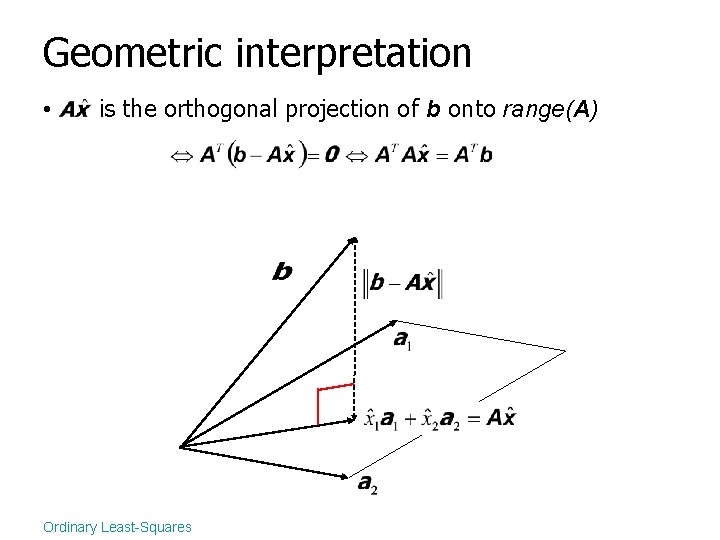
Geometric interpretation • is the orthogonal projection of b onto range(A) Ordinary Least-Squares

The normal equation: Ordinary Least-Squares

The normal equation: • Existence: Ordinary Least-Squares has always a solution

The normal equation: • Existence: has always a solution • Uniqueness: the solution is unique if the columns of A are linearly independent Ordinary Least-Squares

The normal equation: • Existence: has always a solution • Uniqueness: the solution is unique if the columns of A are linearly independent Ordinary Least-Squares

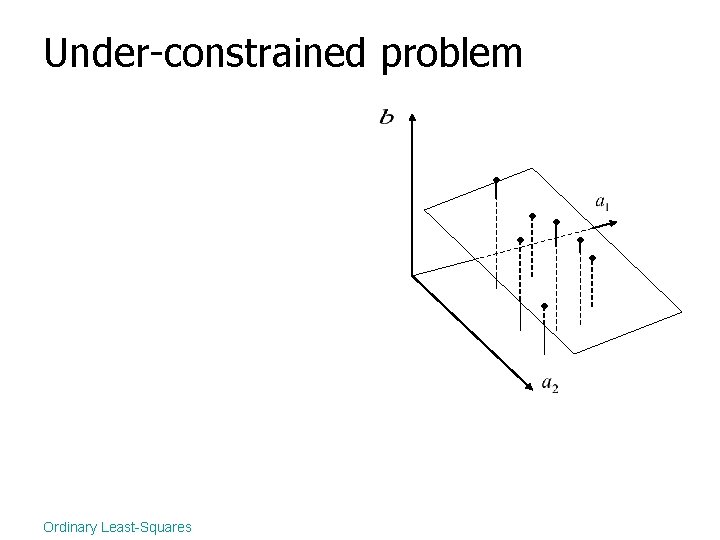
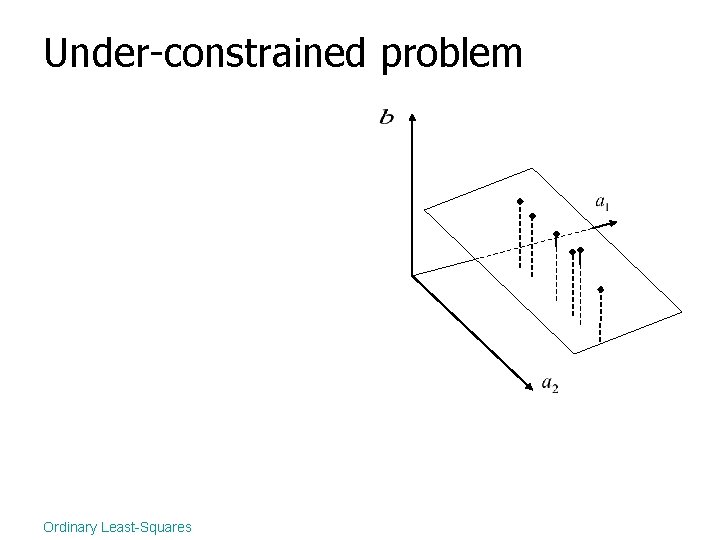
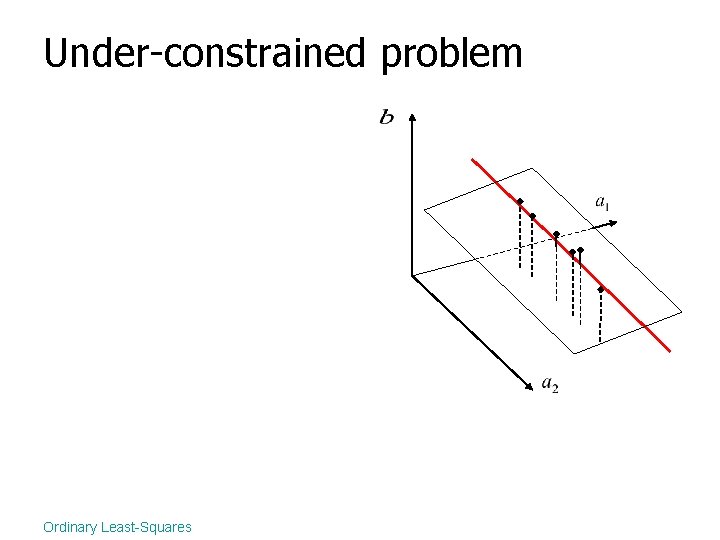
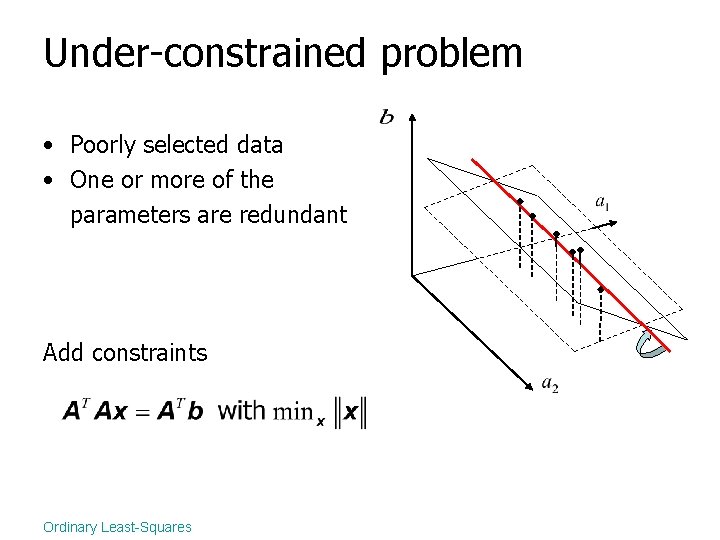
Under-constrained problem Ordinary Least-Squares

Under-constrained problem Ordinary Least-Squares

Under-constrained problem Ordinary Least-Squares

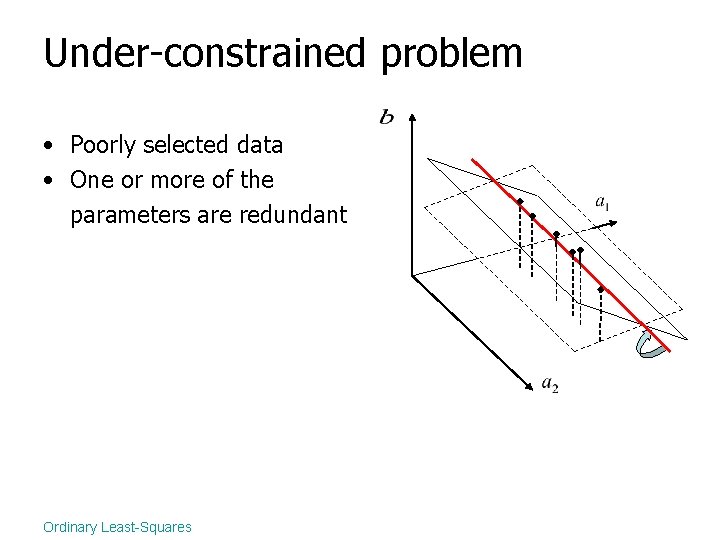
Under-constrained problem • Poorly selected data • One or more of the parameters are redundant Ordinary Least-Squares

Under-constrained problem • Poorly selected data • One or more of the parameters are redundant Add constraints Ordinary Least-Squares

How good is the least-squares criteria? • Optimality: the Gauss-Markov theorem Ordinary Least-Squares

How good is the least-squares criteria? • Optimality: the Gauss-Markov theorem Let and be two sets of random variables and define: Ordinary Least-Squares

How good is the least-squares criteria? • Optimality: the Gauss-Markov theorem Let and be two sets of random variables and define: If Ordinary Least-Squares

How good is the least-squares criteria? • Optimality: the Gauss-Markov theorem Let and be two sets of random variables and define: If Then is the best unbiased linear estimator Ordinary Least-Squares

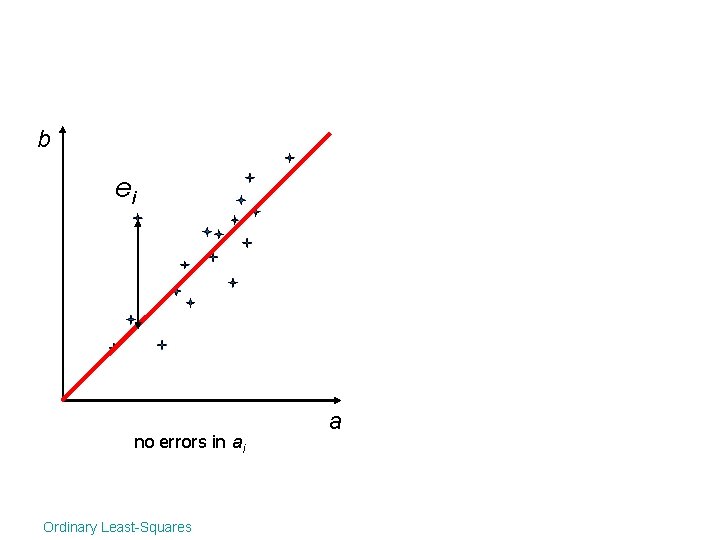
b ei no errors in ai Ordinary Least-Squares a

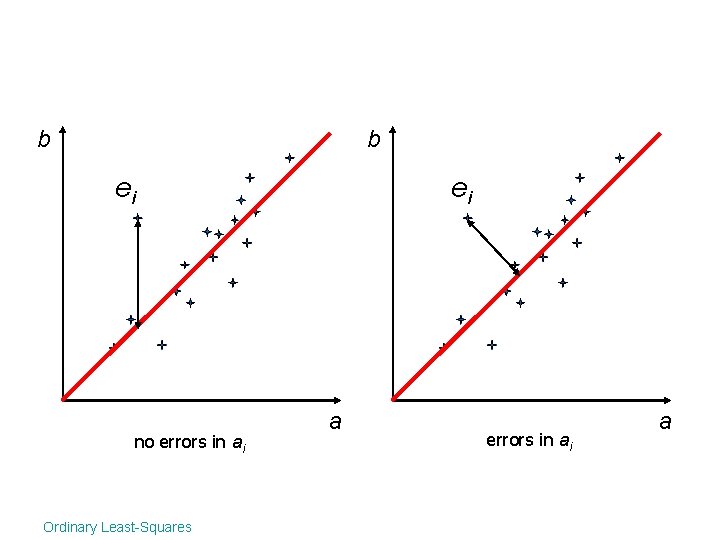
b b ei no errors in ai Ordinary Least-Squares ei a errors in ai a

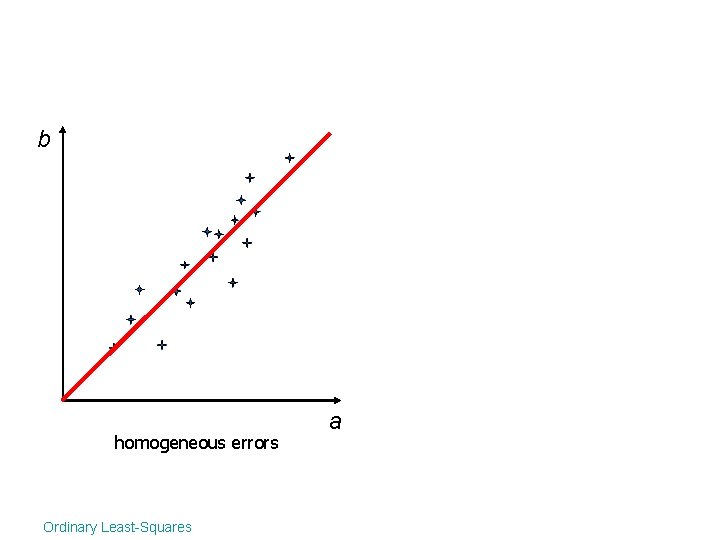
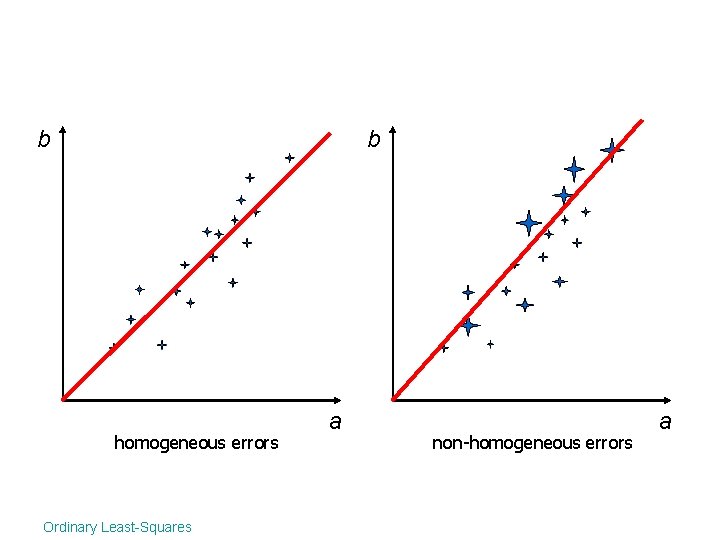
b homogeneous errors Ordinary Least-Squares a

b b homogeneous errors Ordinary Least-Squares a non-homogeneous errors a

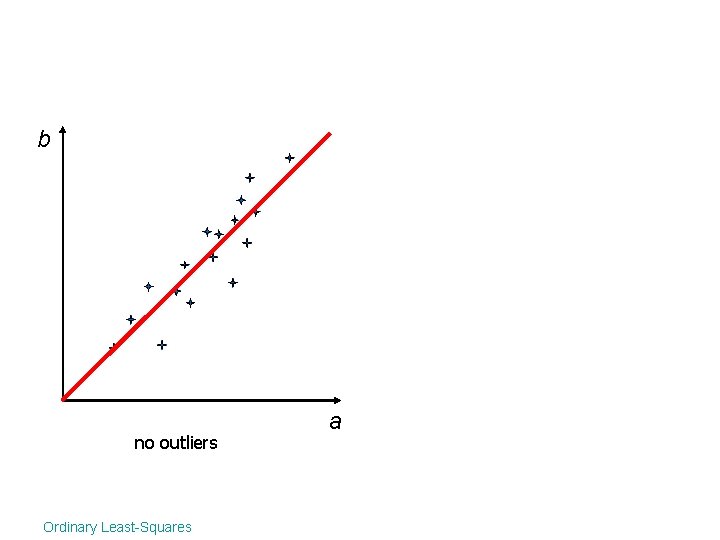
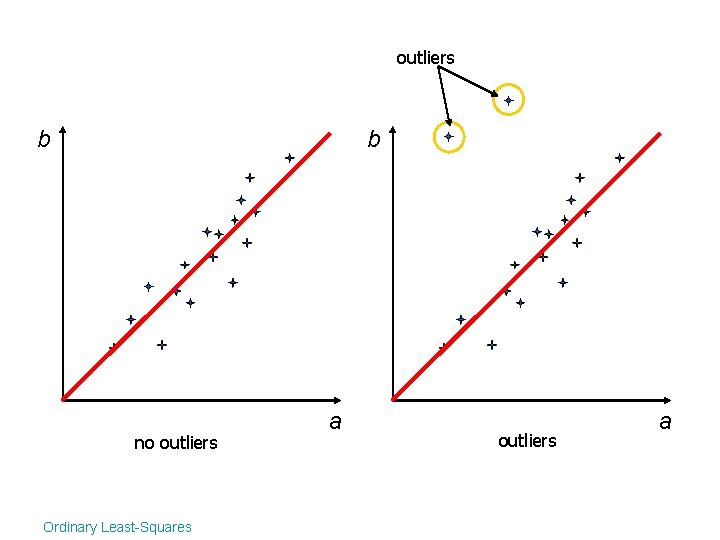
b no outliers Ordinary Least-Squares a

outliers b b no outliers Ordinary Least-Squares a outliers a