Ordering and Carrying Costs Annual Cost The TotalCost

Cost Total Cost Adding Purchasing cost doesn’t change EOQ TC with PD TC without

Quantity Discount By quantity discount, we mean the price per unit decreases as order

Example Demand for a product is 816 units / year ==> D = 816

Total Cost Including Purchasing Cost p 1 p 2 p 3 p 4 0

Total Cost with different Purchase Price Smaller unit prices will raise total cost curve

Quantity Discount Large quantity purchases Price Discount - purchasing cost Fewer orders - Ordering

Total Cost With Price Discount Cost p 1 p 2 0 EOQ p 3

Total Cost Including Purchasing Cost p 1 p 2 p 3 0 EOQ p

Total Cost Including Purchasing Cost The applicable or feasible total cost is initially on

Solution Procedure 1 - Compute EOQ without price considerations. This EOQ is the same

Total Cost Including Purchasing Cost p 1 p 2 p 4 p 3 0

Total Cost Including Purchasing Cost p 1 p 2 0 EOQ p 4 p

Total Cost Including Purchasing Cost p 1 p 3 p 2 0 EOQ Quantity

Example (Q) 1 -49 50 -79 80 -99 100 or more (P) 20 18

Example Is Q = 70 and P = 18 better or Q = 80

Example Demand for a product is 25 tones / day and there are 200

Example Q 600 -. . . 400 -599 0 -399 P 8 9 10

Example Is Q = 490 and P = 9 better or Q = 600

Assignment Ch 12(b) A small manufacturing firm uses approximately 3400 pounds of chemical dye

Cost Ordering, Carrying, and Purchasing Costs Adding Purchasing cost doesn’t change EOQ TC with

Cost Total Cost Including Purchasing Cost p 1 p 2 0 EOQ Quantity

Cost Price Breaks: EOQ Preferred 0 EOQ Quantity

Cost Price Breaks: Discount Point Preferred 0 Q Quantity

The Problem: Part A A small manufacturing firm uses approximately 3400 pounds of chemical

The Problem: Part B A small manufacturing firm uses approximately 3400 pounds of chemical

The Problem: Part B b) If the supplier offered a discount at 1500 pounds

Slides: 36

Download presentation

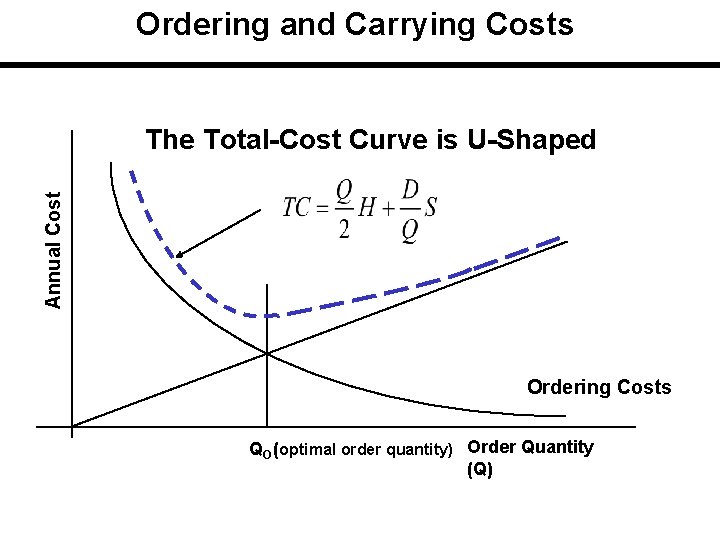
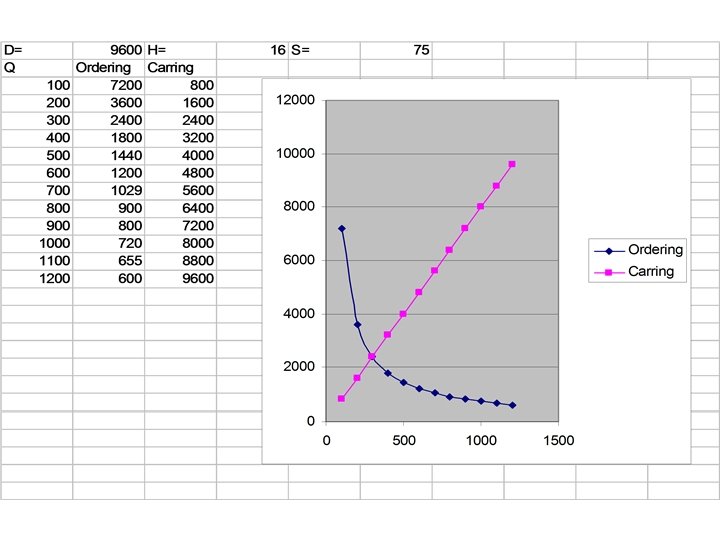
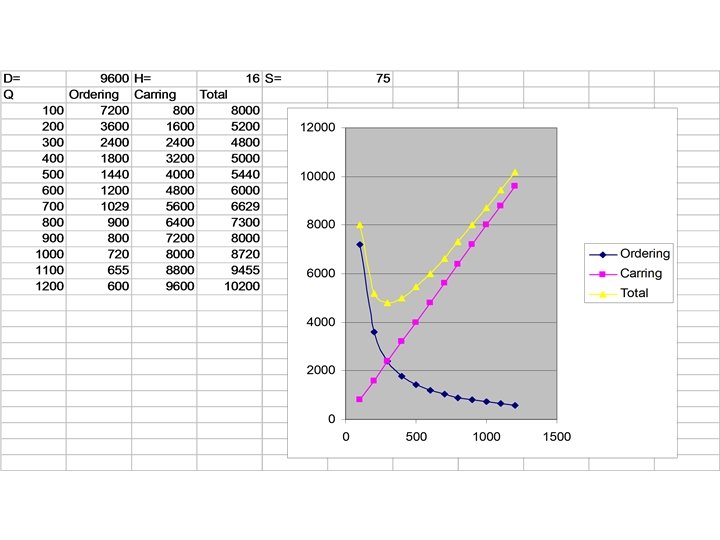
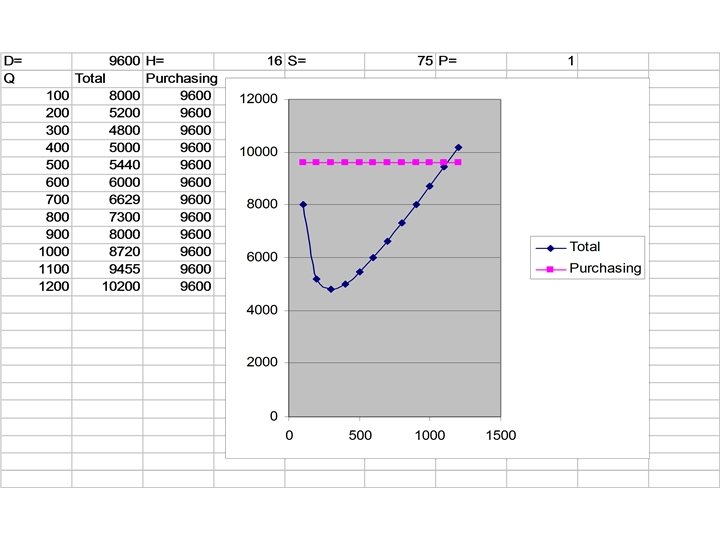
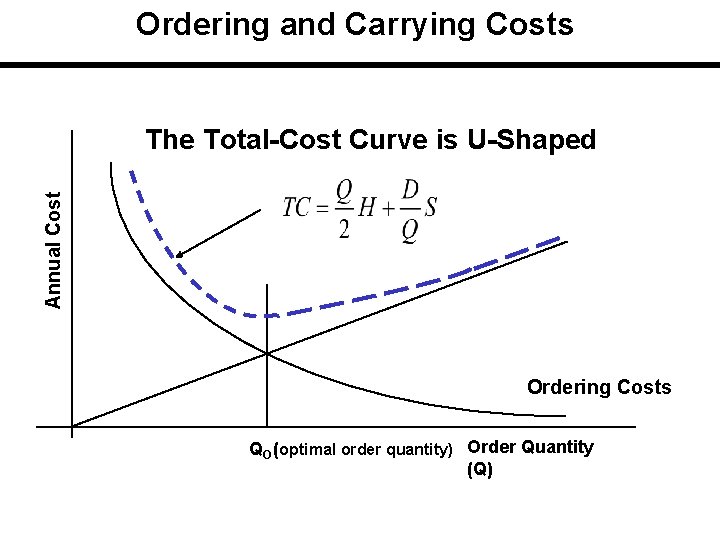
Ordering and Carrying Costs Annual Cost The Total-Cost Curve is U-Shaped Ordering Costs QO (optimal order quantity) Order Quantity (Q)

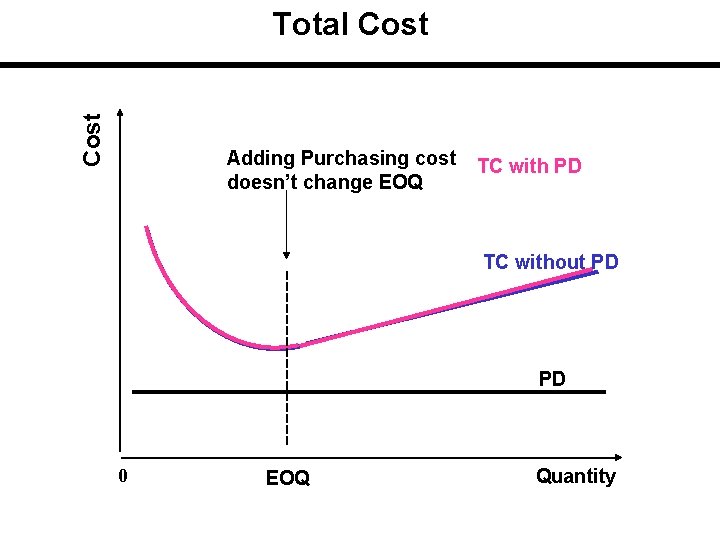
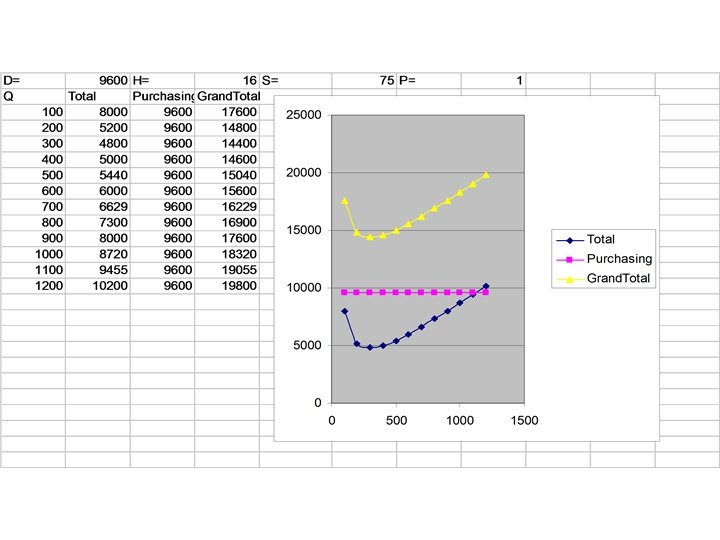
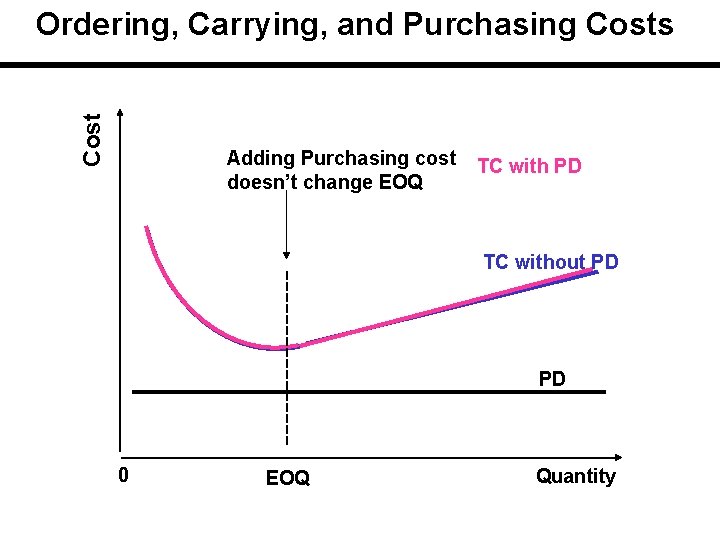
Cost Total Cost Adding Purchasing cost doesn’t change EOQ TC with PD TC without PD PD 0 EOQ Quantity

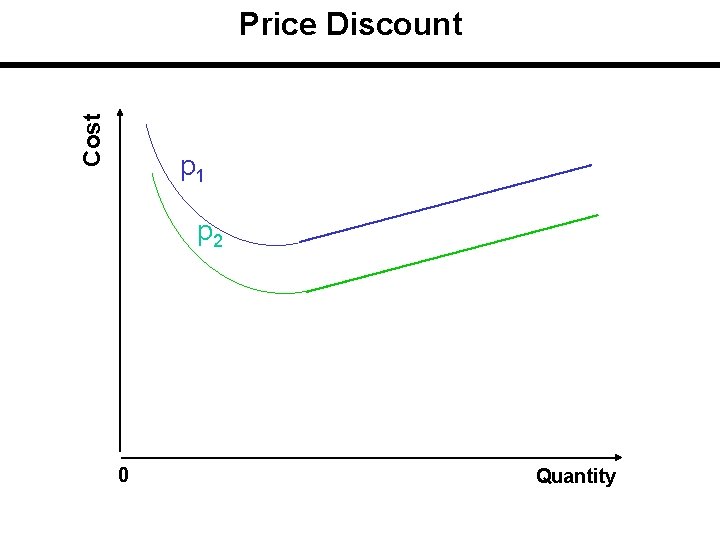
Quantity Discount By quantity discount, we mean the price per unit decreases as order quantity increases. When quantity discounts are offered, there is a separate, U-shaped, total cost curve for each unit price. When unit price decreases, the total cost curve drops. A different total cost curve is applied to each price. If we have quantity discount, then we should weigh the benefit of price discount against the increase in inventory cost.

Example Demand for a product is 816 units / year ==> D = 816 Ordering cost is $12 / order ==> S = 12 Carrying cost is $4 / unit / year ==> H = 4 Price schedule is as follows Quantity (Q) 1 -49 50 -79 80 -99 100 or more Price (P) 20 18 17 16 What is the best quantity that we could order to minimize our total annual cost?

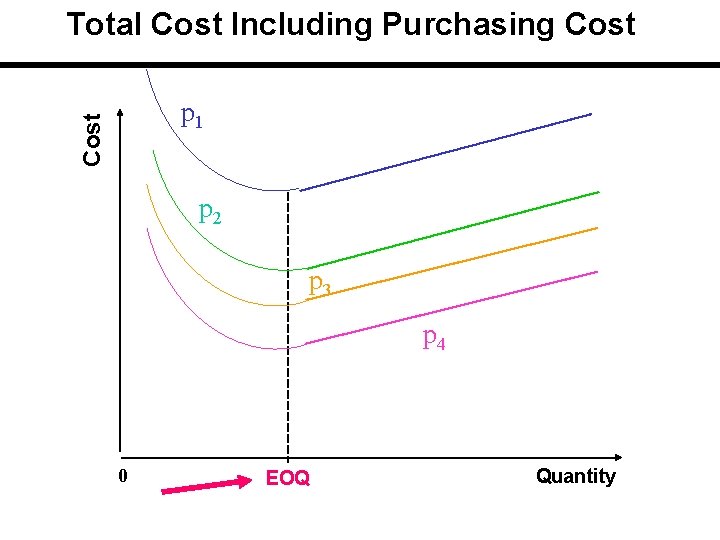
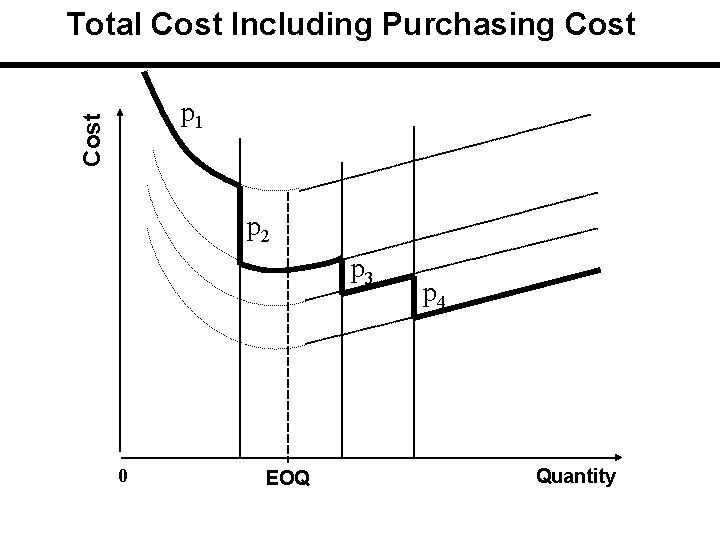
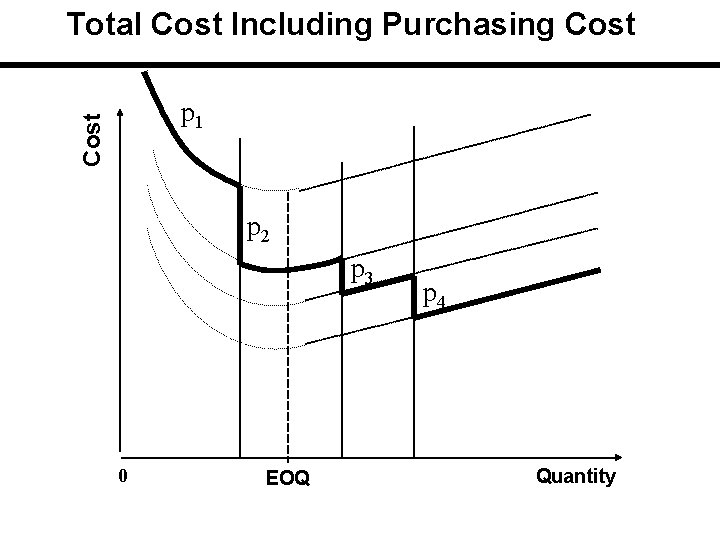
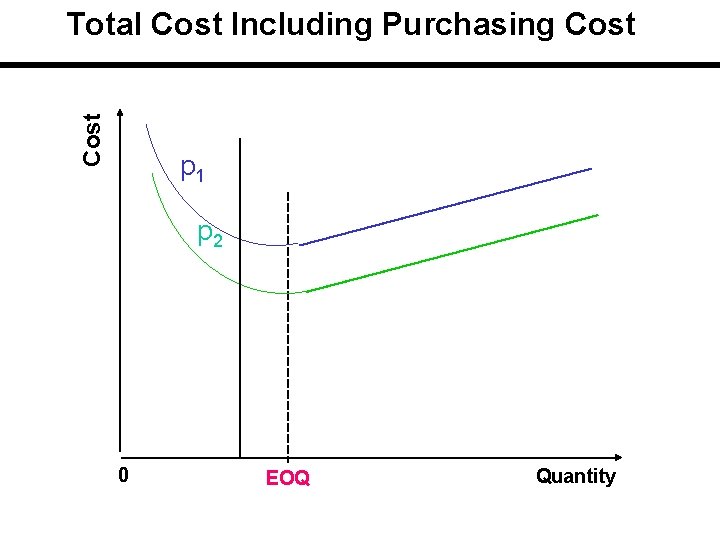
Total Cost Including Purchasing Cost p 1 p 2 p 3 p 4 0 EOQ Quantity

Total Cost with different Purchase Price Smaller unit prices will raise total cost curve less than larger unit prices. For each price, there is a separate U-shaped total cost curve for total cost. Note that no single curve is applied to the entire range of quantities. Each curve is applied to a portion of the range.

Quantity Discount Large quantity purchases Price Discount - purchasing cost Fewer orders - Ordering costs More inventory - inventory cost Our objective is to minimize the total annual costs TC = SD/Q + HQ/2 + PD In our initial model we assumed price is fixed. Therefore we did not include PD in the model.

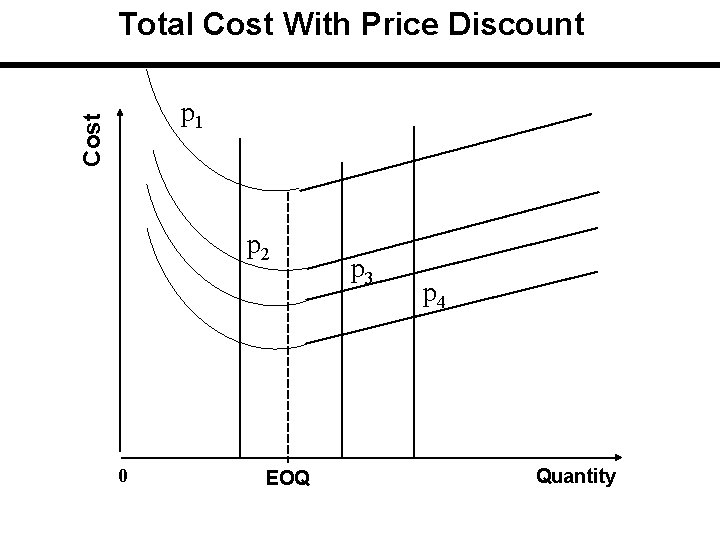
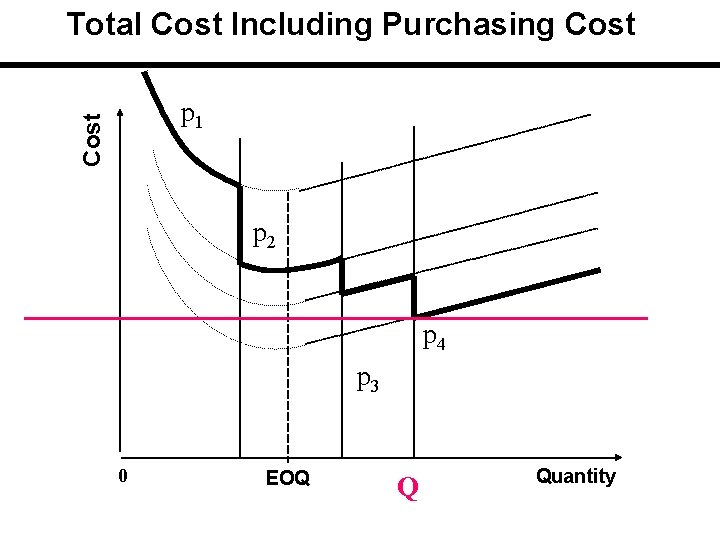
Total Cost With Price Discount Cost p 1 p 2 0 EOQ p 3 p 4 Quantity

Total Cost Including Purchasing Cost p 1 p 2 p 3 0 EOQ p 4 Quantity

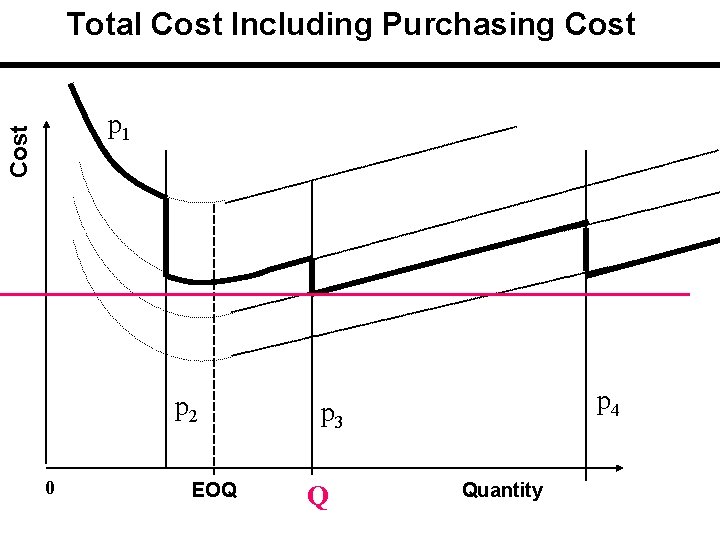
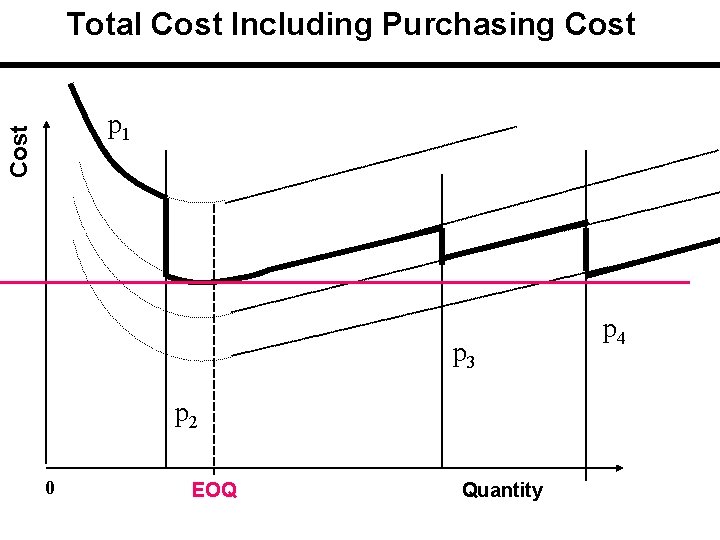
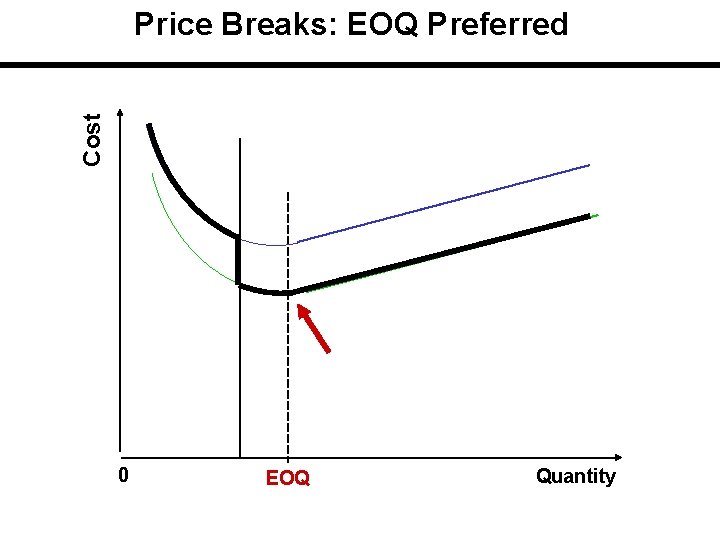
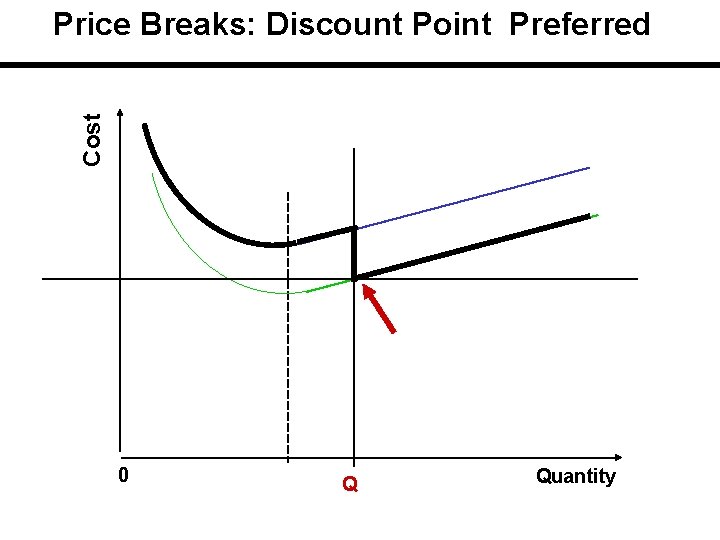
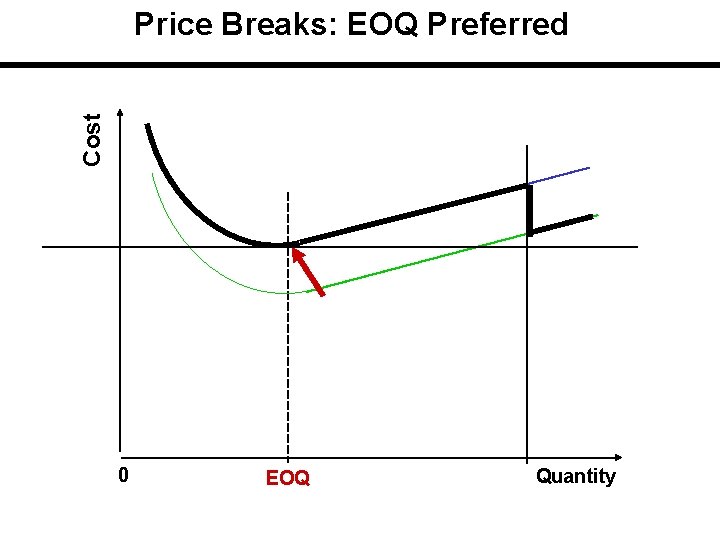
Total Cost Including Purchasing Cost The applicable or feasible total cost is initially on the curve with the highest unit price and then drops down curve by curve at the price breaks. Price breaks are the minimum quantities needed to obtain the discounts. If carrying cost is stated in terms of cost / unit of product / year, there is a single EOQ which is the same for all cost curves.

Solution Procedure 1 - Compute EOQ without price considerations. This EOQ is the same for all prices. 2 - But this EOQ is feasible for only one price. Identify the corresponding price and quantity. 3 -If EOQ is feasible for the lowest price ==>it is the solution. If it is not, then calculate: a) TC for EOQ and corresponding feasible price. Note that TC is… TC = HQ/2 + SD/Q +PD b) calculate TC for all Qs of price break after the above prices. Compare their TC to find the best Q ==>it is the solution.

Total Cost Including Purchasing Cost p 1 p 2 p 4 p 3 0 EOQ Q Quantity

Total Cost Including Purchasing Cost p 1 p 2 0 EOQ p 4 p 3 Q Quantity

Total Cost Including Purchasing Cost p 1 p 3 p 2 0 EOQ Quantity p 4

Example (Q) 1 -49 50 -79 80 -99 100 or more (P) 20 18 17 16 Q=70 is in the 50 -79 range. Therefore, the corresponding price is $18. Obviously, we do not consider P=20, but what about P=17 or P=16?

Total Cost Including Purchasing Cost p 1 p 2 p 3 0 EOQ p 4 Quantity

Example Is Q = 70 and P = 18 better or Q = 80 and P = 17 or Q = 100 and P = 16 TC = HQ/2 + SD/Q + PD TC ( Q = 70 , P = 18) = 4(70)/2 +12(816)/70 + 18(816) TC = 14968 TC ( Q = 80 , P = 17) = 4(80)/2 +12(816)/80 + 17(816) TC = 14154 TC ( Q = 100 , P = 16) = 4(100)/2 +12(816)/100 + 16(816) TC = 13354

Example Demand for a product is 25 tones / day and there are 200 working days / year. ==> D = 25(200) = 5000. Ordering cost is $48 / order ==> S = 48 Carrying cost is $2 / unit / year ==> H = 2 Price schedule is as follows: Quantity (Q) 600 -. . . 400 -599 0 -399 Price (P) 8 9 10 What is the best quantity that we could order to minimize our total annual cost?

Example Q 600 -. . . 400 -599 0 -399 P 8 9 10 Q=490 is in the 400 -599 range. Therefore, the corresponding price is $9. Obviously, we do not consider P=10 but what about P=8?

Example Is Q = 490 and P = 9 better or Q = 600 and P = 8 We should compare their TC TC = HQ/2 + SD/Q + PD TC ( Q = 490 , P = 9) = 2(490)/2 + 48(5000)/490 + 9(5000) TC = 490 + 489. 8 + 45000 = 45979. 8 TC ( Q = 600 , P = 8) = 2(600)/2 + 48(5000)/600 + 8(5000) TC = 41000

Assignment Ch 12(b) A small manufacturing firm uses approximately 3400 pounds of chemical dye per year. Currently the firm purchases 300 pounds per order and pays $3 per pound. The ordering cost is $100 and inventory carrying cost is 51 cents per pound per year. D= 3400, S= 100, H=0. 51 a) The supplier has just announced that orders of 1000 pounds and more will be filled at a price of $2 per pound. Determine the order size that will minimizes the total cost. b) If the supplier offered a discount at 1500 pounds instead of 1000 pounds, what order size will minimize total cost?

Ordering and Carrying Costs Annual Cost The Total-Cost Curve is U-Shaped Ordering Costs QO (optimal order quantity) Order Quantity (Q)

Cost Ordering, Carrying, and Purchasing Costs Adding Purchasing cost doesn’t change EOQ TC with PD TC without PD PD 0 EOQ Quantity

Cost Price Discount p 1 p 2 0 Quantity

Cost Total Cost Including Purchasing Cost p 1 p 2 0 EOQ Quantity

Cost Price Breaks: EOQ Preferred 0 EOQ Quantity

Cost Price Breaks: Discount Point Preferred 0 Q Quantity

Cost Price Breaks: EOQ Preferred 0 EOQ Quantity

The Problem: Part A A small manufacturing firm uses approximately 3400 pounds of chemical dye per year. Currently the firm purchases 300 pounds per order and pays $3 per pound. The ordering cost is $100 and inventory carrying cost is 51 cents per unit per year. D=3400, S= 100, H=. 51 a) The supplier has just announced that orders of 1000 pounds and more will be filled at a price of $2 per pound. DONE Q 0 -999 ≥ 1000 P 3 2

The Problem: Part B A small manufacturing firm uses approximately 3400 pounds of chemical dye per year. Currently the firm purchases 300 pounds per order and pays $3 per pound. The ordering cost is $100 and inventory carrying cost is 51 cents per unit per year. D=3400, S= 100, H=. 51 b) Determine the order size that will minimizes the total cost. If the supplier offered a discount at 1500 pounds instead of 1000 pounds, what order size will minimize total cost? Q 0 -. . . ≥ 1500 P 3 2

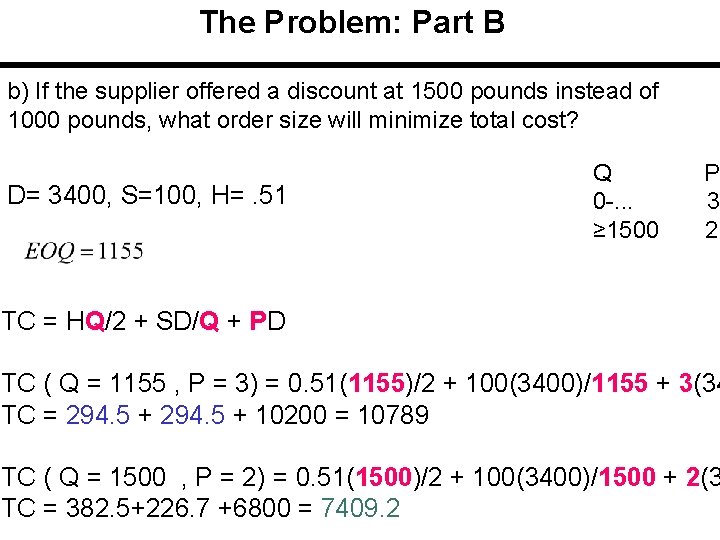
The Problem: Part B b) If the supplier offered a discount at 1500 pounds instead of 1000 pounds, what order size will minimize total cost? D= 3400, S=100, H=. 51 Q 0 -. . . ≥ 1500 P 3 2 TC = HQ/2 + SD/Q + PD TC ( Q = 1155 , P = 3) = 0. 51(1155)/2 + 100(3400)/1155 + 3(34 TC = 294. 5 + 10200 = 10789 TC ( Q = 1500 , P = 2) = 0. 51(1500)/2 + 100(3400)/1500 + 2(3 TC = 382. 5+226. 7 +6800 = 7409. 2