Order StatisticsSelection Problem A more interesting problem is

Order Statistics(Selection Problem) • A more interesting problem is selection: finding the ith smallest element of a set • We will show: – A practical randomized algorithm with O(n) expected running time – A cool algorithm of theoretical interest only with O(n) worst-case running time • Naive algorithm: Sort and index i-th element T(n) = Θ(nlgn)+Θ(1) = Θ(nlgn) • using merge sort or heapsort (not quicksort) Analysis of Algorithms 1

Selection in Expected Linear Time • Randomized algorithm • Divide and conquer • Similar to randomized quicksort – Like quicksort: Partitions input array recursively – Unlike quicksort: – Only works on one side of the partition – Quicksort works on both sides of the partition – Expected running times: – SELECT: E[n] = Θ(n) – QUICKSORT: E[n] = Θ(nlgn) Analysis of Algorithms 2

Selection in Expected Linear Time Analysis of Algorithms 3

Randomized Selection • Key idea: use partition() from quicksort – But, only need to examine one subarray – This savings shows up in running time: O(n) • We will again use a slightly different partition than the book: q = Randomized. Partition(A, p, r) A[q] p A[q] q Analysis of Algorithms r 4

Randomized Selection Randomized. Select(A, p, r, i) if (p == r) then return A[p]; q = Randomized. Partition(A, p, r) k = q - p + 1; if (i == k) then return A[q]; // not in book if (i < k) then return Randomized. Select(A, p, q-1, i); else return Randomized. Select(A, q+1, r, i-k); k A[q] p A[q] q Analysis of Algorithms r 5

Randomized Selection ● Analyzing Randomized. Select() ■ Worst case: partition always 0: n-1 T(n) = T(n-1) + O(n) = O(n 2) (arithmetic series) ○ No better than sorting! ■ “Best” case: suppose a 9: 1 partition T(n) = T(9 n/10) + O(n) = O(n) (Master Theorem, case 3) ○ Better than sorting! Analysis of Algorithms 6

Randomized Selection ● Average case ■ For upper bound, assume ith element always falls in larger side of partition: What happened here? ■ Let’s show that T(n) = O(n) by substitution Analysis of Algorithms 7

Randomized Selection • Assume T(n) cn for sufficiently large c: The recurrence we started with Substitute T(n) cn for T(k) “Split” the recurrence Expand arithmetic series Multiply it out Analysis of Algorithms 8

Randomized Selection • Assume T(n) cn for sufficiently large c: The recurrence so far What happened Multiply it out here? What happened Subtract c/2 here? Rearrange the arithmetic What happened here? What set out to prove Whatwehappened here? Analysis of Algorithms 9

Worst-Case Linear-Time Selection ● Randomized algorithm works well in practice ● What follows is a worst-case linear time algorithm, really of theoretical interest only ● Basic idea: ■ Generate a good partitioning element ■ Call this element x Analysis of Algorithms 10

Selection in Worst Case Linear Time SELECT(S, n, i) // return i-th element in set S with n elements if n≤ 5 then SORT S and return the i-th element DIVIDE S into n/5 groups first n/5 groups are of size 5, last group is of size n mod 5 FIND median set M={m 1 , …, m n/5 } mj = median of j-th group x ← SELECT(M, n/5 /2 +1) PARTITION set S around the pivot x into L and R if i ≤ |L| then return SELECT(L, |L| , i) else return SELECT(R, n–|L| , i–|L|) Analysis of Algorithms 11

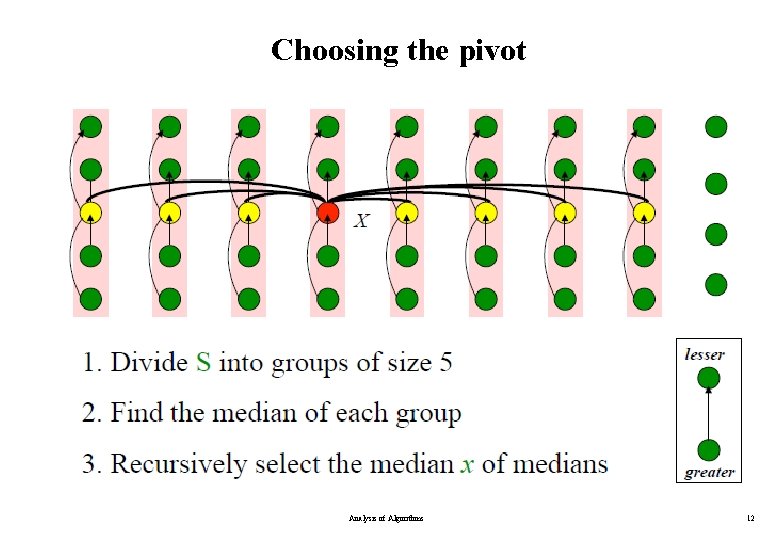
Choosing the pivot Analysis of Algorithms 12

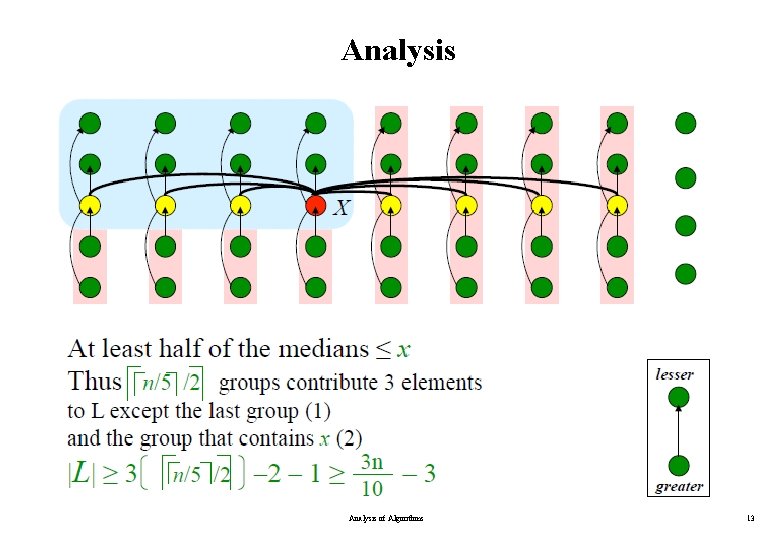
Analysis of Algorithms 13

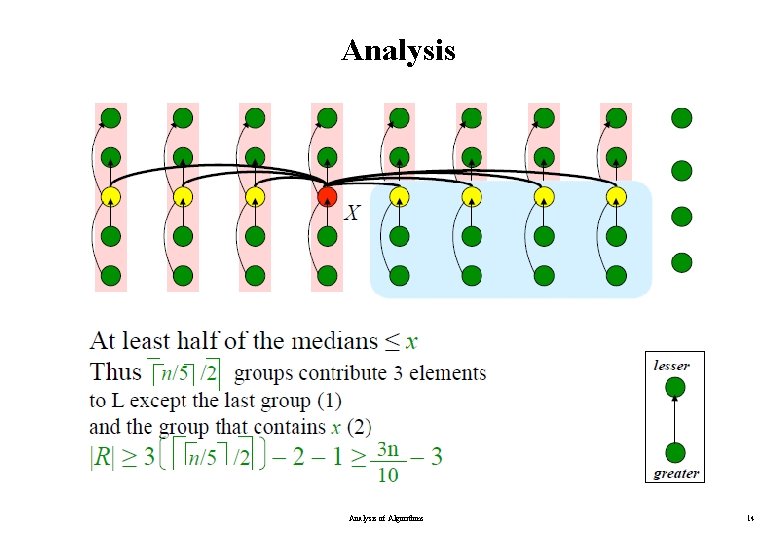
Analysis of Algorithms 14

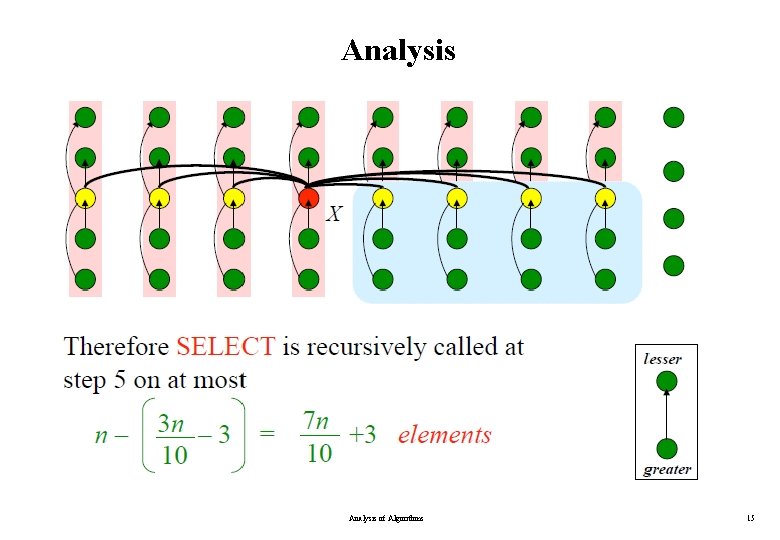
Analysis of Algorithms 15

Selection in Worst Case Linear Time SELECT(S, n, i) // return i-th element in set S with n elements if n≤ 5 then SORT S and return the i-th element DIVIDE S into n/5 groups first n/5 groups are of size 5, last group is of size n mod 5 FIND median set M={m 1 , …, m n/5 } mj = median of j-th group x ← SELECT(M, n/5 /2 +1) PARTITION set S around the pivot x into L and R if i ≤ |L| then return SELECT(L, |L| , i) else return SELECT(R, n–|L| , i–|L|) Analysis of Algorithms 16

Selection in Worst Case Linear Time Analysis of Algorithms 17