Orbital Mechanics Keplers Third Law P 2 a

Orbital Mechanics:

Kepler’s Third Law: P 2 = a 3 x M-1 • Where M = Mass of the System in SOLAR MASSES • Where a = Semi-Major Axis of Orbit in AU • Where P = Orbital Period in YEARS • This law is General, which means that it works for ANY orbiting body (that is much smaller than the object it orbits).

What’s a Moon Good For? • This new equation means that we can find out exactly how big all the planets are relative to the Sun! • How? Using their moons! • Galileo had discovered that some planets had moons that appeared to orbit them, just like our moon. B = A x TAN(C) B = planet-moon dist. (AU) • Thus, we could use the period of these orbits to get the masses of the planets! C = angle on sky A = sun-Earth dist. (AU)

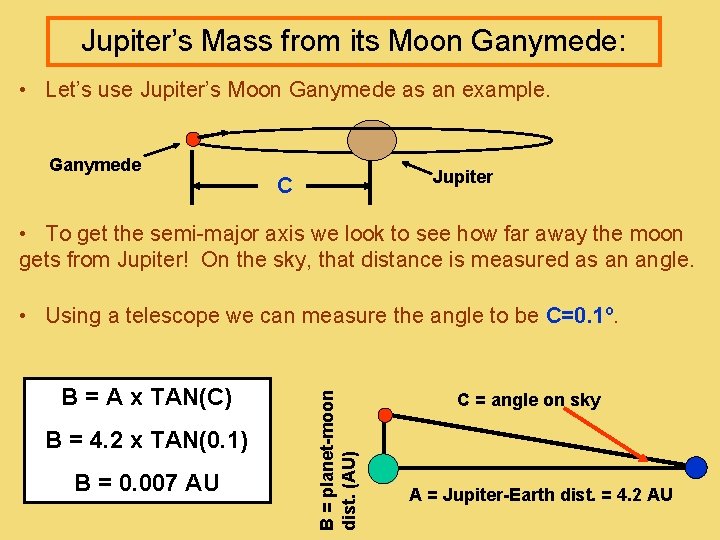
Jupiter’s Mass from its Moon Ganymede: • Let’s use Jupiter’s Moon Ganymede as an example. Ganymede Jupiter C • To get the semi-major axis we look to see how far away the moon gets from Jupiter! On the sky, that distance is measured as an angle. B = A x TAN(C) B = 4. 2 x TAN(0. 1) B = 0. 007 AU B = planet-moon dist. (AU) • Using a telescope we can measure the angle to be C=0. 1º. C = angle on sky A = Jupiter-Earth dist. = 4. 2 AU

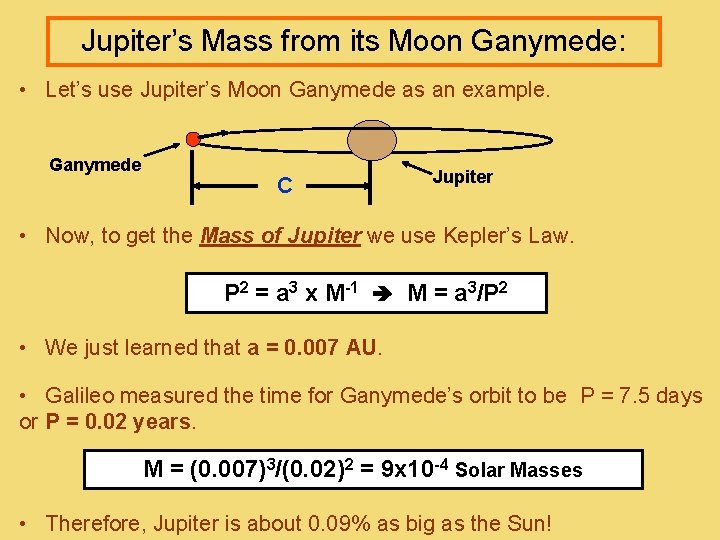
Jupiter’s Mass from its Moon Ganymede: • Let’s use Jupiter’s Moon Ganymede as an example. Ganymede C Jupiter • Now, to get the Mass of Jupiter we use Kepler’s Law. P 2 = a 3 x M-1 M = a 3/P 2 • We just learned that a = 0. 007 AU. • Galileo measured the time for Ganymede’s orbit to be P = 7. 5 days or P = 0. 02 years. M = (0. 007)3/(0. 02)2 = 9 x 10 -4 Solar Masses • Therefore, Jupiter is about 0. 09% as big as the Sun!

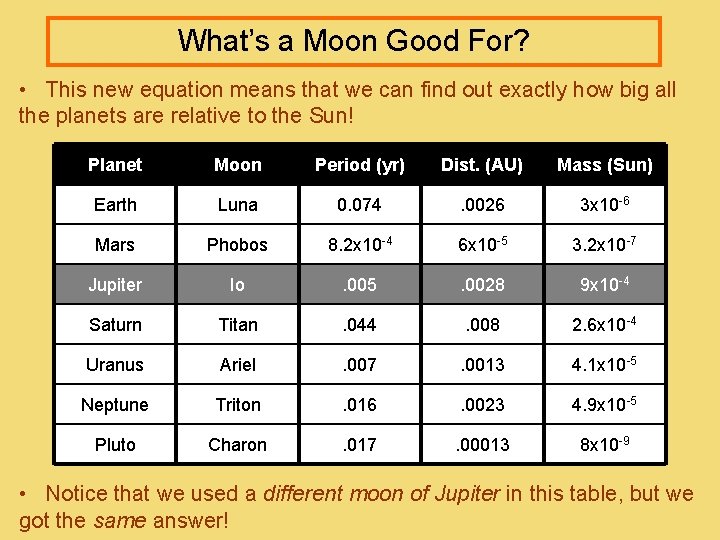
What’s a Moon Good For? • This new equation means that we can find out exactly how big all the planets are relative to the Sun! Planet Moon Period (yr) Dist. (AU) Mass (Sun) Earth Luna 0. 074 . 0026 3 x 10 -6 Mars Phobos 8. 2 x 10 -4 6 x 10 -5 3. 2 x 10 -7 Jupiter Io . 005 . 0028 9 x 10 -4 Saturn Titan . 044 . 008 2. 6 x 10 -4 Uranus Ariel . 007 . 0013 4. 1 x 10 -5 Neptune Triton . 016 . 0023 4. 9 x 10 -5 Pluto Charon . 017 . 00013 8 x 10 -9 • Notice that we used a different moon of Jupiter in this table, but we got the same answer!

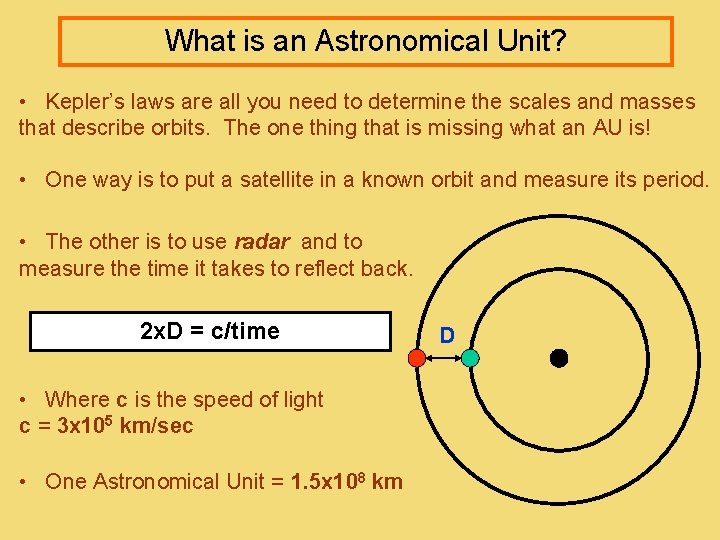
What is an Astronomical Unit? • Kepler’s laws are all you need to determine the scales and masses that describe orbits. The one thing that is missing what an AU is! • One way is to put a satellite in a known orbit and measure its period. • The other is to use radar and to measure the time it takes to reflect back. 2 x. D = c/time • Where c is the speed of light c = 3 x 105 km/sec • One Astronomical Unit = 1. 5 x 108 km D

Kepler’s Third Law (Revised Edition) • With a direct measurement of what an AU is, we can develop a more comprehensive form for Kepler’s Law (with gravity) • Where G=Gravitational Constant G=6. 7 x 10 -11 (M in kg, P in sec, and a in m). • In the above equation M = M 1+M 2, the total mass of the orbiting system • Most of the time the mass of the orbiting body is small enough that we can ignore it. a

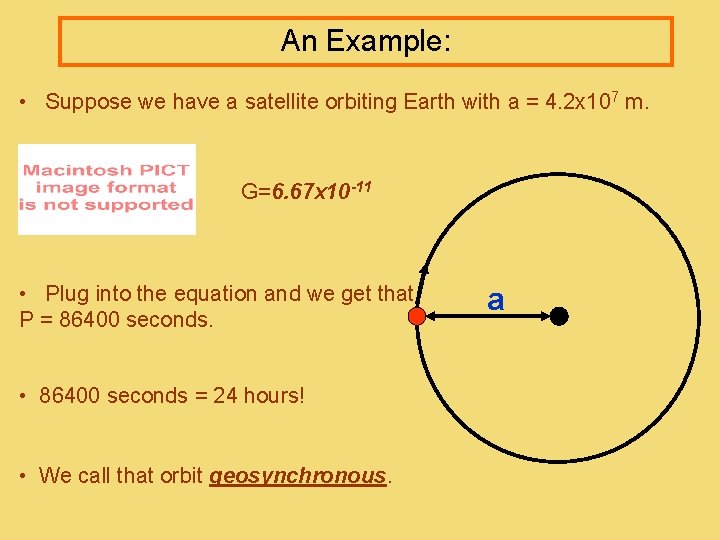
An Example: • Suppose we have a satellite orbiting Earth with a = 4. 2 x 107 m. G=6. 67 x 10 -11 • Plug into the equation and we get that P = 86400 seconds. • 86400 seconds = 24 hours! • We call that orbit geosynchronous. a

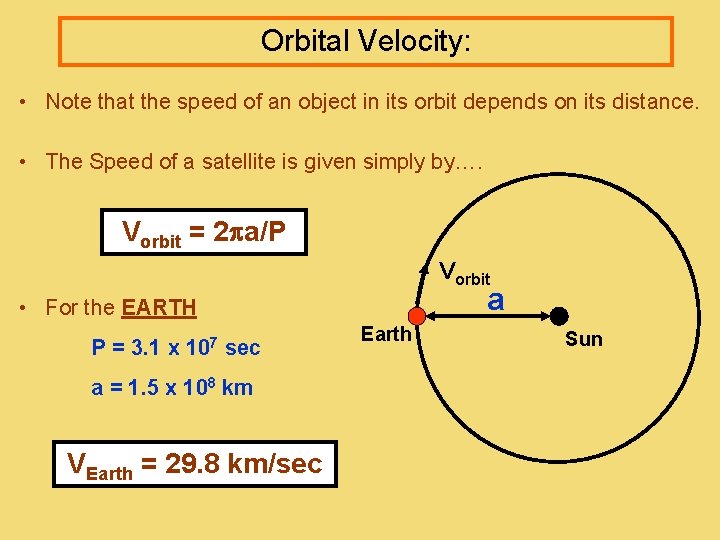
Orbital Velocity: • Note that the speed of an object in its orbit depends on its distance. • The Speed of a satellite is given simply by…. Vorbit = 2 a/P Vorbit a • For the EARTH P = 3. 1 x 107 sec a = 1. 5 x 108 km VEarth = 29. 8 km/sec Earth Sun

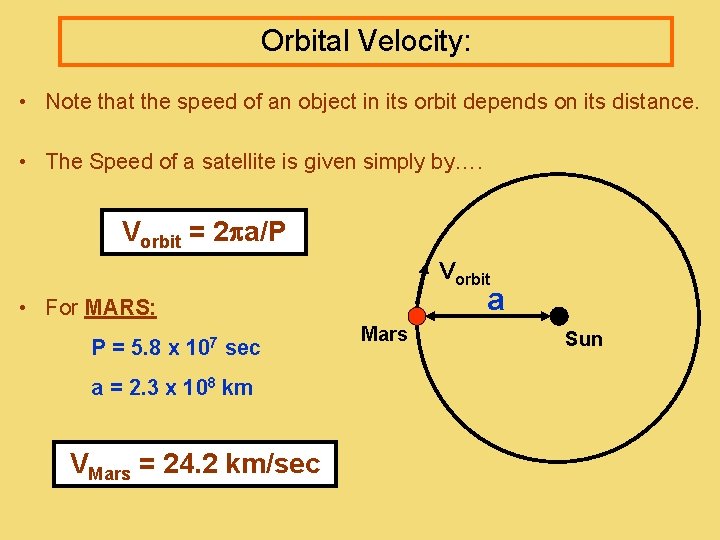
Orbital Velocity: • Note that the speed of an object in its orbit depends on its distance. • The Speed of a satellite is given simply by…. Vorbit = 2 a/P Vorbit a • For MARS: P = 5. 8 x 107 sec a = 2. 3 x 108 km VMars = 24. 2 km/sec Mars Sun

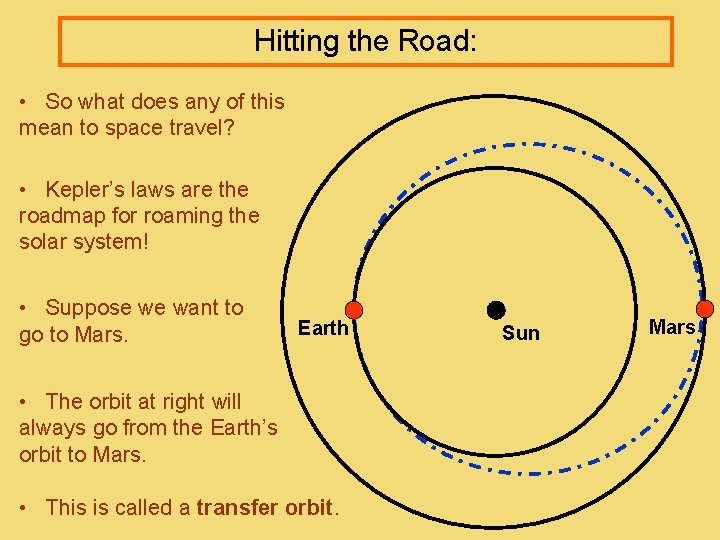
Hitting the Road: • So what does any of this mean to space travel? • Kepler’s laws are the roadmap for roaming the solar system! • Suppose we want to go to Mars. Earth • The orbit at right will always go from the Earth’s orbit to Mars. • This is called a transfer orbit. Sun Mars

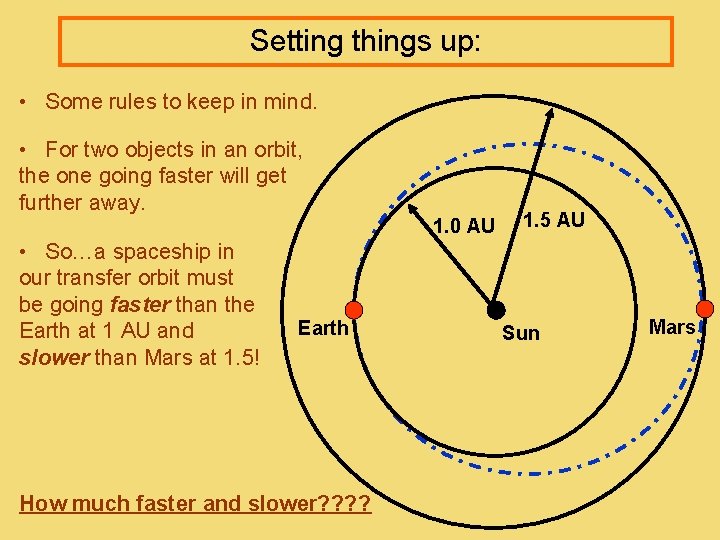
Setting things up: • Some rules to keep in mind. • For two objects in an orbit, the one going faster will get further away. 1. 0 AU • So…a spaceship in our transfer orbit must be going faster than the Earth at 1 AU and slower than Mars at 1. 5! Earth How much faster and slower? ? 1. 5 AU Sun Mars

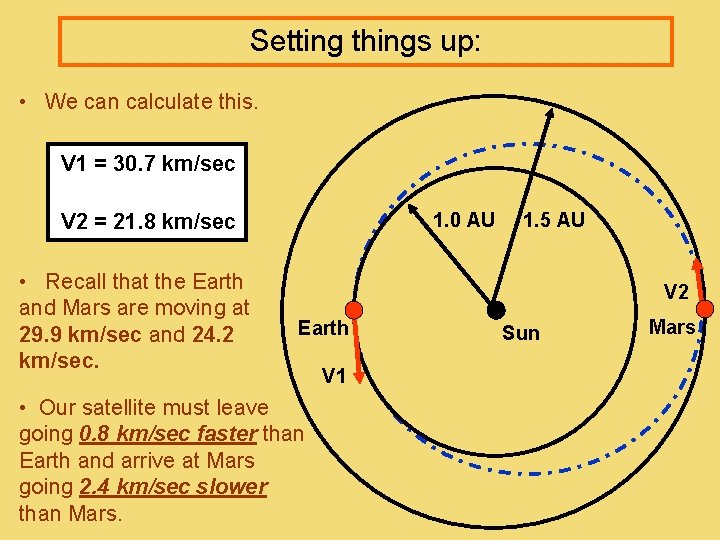
Setting things up: • We can calculate this. V 1 = 30. 7 km/sec 1. 0 AU V 2 = 21. 8 km/sec • Recall that the Earth and Mars are moving at 29. 9 km/sec and 24. 2 km/sec. 1. 5 AU V 2 Earth • Our satellite must leave going 0. 8 km/sec faster than Earth and arrive at Mars going 2. 4 km/sec slower than Mars. V 1 Sun Mars

Escape Velocity: • It’s not enough to give a spacecraft 0. 8 km seconds, we must also get it off of the Earth. • To leave a planet requires overcoming gravity, which acts like an elastic band attached to our spacecraft. We have to snap it. • To escape, our spacecraft must have energy of motion equal (or greater than) the gravitational energy holding it down. spacecraft mass 1/2 MV 2 = g. Mr starting altitude acceleration of gravity V 2 = 2 g. R • This reduces to and 5. 2 km/sec for Mars. which is 11. 8 km/sec for Earth

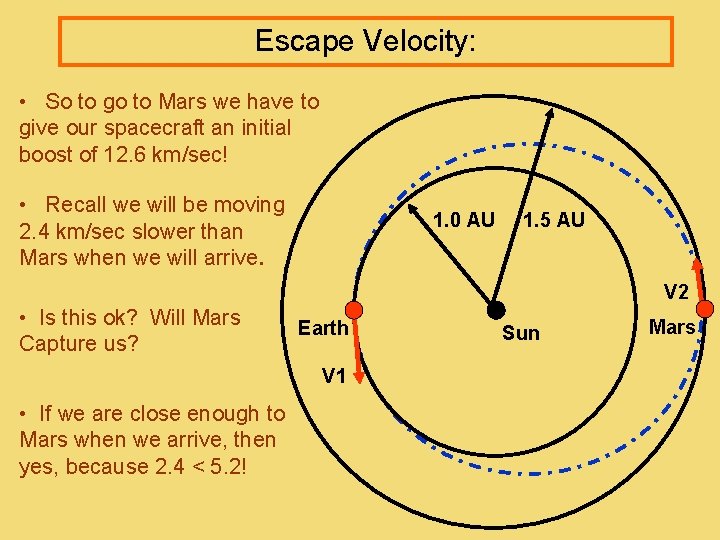
Escape Velocity: • So to go to Mars we have to give our spacecraft an initial boost of 12. 6 km/sec! • Recall we will be moving 2. 4 km/sec slower than Mars when we will arrive. 1. 0 AU 1. 5 AU V 2 • Is this ok? Will Mars Capture us? Earth V 1 • If we are close enough to Mars when we arrive, then yes, because 2. 4 < 5. 2! Sun Mars

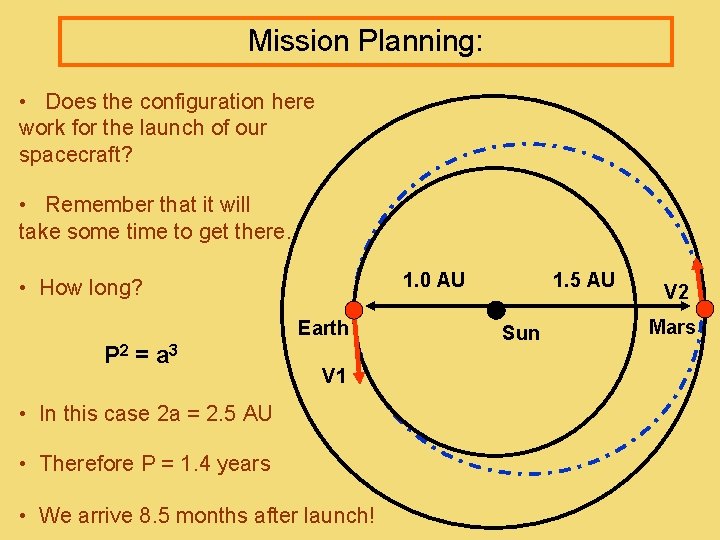
Mission Planning: • Does the configuration here work for the launch of our spacecraft? • Remember that it will take some time to get there. 1. 0 AU • How long? Earth P 2 = a 3 V 1 • In this case 2 a = 2. 5 AU • Therefore P = 1. 4 years • We arrive 8. 5 months after launch! 1. 5 AU Sun V 2 Mars

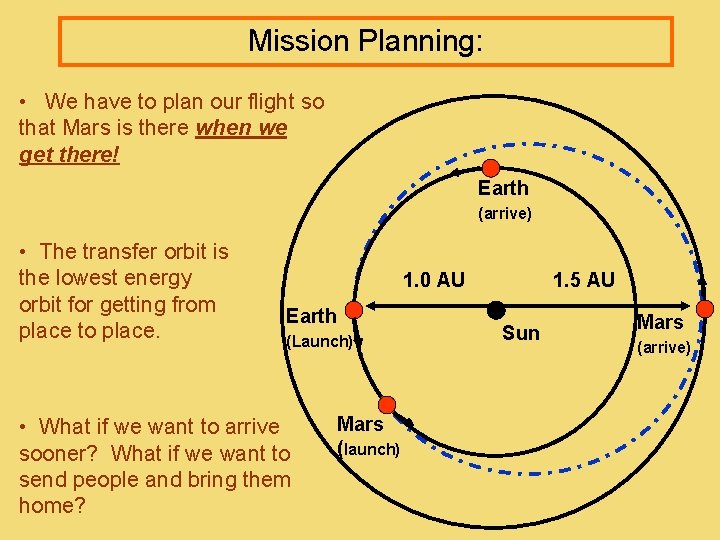
Mission Planning: • We have to plan our flight so that Mars is there when we get there! Earth (arrive) • The transfer orbit is the lowest energy orbit for getting from place to place. 1. 0 AU Earth (Launch) • What if we want to arrive sooner? What if we want to send people and bring them home? Mars (launch) 1. 5 AU Sun Mars (arrive)

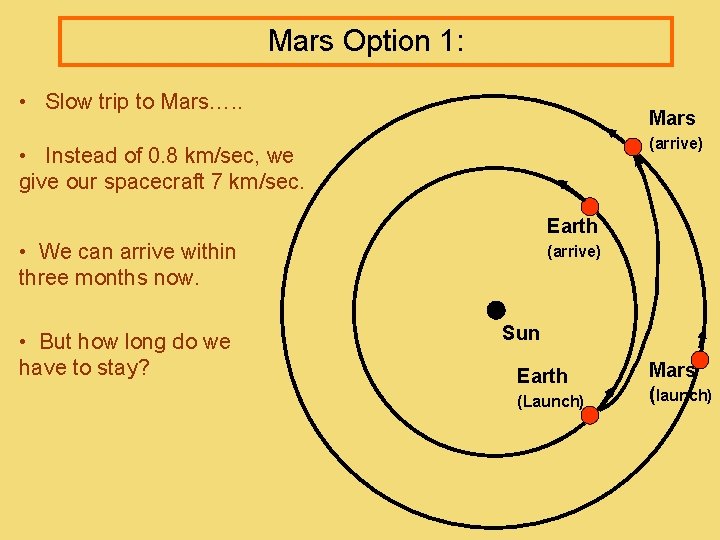
Mars Option 1: • Slow trip to Mars…. . Mars (arrive) • Instead of 0. 8 km/sec, we give our spacecraft 7 km/sec. Earth • We can arrive within three months now. • But how long do we have to stay? (arrive) Sun Earth (Launch) Mars (launch)

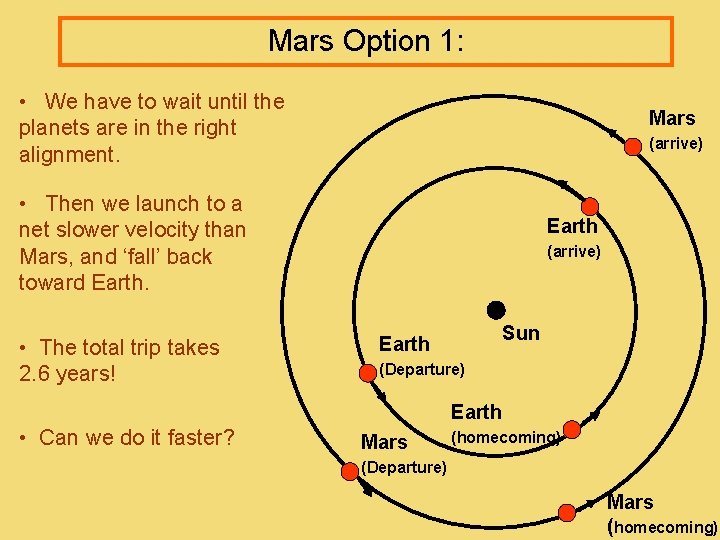
Mars Option 1: • We have to wait until the planets are in the right alignment. Mars (arrive) • Then we launch to a net slower velocity than Mars, and ‘fall’ back toward Earth. • The total trip takes 2. 6 years! Earth (arrive) Sun Earth (Departure) Earth • Can we do it faster? Mars (homecoming) (Departure) Mars (homecoming)

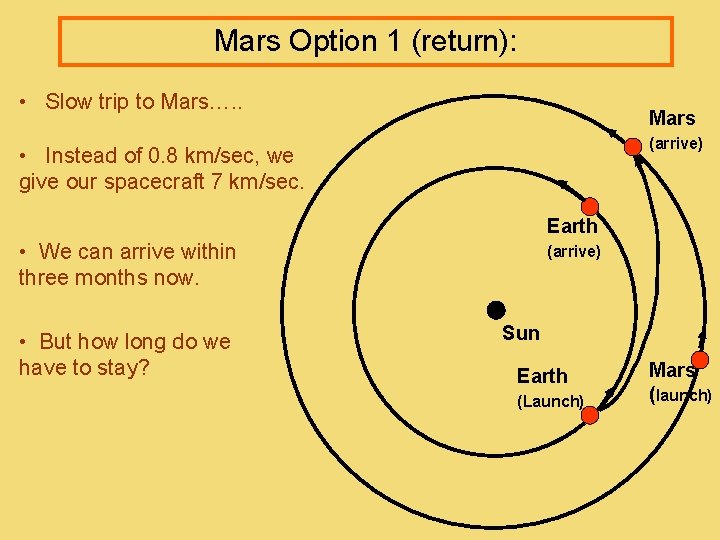
Mars Option 1 (return): • Slow trip to Mars…. . Mars (arrive) • Instead of 0. 8 km/sec, we give our spacecraft 7 km/sec. Earth • We can arrive within three months now. • But how long do we have to stay? (arrive) Sun Earth (Launch) Mars (launch)

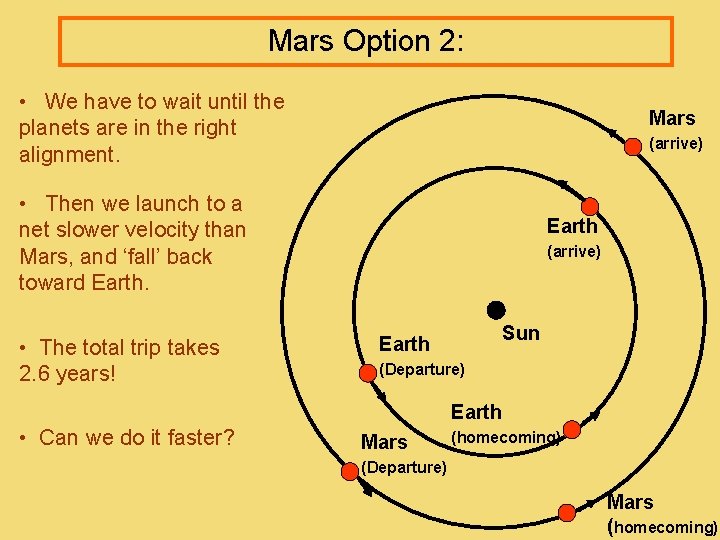
Mars Option 2: • We have to wait until the planets are in the right alignment. Mars (arrive) • Then we launch to a net slower velocity than Mars, and ‘fall’ back toward Earth. • The total trip takes 2. 6 years! Earth (arrive) Sun Earth (Departure) Earth • Can we do it faster? Mars (homecoming) (Departure) Mars (homecoming)

Pluto Neptune Uranus Saturn Jupiter Mars Earth Venus Mercury