ORBITAL DECAY OF HIGH VELOCITY CLOUDS LUMA FOHTUNG

ORBITAL DECAY OF HIGH VELOCITY CLOUDS LUMA FOHTUNG UW-Madison Astrophysics REU 2004 What is the fate of the gas clouds orbiting the Milky. Way Galaxy?

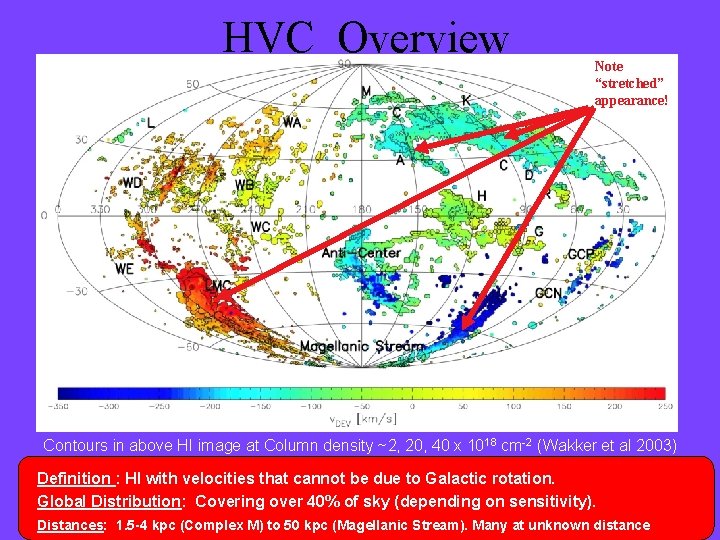
HVC Overview Note “stretched” appearance! Contours in above HI image at Column density ~2, 20, 40 x 1018 cm-2 (Wakker et al 2003) Definition : HI with velocities that cannot be due to Galactic rotation. Global Distribution: Covering over 40% of sky (depending on sensitivity). Distances: 1. 5 -4 kpc (Complex M) to 50 kpc (Magellanic Stream). Many at unknown distance

High Velocity Cloud “Streams” What determines the orbit of a HVC? • Gravity and random motions only? • Drag forces due to gaseous halo and disk of Galaxy 50 kpc Schematic diagram of Magellanic Stream ? How long does it take a HVC to merge with the Galaxy? What happens during the process?

My Project Goal: Develop numerical models of orbital motion for high velocity clouds Tools: Fortran code (for the models) and IDL (to view the output) Method: Write programs, generate the output, use plots to check our results, and debugging… Lots of debugging…

Initial Conditions for Program • Calculate the orbit of a “test cloud” of 10, 000 points. • Specify average position and velocity of test cloud. (x, y, z)average (vx, vy, vz)average • Specify Gaussian scale length for cloud: s. R • Specify Gaussian velocity dispersion for cloud: sv • Set up information on desired time step and stopping time. • Choose model for gravitational field of Galaxy (Dehnen & Binney 1998 “Mass Models of the Milky Way”)

Numerical Methods Random number generator: Needed to set up randomized position and velocity for test clouds. Differential equation solver: Needed to evolve equations of motion for test clouds. I used a Runge-Kutta method (Numerical Recipes). Equations of motion: Set of six coupled differential equations.

An example run Before After

Checking the calculations 1. I checked our differential equation solver with simple (not coupled) equations with known solution. 2. 2. I used the Runge-Kutta method and gravitational field of a point source to calculate the orbit of the Sun. 3. Using a Galactic mass model, we calculated orbit for the current position and velocity of the Sun. 4. Checked total energy and orbital angular momentum. Both were conserved to within 0. 01%.

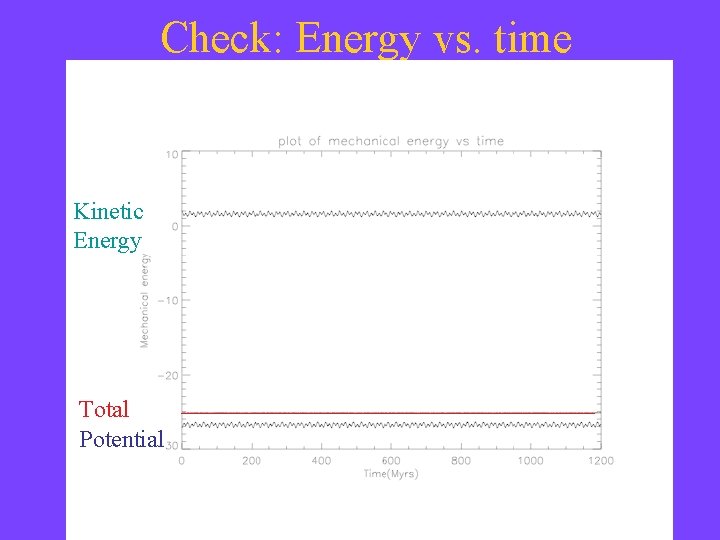
Check: Energy vs. time Kinetic Energy Total Potential

So far… • Development of the FORTRAN code to calculate orbits for clouds. • Development of IDL routines to visualize output. • Initializing using solar type orbits. • Trace of resulting cloud and stretching of initial cloud.

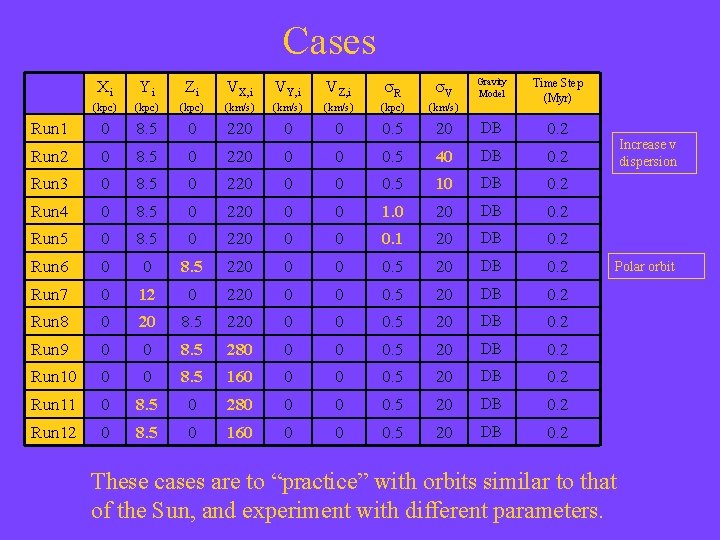
Cases Xi Yi Zi VX, i VY, i VZ, i s. R s. V (kpc) (km/s) (kpc) (km/s) Run 1 0 8. 5 0 220 0 0 0. 5 Run 2 0 8. 5 0 220 0 0 Run 3 0 8. 5 0 220 0 Run 4 0 8. 5 0 220 Run 5 0 8. 5 0 Run 6 0 0 Run 7 0 Run 8 Gravity Model Time Step (Myr) 20 DB 0. 2 0. 5 40 DB 0. 2 0 0. 5 10 DB 0. 2 0 0 1. 0 20 DB 0. 2 220 0 0 0. 1 20 DB 0. 2 8. 5 220 0 0 0. 5 20 DB 0. 2 12 0 220 0 0 0. 5 20 DB 0. 2 0 20 8. 5 220 0 0 0. 5 20 DB 0. 2 Run 9 0 0 8. 5 280 0 0 0. 5 20 DB 0. 2 Run 10 0 0 8. 5 160 0 0 0. 5 20 DB 0. 2 Run 11 0 8. 5 0 280 0 0 0. 5 20 DB 0. 2 Run 12 0 8. 5 0 160 0 0 0. 5 20 DB 0. 2 Increase v dispersion Polar orbit These cases are to “practice” with orbits similar to that of the Sun, and experiment with different parameters.

Comparison of Cases Run 1: Standard Case

Effect of Increasing sv Run 2: Double velocity dispersion to 40 km/s

Polar orbit Run 6: Orbit in XZ plane

What I have learnt…. -A LOT of programming (IDL and Fortran) -a better insight about astronomy A WHOLE LOT OF PATIENCE

Future work Study the orbits of clouds much further away from the Galaxy, objects similar to the Magellanic Stream. Add and test the effects of gaseous drag on our test particles. Experiment with different density distributions and include the effect of possible outflows from the center of the Galaxy. Check on the importance of self-gravity for the cloud. Consider how magnetic effects would alter drag on clouds.

Acknowledgements • My advisor: Dr Bob Benjamin • UW Madison REU program • NASA

Any Questions?