Options Pricing by Arbitrage 1 Example What is

Options: Pricing by Arbitrage 1
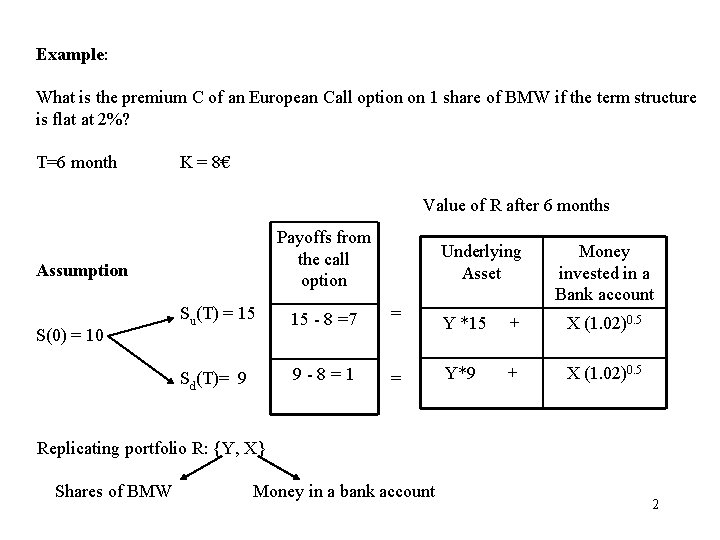
Example: What is the premium C of an European Call option on 1 share of BMW if the term structure is flat at 2%? T=6 month K = 8€ Value of R after 6 months Payoffs from the call option Underlying Asset Su(T) = 15 = 15 - 8 =7 Money invested in a Bank account Y *15 + X (1. 02)0. 5 9 - 8 = 1 Sd(T)= 9 = Y*9 + X (1. 02)0. 5 Assumption S(0) = 10 Replicating portfolio R: {Y, X} Shares of BMW Money in a bank account 2

The composition of the replicating portfolio is given by the solution of the system 7 = Y 15 + X(1. 02)0. 5 thus, Y = 1 share of BMW and X = -€ 7. 92 1 = Y 9 + X(1. 02) 0. 5 The call option can be replicated with a portfolio R composed of 1 share of BMW and borrowing for € 7. 92 At T = 6 month the value of this portfolio will be exactly equal to € 7 € 1 if S(T) = 15 and if S(T) = 9 Conclusion: The no arbitrage price for the call is C = Y* S(0) + X = 1 * 10 – 7. 92 = € 2. 08 3
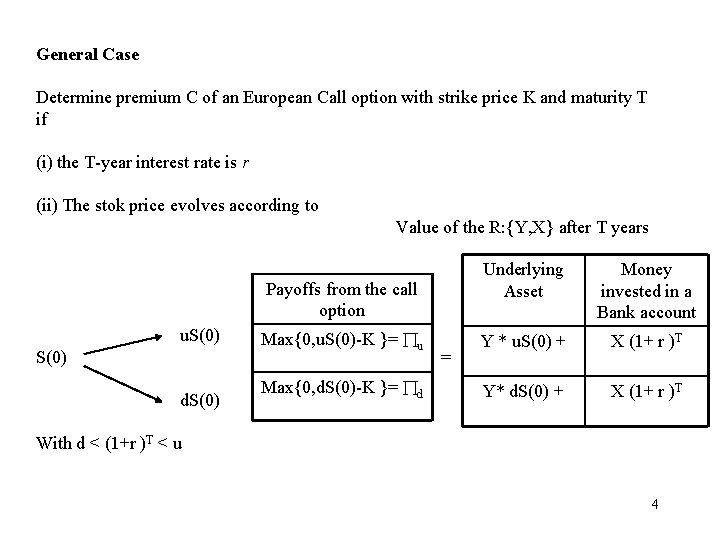
General Case Determine premium C of an European Call option with strike price K and maturity T if (i) the T-year interest rate is r (ii) The stok price evolves according to Value of the R: {Y, X} after T years Underlying Asset Money invested in a Bank account Max{0, u. S(0)-K }= u = Y * u. S(0) + X (1+ r )T Max{0, d. S(0)-K }= d Y* d. S(0) + X (1+ r )T Payoffs from the call option u. S(0) d. S(0) With d < (1+r )T < u 4

The composition of the replicating portfolio is given by the solution of the system u = Y u S(0) + X(1+ r)T d = Y d S(0) + X(1+ r)T Conclusion: The no arbitrage price for the call is C = Y* S(0) + X = 5

Risk Neutral Valuation That can also be written as where 6
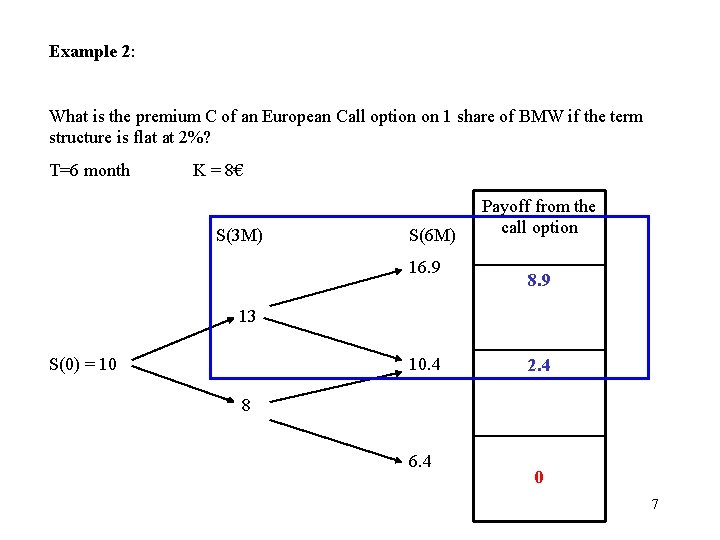
Example 2: What is the premium C of an European Call option on 1 share of BMW if the term structure is flat at 2%? T=6 month K = 8€ S(3 M) S(6 M) 16. 9 Payoff from the call option 8. 9 13 S(0) = 10 10. 4 2. 4 8 6. 4 0 7

Replicating portfolio R 1: {Y, X} = {1, -7. 96} Value of the option C 1 = 1*13 – 7. 96 = € 5. 04 Payoff from the call option u = 1. 3 d = 0. 8 S(3 M) S(6 M) 16. 9 8. 9 10. 4 2. 4 13 8
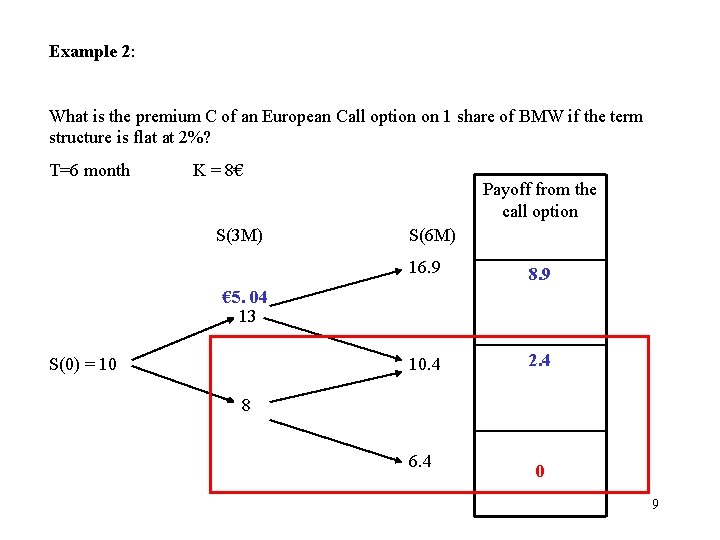
Example 2: What is the premium C of an European Call option on 1 share of BMW if the term structure is flat at 2%? T=6 month K = 8€ Payoff from the call option S(3 M) S(6 M) 16. 9 8. 9 10. 4 2. 4 € 5. 04 13 S(0) = 10 8 6. 4 0 9
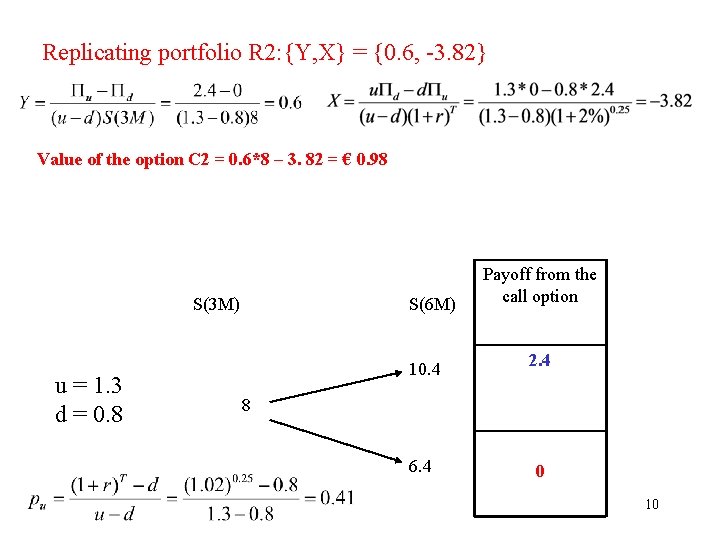
Replicating portfolio R 2: {Y, X} = {0. 6, -3. 82} Value of the option C 2 = 0. 6*8 – 3. 82 = € 0. 98 S(3 M) u = 1. 3 d = 0. 8 S(6 M) Payoff from the call option 10. 4 2. 4 6. 4 0 8 10
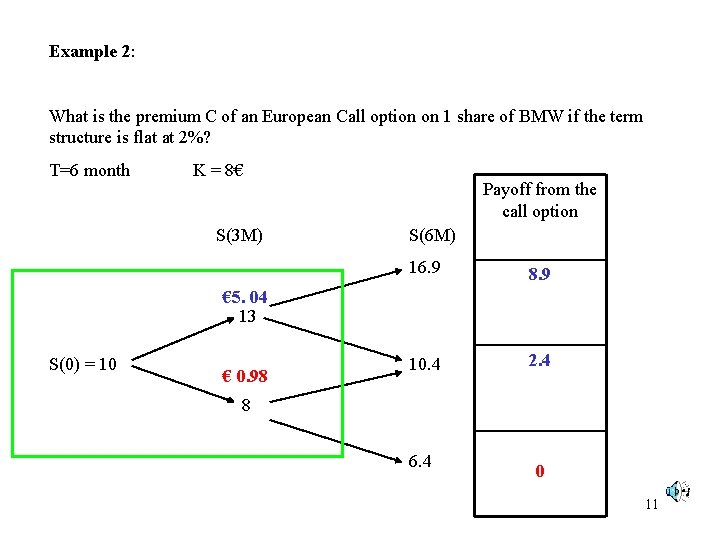
Example 2: What is the premium C of an European Call option on 1 share of BMW if the term structure is flat at 2%? T=6 month K = 8€ Payoff from the call option S(3 M) S(6 M) 16. 9 8. 9 10. 4 2. 4 € 5. 04 13 S(0) = 10 € 0. 98 8 6. 4 0 11
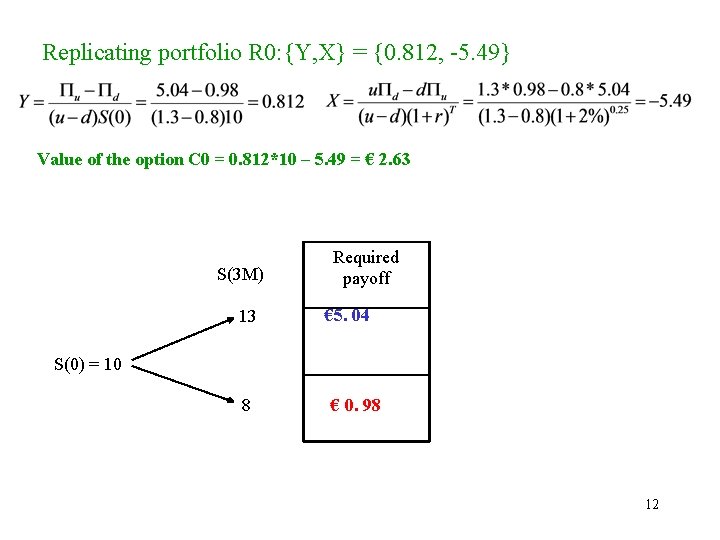
Replicating portfolio R 0: {Y, X} = {0. 812, -5. 49} Value of the option C 0 = 0. 812*10 – 5. 49 = € 2. 63 S(3 M) 13 Required payoff € 5. 04 S(0) = 10 8 € 0. 98 12
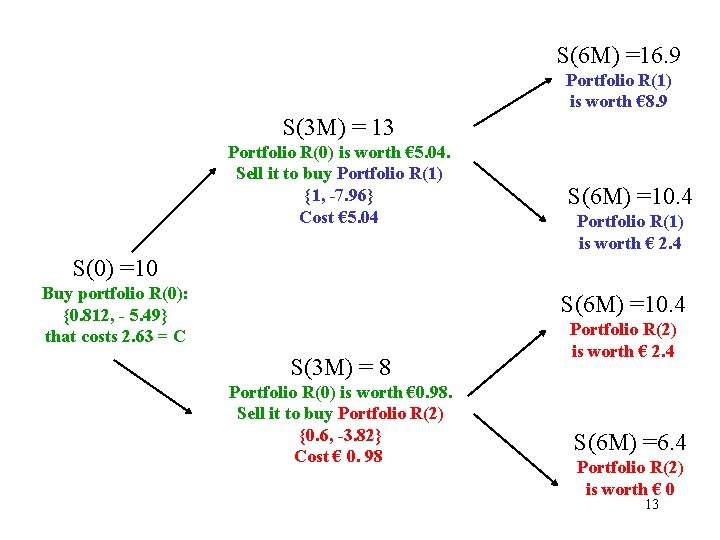
S(6 M) =16. 9 Portfolio R(1) is worth € 8. 9 S(3 M) = 13 Portfolio R(0) is worth € 5. 04. Sell it to buy Portfolio R(1) {1, -7. 96} Cost € 5. 04 S(6 M) =10. 4 Portfolio R(1) is worth € 2. 4 S(0) =10 Buy portfolio R(0): {0. 812, - 5. 49} that costs 2. 63 = C S(6 M) =10. 4 S(3 M) = 8 Portfolio R(0) is worth € 0. 98. Sell it to buy Portfolio R(2) {0. 6, -3. 82} Cost € 0. 98 Portfolio R(2) is worth € 2. 4 S(6 M) =6. 4 Portfolio R(2) is worth € 0 13
General case 14

CONCLUSION • Definition of put and call European and American options. • Exercise decision and payoffs of options • Portfolios of options/ trading strategies. • Put-Call Parity • Bottom vertical Straddle • Butterfly spread • … • Upper and lower bounds for C and P. • No arbitrage option price when the underlying asset price follows a binomial tree 15
- Slides: 15