Options Introduction Call and put option contracts Notation

Options Introduction Call and put option contracts Notation Definitions Graphical representations (payoff diagrams) Finance 30233, Fall 2011 Advanced Investments S. Mann The Neeley School at TCU

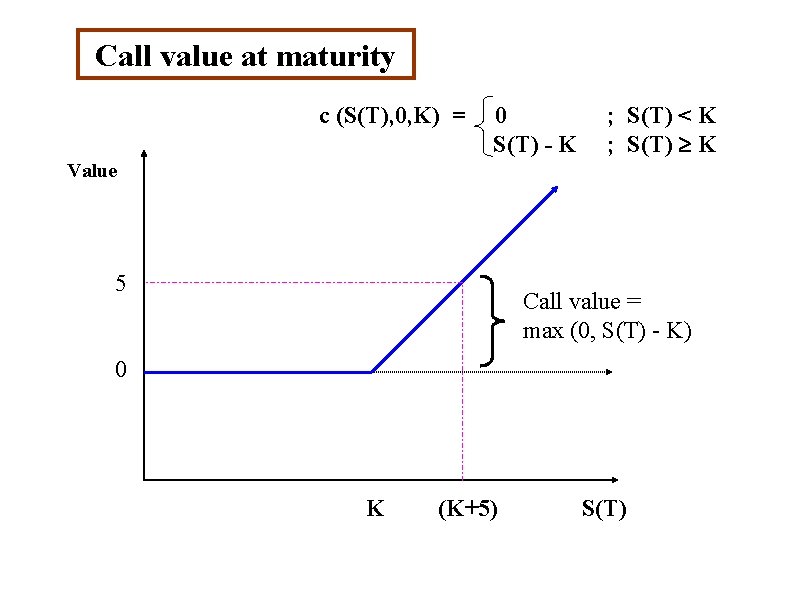
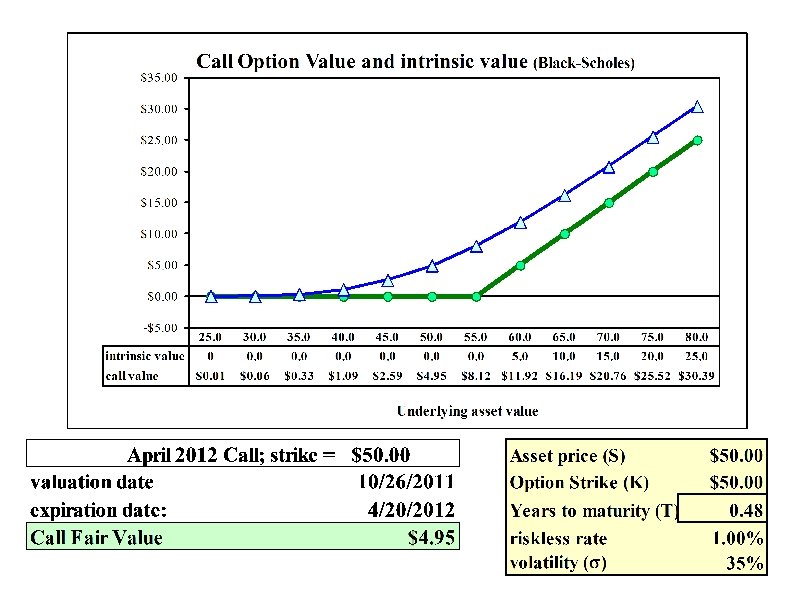
Options Right, but not the obligation, to either buy or sell at a fixed price over a time period (t, T) Call option - right to buy at fixed price Put option - right to sell at fixed price (K) : strike price, exercise price (K = X in BKM) selling an option: write the option Notation: call value (stock price, time remaining, strike price) = c ( S(t) , T-t, K) at expiration (T): c (S(T), 0, K) = 0 if S(T) < K S(T) - K if S(T) K or: c(S(T), 0, K) = max (0, S(T) - K)

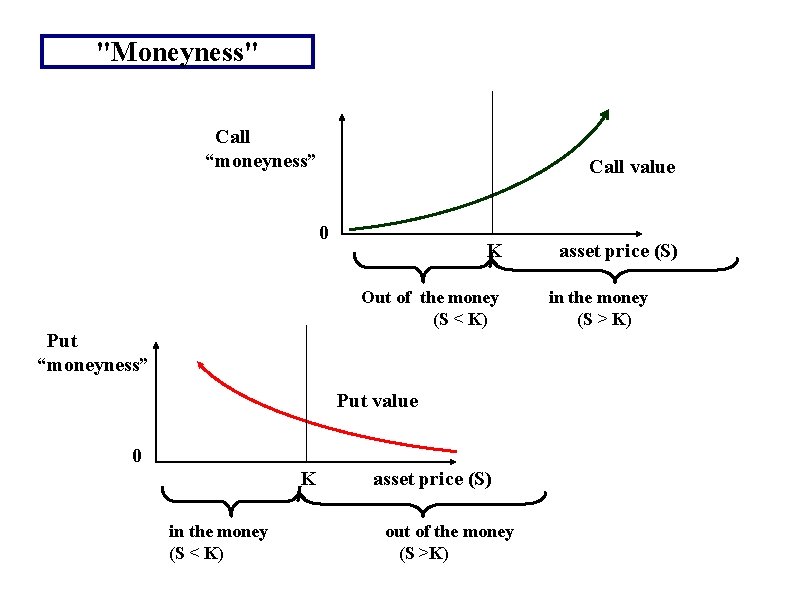
"Moneyness" Call “moneyness” Call value 0 K Out of the money (S < K) Put “moneyness” Put value 0 K in the money (S < K) asset price (S) out of the money (S >K) asset price (S) in the money (S > K)

Call value at maturity c (S(T), 0, K) = 0 S(T) - K ; S(T) < K ; S(T) K Value 5 Call value = max (0, S(T) - K) 0 K (K+5) S(T)

Short position in Call: value at maturity c (S(T), 0, K) = Value 0 S(T) - K short is opposite: -c(S(T), 0, K) = 0 -[S(T)-K] 0 ; S(T) < K ; S(T) K Short call value = min (0, K -S(T)) -5 K (K+5) S(T)

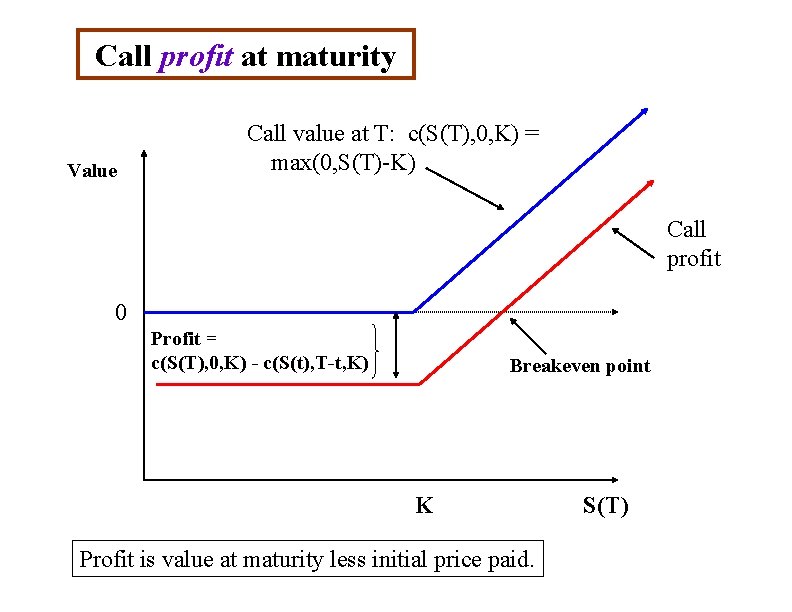
Call profit at maturity Value Call value at T: c(S(T), 0, K) = max(0, S(T)-K) Call profit 0 Profit = c(S(T), 0, K) - c(S(t), T-t, K) Breakeven point K Profit is value at maturity less initial price paid. S(T)

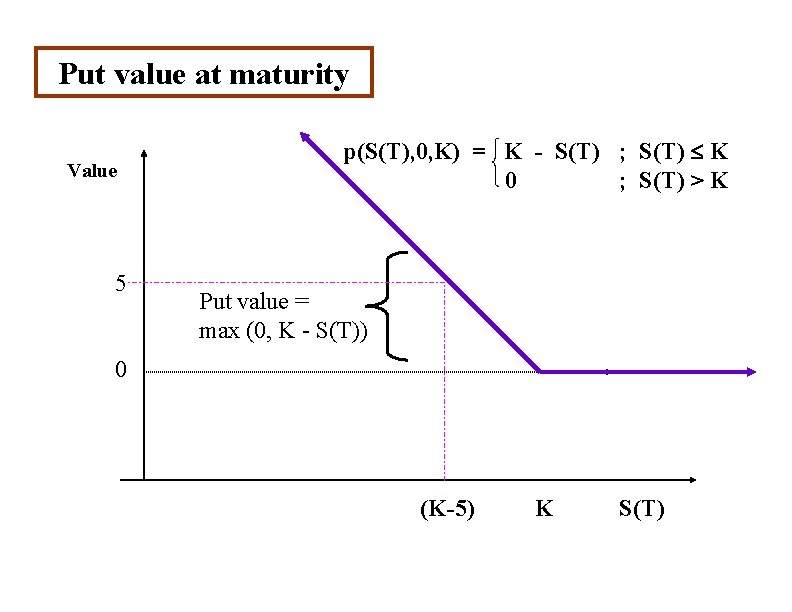
Put value at maturity Value 5 p(S(T), 0, K) = K - S(T) ; S(T) K 0 ; S(T) > K Put value = max (0, K - S(T)) 0 (K-5) K S(T)

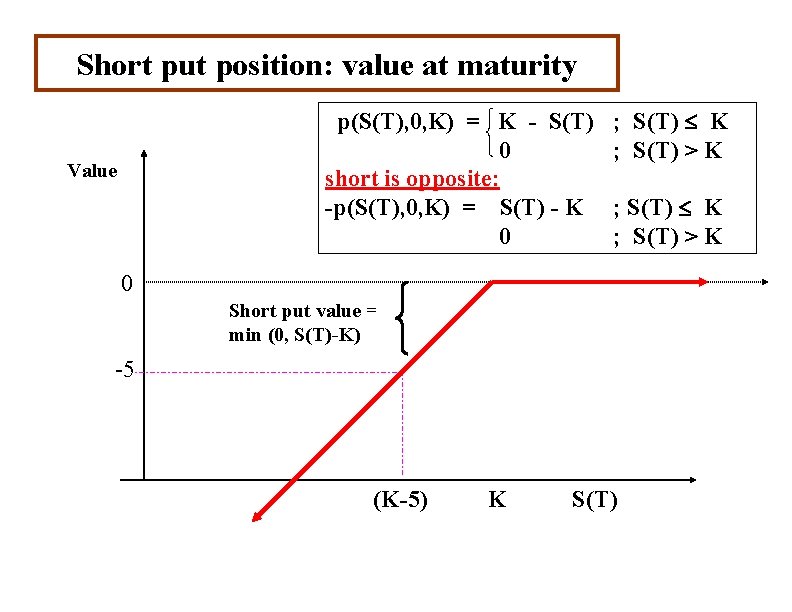
Short put position: value at maturity p(S(T), 0, K) = K - S(T) 0 short is opposite: -p(S(T), 0, K) = S(T) - K 0 Value ; S(T) K ; S(T) > K 0 Short put value = min (0, S(T)-K) -5 (K-5) K S(T)

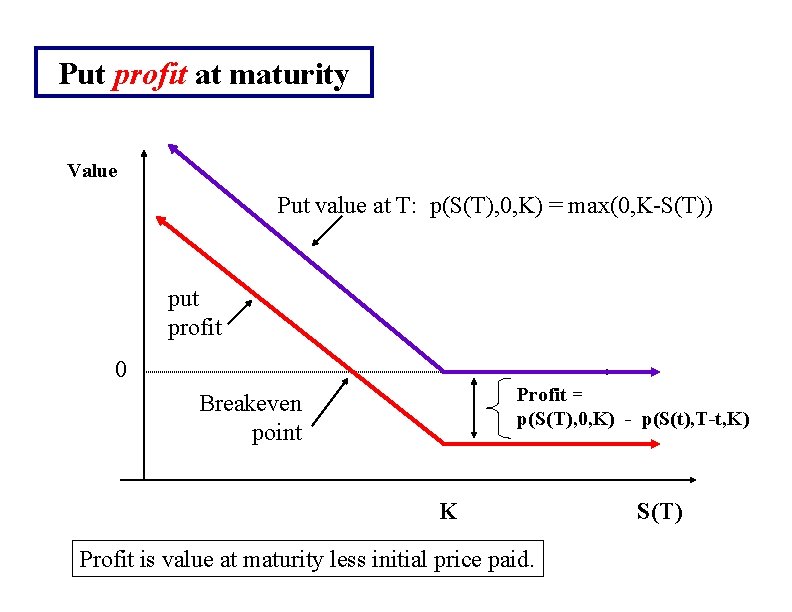
Put profit at maturity Value Put value at T: p(S(T), 0, K) = max(0, K-S(T)) put profit 0 Profit = p(S(T), 0, K) - p(S(t), T-t, K) Breakeven point K Profit is value at maturity less initial price paid. S(T)

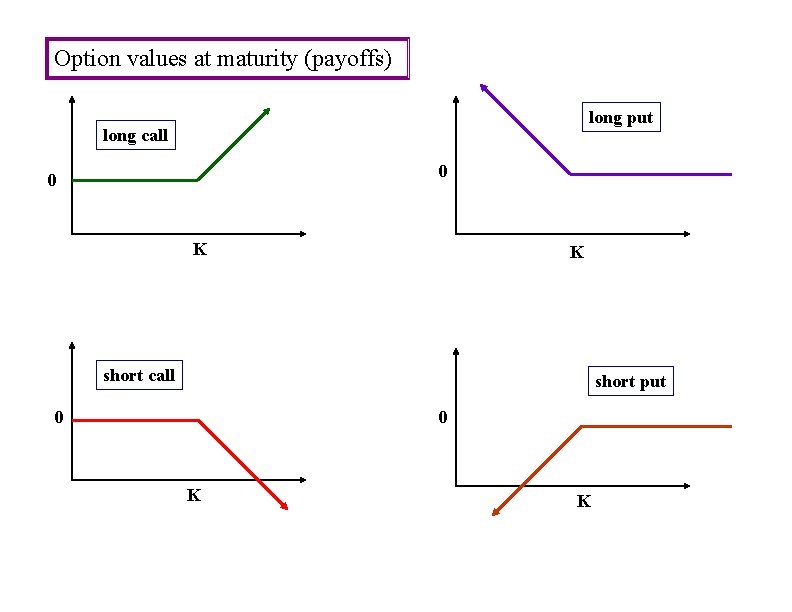
Option values at maturity (payoffs) long put long call 0 0 K K short call short put 0 0 K K

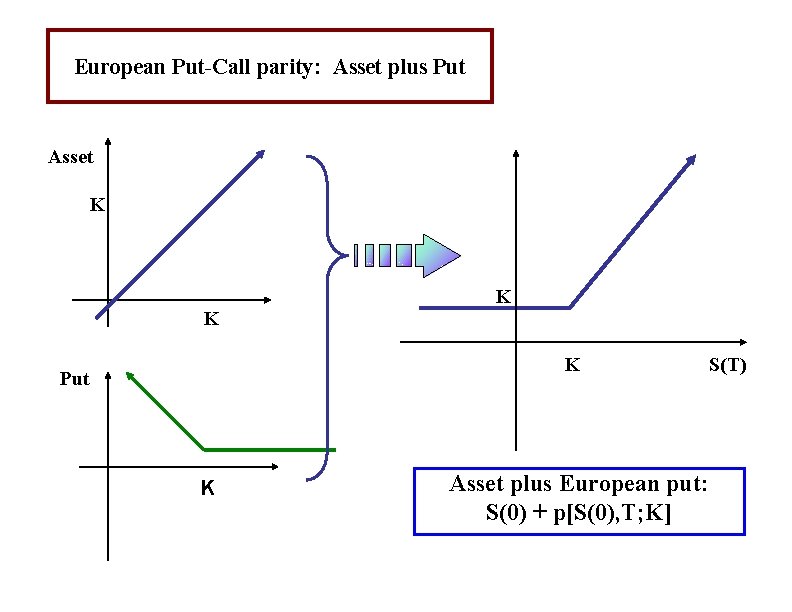
European Put-Call parity: Asset plus Put Asset K K Put K Asset plus European put: S(0) + p[S(0), T; K] S(T)

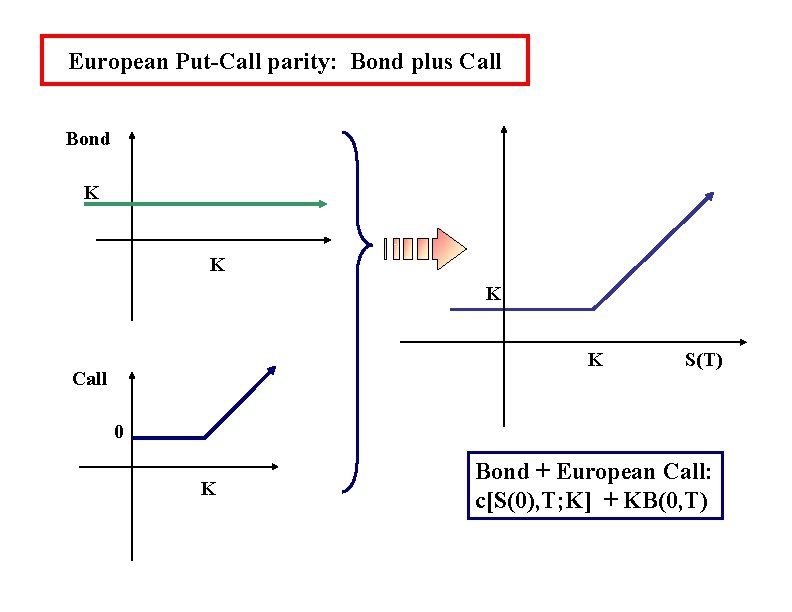
European Put-Call parity: Bond plus Call Bond K K Call S(T) 0 K Bond + European Call: c[S(0), T; K] + KB(0, T)

European Put-Call parity Position Portfolio A: Stock put total A: Portfolio B: Call Bill total B: cost now Value at expiration S(T) K S(T) > K S(0) p[S(0), T; K] S+P S(T) K - S(T) K S(T) 0 S (T) c[S(0), T; K] KB(0, T) C + KB(0, T) 0 K K S(T) - K K S(T) European Put-Call parity: S(0) + p[S(0), T; K] = c[S(0), T; K] + KB(0, T)

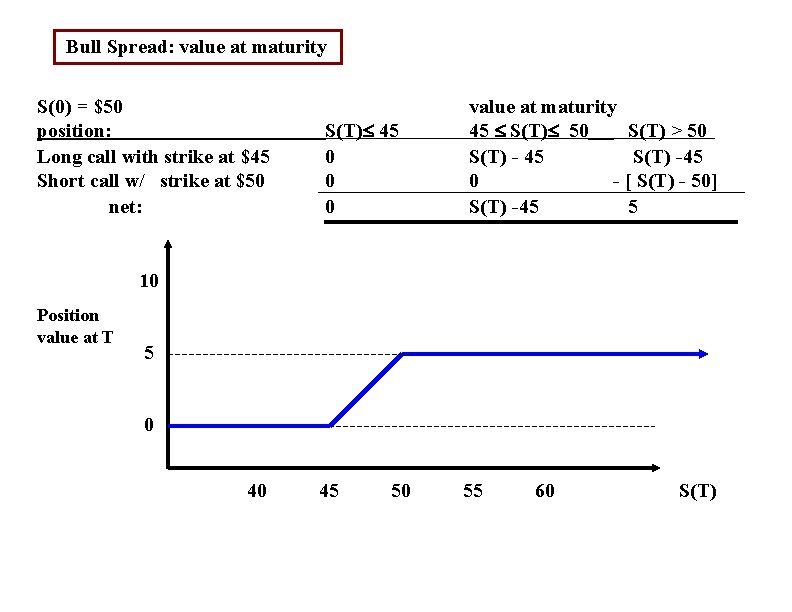
Bull Spread: value at maturity S(0) = $50 position: Long call with strike at $45 Short call w/ strike at $50 net: S(T) 45 0 0 0 value at maturity 45 S(T) 50 S(T) > 50 S(T) - 45 S(T) -45 0 - [ S(T) - 50] S(T) -45 5 10 Position value at T 5 0 40 45 50 55 60 S(T)

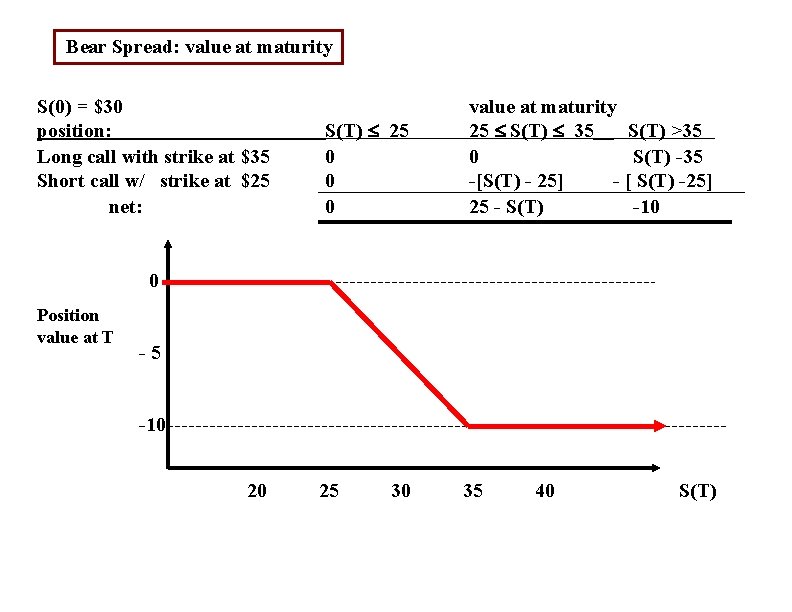
Bear Spread: value at maturity S(0) = $30 position: Long call with strike at $35 Short call w/ strike at $25 net: S(T) 25 0 0 0 value at maturity 25 S(T) 35 S(T) >35 0 S(T) -35 -[S(T) - 25] - [ S(T) -25] 25 - S(T) -10 0 Position value at T -5 -10 20 25 30 35 40 S(T)

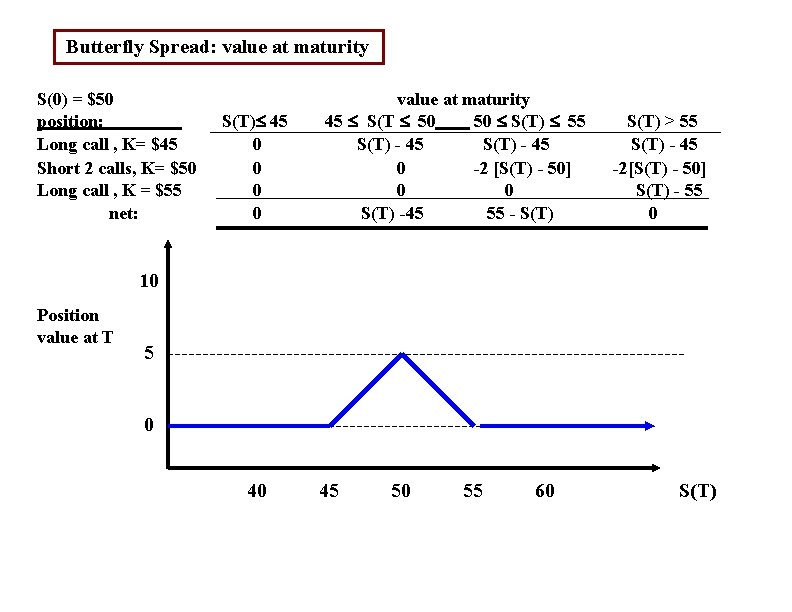
Butterfly Spread: value at maturity S(0) = $50 position: Long call , K= $45 Short 2 calls, K= $50 Long call , K = $55 net: S(T) 45 0 0 value at maturity 45 S(T 50 50 S(T) 55 S(T) - 45 0 -2 [S(T) - 50] 0 0 S(T) -45 55 - S(T) > 55 S(T) - 45 -2[S(T) - 50] S(T) - 55 0 10 Position value at T 5 0 40 45 50 55 60 S(T)

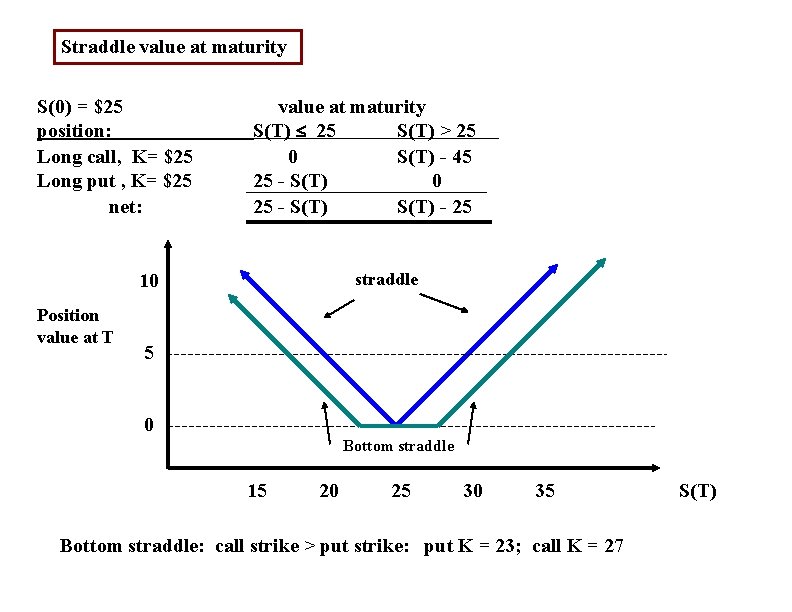
Straddle value at maturity S(0) = $25 position: Long call, K= $25 Long put , K= $25 net: value at maturity S(T) 25 S(T) > 25 0 S(T) - 45 25 - S(T) 0 25 - S(T) - 25 straddle 10 Position value at T 5 0 Bottom straddle 15 20 25 30 35 Bottom straddle: call strike > put strike: put K = 23; call K = 27 S(T)