OPTIMUM TRANSMIT ARCHITECTURE OF A MIMO SYSTEM UNDER

OPTIMUM TRANSMIT ARCHITECTURE OF A MIMO SYSTEM UNDER MODULUS CHANNEL KNOWLEDGE AT THE TRANSMITTER u Miquel Payaró u Xavier Mestre u Ana Pérez u Miguel A. Lagunas u CENTRE TECNOLÒGIC de TELECOMUNICACIONS de CATALUNYA u CTTC Miquel Payaró | NEWCOM Meeting

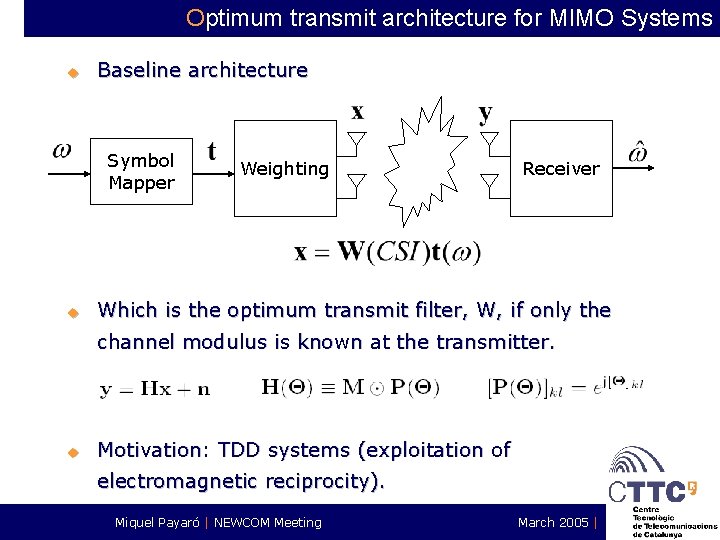
Optimum transmit architecture for MIMO Systems u u If perfect CSI is assumed at the receiver end, the achievable rates of a MIMO system depend on the quality and quantity of CSI available at the transmitter side. Generic effect of partial side information in MIMO Systems [Skoglund]. Capacity can be achieved by a structure that first maps source symbols into space time codewords independently from CSI and then weights these codewords as a function of CSI Symbol Mapper Weighting Miquel Payaró | NEWCOM Meeting Receiver March 2005 |

Optimum transmit architecture for MIMO Systems u Baseline architecture Symbol Mapper u Weighting Receiver Which is the optimum transmit filter, W, if only the channel modulus is known at the transmitter. u Motivation: TDD systems (exploitation of electromagnetic reciprocity). Miquel Payaró | NEWCOM Meeting March 2005 |

Optimum transmit architecture for MIMO Systems u We are interested in maximizing the mutual information between the transmitted and the received signals. For a particular realization of the flat-fading channel matrix, H, the mutual information is given by u We wish to find the covariance matrix that maximizes the mutual information averaged over the statistics of the unknown part of the incomplete CSI Miquel Payaró | NEWCOM Meeting March 2005 |

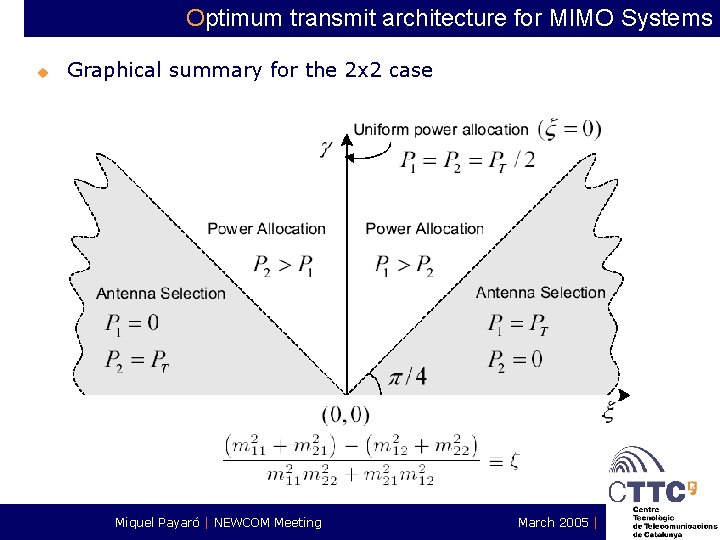
Optimum transmit architecture for MIMO Systems u First result: we prove that power allocation is a capacity achieving structure in this situation. u Second result: we give a description of the optimum power allocation strategy in the 2 x 2 case. Antenna selection SNR at the receiver u Otherwise: power allocation (roots of a fourth order polynomial) Miquel Payaró | NEWCOM Meeting March 2005 |

Optimum transmit architecture for MIMO Systems u Graphical summary for the 2 x 2 case Miquel Payaró | NEWCOM Meeting March 2005 |

Optimum transmit architecture for MIMO Systems • Technical problems: • No great capacity improvement in rayleigh i. i. d. flat fading channels w. r. t. uniform power allocation. • • Closed form analysis limited to the flat fading 2 x 2 case. For the general case, numerical solutions are computationally hard to obtain. • Possible solutions: • Formulation extension to frequency-selective channels. • Performance improvement w. r. t. uniform power allocation. • Maximin approach closed form solution for the 2 x n flat fading case. • Numerical solutions are computationally simpler to obtain. Miquel Payaró | NEWCOM Meeting March 2005 |

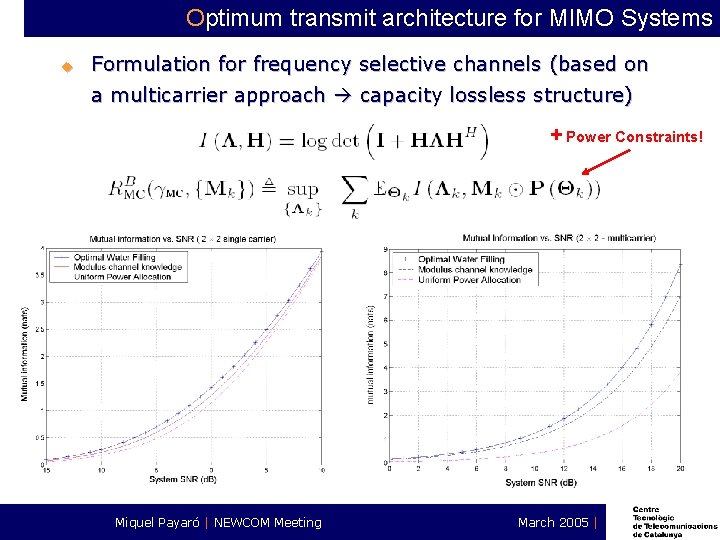
Optimum transmit architecture for MIMO Systems u Formulation for frequency selective channels (based on a multicarrier approach capacity lossless structure) + Power Constraints! Miquel Payaró | NEWCOM Meeting March 2005 |

Optimum transmit architecture for MIMO Systems u Maximin formulation u Closed form solution for the 2 x n case Miquel Payaró | NEWCOM Meeting March 2005 |

Optimum transmit architecture for MIMO Systems u In the maximin formulation, we can make use of the following approximation (exact when min(n. R, n. T) = 2) u Single carrier problem formulation u Multicarrier problem formulation u In both cases, the solution can be computed very efficiently! Miquel Payaró | NEWCOM Meeting March 2005 |

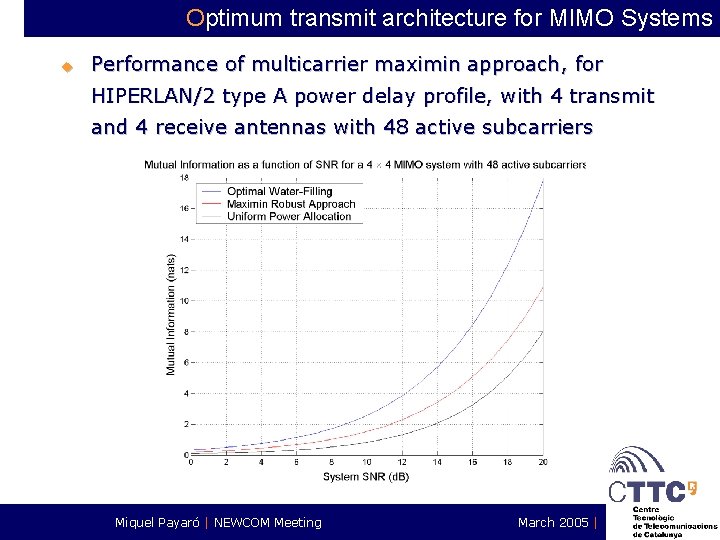
Optimum transmit architecture for MIMO Systems u Performance of multicarrier maximin approach, for HIPERLAN/2 type A power delay profile, with 4 transmit and 4 receive antennas with 48 active subcarriers Miquel Payaró | NEWCOM Meeting March 2005 |