Optimizing pooling strategies for the massive nextgeneration sequencing

Optimizing pooling strategies for the massive next-generation sequencing of viral samples Pavel Skums 1 Joint work with Olga Glebova 2, Alex Zelikovsky 2, Ion Mandoiu 3 and Yury Khudyakov 1 1 Centers for Disease Control and Prevention, Atlanta, GA 2 Georgia State University, Atlanta, GA 3 University of Connecticut, Storrs, CT

Outline 1. Massive NGS of viral samples 2. Optimal pooling design problem 3. Algorithm and results

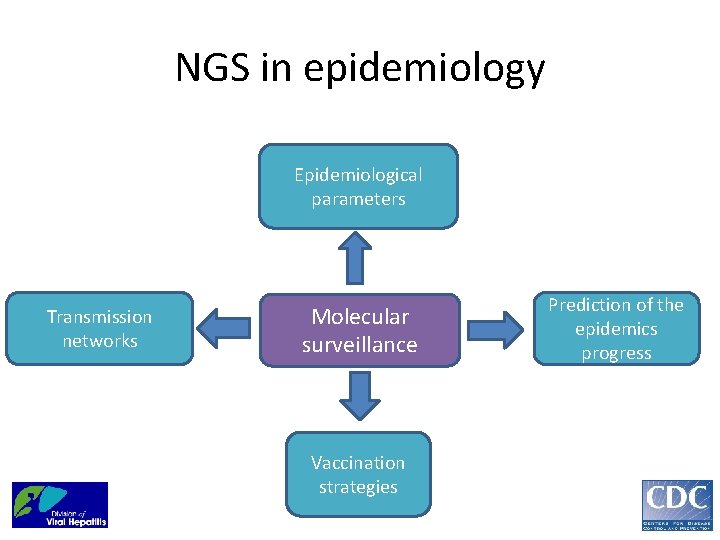
NGS in epidemiology Epidemiological parameters Transmission networks Molecular surveillance Vaccination strategies Prediction of the epidemics progress

NGS in epidemiology A large-scale molecular surveillance requires sequencing of unprecedentedly large sets of viral samples. NGS of tens of thousands of samples is highly cost- and laborintensive. Example: sequencing 100 K samples using 454 senior system with 50 MIDs doing one sequencing run per day Cost: 5000*(100 000)/50 = 10 000$ Time: (100 000)/50 = 2000 days 5. 5 years

Optimal Pooling Design Problem Goal: a framework for identification of viral sequences from large number of samples using the smallest possible number of NGS runs. Idea: for n samples generate m pools (i. e. mixtures of samples) with m << n in such a way that every sample is uniquely identified by the pools to which it belongs.

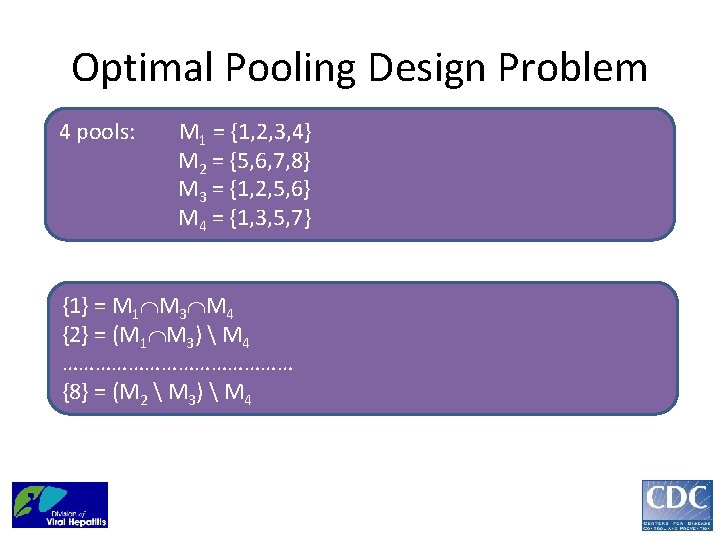
E Optimal Pooling Design Problem Example. 8 samples: 1, 2, 3, 4, 5, 6, 7, 8 Sequencing each sample separately: 8 runs 4 pools: M 1 = {1, 2, 3, 4} M 2 = {5, 6, 7, 8} M 3 = {1, 2, 5, 6} M 4 = {1, 3, 5, 7} Sequencing pools: 4 runs

Optimal Pooling Design Problem 4 pools: M 1 = {1, 2, 3, 4} M 2 = {5, 6, 7, 8} M 3 = {1, 2, 5, 6} M 4 = {1, 3, 5, 7} {1} = M 1 M 3 M 4 {2} = (M 1 M 3) M 4 ………………… {8} = (M 2 M 3) M 4

Optimal Pooling Design Problem 1 (Optimal Pooling Design Problem). Given: a set of samples S = {S 1, . . . , Sn} Find: a set of pools P = {P 1, …, Pm} , Pk S for k=1, …, m such that 1)P 1 …Pm = S 2) for every Si, Sj S there exists Pk P such that (Pk separates Si and Sj) |Pk {Si, Sj}| = 1 3) m is minimal Theorem 1. There exists a solution of Problem 1 with m = log(n) + 1

Optimal Pooling Design Problem Additional conditions for the problem Condition Reasons Each pool contains at most k samples • number of reads which could be obtained by each NGS technology is bounded • if large number of samples are mixed in one pool, some of them may be lost due to a PCR bias |Pj| ≤ k for j = 1, …, m

Optimal Pooling Design Problem Additional conditions for the problem Condition Reasons Each pool contains at most k samples • number of reads which could be obtained by each NGS technology is bounded • if large number of samples are mixed in one pool, some of them may be lost due to a PCR bias |Pj| ≤ k for j = 1, …, m Each sample belongs to at least l pools |{j : Si Pj}| ≥ l for i = 1, …, n • to ensure sufficient coverage for sequences of each sample

Optimal Pooling Design Problem Additional conditions for the problem Condition Reasons Each pool contains at most k samples • number of reads which could be obtained by each NGS technology is bounded • if large number of samples are mixed in one pool, some of them may be lost due to a PCR bias |Pj| ≤ k for j = 1, …, m Each sample belongs to at least l pools • to ensure sufficient coverage for sequences of each sample |{j : Si Pj}| ≥ l for i = 1, …, n Some pairs of samples should not be put into a same pool • Some samples may intersect (if they belong to the same transmission cluster)

Optimal Pooling Design Problem A graph G(S) = (V, E), where V=S Si. Sj E if and only if there is a confidence that the samples Si and Sj do not intersect. Condition Reasons Each pool Pj should be a clique of the graph G(S) • Some samples may intersect (if they belong to the same transmission cluster)

Optimal Pooling Design Problem 2 (Minimum Clique Test Set Problem). Given: a graph G=G(S), natural numbers k, l Find: a set of cliques P = {P 1, …, Pm} of G such that 1) |Pi| ≤ k for every i=1, …, m 2) every vertex v V(G) belongs to at least l cliques from P 3) for every u, v V(G) there exists Pi P such that |Pi {u, v}| = 1 4) m is minimal

Optimal Pooling Design Problem Minimum Test Set Problem (Garey, Johnson) Given: collection Q={Q 1, …, Qn} of subsets of a finite set S Find: a subcollection P = {P 1, …, Pm} Q such that 1) for every si, sj S there exists Pr P such that |Pr {si, sj}| = 1 2) m is minimal

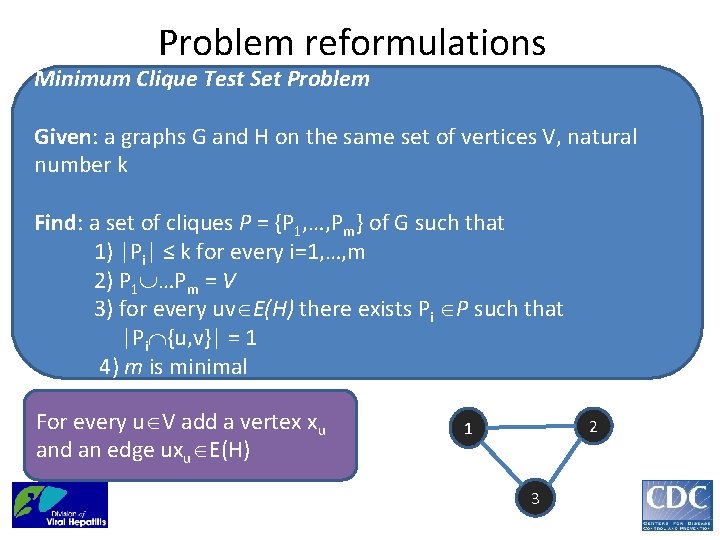
Problem reformulations Minimum Clique Test Set Problem Given: a graph G=G(S), natural numbers k, l Find: a set of cliques P = {P 1, …, Pm} of G such that 1) |Pi| ≤ k for every i=1, …, m 2) every vertex v V(G) belongs to at least l cliques from P 3) for every u, v V(G) there exists Pi P such that |Pi {u, v}| = 1 4) m is minimal Only some pairs of vertices should be separated A graph H with V(H)=V(G), uv E(H) if and only if u and v should be separated

Problem reformulations Minimum Clique Test Set Problem Given: a graphs G and H on the same set of vertices V, natural numbers k, l Find: a set of cliques P = {P 1, …, Pm} of G such that 1) |Pi| ≤ k for every i=1, …, m 2) every vertex v V(G) belongs to at least l cliques from P 3) for every uv E(H) there exists Pi P such that |Pi {u, v}| = 1 4) m is minimal Only some pairs of vertices should be separated A graph H with V(H)=V(G), uv E(H) if and only if u and v should be separated

Problem reformulations Minimum Clique Test Set Problem Given: a graphs G and H on the same set of vertices V, natural numbers k, l Find: a set of cliques P = {P 1, …, Pm} of G such that 1) |Pi| ≤ k for every i=1, …, m 2) every vertex v V belongs to at least l cliques from P 3) for every uv E(H) there exists Pi P such that |Pi {u, v}| = 1 4) m is minimal Replace each vertex v V(G) with l pairwise non-adjacent copies

Problem reformulations Minimum Clique Test Set Problem Given: a graphs G and H on the same set of vertices V, natural number k Find: a set of cliques P = {P 1, …, Pm} of G such that 1) |Pi| ≤ k for every i=1, …, m 2) P 1 …Pm = V(G) 3) for every uv E(H) there exists Pi P such that |Pi {u, v}| = 1 4) m is minimal Replace each vertex v V(G) with l pairwise non-adjacent copies

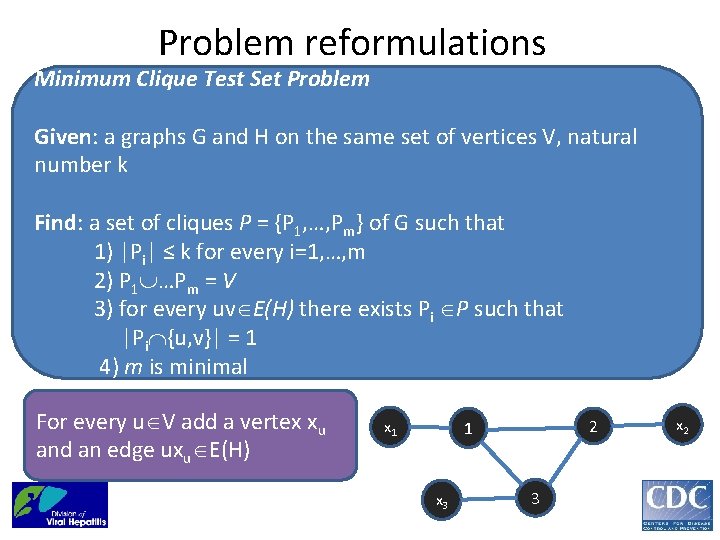
Problem reformulations Minimum Clique Test Set Problem Given: a graphs G and H on the same set of vertices V, natural number k Find: a set of cliques P = {P 1, …, Pm} of G such that 1) |Pi| ≤ k for every i=1, …, m 2) P 1 …Pm = V 3) for every uv E(H) there exists Pi P such that |Pi {u, v}| = 1 4) m is minimal For every u V add a vertex xu and an edge uxu E(H) 2 1 3

Problem reformulations Minimum Clique Test Set Problem Given: a graphs G and H on the same set of vertices V, natural number k Find: a set of cliques P = {P 1, …, Pm} of G such that 1) |Pi| ≤ k for every i=1, …, m 2) P 1 …Pm = V 3) for every uv E(H) there exists Pi P such that |Pi {u, v}| = 1 4) m is minimal For every u V add a vertex xu and an edge uxu E(H) 2 1 x 3 3 x 2

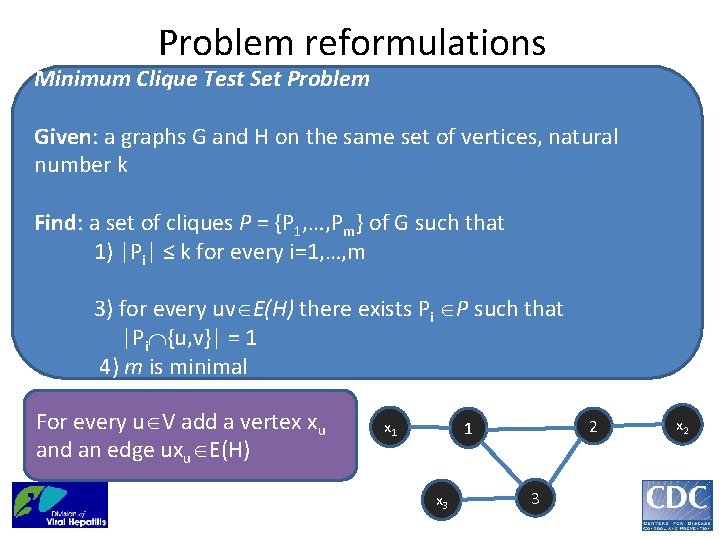
Problem reformulations Minimum Clique Test Set Problem Given: a graphs G and H on the same set of vertices, natural number k Find: a set of cliques P = {P 1, …, Pm} of G such that 1) |Pi| ≤ k for every i=1, …, m 3) for every uv E(H) there exists Pi P such that |Pi {u, v}| = 1 4) m is minimal For every u V add a vertex xu and an edge uxu E(H) 2 1 x 3 3 x 2

Heuristic algorithm Input: a graphs G and H on the same set of vertices V, natural number k P= WHILE C P C V OR E(H) find maximum cut (A, B) in H (using local search); for every a A put w(a) = # of neighbors of a from B in H; for every b B put w(b) = # of neighbors of b from A in H; find maximum clique C 1 with |C 1|≤k in a subgraph G[A] with weights w; find maximum clique C 2 with |C 2|≤k in a subgraph G[B] with weights w; C : = argmax{w(C 1), w(C 2)} ; P: = P {C}; E(H) : = E(H) {uv : u C, v VC} ENDWHILE

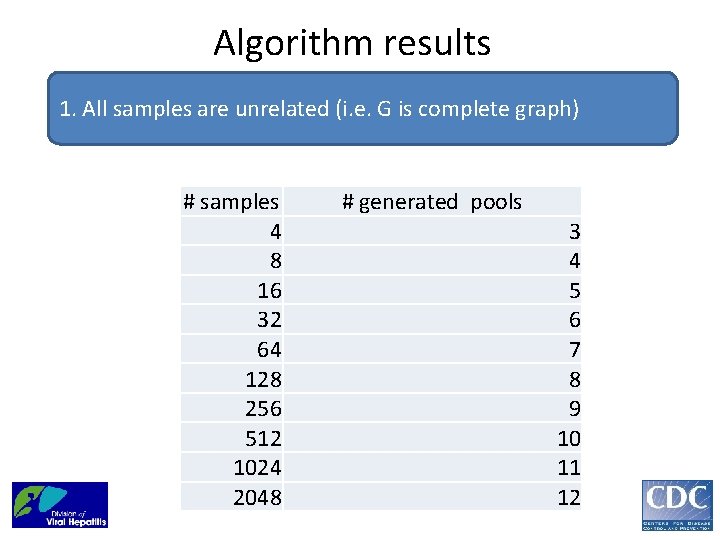
Algorithm results 1. All samples are unrelated (i. e. G is complete graph) # samples 4 8 16 32 64 128 256 512 1024 2048 # generated pools 3 4 5 6 7 8 9 10 11 12

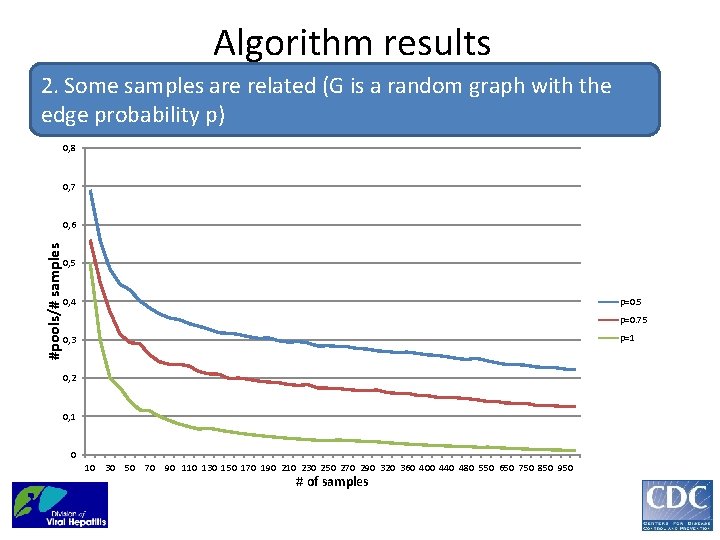
Algorithm results 2. Some samples are related (G is a random graph with the edge probability p) 0, 8 0, 7 #pools/# samples 0, 6 0, 5 0, 4 p=0. 5 p=0. 75 p=1 0, 3 0, 2 0, 1 0 10 30 50 70 90 110 130 150 170 190 210 230 250 270 290 320 360 400 440 480 550 650 750 850 950 # of samples

Thank you!