Optimizing number of hidden neurons in neural networks

Optimizing number of hidden neurons in neural networks IASTED International Conference on Artificial Intelligence and Applications Innsbruck, Austria Feb, 2007 Janusz A. Starzyk School of Electrical Engineering and Computer Science Ohio University Athens Ohio U. S. A 1

Outline l l l Neural networks – multi-layer perceptron Overfitting problem Signal-to-noise ratio figure (SNRF) Optimization using signal-to-noise ratio figure Experimental results Conclusions 2

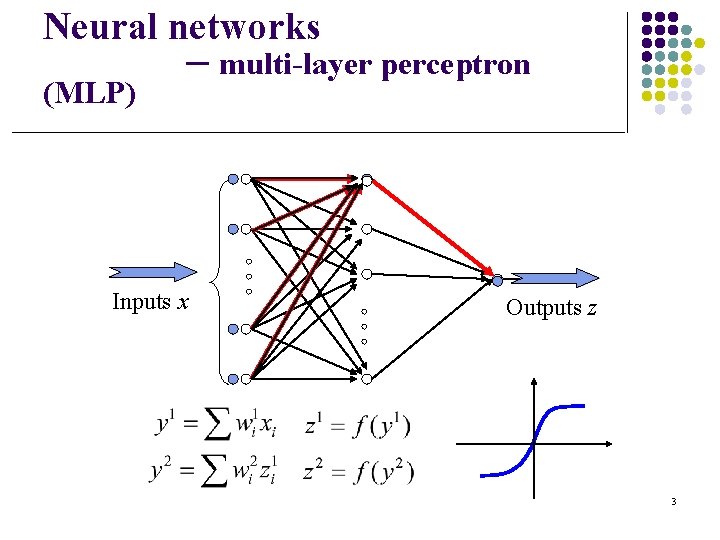
Neural networks (MLP) – multi-layer perceptron Inputs x Outputs z 3

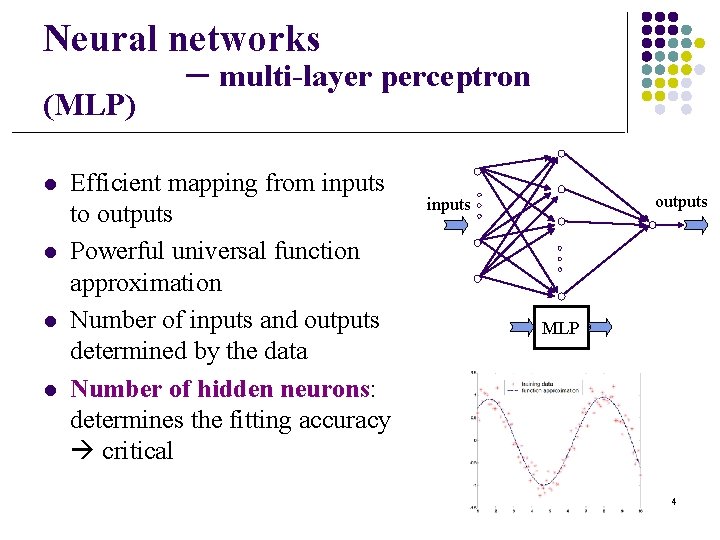
Neural networks (MLP) l l – multi-layer perceptron Efficient mapping from inputs to outputs Powerful universal function approximation Number of inputs and outputs determined by the data Number of hidden neurons: determines the fitting accuracy critical outputs inputs MLP 4

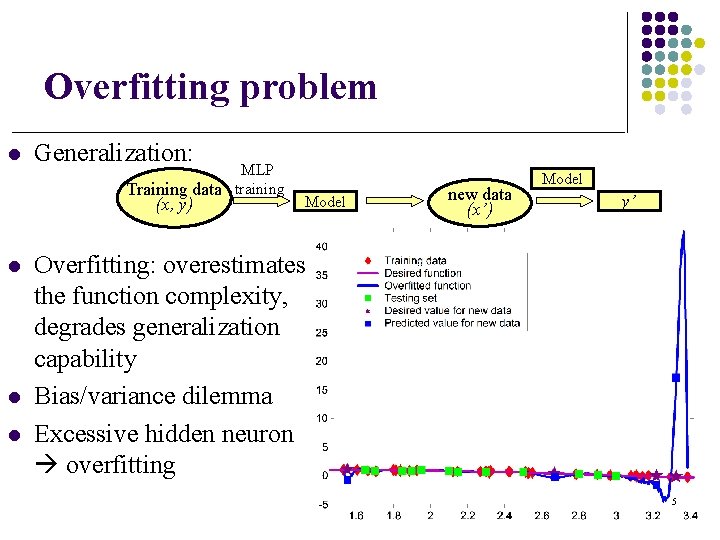
Overfitting problem l Generalization: MLP Training data training (x, y) l l l Model new data (x’) Model y’ Overfitting: overestimates the function complexity, degrades generalization capability Bias/variance dilemma Excessive hidden neuron overfitting 5

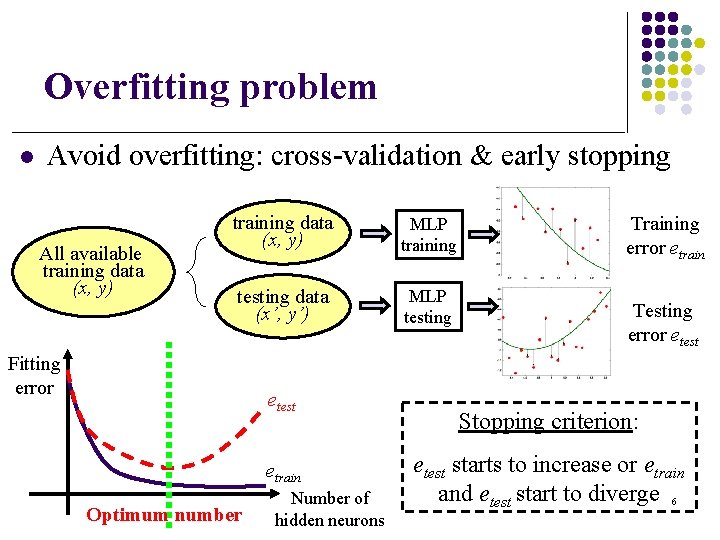
Overfitting problem l Avoid overfitting: cross-validation & early stopping All available training data (x, y) MLP training testing data (x’, y’) MLP testing Fitting error etest etrain Optimum number Number of hidden neurons Training error etrain Testing error etest Stopping criterion: etest starts to increase or etrain and etest start to diverge 6

Overfitting problem l l How to divide available data? When to stop? All available training data (x, y) etesting data (x’, y’) data wasted l Fitting error etrain Optimum number Number of hidden neurons Can test error catch the generalization error? 7

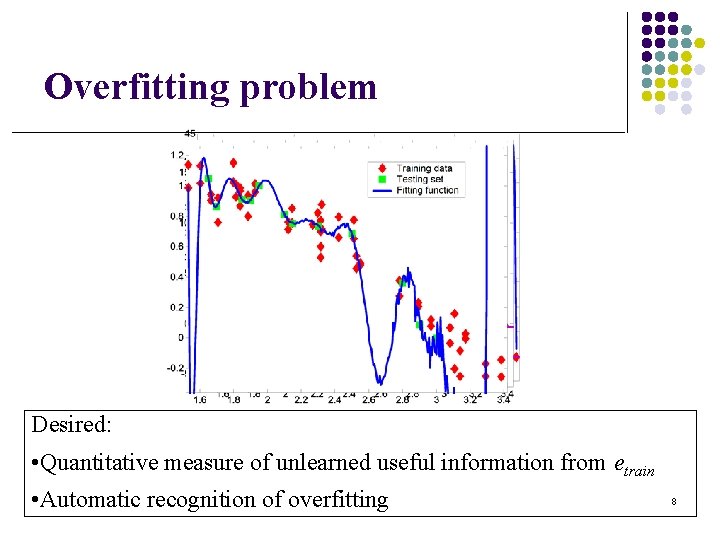
Overfitting problem Desired: • Quantitative measure of unlearned useful information from etrain • Automatic recognition of overfitting 8

Signal-to-noise ratio figure (SNRF) Sampled data: function value + noise l Error signal: approximation error component + noise component l Useful signal Should be reduced l l l Noise part Should not be learned Assumption: continuous function & WGN as noise Learning should stop – ? Signal-to-noise ratio figure (SNRF): If there is useful signal left unlearned If noise dominates in the error signal energy/noise energy Compare SNRFe and SNRFWGN 9

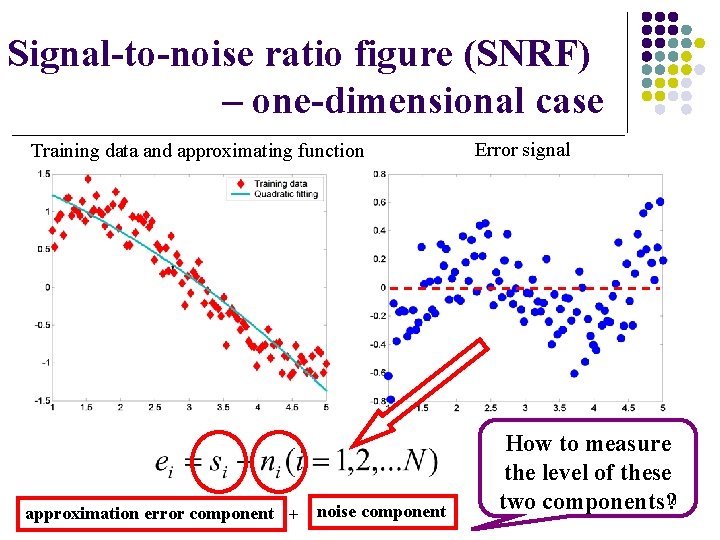
Signal-to-noise ratio figure (SNRF) – one-dimensional case Training data and approximating function approximation error component + noise component Error signal How to measure the level of these two components? 10

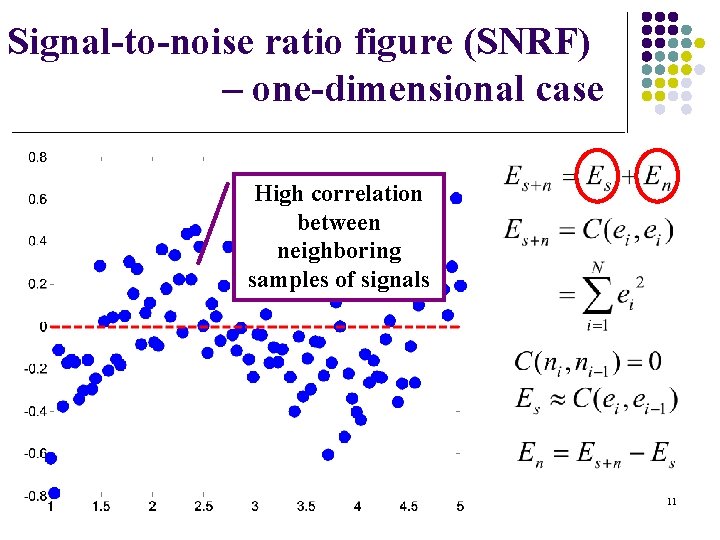
Signal-to-noise ratio figure (SNRF) – one-dimensional case High correlation between neighboring samples of signals 11

Signal-to-noise ratio figure (SNRF) – one-dimensional case 12

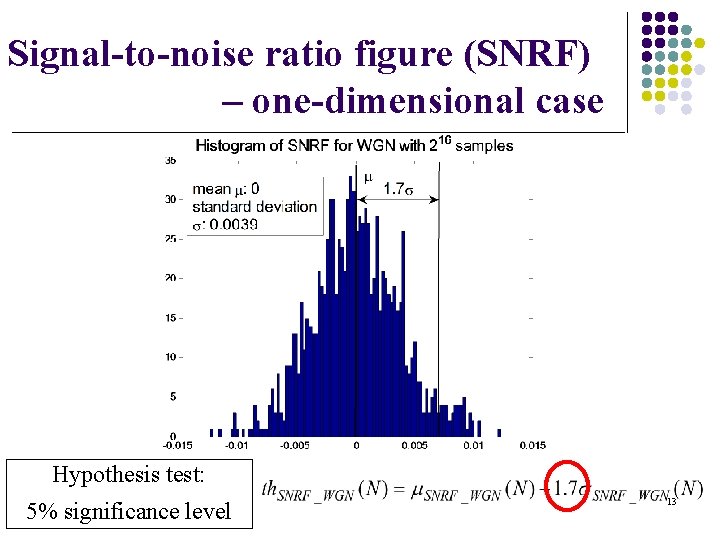
Signal-to-noise ratio figure (SNRF) – one-dimensional case Hypothesis test: 5% significance level 13

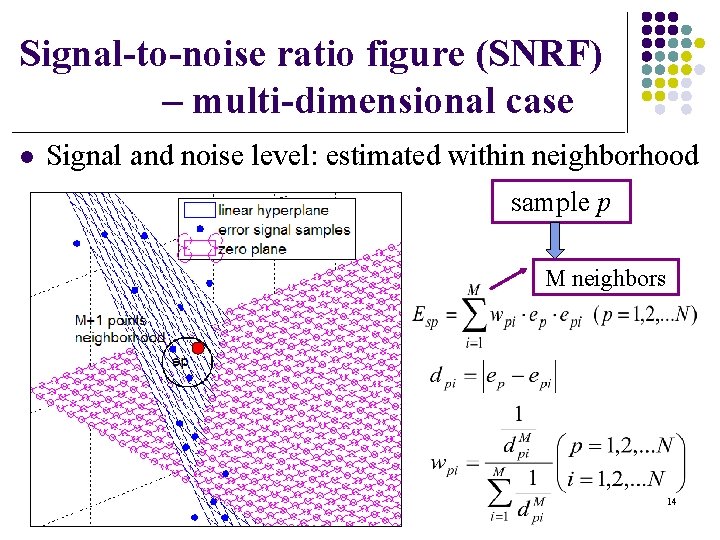
Signal-to-noise ratio figure (SNRF) – multi-dimensional case l Signal and noise level: estimated within neighborhood sample p M neighbors 14

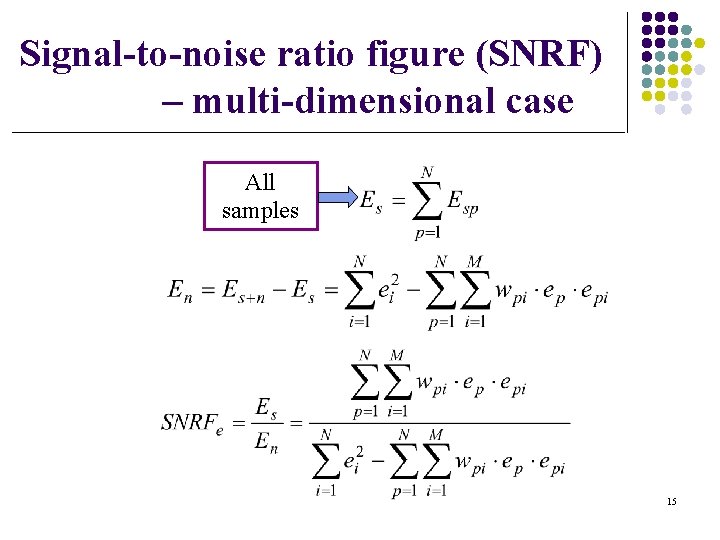
Signal-to-noise ratio figure (SNRF) – multi-dimensional case All samples 15

Signal-to-noise ratio figure (SNRF) – multi-dimensional case M=1 threshold multi-dimensional (M=1)≈ threshold one-dimensional 16

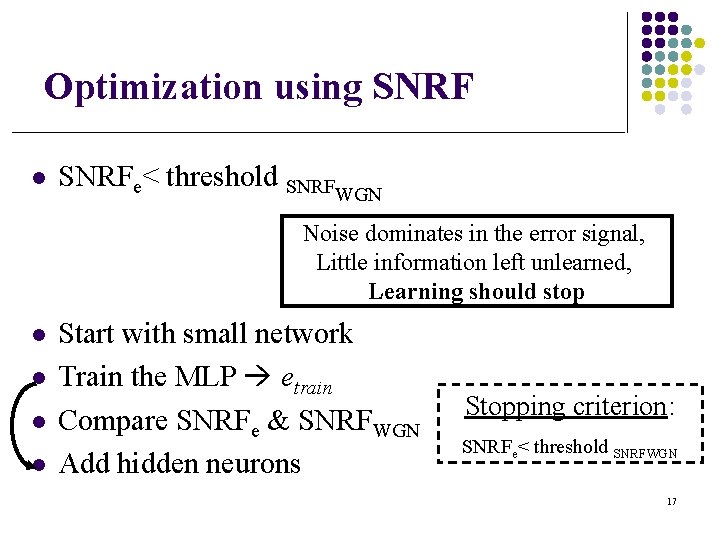
Optimization using SNRF l SNRFe< threshold SNRFWGN Noise dominates in the error signal, Little information left unlearned, Learning should stop l l Start with small network Train the MLP etrain Compare SNRFe & SNRFWGN Add hidden neurons Stopping criterion: SNRFe< threshold SNRFWGN 17

Optimization using SNRF Applied in optimizing number of iterations in back-propagation training to avoid overfitting (overtraining) l l Set the structure of MLP Train the MLP with back-propagation iteration etrain Compare SNRFe & SNRFWGN Keep training with more iterations 18

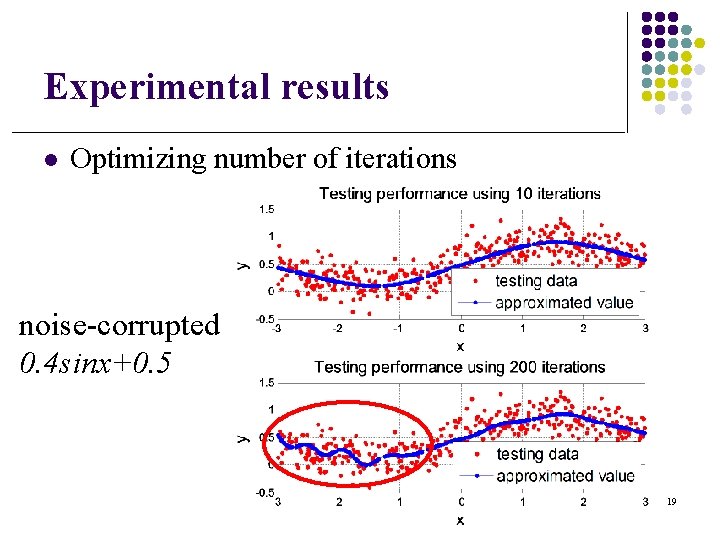
Experimental results l Optimizing number of iterations noise-corrupted 0. 4 sinx+0. 5 19

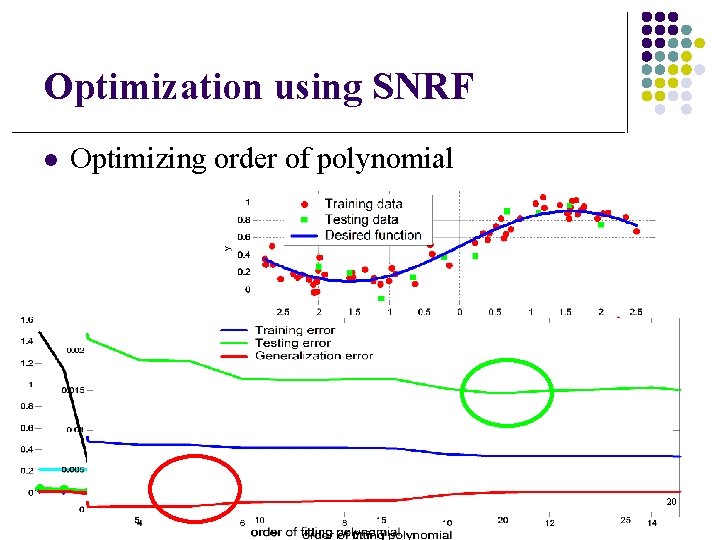
Optimization using SNRF l Optimizing order of polynomial 20

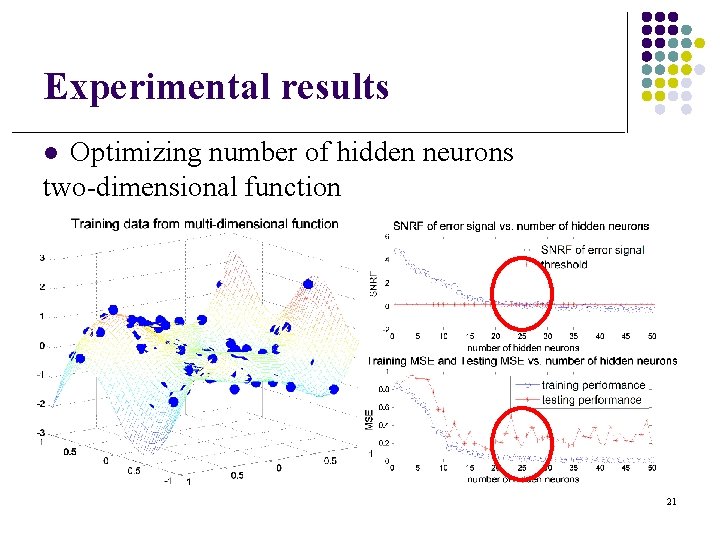
Experimental results Optimizing number of hidden neurons two-dimensional function l 21

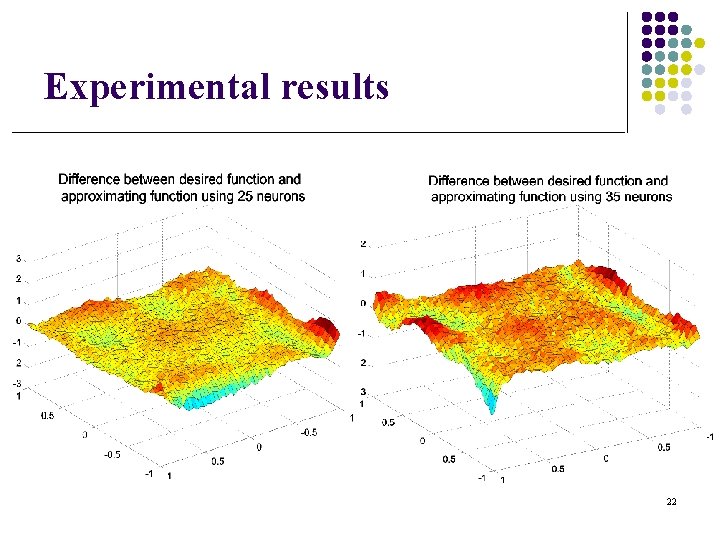
Experimental results 22

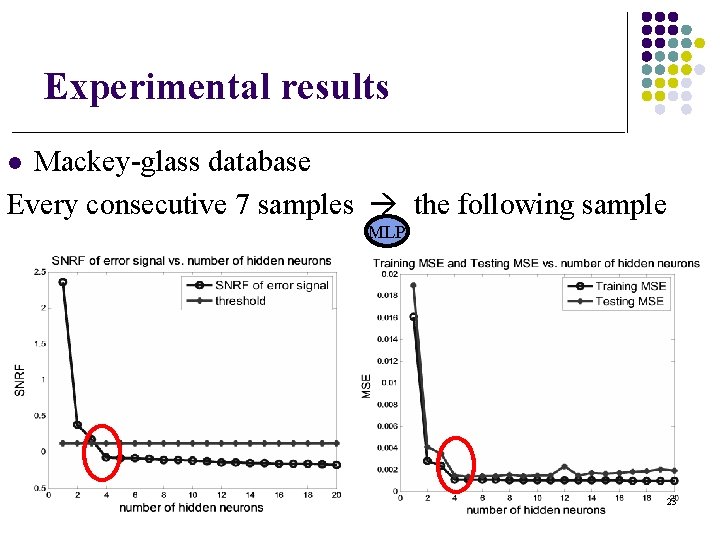
Experimental results Mackey-glass database Every consecutive 7 samples the following sample l MLP 23

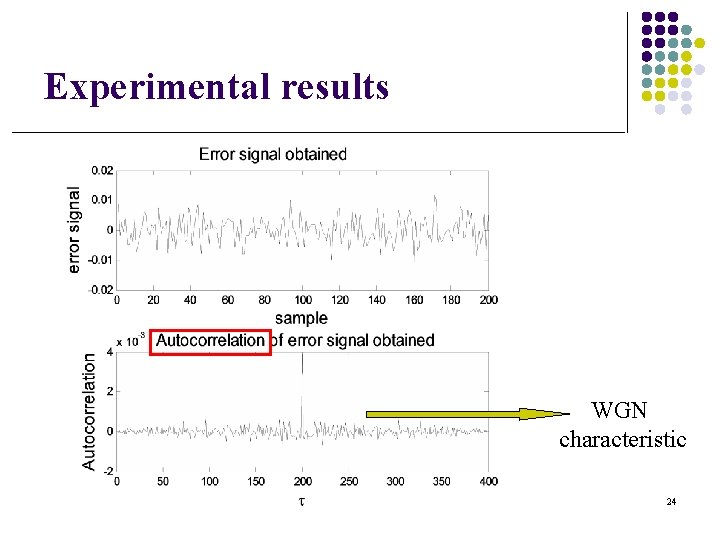
Experimental results WGN characteristic 24

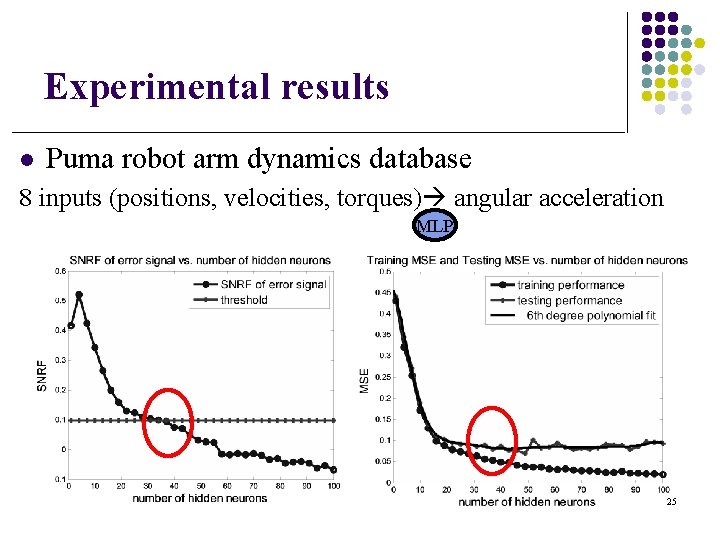
Experimental results l Puma robot arm dynamics database 8 inputs (positions, velocities, torques) angular acceleration MLP 25

Conclusions l l l Quantitative criterion based on SNRF to optimize number of hidden neurons in MLP Detect overfitting by training error only No separate test set required Criterion: simple, easy to apply, efficient and effective Optimization of other parameters of neural networks or fitting problems 26