Optimizing Multipliers for the CPU A ROM based

Optimizing Multipliers for the CPU: A ROM based approach Michael Moeng Jason Wei Electrical Engineering and Computer Science University of California: Berkeley

Problem n Many power-limited applications for CPU ¨ Media/Graphics ¨ Portable n applications Investigating the impact of different multiplier designs on power and performance of CPU: ¨ Simple. Scalar to model CPU and benchmarks ¨ Modify Simple. Scalar multiplier cycle times to model different multiplier architectures

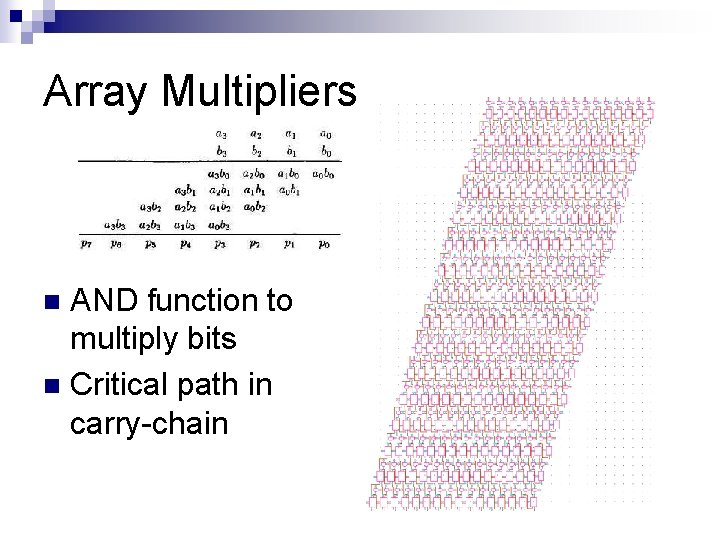
Array Multipliers AND function to multiply bits n Critical path in carry-chain n

Wallace Multipliers Critical path shortened n Final Adder still needed to combine partial products n Power consumption approximately the same as Array Multiplier n

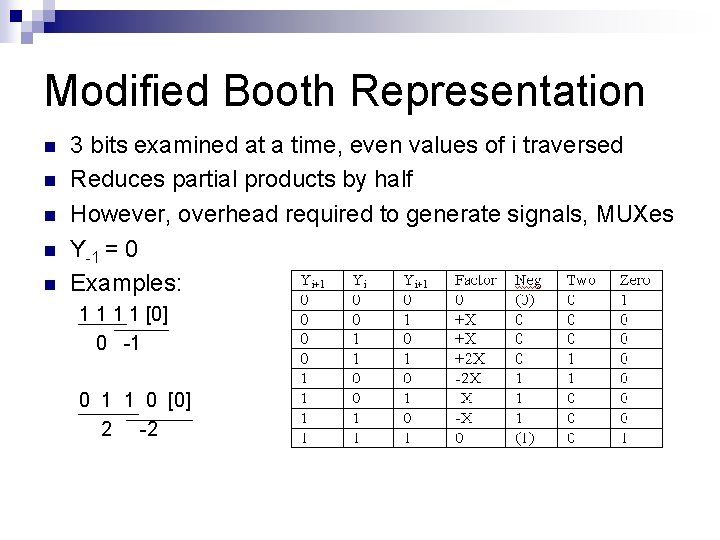
Modified Booth Representation n n 3 bits examined at a time, even values of i traversed Reduces partial products by half However, overhead required to generate signals, MUXes Y-1 = 0 Examples: 1 1 [0] 0 -1 0 1 1 0 [0] 2 -2

Read Only Memory n n Desirable because of low power requirements Con stems from read delay, size 240 MHz -> 4. 2 ns delay Consumes 3. 24 m. W at 100 MHz (10 ns delay)

ROM-based multipliers n ROM-based multipliers attractive ¨ Issue of space n 32 -bit multiplier requires 232*64 bits—unrealistic n Techniques to reduce table sizes ¨ Karatsuba Algorithm: n A=A 31 -16 A 15 -0, B=B 31 -16 B 15 -0 n A*B=A 31 -16 B 31 -16<<32+A 15 -0 B 31 -16<<16+A 31 -16 B 15 -0<<16+A 150 B 15 -0 n n Reduces table size to 216*32 bits, but requires 4 lookups and 3 additions. Using multiple, parallel lookups still uses fewer bits than regular table lookup

ROM-based multipliers cont. ¨ Vinnakota’s approach – Use tables of squares n Let x = floor([A + B]/2) and y = floor([A- B]/2) n If A 0 xor B 0 n n Reduces table size to 232 * 64 bits, further reducible with splittables (introduced later), requires 2 table lookups and 3 (or 4) additions ¨ Hybrid n = 0: A*B = x 2 -y 2 = 1: A*B = x 2 -y 2 +B approach: Use tables of squares to find partial products for Karatsuba algorithm

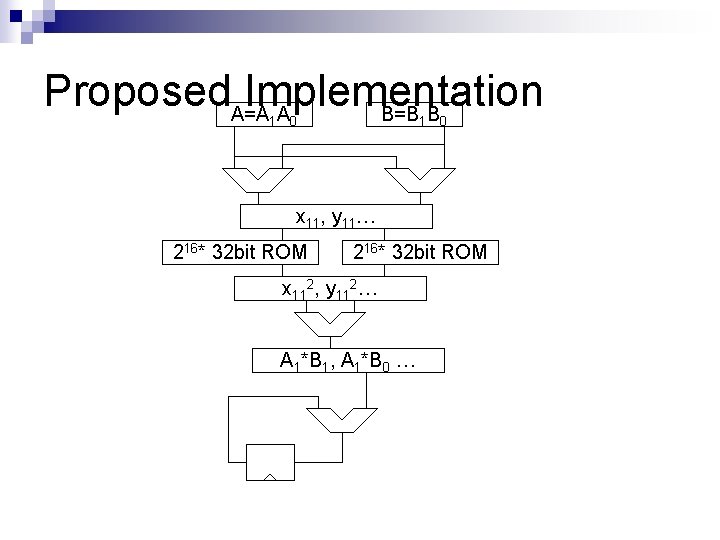
Proposed. A=A Implementation A B=B B 1 0 x 11, y 11… 216* 32 bit ROM x 112, y 112… A 1*B 1, A 1*B 0 …

Results ¨ Most of the SPEC 2000 benchmarks exhibited little or no performance loss (<. 5%) from extra multiplier cycles: art, bzip*, gcc, gzip*, ijpeg, li, mcf, mesa, parser*, vpr ¨ ¨ : Significant * : Possibly significant ¨ Of applications that did experience a drop in performance (extra cycles): n n go. outorder (6. 41%) – go playing program m 88 ksim (5. 39%) – chip simulator perl (0. 72%) – perl interpreter vortex (2. 33%) – Object Orientated Database

Further Work n Measurements: ¨ Accurate power measurements ¨ More specific benchmarks—targeting multimedia n Optimizations: ¨ Tables: n n n Vinnakota’s split-table work If A, B share lower k bits, A 2, B 2 share lower k+1 bits. Can change 2 N*N table to 2 N*(N-[k+1]) and 2 k*(k+1) tables. Gives somewhat faster lookups and lower memory requirements. ¨ Adders: n n Adders can be optimized, final 64 -bit additions are more like 48 -bit additions. Pipelining multiplication operations can occur in up to 3 stages.