Optimizing Group Sequential Designs that Allow Changes to

Optimizing Group Sequential Designs that Allow Changes to the Population Sampled Based on Interim Data Michael Rosenblum Department of Biostatistics Johns Hopkins Bloomberg School of Public Health Joint Work with Mark J. van der Laan Division of Biostatistics University of California, Berkeley

``Death is caused by swallowing small amounts of saliva over a long period of time. ” --George Carlin <<La mort est causé par ingestion de petites quantités de salive sur une longue période de temps. >> --George Carlin

Outline of Talk • Motivation: Why Change the Population Sampled in Group Sequential Designs? • Simple Example • Our Method Applied to Example • Use Results to Compare Power of Adaptive vs. Non-Adaptive Designs

Adaptive Clinical Trial Designs FDA is Interested: “A large effort has been under way at FDA during the past several years to encourage the development and use of new trial designs, including enrichment designs. ”

Adaptive Clinical Trial Designs • Pharmaceutical Companies are Interested: “An adaptive clinical trial conducted by Merck saved the company $70. 8 million compared with what a hypothetical traditionally designed study would have cost…”

Why Use Adaptive Designs? Benefits: – Can Give More Power to Confirm Effective Drugs and Determine Subpopulations who Benefit Most – Can Reduce Cost, Duration, and Number of Subjects of Trials Designs Must: – Control Probability of False Positive Results

Group Sequential Randomized Trial Designs • Participants Enrolled over Time • At Interim Points, Can Change Sampling in Response to Accrued Data.

FDA Draft Guidance on Adaptive Designs Focus is AW&C (adequate and wellcontrolled) trials. Distinguishes well understood vs. less well understood adaptations. Explains chief concerns: Type I error, bias, interpretability.

FDA Draft Guidance on Adaptive Designs Well Understood Adaptations: • Adapt Study Eligibility Criteria Using Only Pre-randomization data. • Adapt to Maintain Study Power Based on Blinded Interim Analyses of Aggregate Data (or Based on Data Unrelated to Outcome). • Adaptations Not Dependent on Within Study, Between-Group Outcome Differences

FDA Draft Guidance on Adaptive Designs Well Understood Adaptations: • Group Sequential Methods (i. e. Early Stopping)

FDA Draft Guidance on Adaptive Designs Less-Well Understood Adaptations: • Adaptive Dose Selection • Response-Adaptive Randomization • Sample Size Adaptation Based on Interim-Effect Size Estimates • Adaptation of Patient Population Based on Treatment-Effect Estimates • Adaptive Endpoint Selection

FDA Draft Guidance on Adaptive Designs Adaptation of Patient Population Based on Treatment-Effect Estimates “These designs are less well understood, pose challenges in avoiding introduction of bias, and generally call for statistical adjustment to avoid increasing the Type I error rate. “

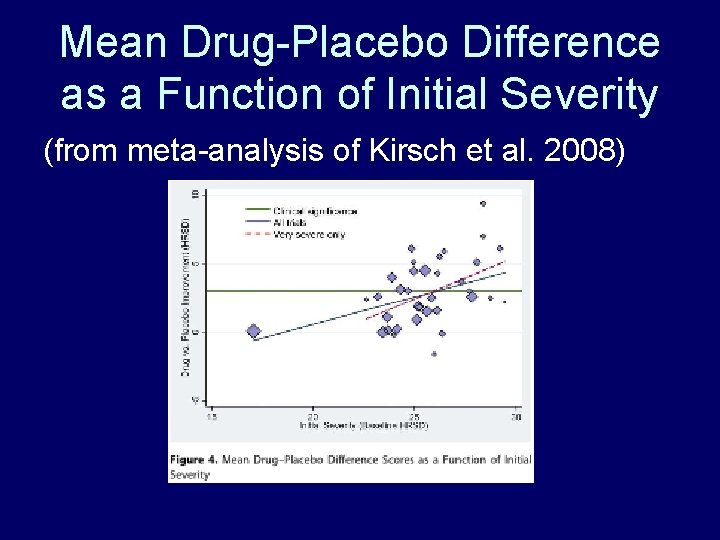
Example Population: Subjects with depression. Research Questions: How does a new antidepressant compare to placebo in effect on change in Hamilton Rating Score of Depression (HRSD) after 6 weeks? Does it differ depending on initial severity of depression? Prior Data Indicates: Maybe only a treatment benefit for those with severe initial depression.

Mean Drug-Placebo Difference as a Function of Initial Severity (from meta-analysis of Kirsch et al. 2008)

Some Possible Fixed Designs • Enroll from total population (both those with moderate initial depression and severe initial depression) Subpopulation 1 Subpopulation 2 • Enroll only from those with severe initial depression Subpopulation 2

Enrichment Design Recruitment Procedure Stage 1 Recruit Both Populations Subpopulation 1 Subpopulation 2 Decision If Treatment Effect Strong in Total Pop. Else, if Treatment Effect Stronger in Subpop. 1 Else, if Treatment Effect Stronger in Subpop. 2 Stage 2 Recruit Both Pop. Subpopulation 1 Subpopulation 2 Recruit Only Subpop. 1 Subpopulation 1 Recruit Only Subpop. 2 Subpopulation 2

Problem and Goals • Problem: Analyze Group Sequential Designs that Allow Changes to Population Sampled at Interim Points, Based on Earlier Data (Including Outcomes Data) • Goals: 1. Make Inferences about Selected Populations 2. Control Asymptotic, Worst-case, Familywise Type I Error Rate, Making No Model Assumptions • Our Contribution: General Method for Reducing Problem to Optimization Problem that Can Be Easy to Solve with Standard Statistical Software

Some Related Work • Adapt Treatments and/or Population Sampled [Thall, Simon, Ellenberg 1988, Schaid, Wieand, Therneau 1990, Wittes and Brittain 1990, Follman 1997, Bauer and Köhne 1994, Bauer and Kieser 1999, Liu, Proschan, Pledger 2002, Stallard and Todd 2003, Sampson and Sill 2005, Bischoff and Miller 2005, Freidlin and Simon 2005, Jennison and Turnbull, 2003, 2006, 2007, Wang, Hung, O’Neill 2009]

Our Contribution Theorem that Gives Reduction of Problem of Computing Asymptotic, Worst-Case, Familywise Error Rate to Optimization Problem that Often Can be Solved Numerically with Standard Statistical Software. Reduces Problem to Computations of Probability that a Multivariate Normal is in a Set of Regions (that Depend on Design).

Scope of Method • • Can be applied to studies with: Any number of pre-planned treatment arms Any number of pre-planned stages Sequential testing Adaptation of Randomization Probabilities

Asymptotic, Worst-case familywise Type I Error • We get sharp bounds on the asymptotic, worst-case, Type I error. • For sample size n, P’ the set of possible data generating distributions, this is defined as:

Example from Earlier • 2 -Stage Design, 2 Subpopulations of Interest • Three Null Hypotheses: H 00: Mean Effect in Total (Mixture) Population is ≤ 0. H 01: Mean Effect in Subpopulation 1 (moderate) is ≤ 0. H 02: Mean Effect in Subpopulation 2 (severe) is ≤ 0. • Stage 1: Recruit Equal Number of Subjects from Each Subpopulation. Get t-statistics: • Stage 2: if recruit as in Stage 1. Else, Recruit from severe depressed only. • Test Procedure: if then reject null for the population enrolled in stage 2. • Our Method Shows Asympt. Worst Case, FWER ≤ 0. 05.

Computation of Worst-Case Asymptotic Familywise Error Rate Consider Case of μ 1 > 0 (H 01 false), and μ 2 = 0 (H 02 true). Type I Error only when Subpopulation 2 Selected for Recruitment in Stage 2, AND Final Statistic: By our Theorem, we have uniformly* in μ 1 , σ1, σ2:

Computation of Worst-Case Asymptotic Familywise Error Rate Worst-Case Familywise Error Rate for case: μ 1 > 0 (H 01 false), and μ 2 = 0 (H 02 true) Thus, in the Case: μ 1 > 0 (H 01 false), and μ 2 = 0 (H 02 true), we have Asymptotic, Worst-Case, FWER at most

Computation of Worst-Case Asymptotic Familywise Error Rate More generally, for more complex designs, need to solve optimization problems of the form: where X is a multivariate normal random variable with mean vector and covariance matrix that are functions of. , for R and S fixed regions. Solve by grid search combined with bound on approximation error of grid search.

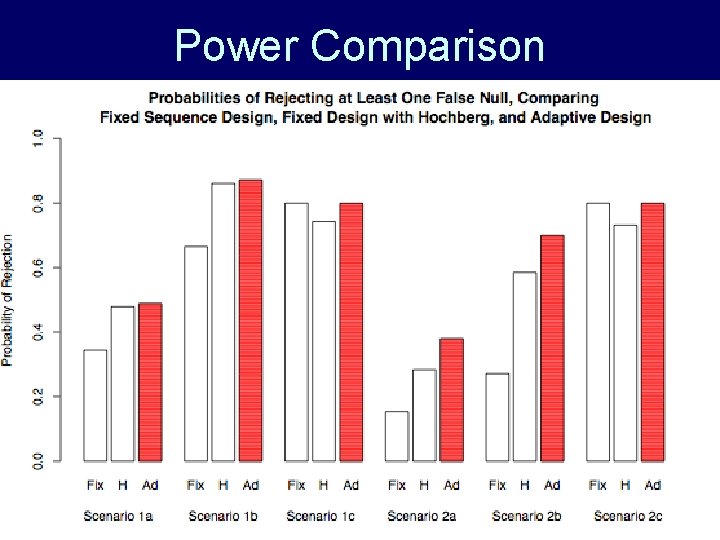
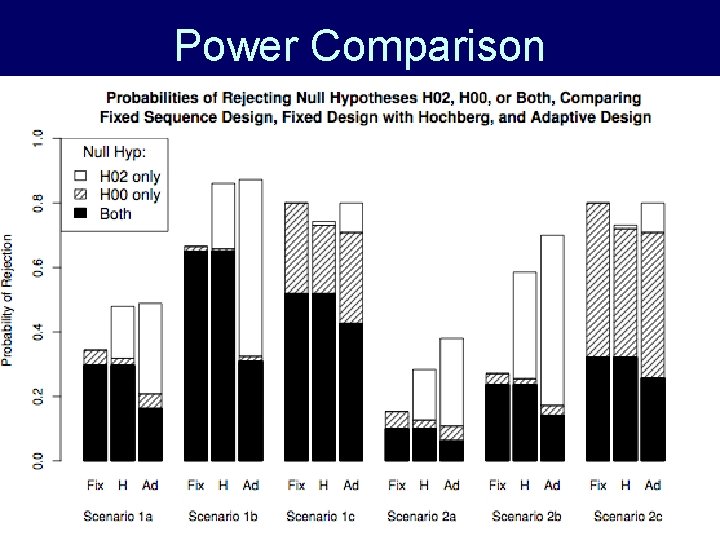
Power Comparison Consider 3 scenarios: a) New antidepressant works only for those with severe initial depression, and mean benefit modest (1. 8 HRSD points) b) Same as (a) but benefit strong (3 pts. ) c) New antidepressant works equally well for those with moderate and with severe initial depression, and benefit modest. For each, consider: 1. first stage enrolls equally from each subpop 2. 75% of first stage enrolled moderate depr.

Power Comparison

Power Comparison

When Our Method Can Be Applied Our Main Theorem: • Gives Reduction of Problem of Computing Worst-Case, Asymptotic Familywise Error Rate to Optimization Problem that Often Can be Solved with Standard Statistical Software • Relies on: 1. Prespecification of Adaptation Algorithm 2. Centered Statistics from Each Stage Asymptotically Normal, and Independent of Past Stage Data Given Previous Design Decision. 3. Uniform Convergence in (2). 4. Selection and Rejection Regions Simple to Compute.

Assumptions To Get Uniform Asymptotic Normality of Test Statistics, Conditioned on Prior Design Selection, Need to Assume: • Variances Bounded Away from Zero • Sample Size at Each Stage Goes to Infinity To Efficiently Compute Asymptotic FWER: • Decision Regions for Between-Stage Adaptations and Rejection Regions Easy to Specify and Compute. • Asymptotic Distribution of Test Statistics Depends on Finite Dimensional Parameter of Data Generating Distribution (e. g. Moments)

Limitations of Adaptation • In General No Guarantee of Power Gain; May Lead to Loss of Efficiency • Enrichment Designs Result in Reduced Generalizability of Results • May Encourage Poorly Planned Designs (with Hope Adaptation will Fix Everything)

Open Problems Generalizing Our Method to Designs with: • Adaptation of Monitoring Frequency • Adaptation of List of Covariates Collected • Survival Outcomes Confidence Intervals

Conclusions General Method for Reducing Problem of Computing Worst-case, Asymptotic, Familywise Error Rate to Optimization Problem that Often Can Be Easy to Solve with Standard Statistical Software.

References Rosenblum, M. and van der Laan, M. J. Optimizing Randomized Trial Designs to Distinguish which Subpopulations Benefit from Treatment (under review) http: //people. csail. mit. edu/mrosenblum/adaptive_subpop. pdf Kirsch, I. , Deacon, B. , Huedo-Medina, T. , Scoboria, A. , Moore, T. & et al. (2008). Initial severity and antidepressant benefits: A metaanalysis of data submitted to the food and drug administration. PLo. S Med 5, e 45. doi: 10. 1371/journal. pmed. 0050045. FDA (2010). Draft Guidance for Industry. Adaptive Design Clinical Trials for Drugs and Biologics. http: //www. fda. gov/downloads/Drugs/Guidance. Compliance. Regulato ry. Information/Guidances/UCM 201790. pdf

Comparison to Alternative Analysis Method based on [Bauer and Köhne 1994]: Use Closed Test Principle [Marcus 1976] to Deal with Multiple Hypotheses, and Prespecified Function to Combine Stagewise p-values. • Extremely Useful, Flexible Method • Facilitates Proving Bounds on FWER • Restricted to Cases where p-values in Each Stage Dominate U[0, 1] under Intersection Null Hypotheses.

Group Sequential Designs We Consider • K stages (though may stop early) • Population Sampled at Stage m is Prespecified Function of Data Collected in Past Stages. • Allow Early Stopping for Efficacy, Safety, or Futility • Prespecify: Primary Outcome, Null Hypotheses, Test statistics, Rejection Regions

When Our Method Can Be Applied Our Main Theorem: • Gives Reduction of Problem of Computing Worst-Case, Asymptotic Familywise Error Rate to Optimization Problem that Often Can be Solved with Standard Statistical Software • Relies on: 1. Prespecification of Adaptation Algorithm 2. For Each Possible Design Selection Before a Stage, Resulting Centered Test-Statistics from that Stage Asymptotically Normal (e. g. t-test or log-rank test) 3. Uniform Convergence in (2). 4. Selection and Rejection Regions Simple to Compute.