Optimizing Expected Time Utility in CyberPhysical Systems Schedulers

Optimizing Expected Time Utility in Cyber-Physical Systems Schedulers Terry Tidwell, Robert Glaubius, Christopher Gill, William Smart Washington University in St. Louis 6/8/2021 RTSS 2010 1

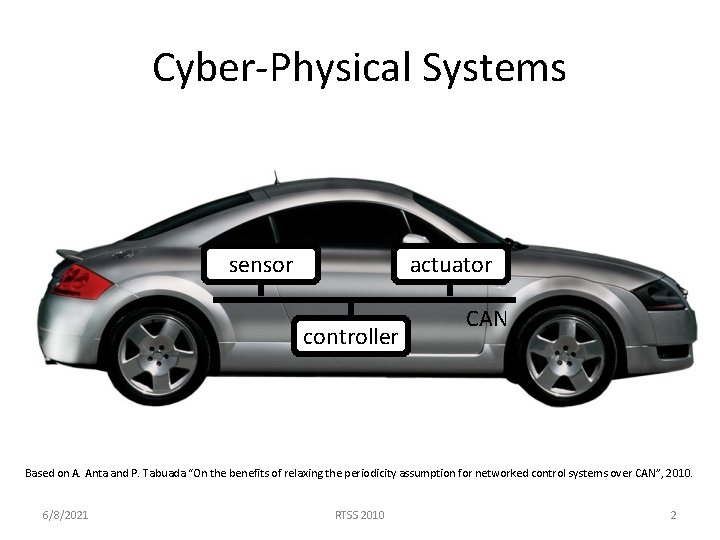
Cyber-Physical Systems sensor actuator controller CAN Based on A. Anta and P. Tabuada “On the benefits of relaxing the periodicity assumption for networked control systems over CAN”, 2010. 6/8/2021 RTSS 2010 2

Cyber-Physical Systems sensor actuator Problem: Current real-time scheduling CAN abstractions are insufficient controller Based on A. Anta and P. Tabuada “On the benefits of relaxing the periodicity assumption for networked control systems over CAN”, 2010. 6/8/2021 RTSS 2010 3

Periodic Real-Time Task • Periodic Tasks [Lui&Layland 73] – Series of jobs – Release time, deadlines, worst case execution time – Basic scheduling goal: minimizing deadline miss rate 0 6/8/2021 p 2 p RTSS 2010 3 p Time 4

Periodic Real-Time Task • Periodic Tasks [Lui&Layland 73] – Series of jobs – Release time, deadlines, worst case execution time – Basic scheduling goal: minimizing deadline miss rate Problem: Deadline and worst case execution time only bounds behavior 0 6/8/2021 p 2 p RTSS 2010 3 p Time 5

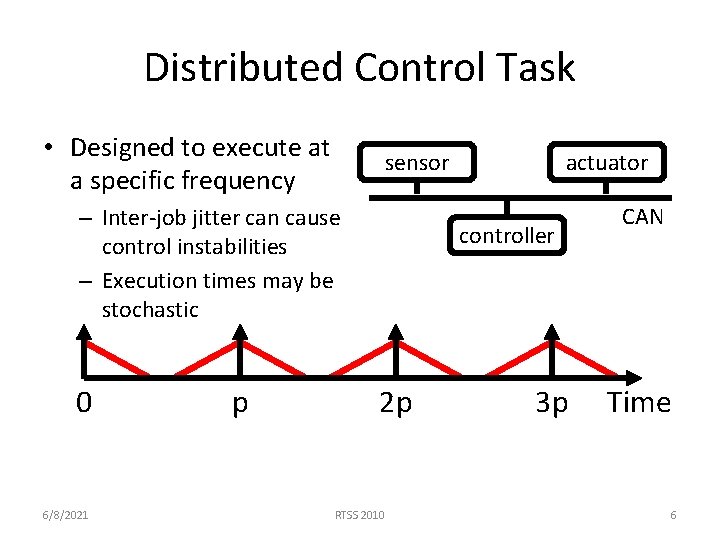
Distributed Control Task • Designed to execute at a specific frequency sensor – Inter-job jitter can cause control instabilities – Execution times may be stochastic 0 6/8/2021 p actuator controller 2 p RTSS 2010 3 p CAN Time 6

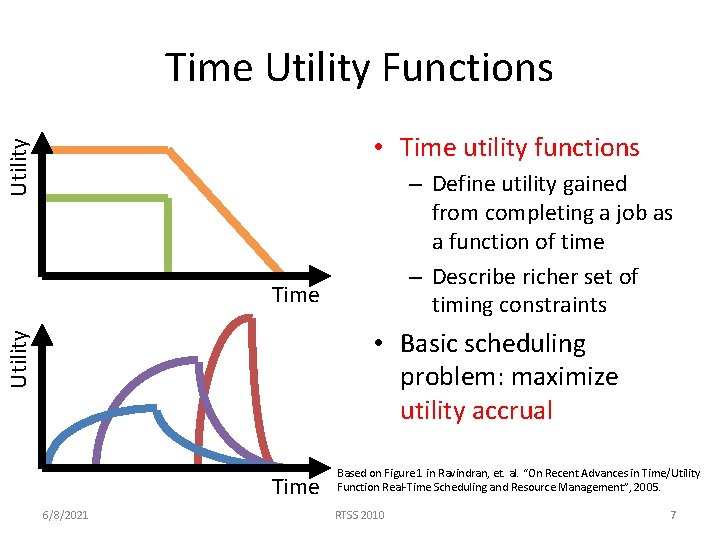
Time Utility Functions Utility • Time utility functions – Define utility gained from completing a job as a function of time – Describe richer set of timing constraints Time Utility • Basic scheduling problem: maximize utility accrual Time 6/8/2021 Based on Figure 1 in Ravindran, et. al. “On Recent Advances in Time/Utility Function Real-Time Scheduling and Resource Management”, 2005. RTSS 2010 7

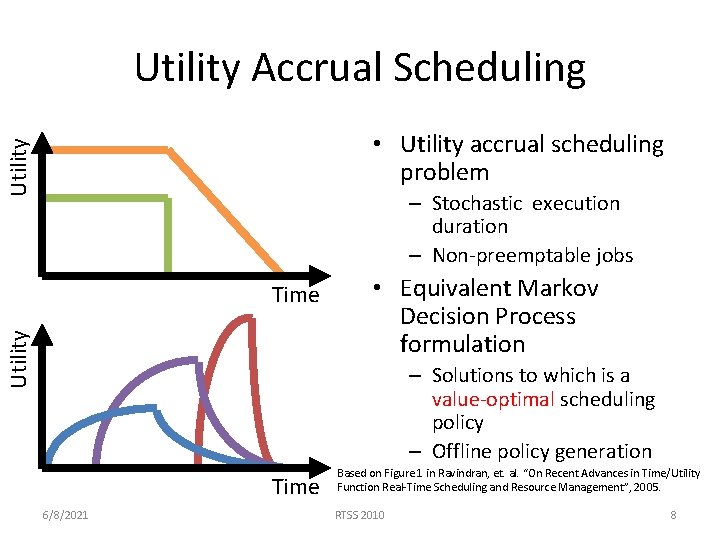
Utility Accrual Scheduling Utility • Utility accrual scheduling problem – Stochastic execution duration – Non-preemptable jobs Utility Time • Equivalent Markov Decision Process formulation – Solutions to which is a value-optimal scheduling policy – Offline policy generation Time 6/8/2021 Based on Figure 1 in Ravindran, et. al. “On Recent Advances in Time/Utility Function Real-Time Scheduling and Resource Management”, 2005. RTSS 2010 8

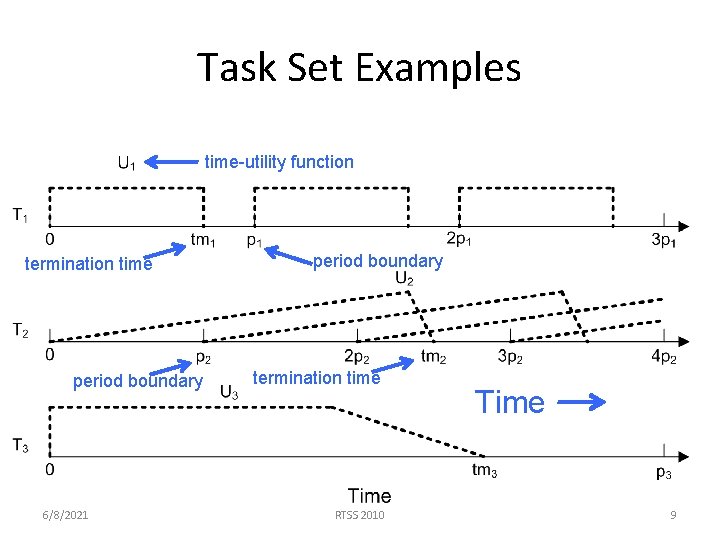
Task Set Examples time-utility function termination time period boundary 6/8/2021 period boundary termination time RTSS 2010 Time 9

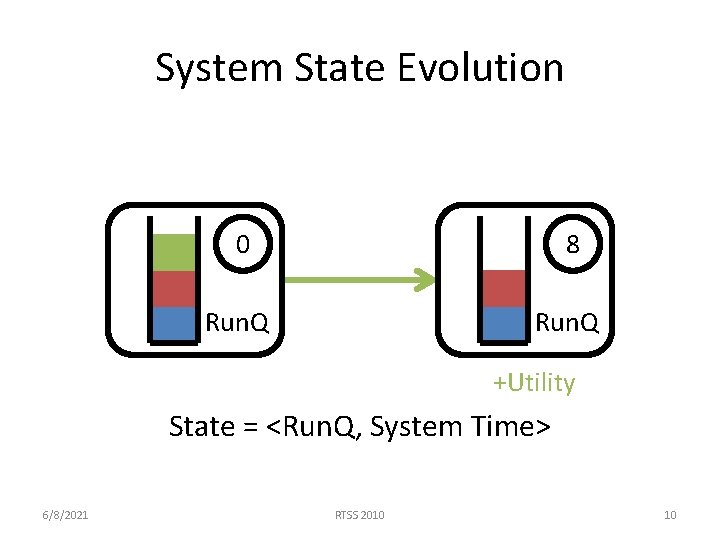
System State Evolution 0 8 Run. Q +Utility State = <Run. Q, System Time> 6/8/2021 RTSS 2010 10

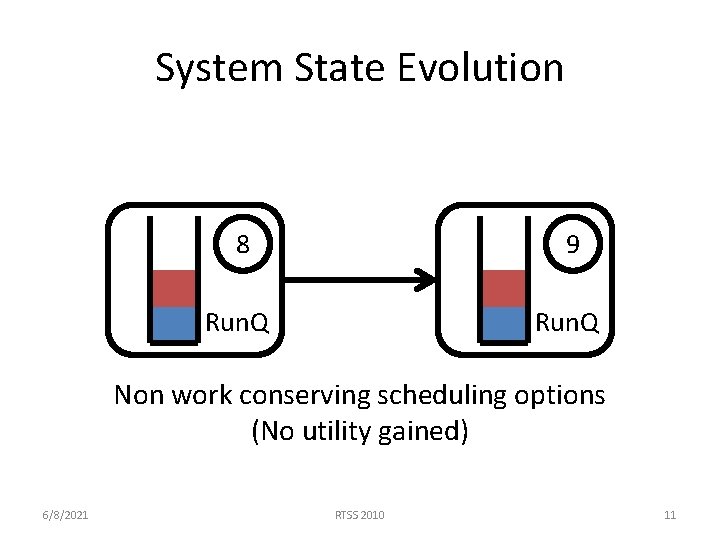
System State Evolution 8 9 Run. Q Non work conserving scheduling options (No utility gained) 6/8/2021 RTSS 2010 11

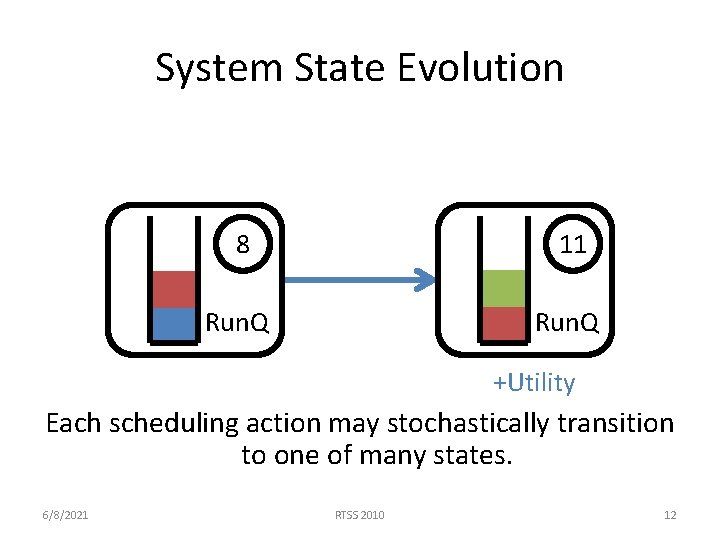
System State Evolution 8 11 Run. Q +Utility Each scheduling action may stochastically transition to one of many states. 6/8/2021 RTSS 2010 12

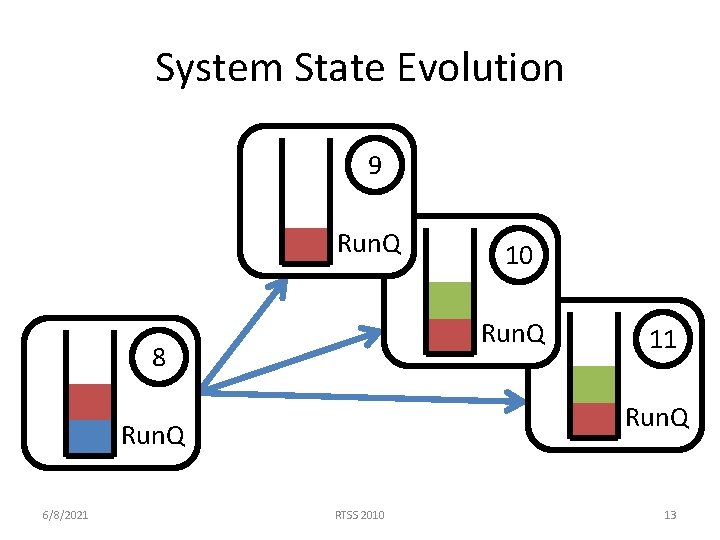
System State Evolution 9 Run. Q 8 11 Run. Q 6/8/2021 10 RTSS 2010 13

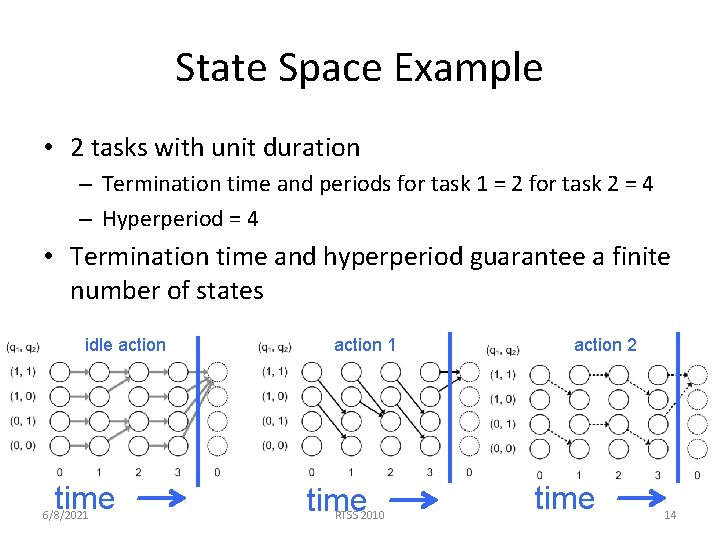
State Space Example • 2 tasks with unit duration – Termination time and periods for task 1 = 2 for task 2 = 4 – Hyperperiod = 4 • Termination time and hyperperiod guarantee a finite number of states idle action time 6/8/2021 action 1 time RTSS 2010 action 2 time 14

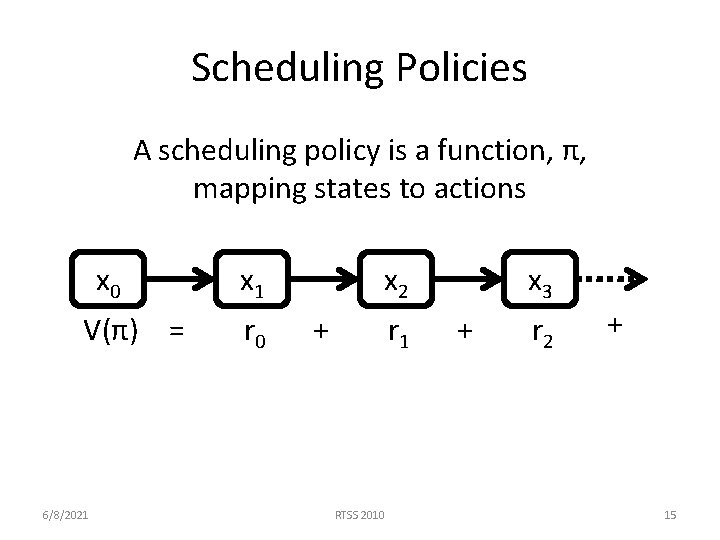
Scheduling Policies A scheduling policy is a function, π, mapping states to actions x 0 V(π) = 6/8/2021 x 1 r 0 x 2 + r 1 RTSS 2010 x 3 + r 2 + 15

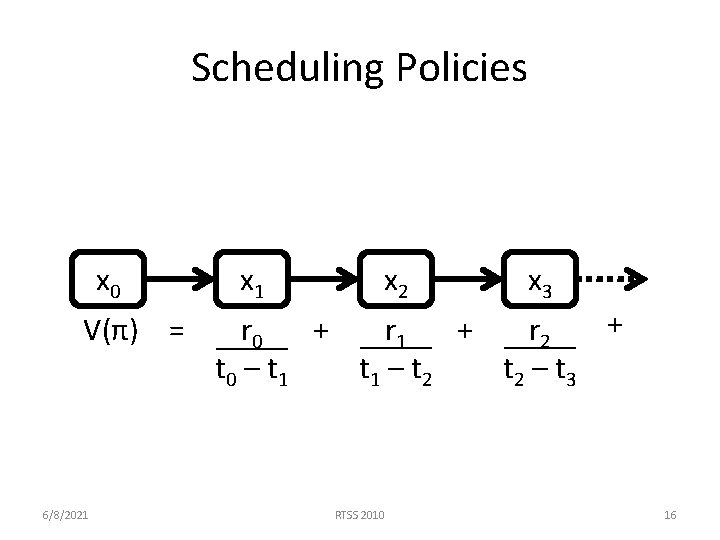
Scheduling Policies x 0 V(π) = 6/8/2021 x 2 x 3 + r 0 + r 1 + r 2 t 0 – t 1 – t 2 – t 3 RTSS 2010 16

Scheduling Policies 0≤γ≤ 1 x 0 x 1 V(π) = x 2 x 3 γ 0 r 0 + γ 1 r 1 + γ 2 r 2 + t 0 – t 1 – t 2 – t 3 V(π) is the value of the policy 6/8/2021 RTSS 2010 17

Scheduling Policies 0≤γ≤ 1 x 0 Existingxtechniques x 2 can generate x 3 1 scheduling + V(π) = γ 0 policies r + that γ 1 r optimize + γ 2 value r 0 t 0 – t 1 1 t 1 – t 2 2 t 2 – t 3 V(π) is the value of the policy 6/8/2021 RTSS 2010 18

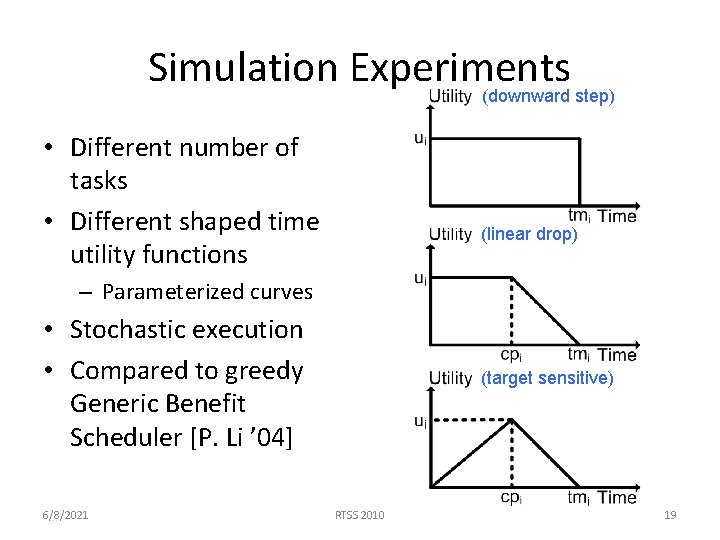
Simulation Experiments (downward step) • Different number of tasks • Different shaped time utility functions (linear drop) – Parameterized curves • Stochastic execution • Compared to greedy Generic Benefit Scheduler [P. Li ’ 04] 6/8/2021 (target sensitive) RTSS 2010 19

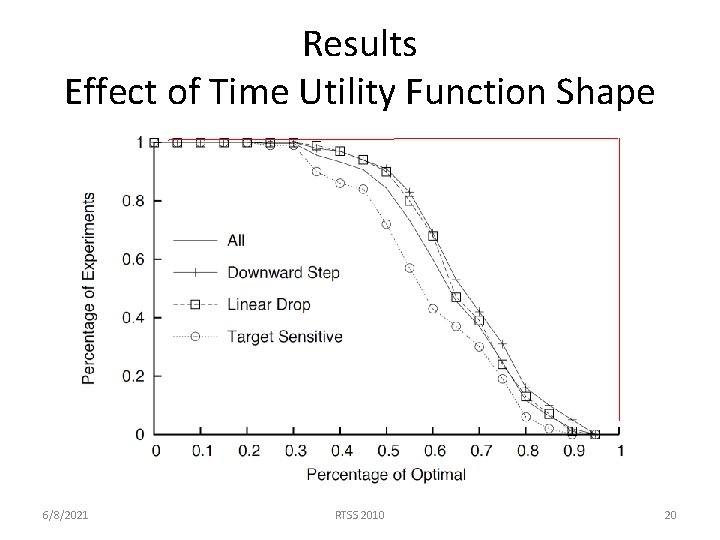
Results Effect of Time Utility Function Shape 6/8/2021 RTSS 2010 20

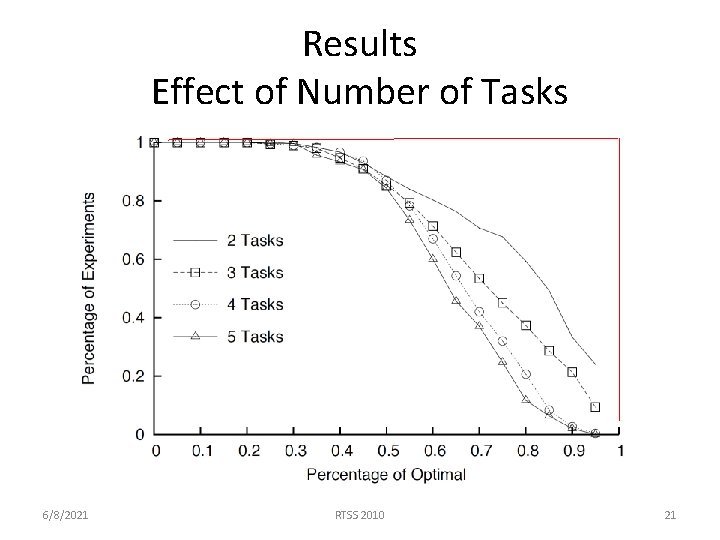
Results Effect of Number of Tasks 6/8/2021 RTSS 2010 21

Conclusions • Real-time scheduling abstractions like deadlines and worst case execution time may not cover all cyber-physical systems • Scheduling policies needed for systems with time utility functions and stochastic execution • Markov Decision Process formulation can give value-optimal utility accrual scheduling policies 6/8/2021 RTSS 2010 22