Optimizing Database Algorithms for RandomAccess Block Devices Risi

Optimizing Database Algorithms for Random-Access Block Devices Risi Thonangi Ph. D Defense Talk Advisor: Jun Yang

Background: Hard-Disk Drives • Hard Disk Drives (HDDs) • Magnetic platters for storage • Mechanical moving parts for data access • I/O characteristics • Fast sequential access & slow random access • Read/write symmetry • Disadvantages • Slow random access • High energy costs • Bad shock absorption 2

Background: Newer Storage Technologies • Flash memory, phase-change memory, ferroelectric RAM and MRAM • Solves HDD’s disadvantages of high energy usage, bad shock absorption, etc. • Representative: flash memory USB Flash Drive • Floating-gate transistors for storage • Electronic circuits for data access • I/O Characteristics – fast random access & Expensive writes • Other technologies (phase-change memory, etc. ) exhibit similar advantages and I/O characteristics 3

Random-Access Block Devices • Devices that are • Block based • Support fast random access but have costlier writes • Popular example – Solid-State Drives (SSDs) • Use flash memory for storage • Have advantages of flash memory • Quickly replacing HDDs in consumer & enterprise storage • Other examples • Cloud storage & key-value store based storage • Phase-change memory 4

Motivation & Problem Statement • Can’t we use random-access block device as a drop-in replacement for HDD? • They do lead to better performance • But can be suboptimal because existing algorithms are not optimized for them Problem statement : – Optimize database algorithms for I/O characteristics of random-access & read/write asymmetry 5

Related work For SSDs • Indexes • BFTL, Flash. DB, LA-tree, FD-tree, etc. • Query processing techniques • PAX style storage & Flash. Join, B-File for maintaining samples • Transaction processing • In-Page Logging, Log-structured storage & optimistic concurrency control, etc. ⇒ We propose new techniques & algorithms that systematically exploit both random access and read/write asymmetry 6

Outline • Permutation problem • Merge policies for Log-Structured Merge (LSM) tree • Concurrency control in indexes • Conclusion & future work [VLDB 2013] “Permuting Data on Random-Access Block Storage”. Risi Thonangi, Jun Yang [Techreport 2015] “Optimizing LSM-tree for Random- Access Block Storage”. Risi Thonangi, Jun Yang [CIKM 2012] “A Practical Concurrent Index for Solid-State Drives”. Risi Thonangi, Shivnath Babu, Jun Yang 7

Permutation problem • 8

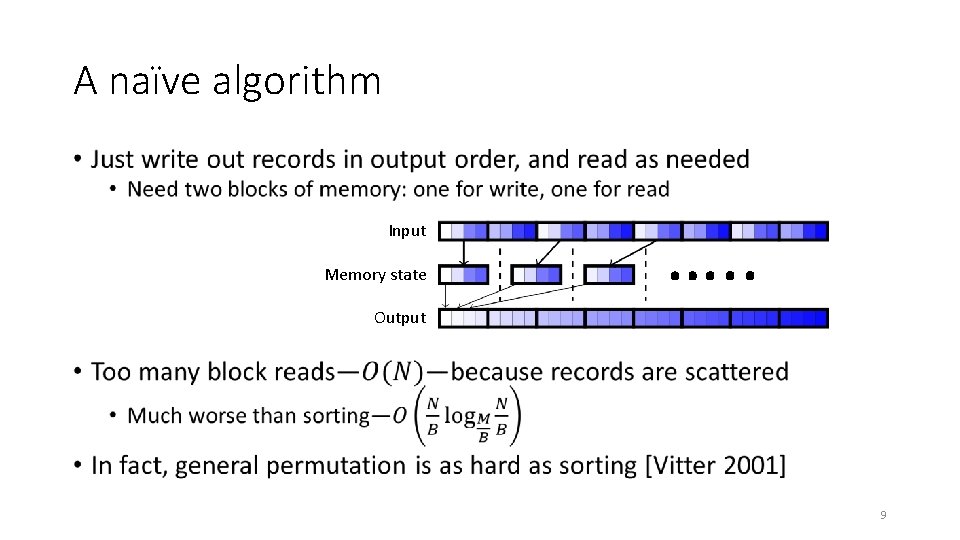
A naïve algorithm • Input Memory state …. . Output 9

Address space • 3 -digit addresses 0 0 0 1 1 1 0 0 0 1 1 1 2 2 2 3 3 3 0 1 2 0 1 2 records 10

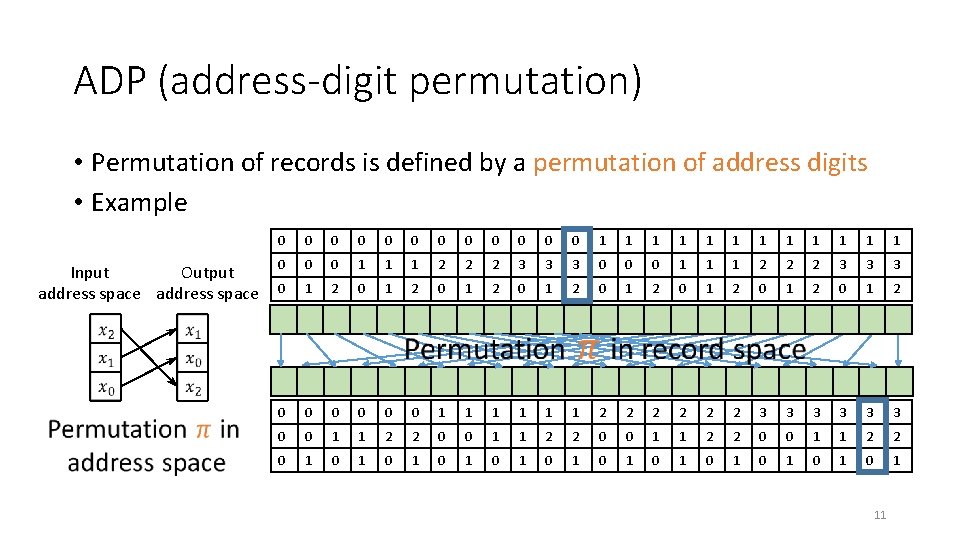
ADP (address-digit permutation) • Permutation of records is defined by a permutation of address digits • Example Output Input address space 0 0 0 1 1 1 0 0 0 1 1 1 2 2 2 3 3 3 0 1 2 0 1 2 0 0 0 1 1 1 2 2 2 3 3 3 0 0 1 1 2 2 0 1 0 1 0 1 11

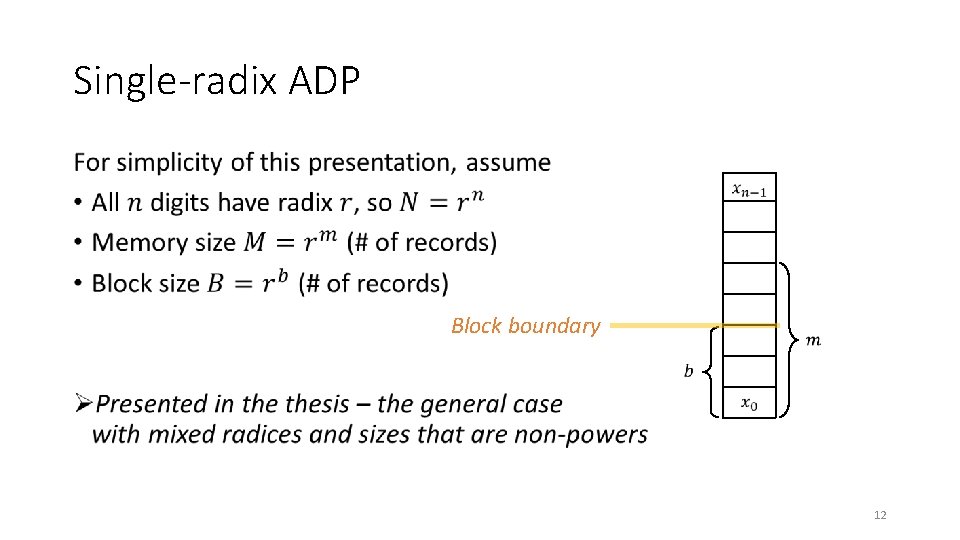
Single-radix ADP • Block boundary 12

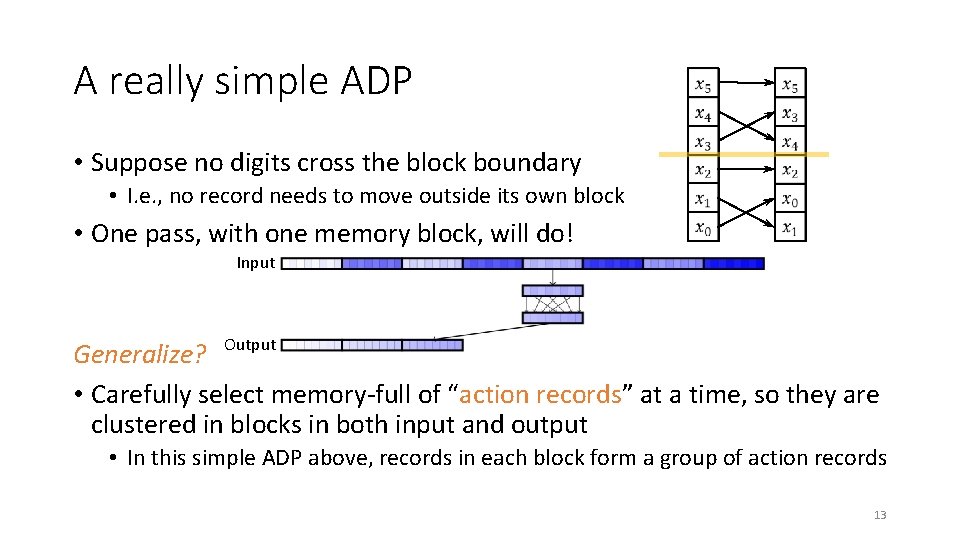
A really simple ADP • Suppose no digits cross the block boundary • I. e. , no record needs to move outside its own block • One pass, with one memory block, will do! Input Generalize? Output • Carefully select memory-full of “action records” at a time, so they are clustered in blocks in both input and output • In this simple ADP above, records in each block form a group of action records 13

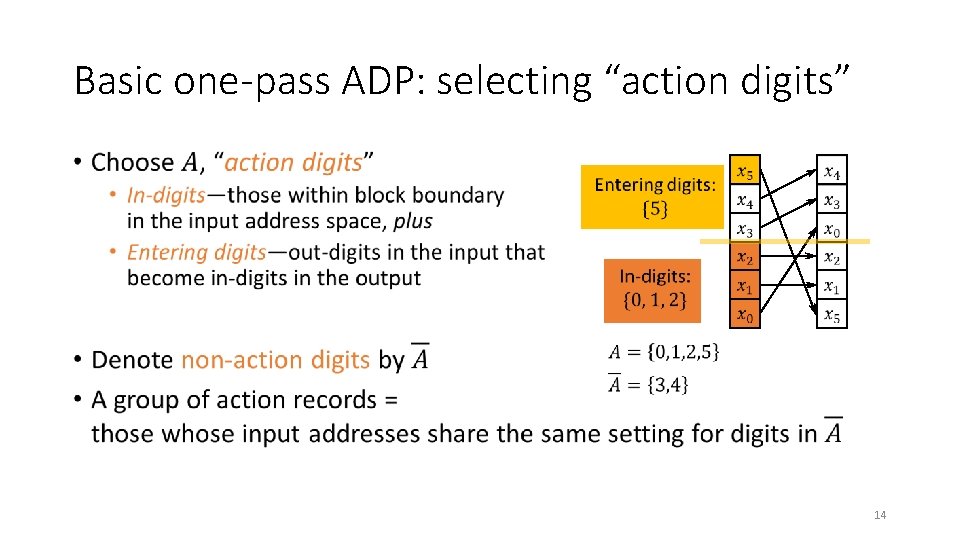
Basic one-pass ADP: selecting “action digits” • 14

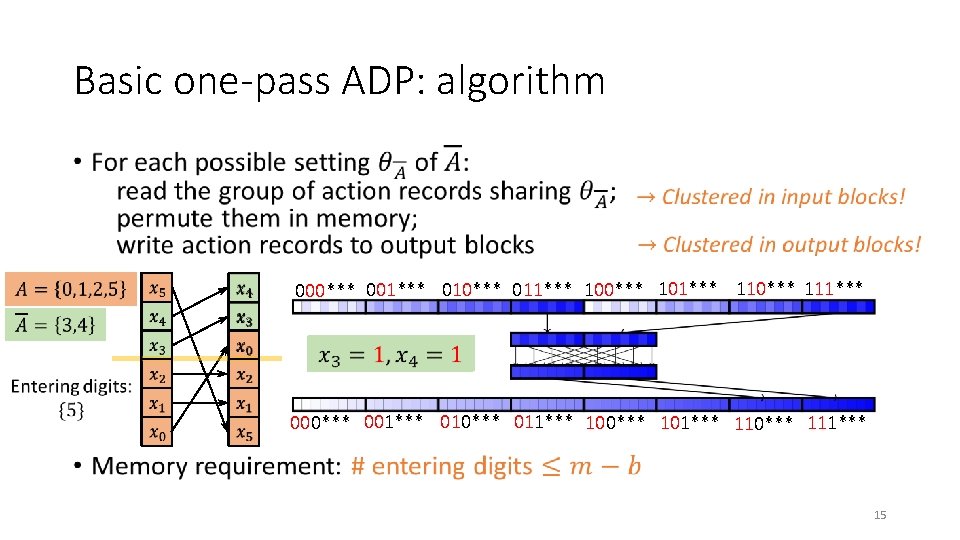
Basic one-pass ADP: algorithm • 000*** 001*** 010*** 011*** 100*** 101*** 110*** 111*** 15

More entering digits than we can handle? • Exploit the read/write asymmetry • Filtered reads: allow a block to be read multiple times in one “pass” • Use multiple passes • Perform a series of simpler permutations whose composition is the desired composition • A cost-based optimizer to determine the passes: ØPresented in thesis – a provably optimal algorithm … which “balances” aggressiveness of filtered reads across passes 16

Permuting vs. sorting for ADP • 17

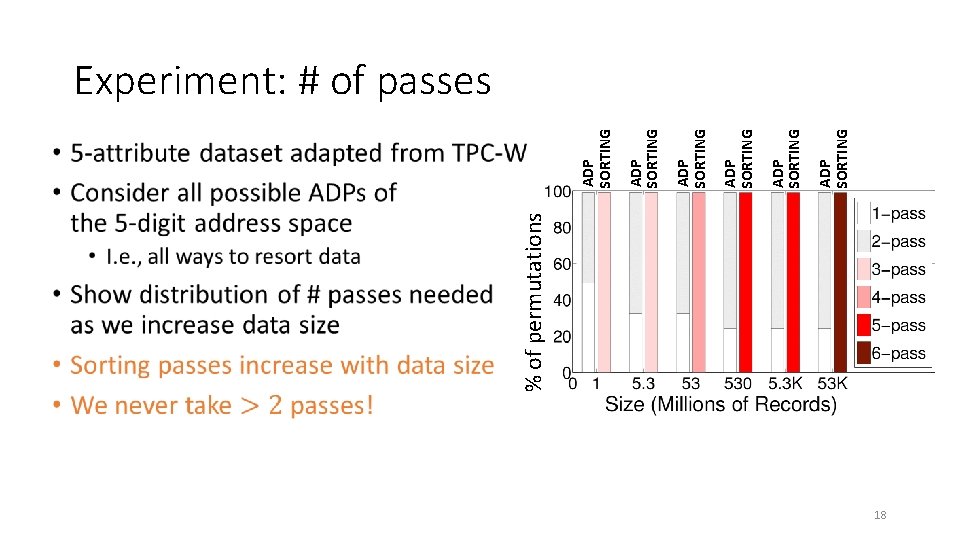
% of permutations • ADP SORTING ADP SORTING Experiment: # of passes 18

Conclusion • Introduced address-digit permutations (ADPs) • Capturing many useful data reorganization tasks • Designed algorithms for ADPs on random-access block storage • Exploiting fast random accesses, read/write asymmetry • Beating sort! • Results not covered in this talk • Optimizations that read/write larger runs of blocks • Mixed radices, memory/blocks sizes that are non-powers of the radices • More experiments, including permuting data stored on SSDs & Amazon S 3 19

Outline • Permutation problem • Merge policies for Log-Structured Merge (LSM) tree • Concurrency control in indexes • Conclusion & future work [VLDB 2013] “Permuting Data on Random-Access Block Storage”. Risi Thonangi, Jun Yang [Techreport 2015] “Optimizing LSM-tree for Random- Access Block Storage”. Risi Thonangi, Jun Yang [CIKM 2012] “A Practical Concurrent Index for Solid-State Drives”. Risi Thonangi, Shivnath Babu, Jun Yang 20

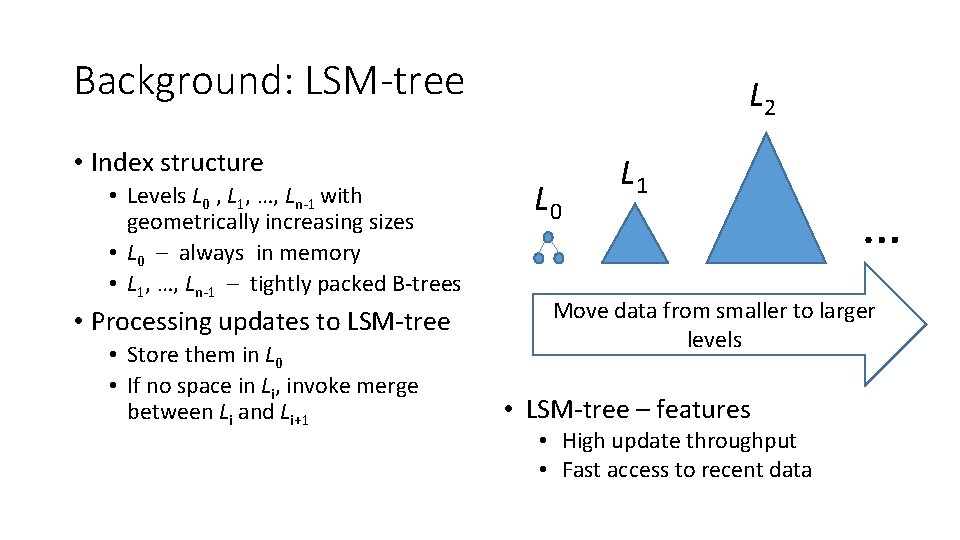
Background: LSM-tree • Index structure • Levels L 0 , L 1, …, Ln-1 with geometrically increasing sizes • L 0 – always in memory • L 1, …, Ln-1 – tightly packed B-trees • Processing updates to LSM-tree • Store them in L 0 • If no space in Li, invoke merge between Li and Li+1 L 2 L 0 L 1 … Move data from smaller to larger levels • LSM-tree – features • High update throughput • Fast access to recent data

Motivation • Existing LSM-tree implementations optimize for HDDs • Minimize random access • Variants are also popular for SSDs, as LSM-tree avoids in-place updates Can we do better? • Optimize LSM-tree for random-access block devices • Minimize writes • Understand improve merge policies

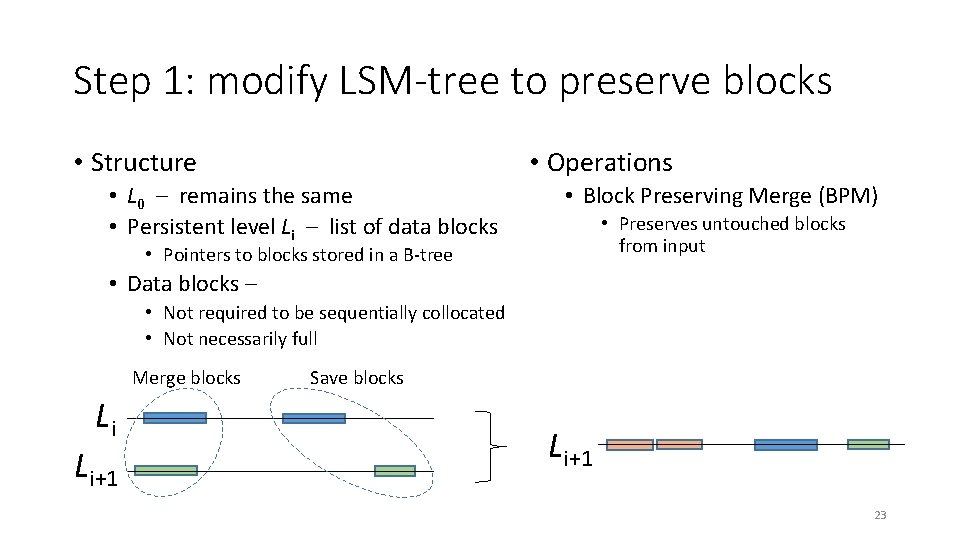
Step 1: modify LSM-tree to preserve blocks • Structure • Operations • L 0 – remains the same • Persistent level Li – list of data blocks • Block Preserving Merge (BPM) • Preserves untouched blocks from input • Pointers to blocks stored in a B-tree • Data blocks – • Not required to be sequentially collocated • Not necessarily full Merge blocks Li Li+1 Save blocks Li+1 23

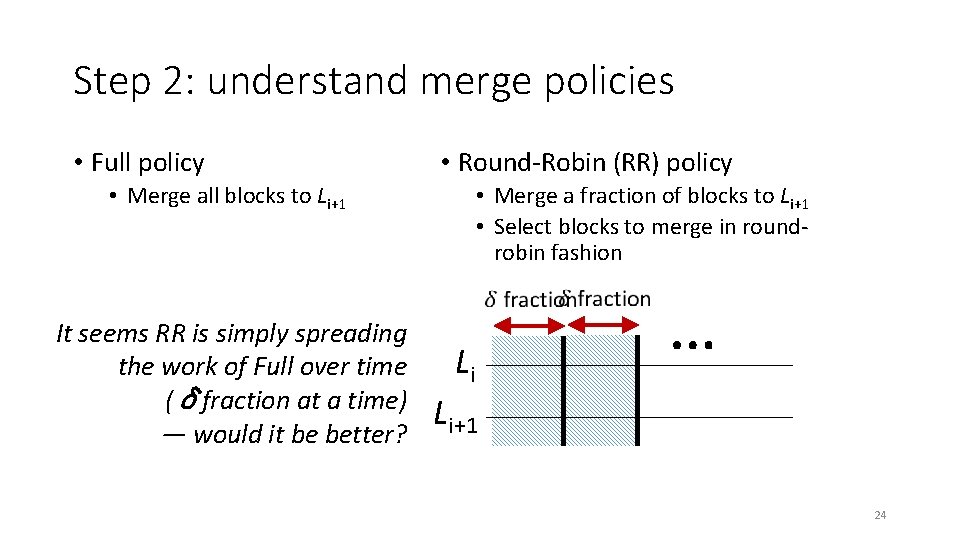
Step 2: understand merge policies • Full policy • Round-Robin (RR) policy • Merge a fraction of blocks to Li+1 • Select blocks to merge in roundrobin fashion • Merge all blocks to Li+1 It seems RR is simply spreading the work of Full over time (δfraction at a time) — would it be better? Li … Li+1 24

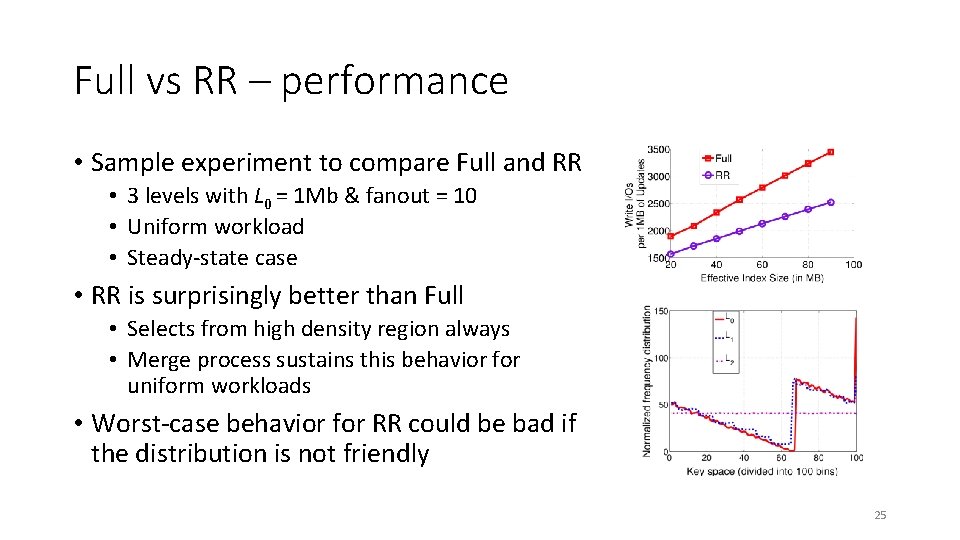
Full vs RR – performance • Sample experiment to compare Full and RR • 3 levels with L 0 = 1 Mb & fanout = 10 • Uniform workload • Steady-state case • RR is surprisingly better than Full • Selects from high density region always • Merge process sustains this behavior for uniform workloads • Worst-case behavior for RR could be bad if the distribution is not friendly 25

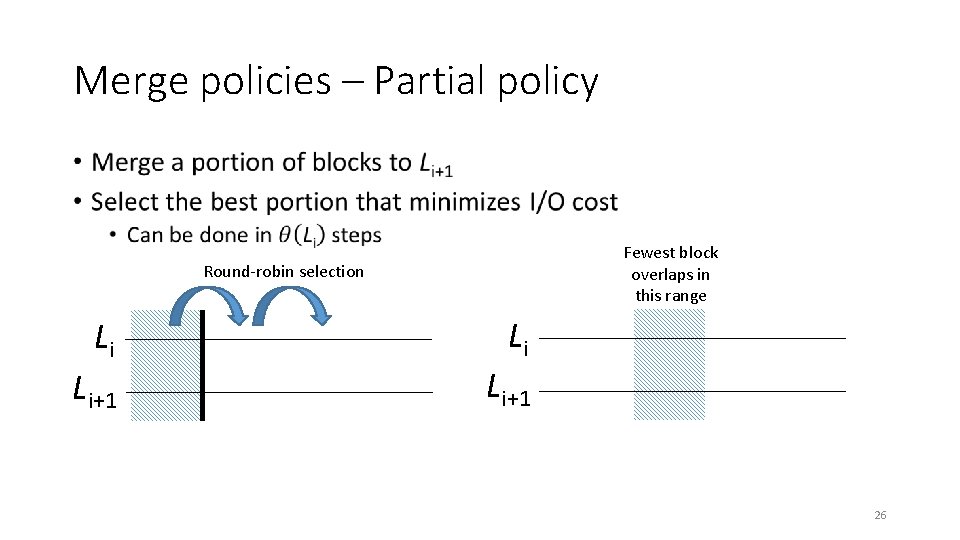
Merge policies – Partial policy • Fewest block overlaps in this range Round-robin selection Li Li+1 26

Partial’s performance guarantee •

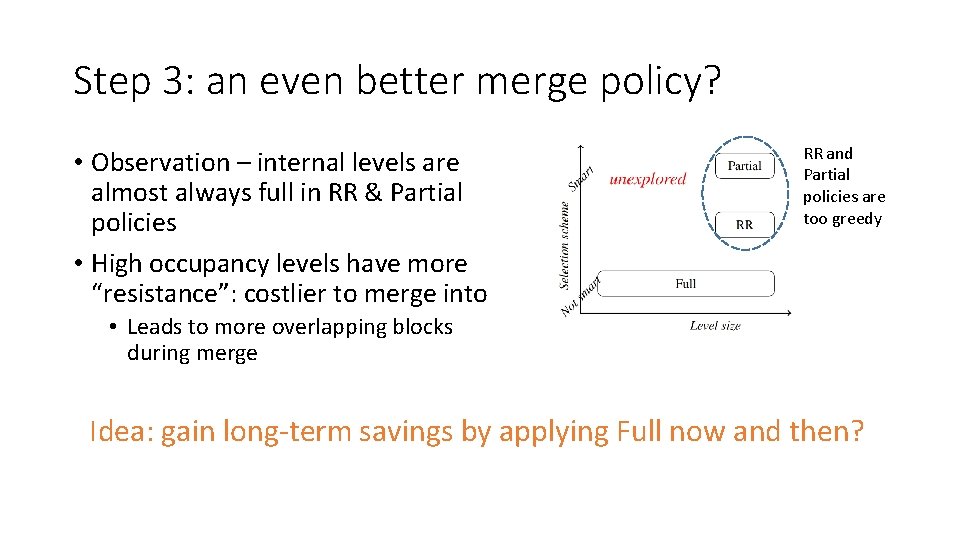
Step 3: an even better merge policy? • Observation – internal levels are almost always full in RR & Partial policies • High occupancy levels have more “resistance”: costlier to merge into RR and Partial policies are too greedy • Leads to more overlapping blocks during merge Idea: gain long-term savings by applying Full now and then?

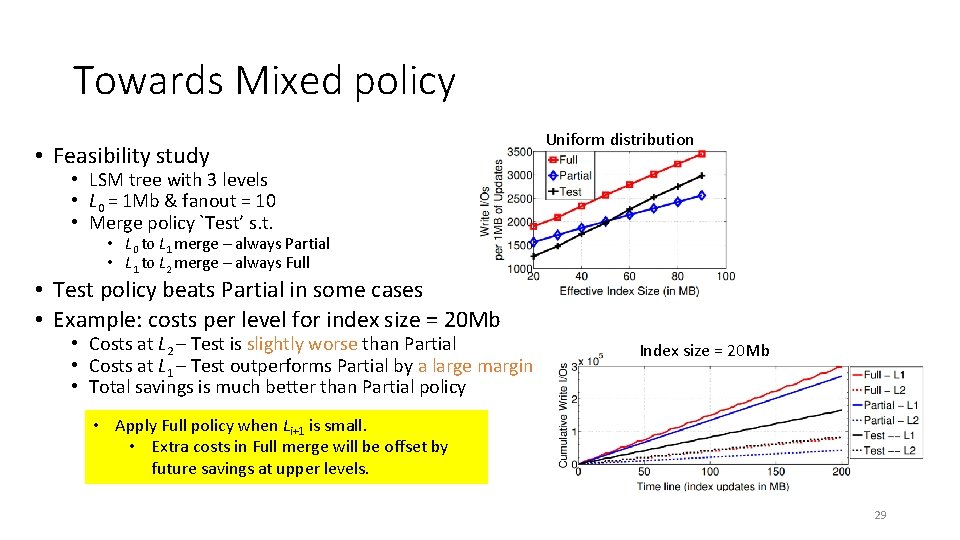
Towards Mixed policy • Feasibility study Uniform distribution • LSM tree with 3 levels • L 0 = 1 Mb & fanout = 10 • Merge policy `Test’ s. t. • L 0 to L 1 merge – always Partial • L 1 to L 2 merge – always Full • Test policy beats Partial in some cases • Example: costs per level for index size = 20 Mb • Costs at L 2 – Test is slightly worse than Partial • Costs at L 1 – Test outperforms Partial by a large margin • Total savings is much better than Partial policy Index size = 20 Mb • Apply Full policy when Li+1 is small. • Extra costs in Full merge will be offset by future savings at upper levels. 29

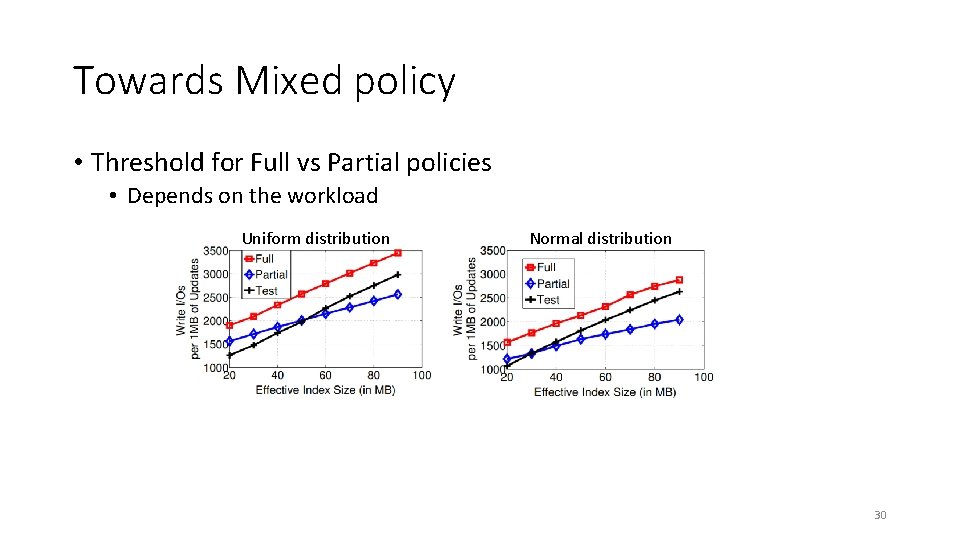
Towards Mixed policy • Threshold for Full vs Partial policies • Depends on the workload Uniform distribution Normal distribution 30

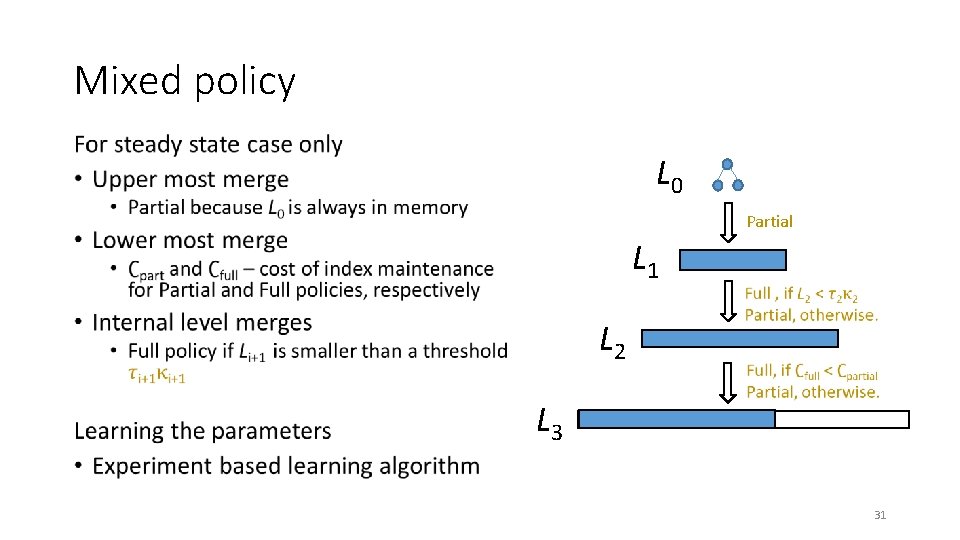
Mixed policy • L 0 Partial L 1 L 2 L 3 31

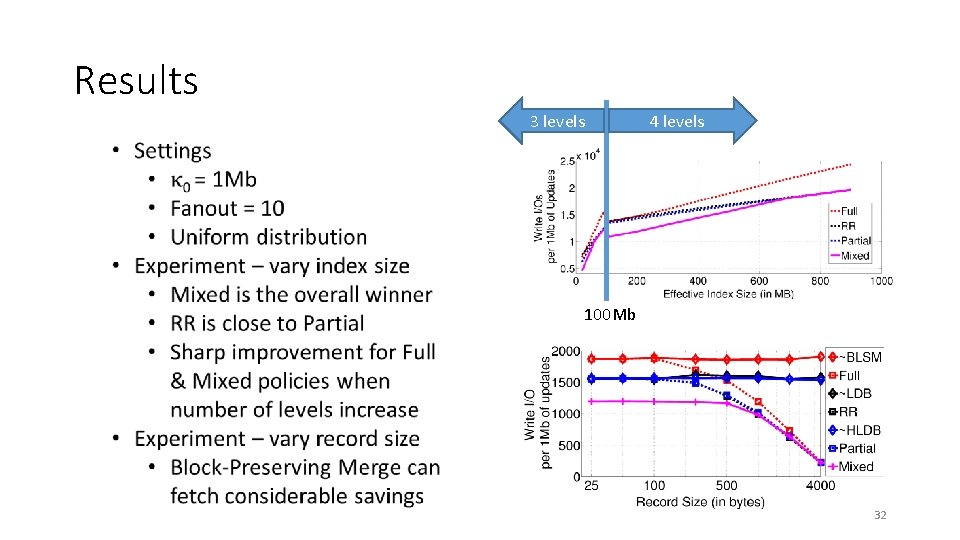
Results 3 levels 4 levels 100 Mb 32

Conclusion • Optimized LSM tree structure for Random Access Block Devices • Block-Preserving Merge for saving blocks during merge • Studied performance of merge policies – Full, RR and Partial • RR is surprisingly quite good • Introduced Mixed policy • More I/O savings 33

Outline • Permutation problem • Merge policies for Log-Structured Merge (LSM) tree • Concurrency control in indexes • Conclusion & future work [VLDB 2013] “Permuting Data on Random-Access Block Storage”. Risi Thonangi, Jun Yang [Techreport 2015] “Optimizing LSM-tree for Random- Access Block Storage”. Risi Thonangi, Jun Yang [CIKM 2012] “A Practical Concurrent Index for Solid-State Drives”. Risi Thonangi, Shivnath Babu, Jun Yang 34

Indexing schemes for SSDs • B+tree is sub-optimal for SSDs • Insertions/deletions require in-place updates • Thumb rule for index design on SSDs – avoid small in-place updates • Buffer insertions and deletions • Batch-reorganize the index when buffer overflows • Indexing schemes proposed for SSDs • BFTL, LA-tree, FD-tree, … • Have bad response times during index reorganizations 35

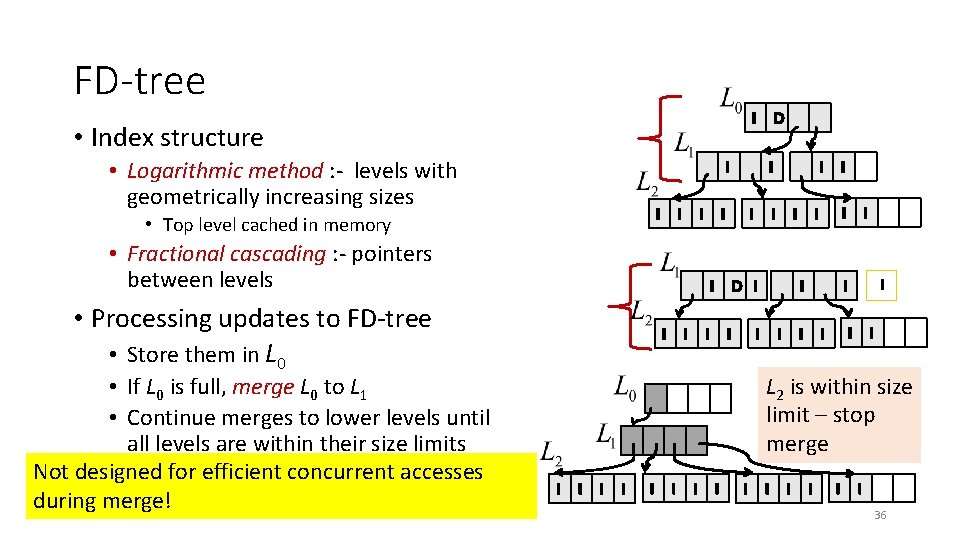
FD-tree I D • Index structure • Logarithmic method : - levels with geometrically increasing sizes I I I • Top level cached in memory • Fractional cascading : - pointers between levels • If L 0 is full, merge L 0 to L 1 • Continue merges to lower levels until all levels are within their size limits Not designed for efficient concurrent accesses during merge! I I I D I • Processing updates to FD-tree • Store them in L 0 I I I I I L 2 is within size limit – stop merge I I I I 36

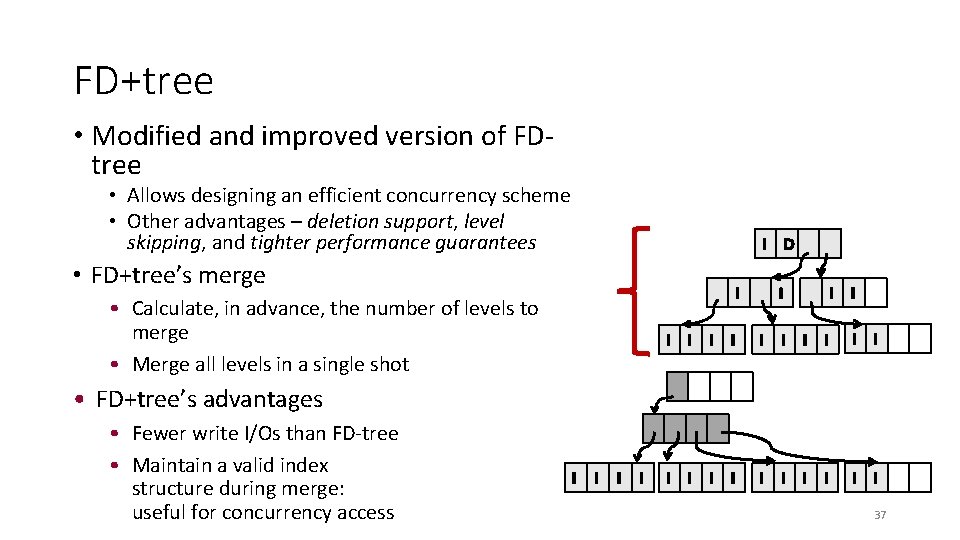
FD+tree • Modified and improved version of FDtree • Allows designing an efficient concurrency scheme • Other advantages – deletion support, level skipping, and tighter performance guarantees I D • FD+tree’s merge I • Calculate, in advance, the number of levels to merge • Merge all levels in a single shot I I I I I I • FD+tree’s advantages • Fewer write I/Os than FD-tree • Maintain a valid index structure during merge: useful for concurrency access I I 37

FD+FC – Full Concurrency for FD+tree • Goals : • Don’t want to use extra space • No coarse-grained locking of the tree • Idea : • Maintain a wavefront to track progress of merge • Delete blocks in old levels that were already merged • Lookups check wavefront and determine which levels to search wavefront I D I I I I I I I 38

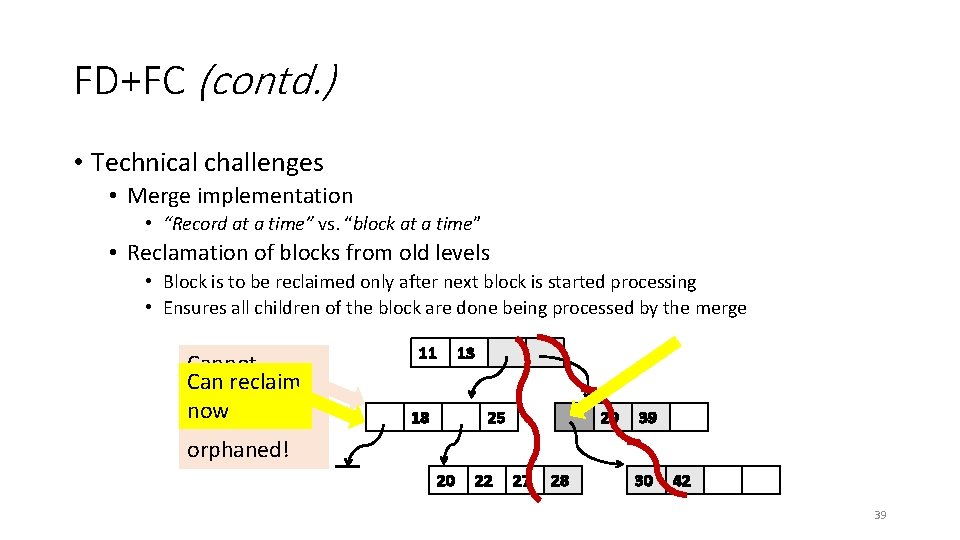
FD+FC (contd. ) • Technical challenges • Merge implementation • “Record at a time” vs. “block at a time” • Reclamation of blocks from old levels • Block is to be reclaimed only after next block is started processing • Ensures all children of the block are done being processed by the merge Cannot Can reclaim yet: now 28 would be orphaned! 11 18 13 25 20 22 29 27 28 39 30 42 39

FD+tree & FD+FC – more details • Level skipping • Utilizes main memory more efficiently • Proper deletion support + stronger performance guarantees • Merges do not read lock blocks 40

Experimental results FD+FC vs. FD+XM – global lock FD+DS – space doubling • Synthetic workloads • FD+FC is better for both inserts and lookups • FD+DS fares poorly for inserts 41

Conclusion • Concurrency control is important for SSD Indexes • Good concurrency control requires both • carefully rethinking index operations (FD+tree), and • designing fine-grained but low-overhead protocols (FD+FC) 42

Outline • Permutation problem • Merge policies for Log-Structured Merge (LSM) tree • Concurrency control in indexes • Conclusion & future work [VLDB 2013] “Permuting Data on Random-Access Block Storage”. Risi Thonangi, Jun Yang [Techreport 2015] “Optimizing LSM-tree for Random- Access Block Storage”. Risi Thonangi, Jun Yang [CIKM 2012] “A Practical Concurrent Index for Solid-State Drives”. Risi Thonangi, Shivnath Babu, Jun Yang 43

Conclusion & Future Work • Studied optimizations to database algorithms for Random Access Block Devices • Random access block devices as drop in replacement is good but sub-optimal • Optimizing database algorithms to random access and read/write asymmetry can fetch us considerably more savings – both cost & performance • Future work • Optimizing for multi-channel parallelism in random-access block devices • Utilizing on-disk computing resources for data processing tasks • Optimizing for Phase change RAM • Where should we fit PC-RAM in the storage architecture? • Explore how high to push the specializations in the system architecture • We’ve shown the benefit of specializing access methods and query processing algorithms • What about query optimization? 44

Thank you 45

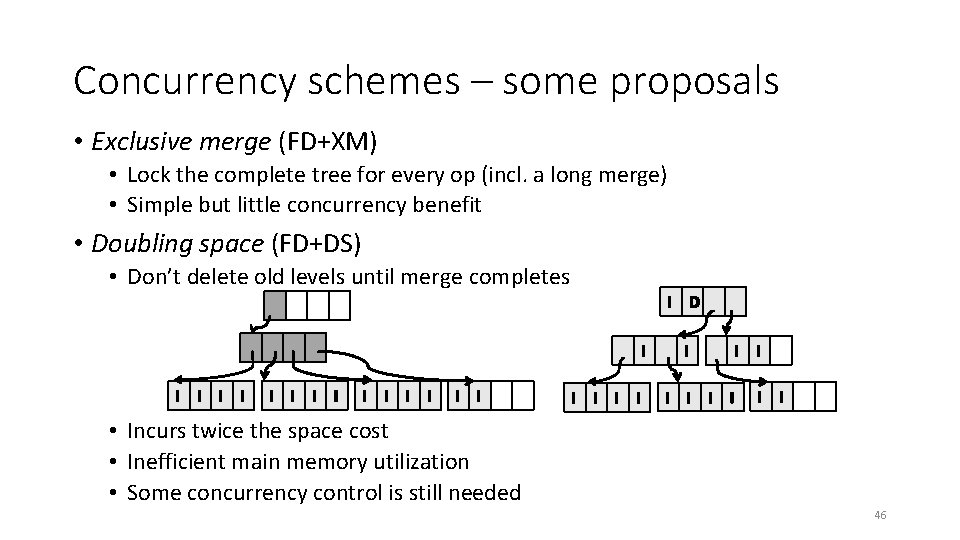
Concurrency schemes – some proposals • Exclusive merge (FD+XM) • Lock the complete tree for every op (incl. a long merge) • Simple but little concurrency benefit • Doubling space (FD+DS) • Don’t delete old levels until merge completes I D I I I I I I I • Incurs twice the space cost • Inefficient main memory utilization • Some concurrency control is still needed 46

Experimental results • Synthetic workloads • FD+FC is better for both inserts and lookups • FD+DS fares poorly for inserts • TPC-C like workloads • FD+FC worst-case Rp is less than a second • FD+DS worst-case Rp increases as size of database grows 47

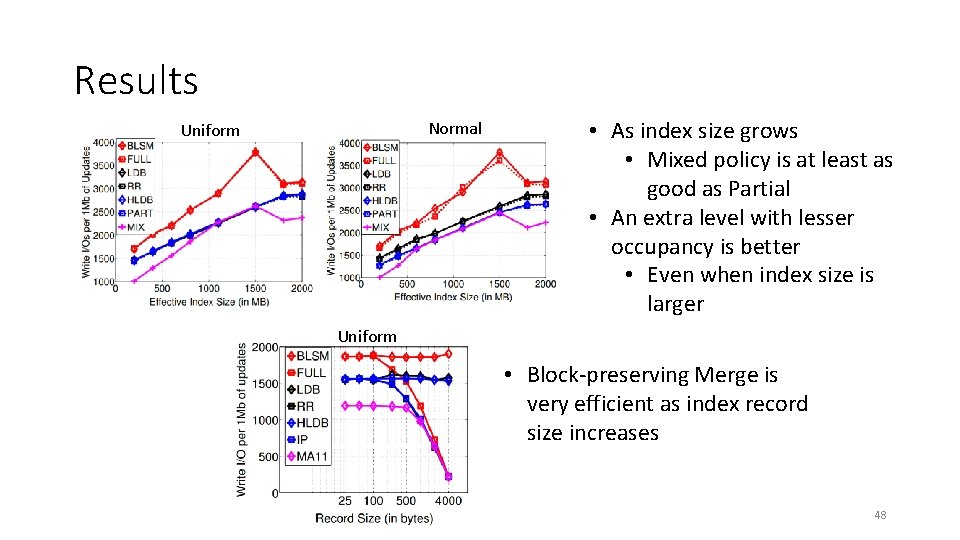
Results Normal Uniform • As index size grows • Mixed policy is at least as good as Partial • An extra level with lesser occupancy is better • Even when index size is larger Uniform • Block-preserving Merge is very efficient as index record size increases 48

⇒ Modified LSM-tree • To save blocks during merge • Merge policies – Full, Round Robin, Partial • Mixed merge policy • Combine Full and Partial for increased I/O savings • Results • Conclusion 49

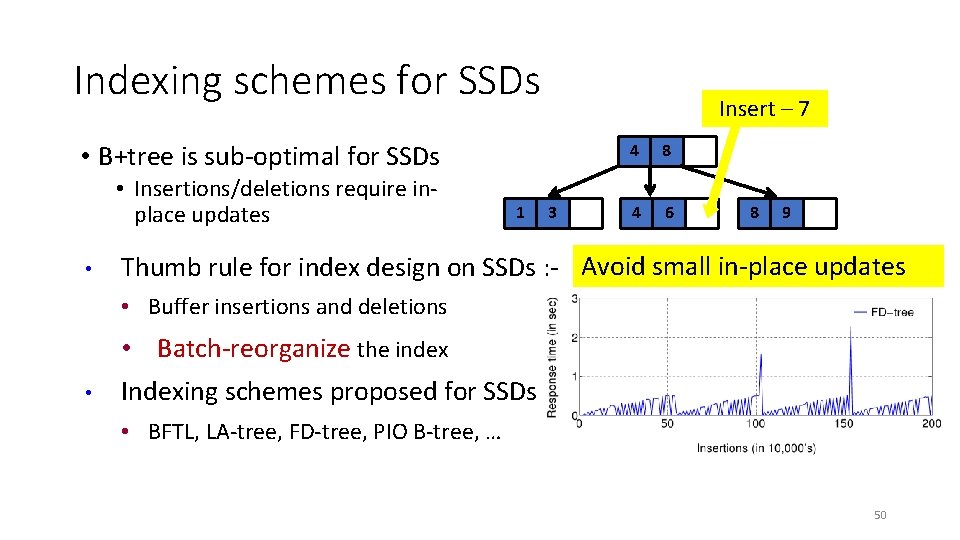
Indexing schemes for SSDs Insert – 7 • B+tree is sub-optimal for SSDs • Insertions/deletions require inplace updates • 1 3 4 8 4 6 8 9 Thumb rule for index design on SSDs : - Avoid small in-place updates • Buffer insertions and deletions • Batch-reorganize the index • Indexing schemes proposed for SSDs : • BFTL, LA-tree, FD-tree, PIO B-tree, … 50