Optimizing CTL Model checking Model checking TCTL CS

Optimizing CTL Model checking + Model checking TCTL CS 5270 Lecture 9 Lecture 8 1

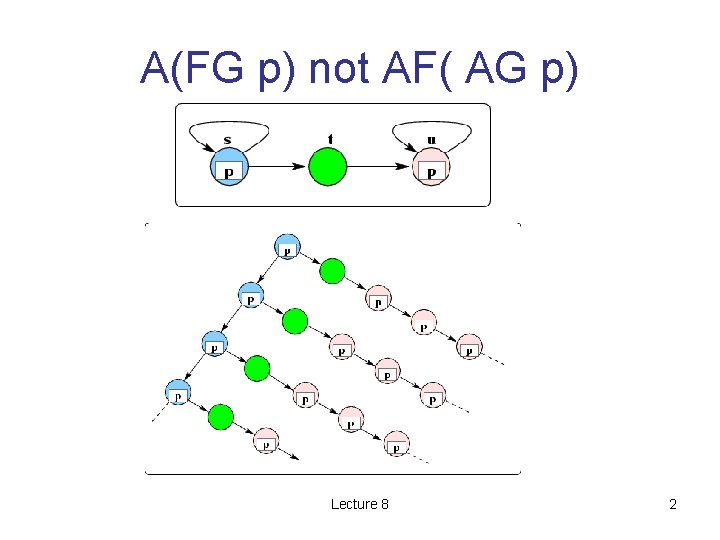
A(FG p) not AF( AG p) Lecture 8 2

Today… • Summary • Optimizations for model checking – ROBDDs • TCTL– Syntax – Semantics – Algorithm for MC – Optimizations Lecture 8 3

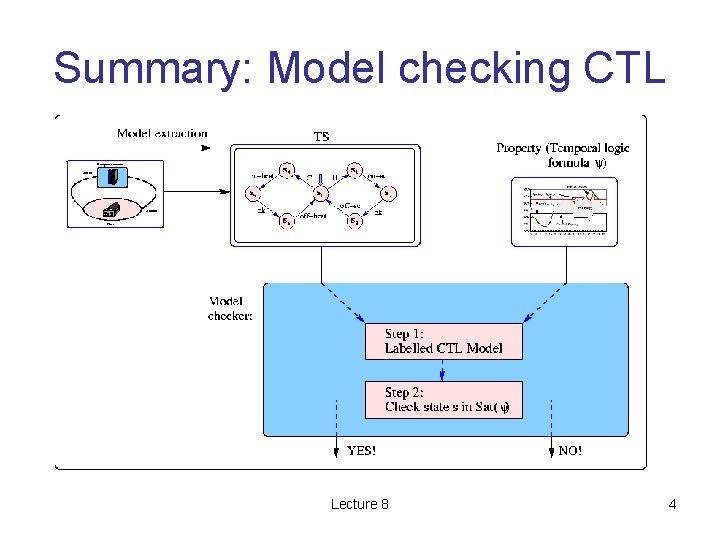
Summary: Model checking CTL Lecture 8 4

Optimization • The principal one: – Reduce to a problem with Boolean variables/Boolean formulæ • Is this reasonable? – Well – most modelling is done like this – even when you do have (non-boolean) variables – + efficiencies from efficient operations on boolean functions Lecture 8 5

States as boolean formulæ • Encode states using m boolean variables. – Allows for 2 m states. • For example: m=3: – S={s 1, s 2, s 3, s 4, s 5, s 6, s 7, s 8} • Propositional booleans a, b, c: – S={000, 001, 010, 011, 100, 101, 110, 111} – S = { a b c, a b c , … } Lecture 8 6

Transitions as boolean formulæ • Encode (s, s’) using before and after propositional boolean variables – a, b, c and a’, b’, c’. • For example: (s 1, s 4): – (s 1, s 4) = ( a b c) ( a’ b’ c’) Lecture 8 7

Sufficient for modelling? • Encode another mutual exclusion protocol • Two processes, P 1 and P 2 share booleans – Co-operate for mutual exclusion • Third process T 1 monitors and sets a turn variable • System is parallel composition: P 1 || P 2 || T 1 Lecture 8 8

Co-operative mutex: Process P 1 = if (idle 1) { wait 1 = true; idle 1 = false; } else if (wait 1 & idle 2) { active 1 = true; wait 1 = false; } else if (wait 1 & wait 2 & (!turn)) { active 1 = true; wait 1 = false; } if (active 1) { }; Crit. Sect(); idle 1 = true; active 1 = false; Lecture 8 ( followed by P 1 ) 9

Co-operative mutex: Process P 2 = if (idle 2) { wait 2 = true; idle 2 = false; } else if (wait 2 & idle 1) { active 2 = true; wait 2 = false; } else if (wait 2 & wait 1 & turn) { active 2 = true; wait 2 = false; } if (active 2) { }; Crit. Sect(); idle 2 = true; active 2 = false; Lecture 8 ( followed by P 2 ) 10

Co-operative mutex: Process T 1 = if (idle 1 & wait 2) { turn = true; } else if (idle 2 & wait 1) { Turn = false; }; ( followed by T 1 ) System = (P 1 || P 2 || T 1); System; Lecture 8 11

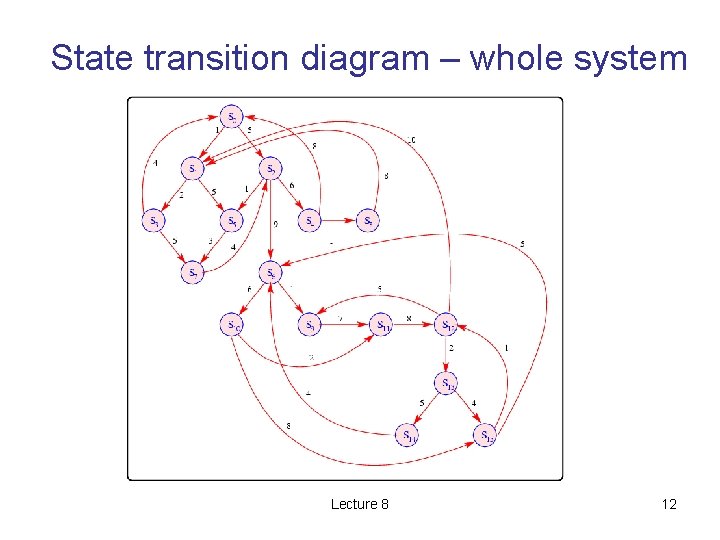
State transition diagram – whole system Lecture 8 12

Transitions as predicates • P 1 = (i 1 w 1’ i 1’) (w 1 i 2 a 1’ w 1’) (w 1 w 2 t a 1’ w 1’) (a 1 i 1’ a 1’) • P 2 = (i 2 w 2’ i 2’) (w 2 i 1 a 2’ w 2’) (w 2 w 1 t a 2’ w 2’) (a 2 i 2’ a 2’) • T 1 = (i 1 w 2 t’) (i 2 w 1 t’) Lecture 8 13

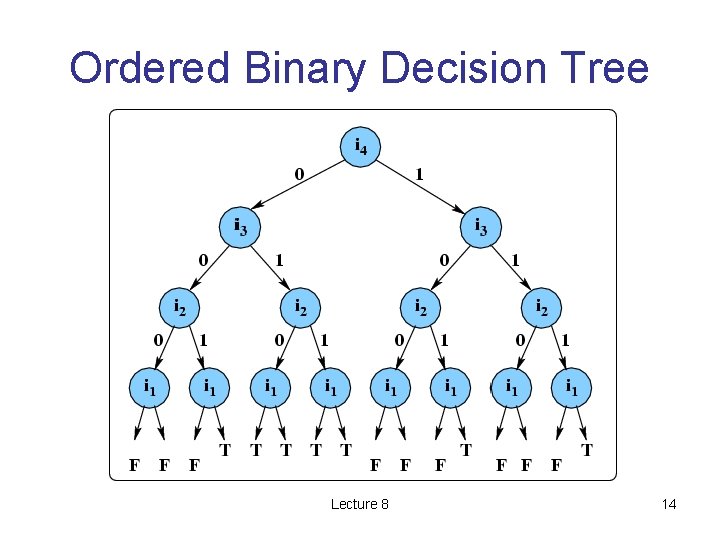
Ordered Binary Decision Tree Lecture 8 14

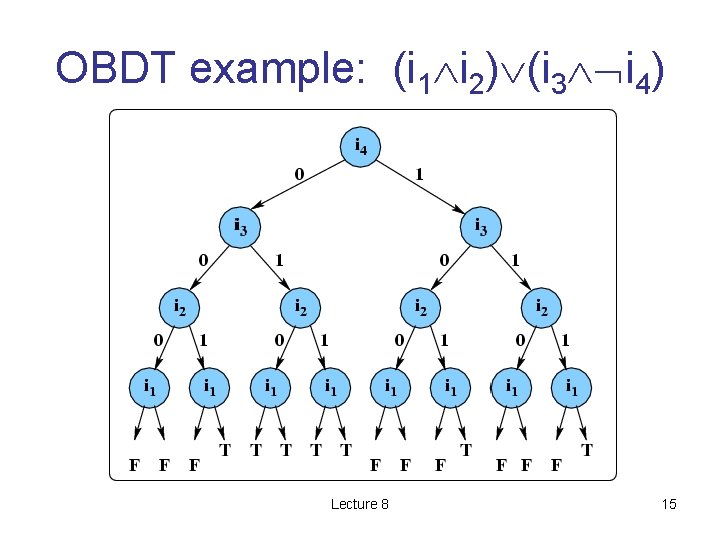
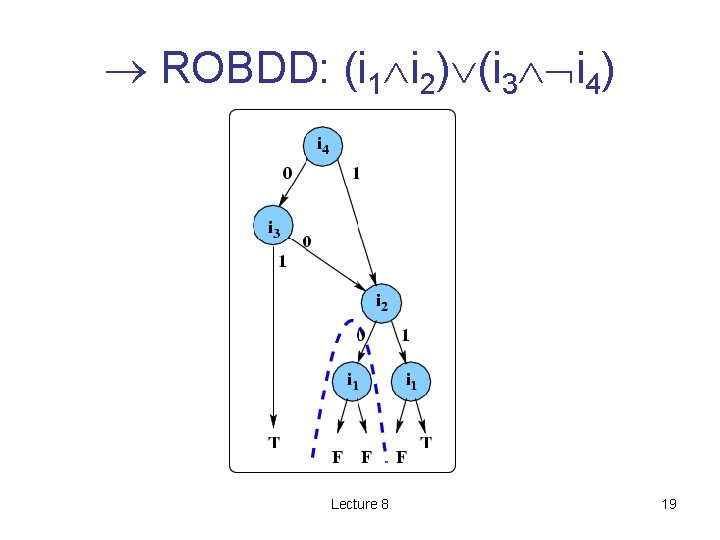
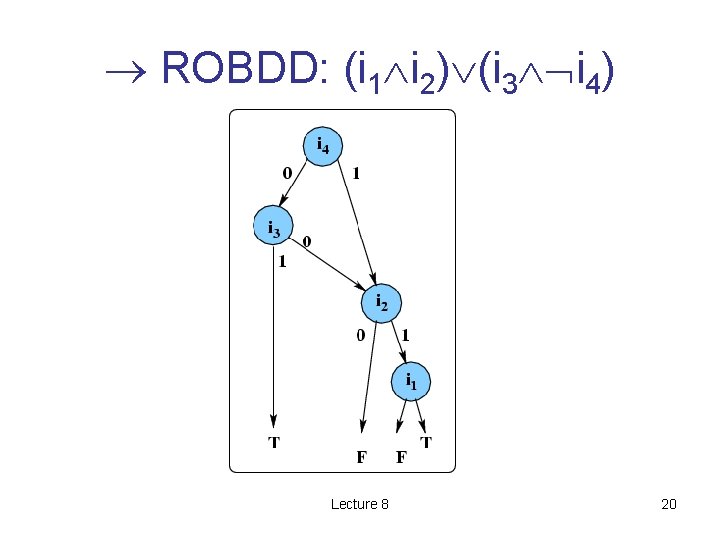
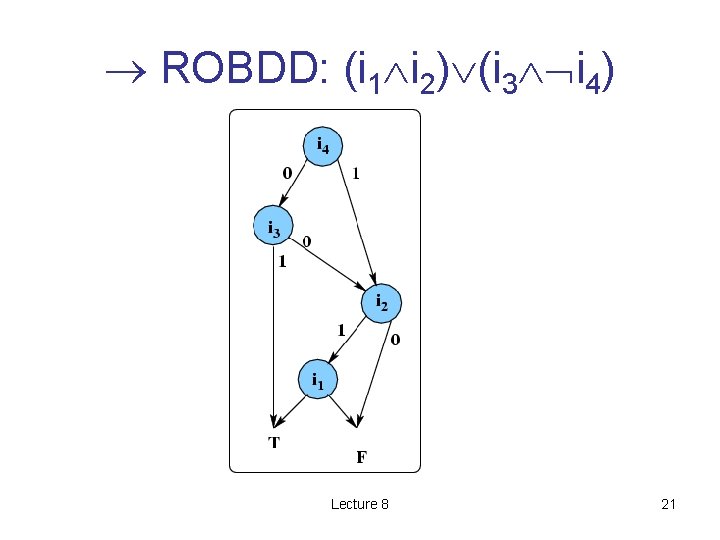
OBDT example: (i 1 i 2) (i 3 i 4) Lecture 8 15

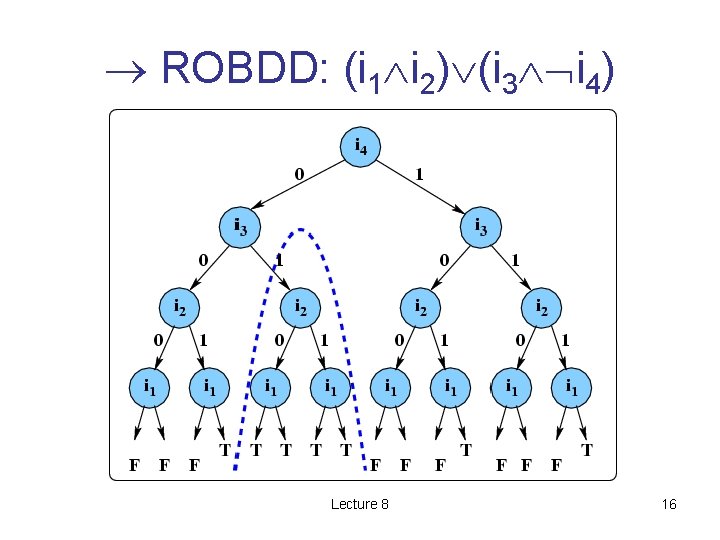
ROBDD: (i 1 i 2) (i 3 i 4) Lecture 8 16

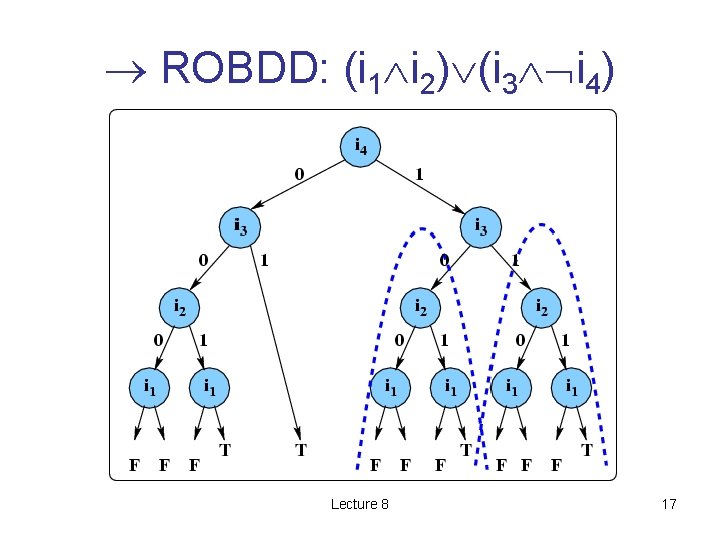
ROBDD: (i 1 i 2) (i 3 i 4) Lecture 8 17

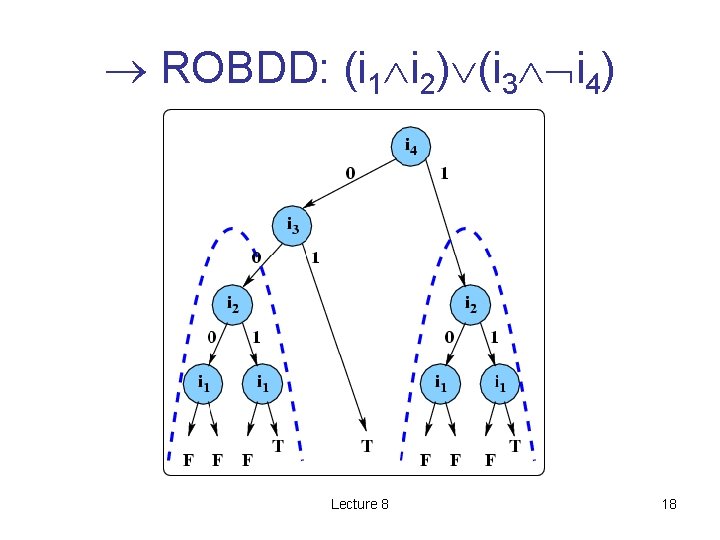
ROBDD: (i 1 i 2) (i 3 i 4) Lecture 8 18

ROBDD: (i 1 i 2) (i 3 i 4) Lecture 8 19

ROBDD: (i 1 i 2) (i 3 i 4) Lecture 8 20

ROBDD: (i 1 i 2) (i 3 i 4) Lecture 8 21

History… • The ROBDD optimization originally by Bryant (86) – paper on boolean graphs • The application to model checking by Mc. Millan (Originally in late 80’s – subject of thesis in 1992) • smv – Symbolic model verifier – originally by Mc. Millan Lecture 8 22

Today… • Summary • Optimizations for model checking – ROBDDs • TCTL– Syntax – Semantics – Algorithm for MC – Optimizations Lecture 8 23

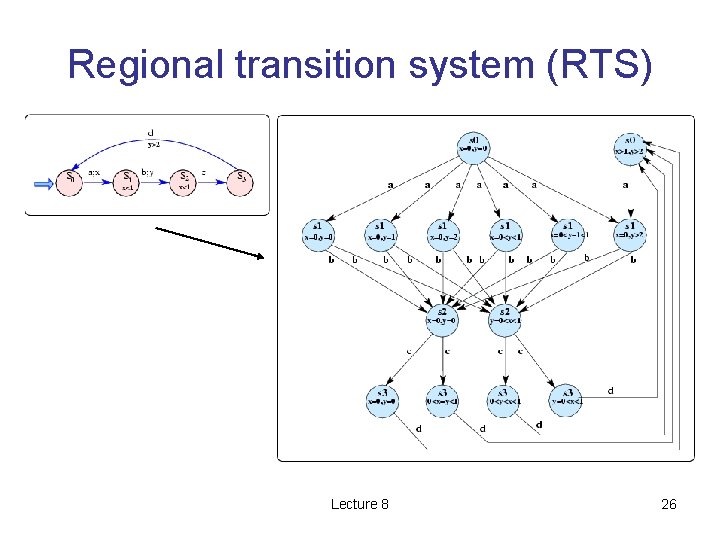
Regional transition system (RTS) • Given TATTS = (s, s 0, Act, ), then the RTS is a quotiented transition system RTS = (Ř, Ř 0, Act, ), where Ř = {(s, [v]t) | (s, v) s [v] t REGv}, and Ř 0 = {(s, [v]t) | (s, v) s 0 [v] t REGv}, and a • finally, (s, [v]t) (s’, [v’]t) if and only if there is a transition (s, v) a (s’, v’) in TATTS. Lecture 8 24

Regional transition system (RTS) • Notation: Ř – a set of regions ř – a particular region in the set: r – a particular valuation: Lecture 8 (s, [v]t) (s, v) 25

Regional transition system (RTS) Lecture 8 26

Kripke structure/model for TCTL • Def: A TCTL model over a set of atomic propositions AP is the 4 -tuple (Ř, Δ, AP, L) – – Ř – finite set of regions from RTS Δ Ř Ř - a total transition relation AP – a finite set of atomic propositions L: Ř → 2 AP – A labelling function which labels each region with the propositions true in that region Note that the propositions may include clock constraints… Lecture 8 27

TCTL- syntax • Given p AP, x X (model clock variables), z Z (property clock variables), (X Z) (clock constraints), then p and are TCTL- formulæ, and if 1 and 2 are TCTL- formulæ then so are: • • • 1 1 2 z in 1 A( 1 U 2 ) E( 1 U 2 ) Lecture 8 28

TCTL examples • Note: temporal operators can be subscripted: • A( 1 U<7 2 ) means 1 holds until (within 7 time units) 2 becomes true. • Implemented as: z in A( ( 1 z<7) U 2 ) • A( alarm U<7 boiler-off ): the alarm is on until (within 7 time units) the boiler-off is signaled. • EF<7( alarm ) = E( true U<7 alarm ): the alarm will be on within 7 time units. Lecture 8 29

Semantics of TCTL • Expressed in terms of a model, and the modelling relation ² which links a model, a composite state r=(s, v) and a formula clock valuation with a property. • M, (r, f) ² P - means that (TCTL) property P holds in (or is satisfied in) state r in the case of a formula valuation f for a given model M Lecture 8 30

(Inductive) definition of ² M, (r, f) ² P M, (r, f) ² 1 2 p L(ř) v f² (M, (r, f) ² 1 ) M, (r, f) ² 1, and M, (r, f) ² 2 M, (r, f) ² 1, or M, (r, f) ² 2 Lecture 8 31

(Inductive) definition of ² • M, (r, f) ² z in 1 M, (r, z in f) ² 1 – The notation z in f asserts that z is reset to 0 whenever it appears in the formula f • M, (r, f) ² A( 1 U 2 ) for every path from r, for some j, M, (j) ² 2, and i<j, M, (i) ² 1 2. Lecture 8 32

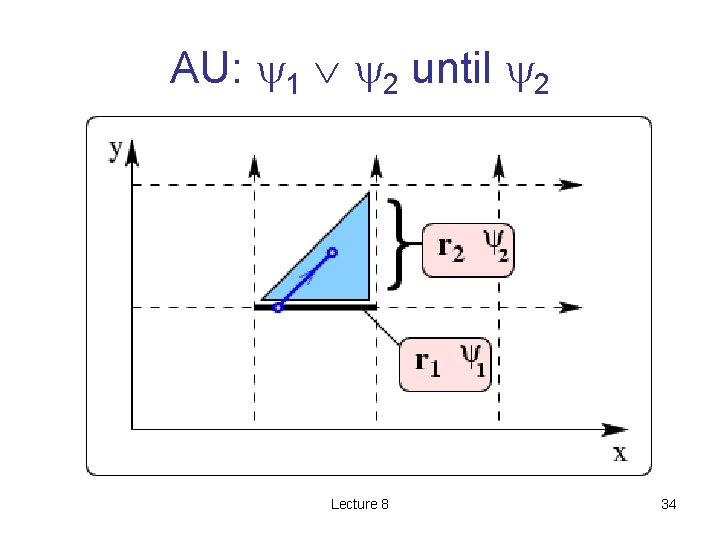
(Inductive) definition of ² • M, (r, f) ² E( 1 U 2 ) for one path from r, for some j, M, (j) ² 2, and i<j, M, (i) ² 1 2. – Note that in both EU and AU, the condition up until 2 is 1 2. and not just 1!! Lecture 8 33

AU: 1 2 until 2 Lecture 8 34

Model checking TCTL • Definition of a labelling algorithm in the notes – not much different from CTL • The only problem is this definition uses a least fixpoint iteration over an infinite set… • In practice use the region construction… Lecture 8 35

Optimization for TCTL MC • We have already seen the steps to create a (finite) regional automaton • Apart from that there is no magic bullet, and real-time model checking has an equivalent region-space explosion • For this reason, limit the size of systems • … so far … Lecture 8 36

Uppaal – more formally • TCTL, but with restrictions that amount to only safety (reachability) formulæ: – Set of clock constraints Z in formula is {} – Syntax just AG( ) and EF( ) (outer level) – : : = a | x op n | | 1 2 (op { , , }) – a is a location in the model • Other properties (bounded liveness…) require extended models/automatons: – compare system model with other test model Lecture 8 37