Optimizations for a Simulator Construction System Supporting Reusable

Optimizations for a Simulator Construction System Supporting Reusable Components David A. Penry and David I. August The Liberty Architecture Research Group Princeton University

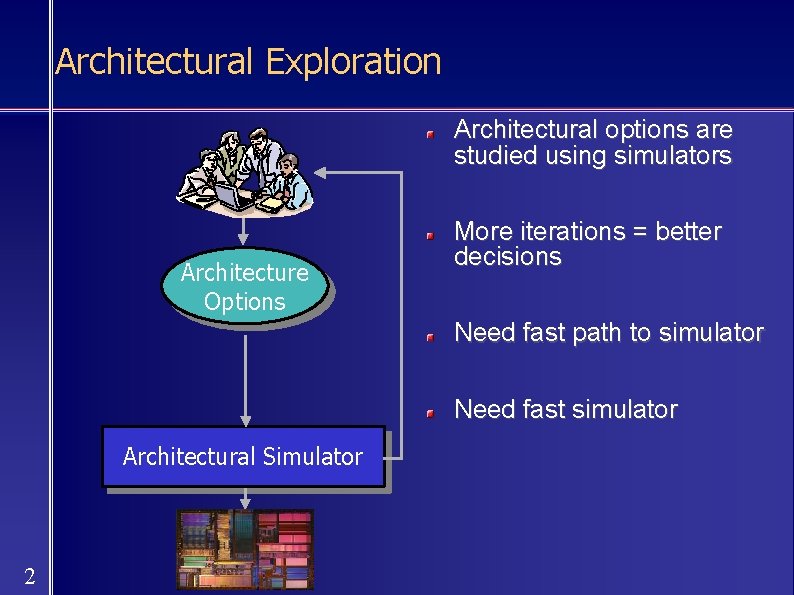
Architectural Exploration Architectural options are studied using simulators Architecture Options More iterations = better decisions Need fast path to simulator Need fast simulator Architectural Simulator 2

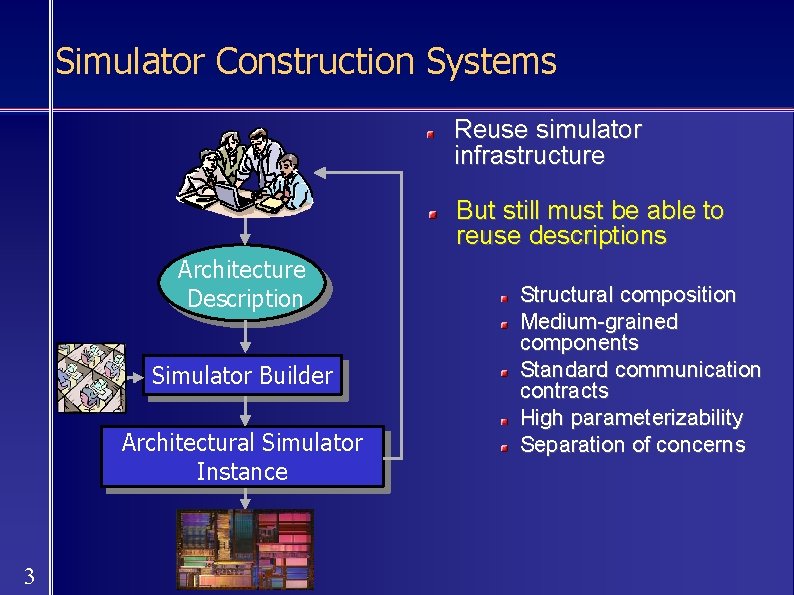
Simulator Construction Systems Reuse simulator infrastructure But still must be able to reuse descriptions Architecture Description Simulator Builder Architectural Simulator Instance 3 Structural composition Medium-grained components Standard communication contracts High parameterizability Separation of concerns

The Reuse Penalty Reusability leads to a speed penalty: more component instances more signals more general code Therefore: reusable systems are often slower How can we mitigate the reuse penalty? 4

Liberty Simulation Environment Simulator construction system for high reuse Two-tiered specifications Leaf module templates in C Netlisting language for instantiation and customization Three-signal standard communications contract with overrides (control functions) Data Enable Ack Code is generated 5

Contrast: System. C Simulator construction libraries (C++) Partially supports reuse: + Structural composition + Module granularity varies ? Communications contracts by convention - Low parameterizability - Separation of concerns Description is a C++ program 6

Models of Computation System C uses Discrete Event (DE) LSE uses Heterogenous Synchronous Reactive (HSR) Edwards (1997) Unparsed code blocks (black boxes) Values begin unresolved and resolve monotonically Chaotic scheduling A C B D 7

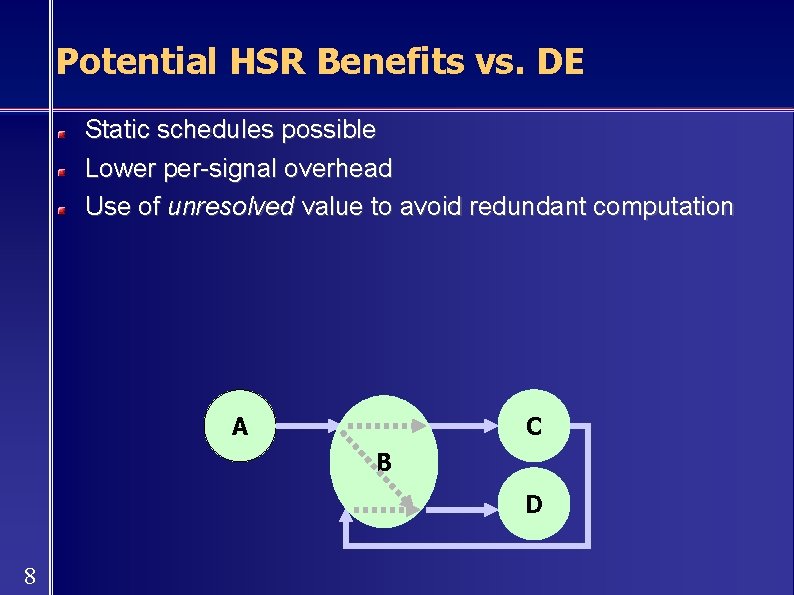
Potential HSR Benefits vs. DE Static schedules possible Lower per-signal overhead Use of unresolved value to avoid redundant computation A C B D 8

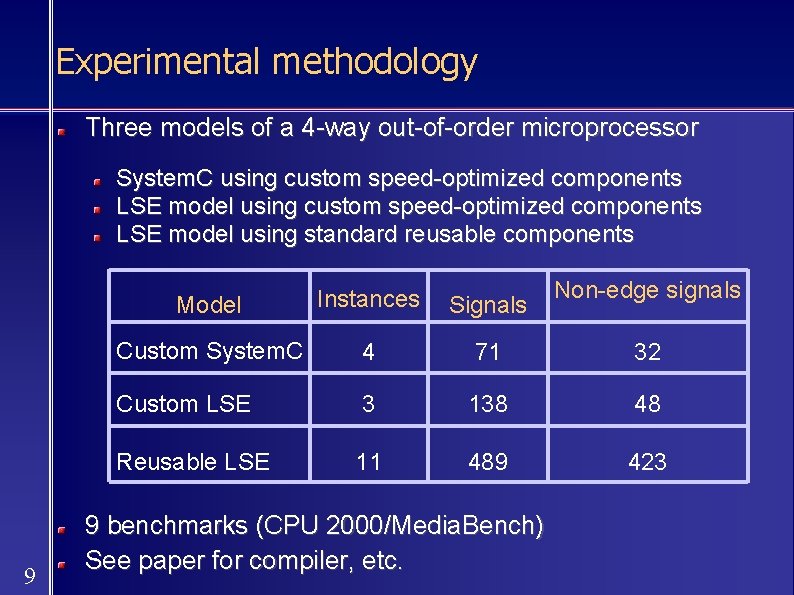
Experimental methodology Three models of a 4 -way out-of-order microprocessor System. C using custom speed-optimized components LSE model using standard reusable components 9 Non-edge signals Model Instances Signals Custom System. C 4 71 32 Custom LSE 3 138 48 Reusable LSE 11 489 423 9 benchmarks (CPU 2000/Media. Bench) See paper for compiler, etc.

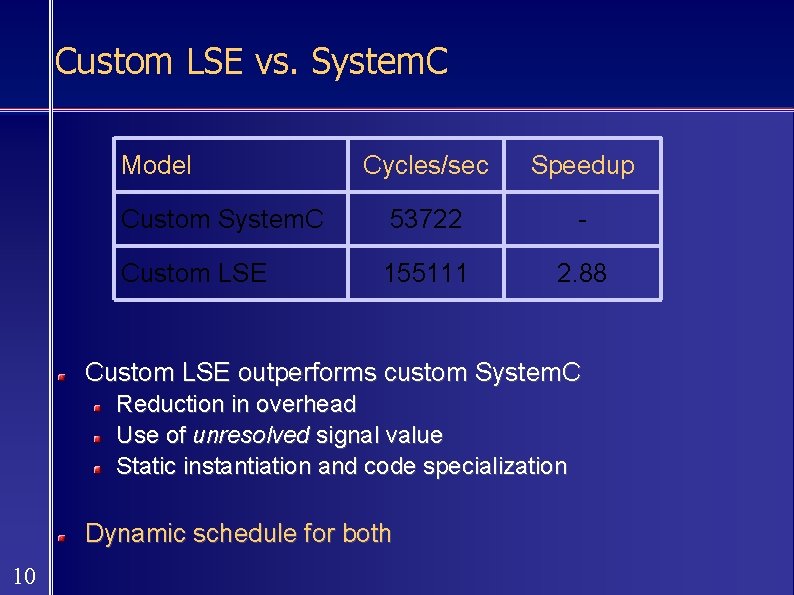
Custom LSE vs. System. C Model Cycles/sec Speedup Custom System. C 53722 - Custom LSE 155111 2. 88 Custom LSE outperforms custom System. C Reduction in overhead Use of unresolved signal value Static instantiation and code specialization Dynamic schedule for both 10

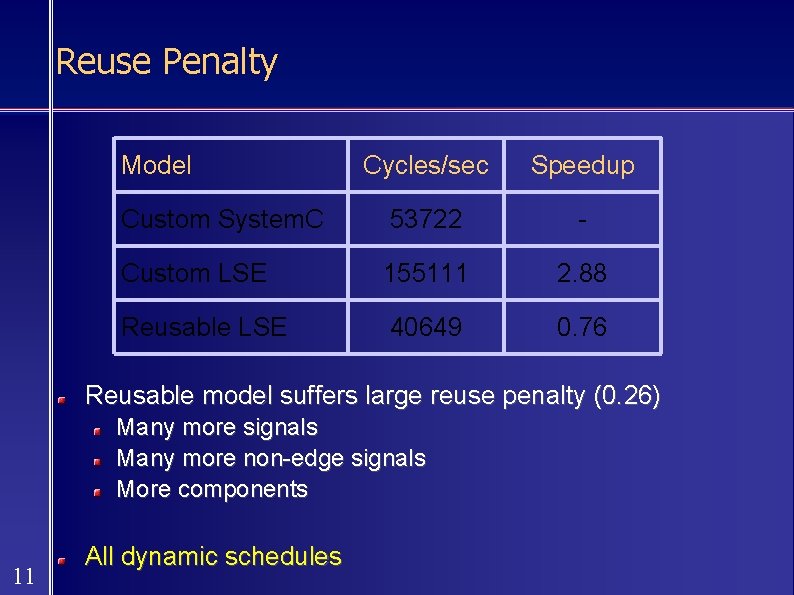
Reuse Penalty Model Cycles/sec Speedup Custom System. C 53722 - Custom LSE 155111 2. 88 Reusable LSE 40649 0. 76 Reusable model suffers large reuse penalty (0. 26) Many more signals Many more non-edge signals More components 11 All dynamic schedules

Creating Static Schedules Edward’s algorithm (1997) Construct a signal dependency graph Break into strongly-connected components (SCC). Schedule in topological order Partition each SCC into a head and tail Schedule tail recursively, then repeat head (any order) and tail’s schedule Coalesce A C B D 12

Creating Static Schedules Edward’s algorithm (1997) Construct a signal dependency graph Break into strongly-connected components (SCC). Schedule in topological order Partition each SCC into a head and tail Schedule tail recursively, then repeat head (any order) and tail’s schedule Coalesce 2 A 13 1 2 B 4 C D 1 3 3 4

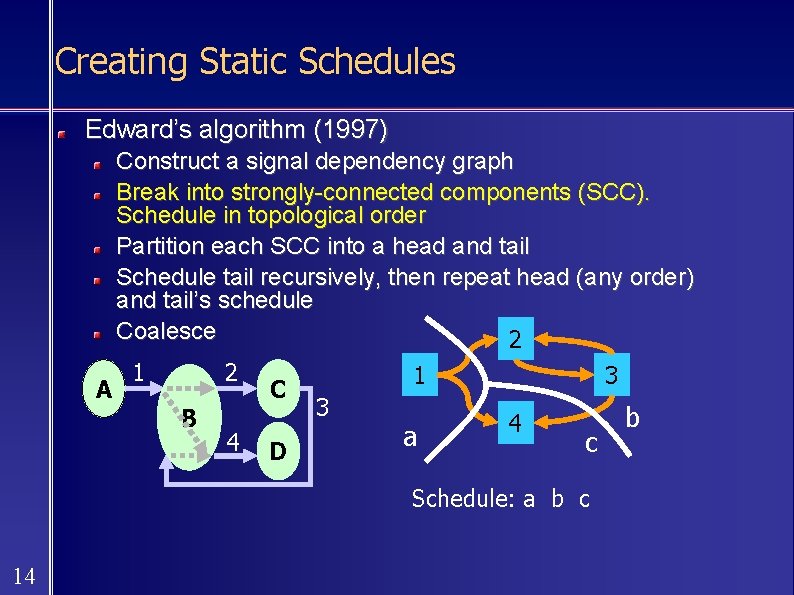
Creating Static Schedules Edward’s algorithm (1997) Construct a signal dependency graph Break into strongly-connected components (SCC). Schedule in topological order Partition each SCC into a head and tail Schedule tail recursively, then repeat head (any order) and tail’s schedule Coalesce 2 A 1 2 B 4 C D 1 3 a 3 4 c Schedule: a b c 14 b

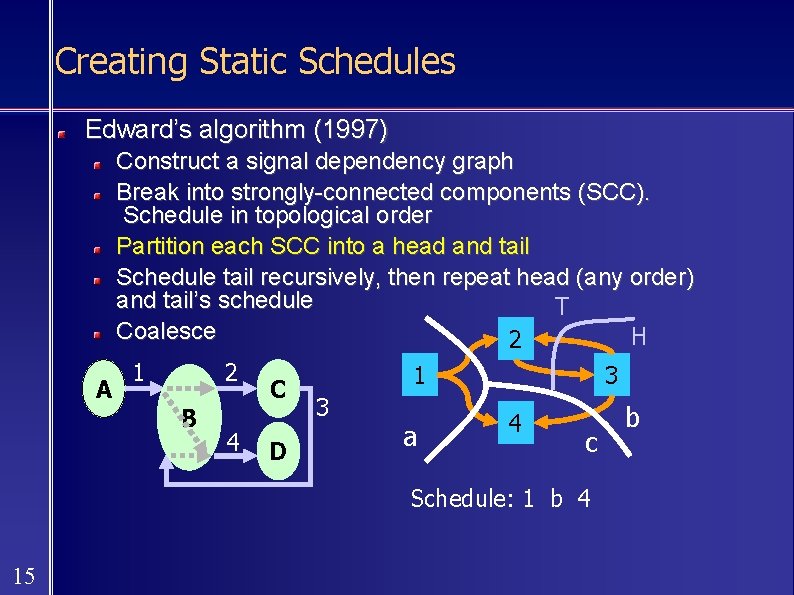
Creating Static Schedules Edward’s algorithm (1997) Construct a signal dependency graph Break into strongly-connected components (SCC). Schedule in topological order Partition each SCC into a head and tail Schedule tail recursively, then repeat head (any order) and tail’s schedule T Coalesce H 2 1 3 A C 3 B b 4 a 4 D c Schedule: 1 b 4 15

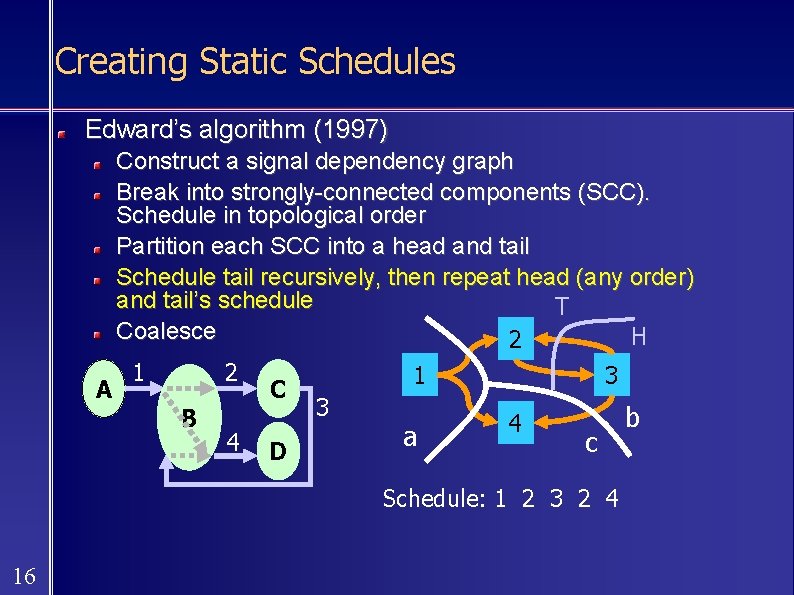
Creating Static Schedules Edward’s algorithm (1997) Construct a signal dependency graph Break into strongly-connected components (SCC). Schedule in topological order Partition each SCC into a head and tail Schedule tail recursively, then repeat head (any order) and tail’s schedule T Coalesce H 2 1 3 A C 3 B b 4 a 4 D c Schedule: 1 2 3 2 4 16

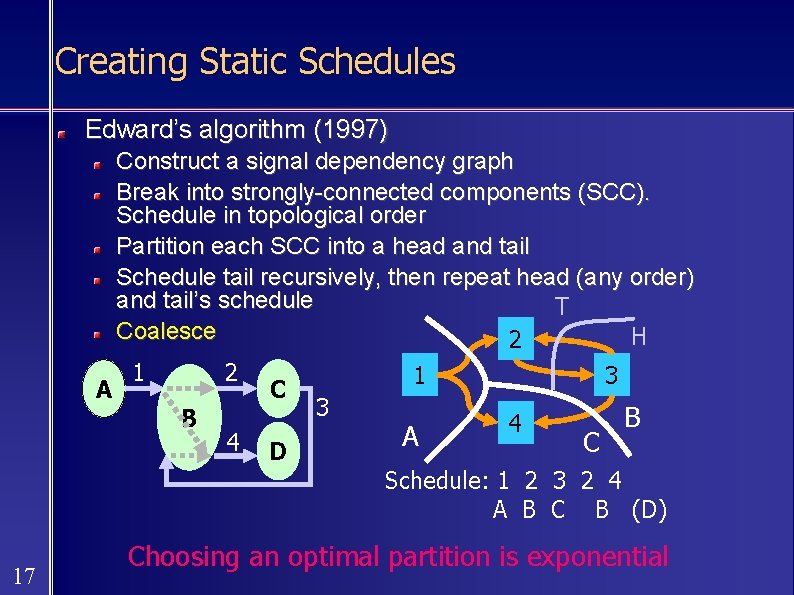
Creating Static Schedules Edward’s algorithm (1997) Construct a signal dependency graph Break into strongly-connected components (SCC). Schedule in topological order Partition each SCC into a head and tail Schedule tail recursively, then repeat head (any order) and tail’s schedule T Coalesce H 2 1 3 A C 3 B B 4 A 4 D C Schedule: 1 2 3 2 4 A B C B (D) 17 Choosing an optimal partition is exponential

Dynamic sub-schedule embedding SCCs arise due to incomplete information “Optimal” schedules are optimal w. r. t. information “Optimal” schedule may be worse than dynamic A B 18 C When an SCC is “too big”, just schedule that section dynamically

Dependency information enchancement In practice, we see big SCCs Peek in the black box Simple parsing of communication overrides (control functions) Can ask user to tell about internal dependencies Not too painful because it is reused A B 19 C

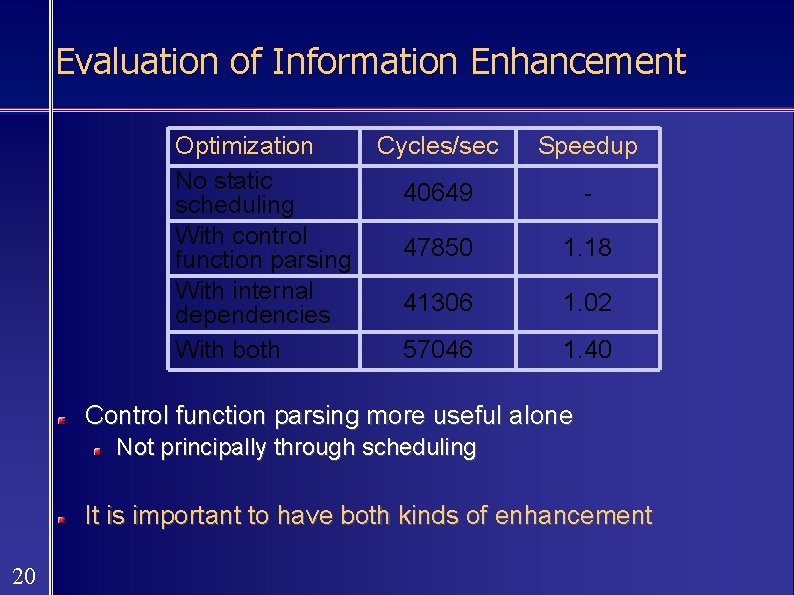
Evaluation of Information Enhancement Optimization No static scheduling With control function parsing With internal dependencies With both Cycles/sec Speedup 40649 - 47850 1. 18 41306 1. 02 57046 1. 40 Control function parsing more useful alone Not principally through scheduling It is important to have both kinds of enhancement 20

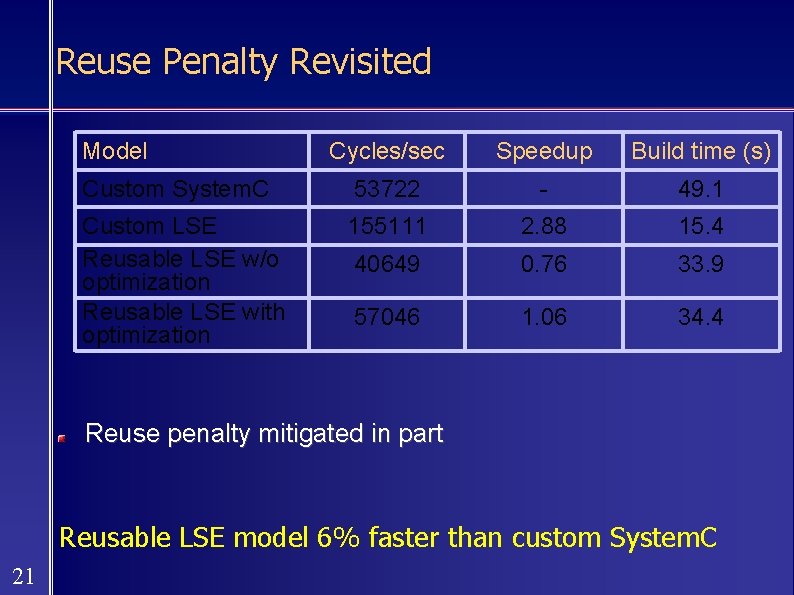
Reuse Penalty Revisited Model Cycles/sec Speedup Build time (s) Custom System. C 53722 - 49. 1 Custom LSE Reusable LSE w/o optimization Reusable LSE with optimization 155111 2. 88 15. 4 40649 0. 76 33. 9 57046 1. 06 34. 4 Reuse penalty mitigated in part Reusable LSE model 6% faster than custom System. C 21

Conclusions A tradeoff exists between speed and reuse The simulator construction system can help Higher base speed makes reuse penalty less painful Optimizations are possible with HSR model Ability of scheduler adapt to information available is powerful This adaptation is not possible with DE You can have high reuse at reasonable speeds 22

Future Work Release of LSE Fall 2003 http: //liberty. princeton. edu Hybrid model of computation Embed HSR in DE, DE in HSR Automatic extraction of HSR portions from DE 23

Other optimizations Improved block coalescing See paper Code specialization Implementation of APIs depends upon environment 24