Optimization Using Matrix Geometric and Cutting Plane Methods

Optimization Using Matrix Geometric and Cutting Plane Methods Sachin Jayaswal Beth Jewkes Department of Management Sciences University of Waterloo & Saibal Ray Desautels Faculty of Management Mc. Gill University

Outline • Motivation • Model Description • Mathematical Model • Solution Approach • Sample Results & Insights • Further Research 2

Motivation • A firm selling 2 substitutable products • Market sensitive to price and time • How to price the two products? 3

Real-Life Situations Courier Service – Fed. Ex Ground – Fed. Ex Custom Critical 4

Real-Life Situations Online shopping – Express Delivery – Priority Delivery 5

Real-Life Situations Call Centers – Ordinary Calls – Priority Calls 6

Problem Statement • A firm selling 2 substitutable products: – 1: priority product – 2: normal product • Market sensitive to price and time • Shared production capacity • Industry standard delivery time for product 2 • Decisions: – Delivery time guarantee for product 1? – Prices for product 1 and product 2? 7

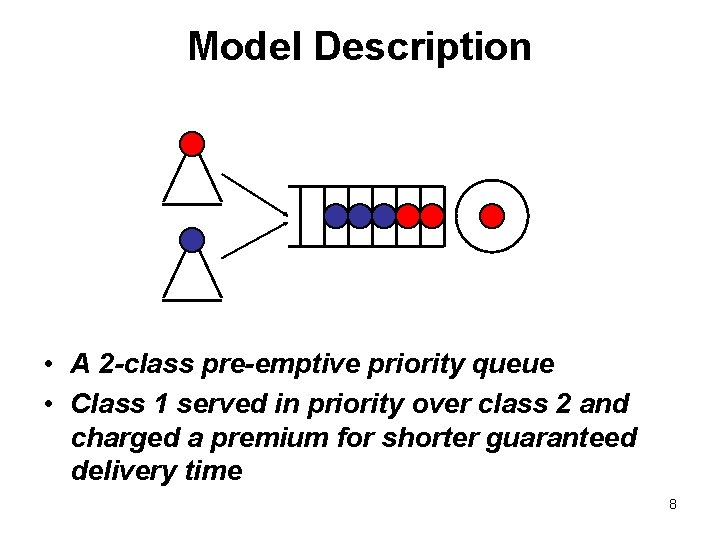
Model Description • A 2 -class pre-emptive priority queue • Class 1 served in priority over class 2 and charged a premium for shorter guaranteed delivery time 8

Notations • • • pi : price for class i Li : delivery time for class i λi : demand rate (exponential) for class i µ : service rate (exponential) m : unit operating cost Π : profit per unit time for the firm A : marginal capacity cost Wi: waiting time (in queue + service) of class i Si : delivery time reliability level, P(Wi <= Li) 9

Model Description • Demand: – Exponential with rates λ 1 and λ 2 – price and delivery time sensitive 10

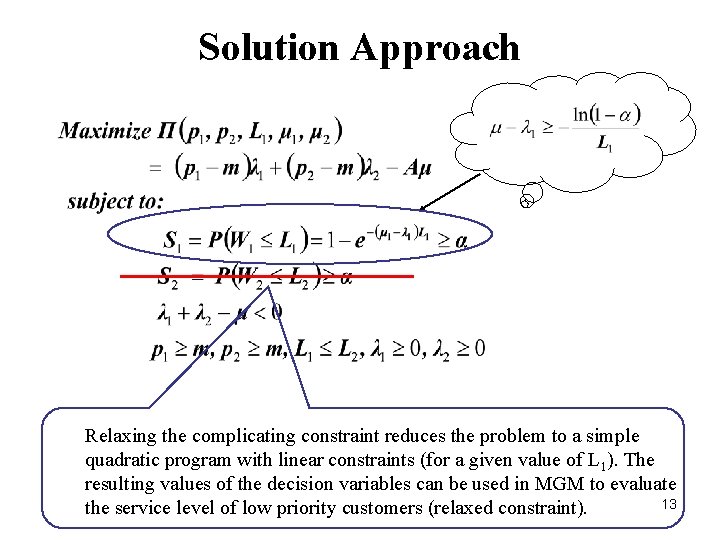
Mathematical Model How to use the numerical results in mathematical model for optimization? How to express this constraint analytically? This can be evaluated numerically using matrix-geometric method (MGM). 11

Solution Approach: Literature Review • Atalson, Epelman & Henderson (2004): Call center staffing with simulation and cutting plane methods • Henderson & Mason (1998): Rostering by integer programming and simulation • Morito, Koida, Iwama, Sato & Tamura (1999): Simulation based constraint generation with applications to optimization of logistic system design 12

Solution Approach Relaxing the complicating constraint reduces the problem to a simple quadratic program with linear constraints (for a given value of L 1). The resulting values of the decision variables can be used in MGM to evaluate 13 the service level of low priority customers (relaxed constraint).

Matrix Geometric Method for service level of low priority customers • State Variables: – N 1(t): Number of high priority customers in the system (including the one in service) – N 2(t): Number of low priority customers in the system (including the one in service) 14

Matrix Geometric Method for service level of low priority customers 15

Rate Matrix 16

Rate Matrix 17

Rate Matrix 18

Matrix Geometric Method 19

Matrix Geometric Method 20

Matrix Geometric Method 21

Service level of low priority customers 22

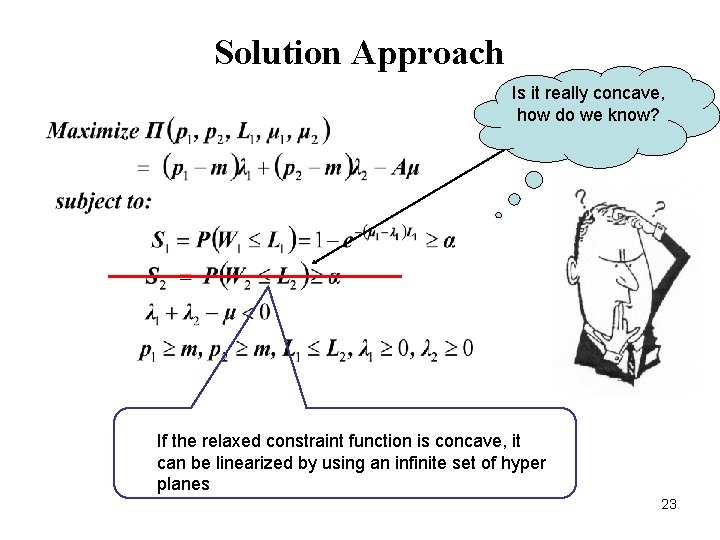
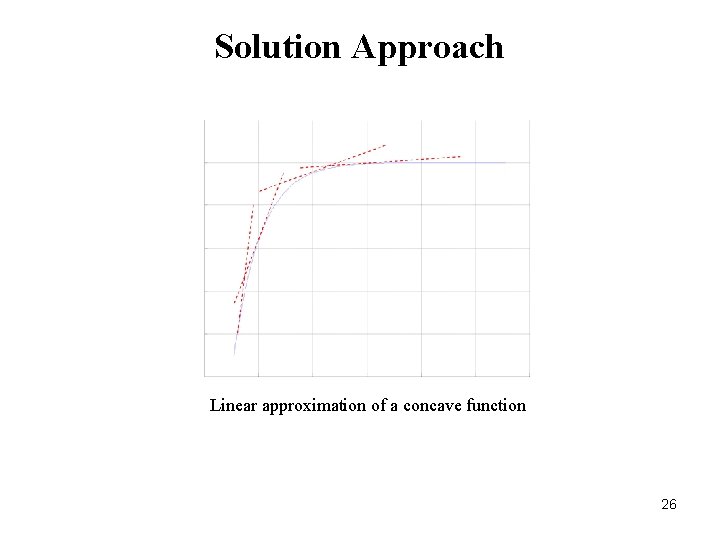
Solution Approach Is it really concave, how do we know? If the relaxed constraint function is concave, it can be linearized by using an infinite set of hyper planes 23

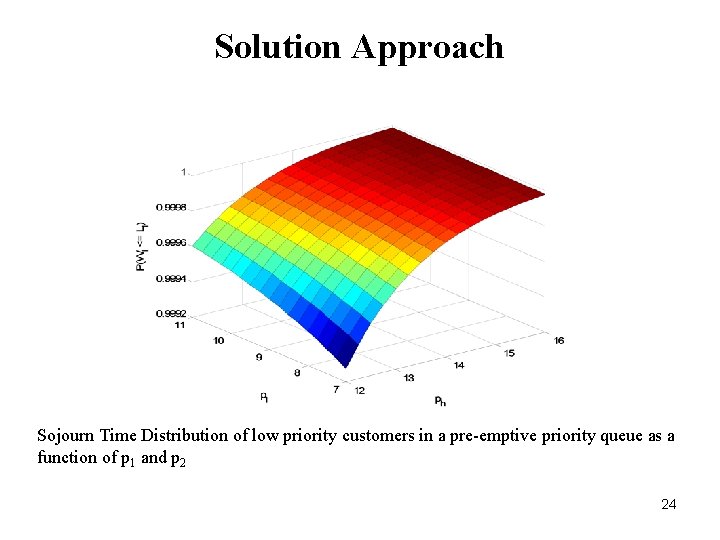
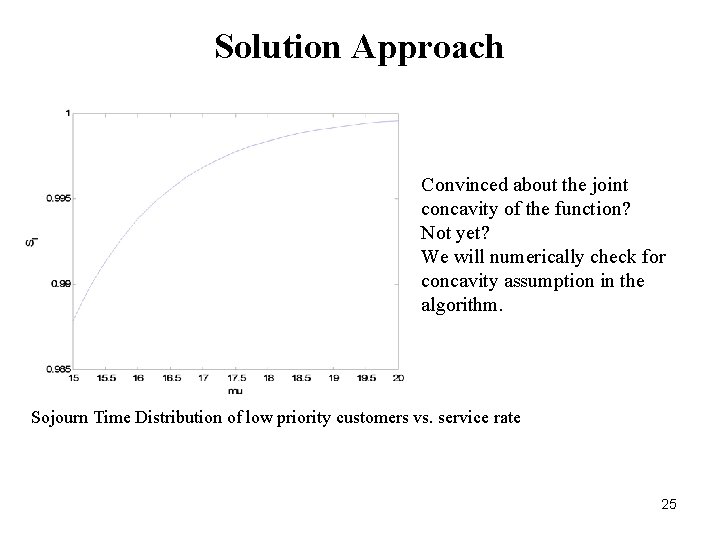
Solution Approach Sojourn Time Distribution of low priority customers in a pre-emptive priority queue as a function of p 1 and p 2 24

Solution Approach Convinced about the joint concavity of the function? Not yet? We will numerically check for concavity assumption in the algorithm. Sojourn Time Distribution of low priority customers vs. service rate 25

Solution Approach Linear approximation of a concave function 26

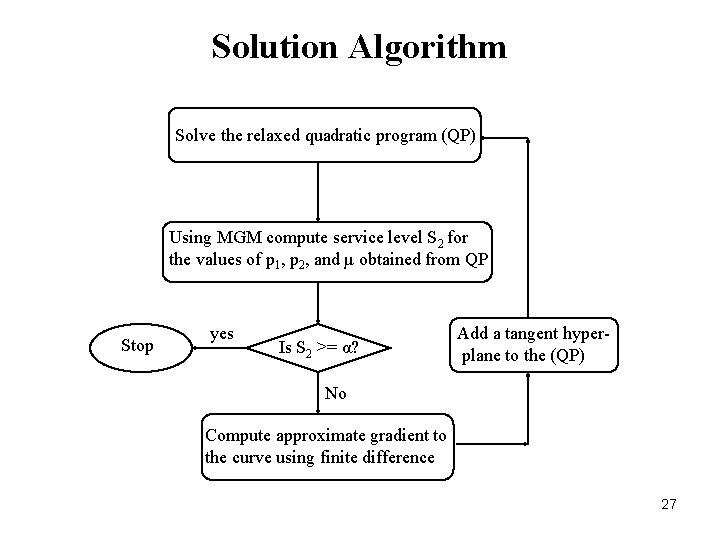
Solution Algorithm Solve the relaxed quadratic program (QP) Using MGM compute service level S 2 for the values of p 1, p 2, and µ obtained from QP Stop yes Is S 2 >= α? Add a tangent hyperplane to the (QP) No Compute approximate gradient to the curve using finite difference 27

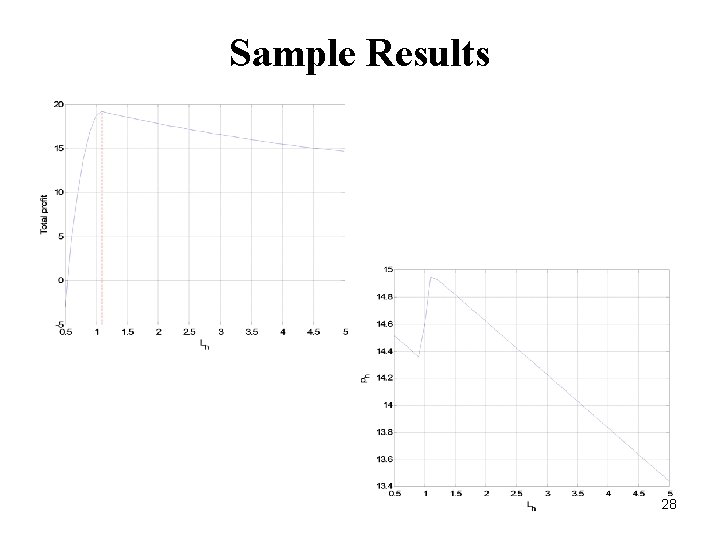
Sample Results 28

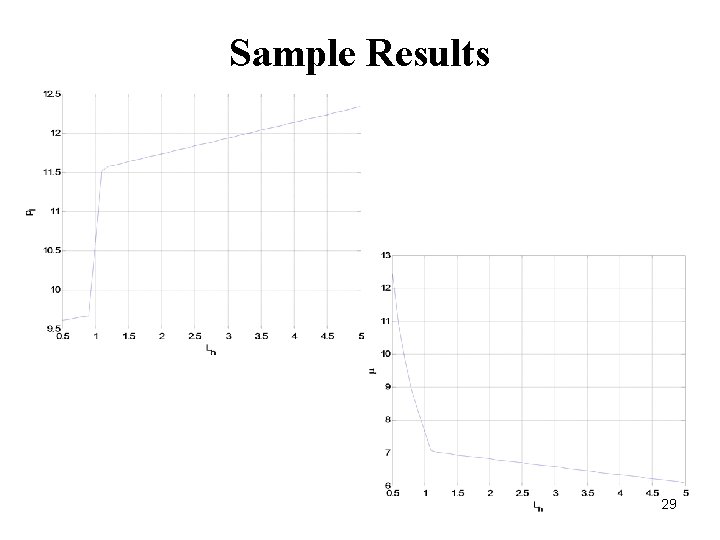
Sample Results 29

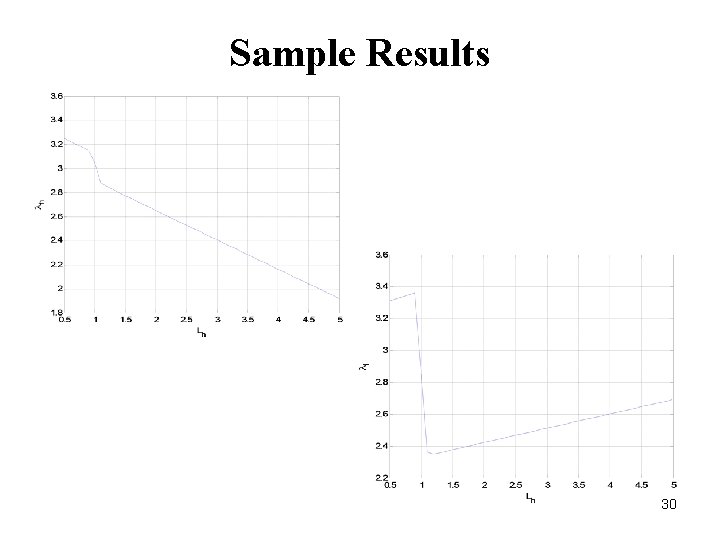
Sample Results 30

Managerial Insights (Future Research) • Impact of L 1 on relative pricing and total profit? • Impact of A on pricing decisions ? • Impact of a shared production capacity on pricing decisions and total profit? • Role of market characteristics (βp, βL, θp, θL) on leadtime and pricing decisions? 31

32