Optimization Unconstrained Minimization Def fx x is said

Optimization 吳育德

Unconstrained Minimization Def : f(x), x is said to be differentiable at a point x*, if it is defined in a neighborhood N around x* and if x* +h a vector n independent of h that where the vector a is called the gradient of f(x) evaluated at x*, denote it as The term <a, h> is called the 1 -st variation. and

Unconstrained Minimization Note if f(x) is twice differentiable, then where F(x) is an n*n symmetric, called the Hessian of f(x) Then 1 st variation 2 nd variation

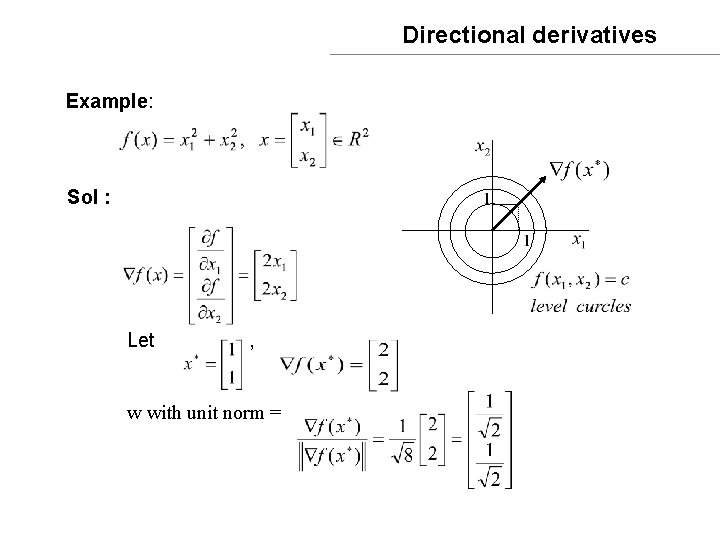
Directional derivatives Let w be a directional vector of unit norm || w|| =1 Now consider is a function of the scalar r. Def : The directional derivative of f(x) in the direction w (unit norm) at w* is defined as

Directional derivatives Example : Let Then i. e. the partial derivative of f(x*) w. r. t xi is the directional derivative of f(x) in the direction ei. Interpretation of Consider Then The directional derivative along a direction w (||w||=1) is the length of the projection vector of on w.

Unconstrained Minimization [Q] : What direction w yield the largest directional derivative? Ans : Recall that the 1 st variation of is Conclusion 1 : The direction of the gradient is the direction that yields the largest change (1 st -variation) in the function. This suggests in the steepest decent method which will be described later

Directional derivatives Example: Sol : Let , w with unit norm =

Directional derivatives The directional derivative in the direction of the gradient is Notes :

Directional derivatives Def : f(x) is said to have a local (or relative) minimum at x*, if in a nbd N of x* Theorem: Let f(x) be differentiable , If f(x) has a local minimum at x* , then pf : Note: is a necessary condition, not sufficient condition.

Directional derivatives Theorem: If f(x) is twice diff and pf : Conclusion 2: The necessary & Sufficient Conditions for a local minimum of f(x) is

Minimization of Unconstrained function Prob. : Let y=f(x) , . We want to generate a sequence and such that it converges to the minimum of f(x). Consider the kth guess, , we can generate provided that we have two of information (1) the direction to go (2) a scalar step size Then Basic descent methods (1) Steepest descent (2) Newton-Raphson method

Steepest Descent Steepest descent : Note 1. a. Optimum it minimizes

Steepest Descent Example :

Steepest Descent Example :

Steepest Descent Optimum iteration Remark : The optimal steepest descent step size can be determined analytically for quadratic function.

Steepest Descent 1. b. other possibilities for choosing (1) Constant step size i. e. adv : simple disadv : no idea of which value of α to choose If α is too large diverge If α is too small very slow (2) Variable step size

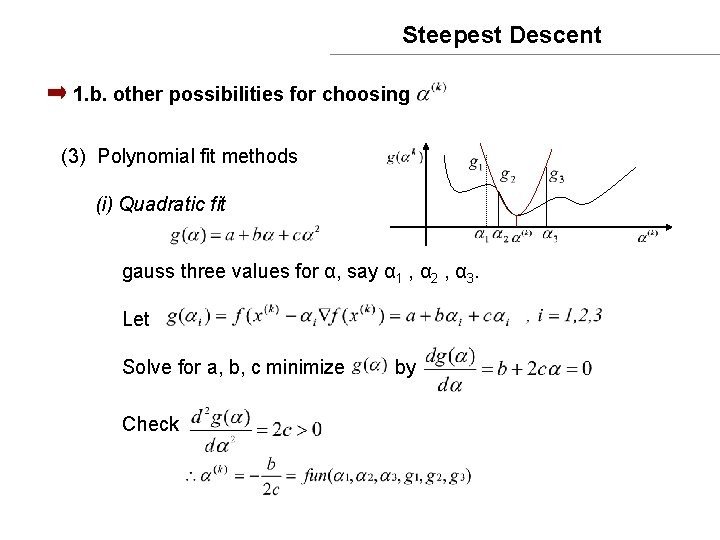
Steepest Descent 1. b. other possibilities for choosing (3) Polynomial fit methods (i) Quadratic fit gauss three values for α, say α 1 , α 2 , α 3. Let Solve for a, b, c minimize by Check

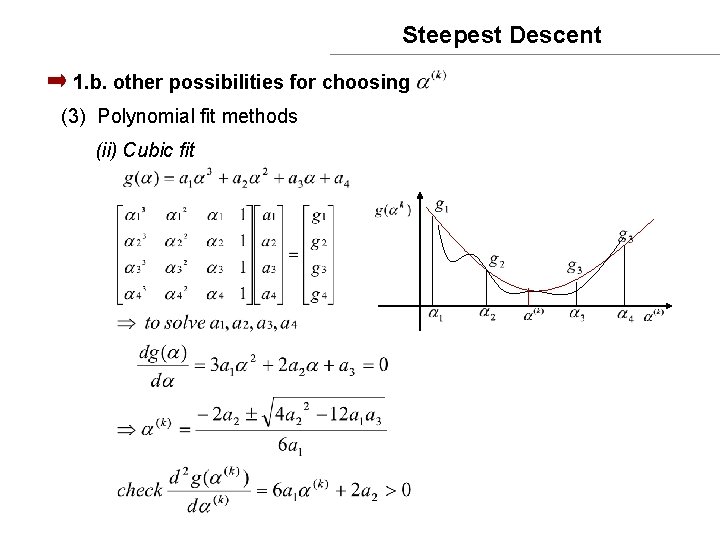
Steepest Descent 1. b. other possibilities for choosing (3) Polynomial fit methods (ii) Cubic fit

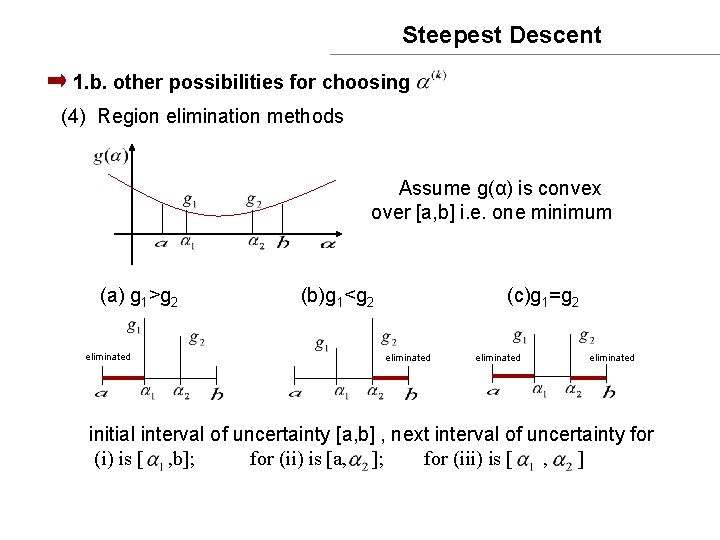
Steepest Descent 1. b. other possibilities for choosing (4) Region elimination methods Assume g(α) is convex over [a, b] i. e. one minimum (a) g 1>g 2 (b)g 1<g 2 (c)g 1=g 2 eliminated initial interval of uncertainty [a, b] , next interval of uncertainty for (i) is [ , b]; for (ii) is [a, ]; for (iii) is [ , ]

Steepest Descent [Q] : how do we choose and ? (i) Two points equal interval search i. e. α 1 - a = α 1 - α 2=b- α 1 1 st iteration 2 nd iteration 3 rd iteration kth iteration

Steepest Descent [Q] : how do we choose and ? (ii) Fibonacci Search method For N-search iteration Example: Let N=5, initial a = 0 , b = 1 k=0

Steepest Descent [Q] : how do we choose and ? (iii) Golden Section Method then use until Example: then etc…

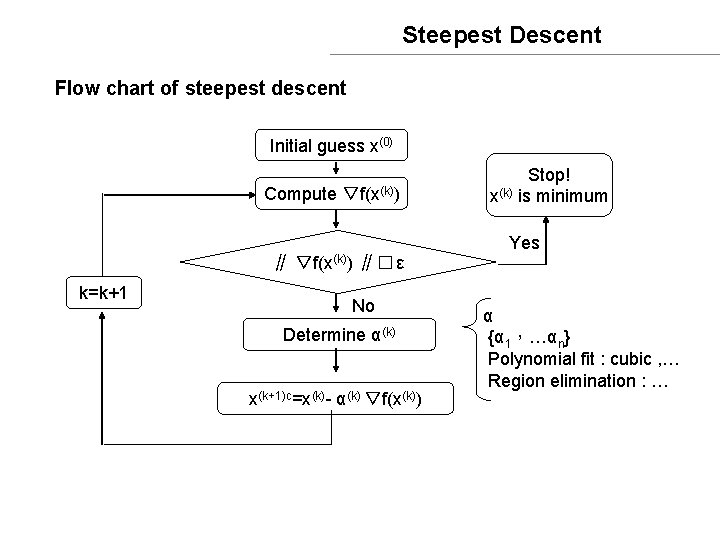
Steepest Descent Flow chart of steepest descent Initial guess x(0) Compute ▽f(x(k)) ∥� ε k=k+1 No Determine α(k) x(k+1)c=x(k)- α(k) ▽f(x(k)) Stop! x(k) is minimum Yes α {α 1，…αn} Polynomial fit : cubic , … Region elimination : …

Steepest Descent [Q]: is the direction of the “best” direction to go? suppose the initial guess is x(0) Consider the next guess What should M be such that x(1) is the minimum, i. e. ? Since we want If MQ=I，or M=Q-1 Thus，for a quadratic function，x(k+1)=x(k)-Q-1▽f(x(k)) will take us to the minimum in one iteration no matter what x(0) is.

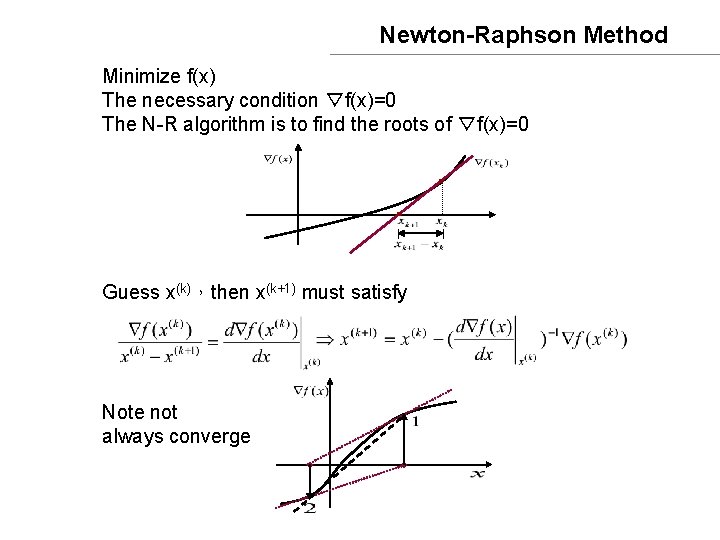
Newton-Raphson Method Minimize f(x) The necessary condition ▽f(x)=0 The N-R algorithm is to find the roots of ▽f(x)=0 Guess x(k)，then x(k+1) must satisfy Note not always converge

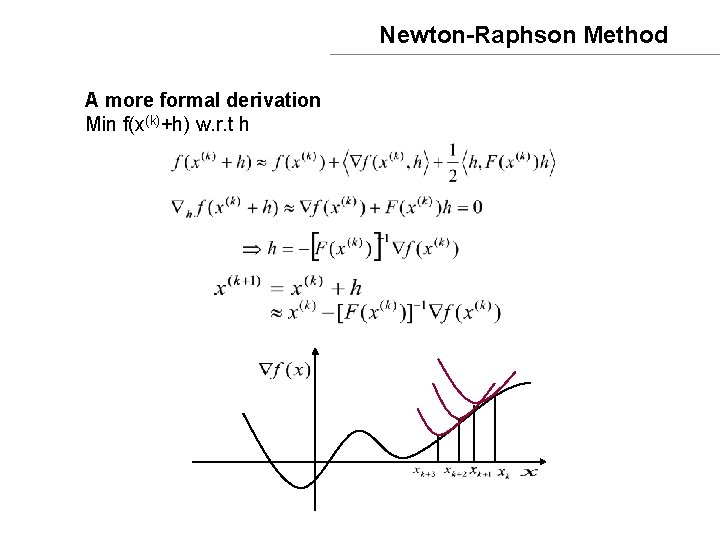
Newton-Raphson Method A more formal derivation Min f(x(k)+h) w. r. t h

Newton-Raphson Method Remarks： （1）computation of [F(x(k))]-1 at every iteration → time consuming → modify N-R algorithm to calculate [F(x(k))]-1 every M-th iteration （2）must check F(x(k)) is p. d. at every iteration. If not → Example ：

Newton-Raphson Method The minimum of f(x) is at (0, 0) In the nbd of (0, 0) is p. d. Now suppose we start an initial guess Then diverges. Remark： （3）N-R algorithm is good(fast) when initial guess close to minimum ，but not very good when far from minimum.