Optimization of Sequential Networks Step in Synthesis We

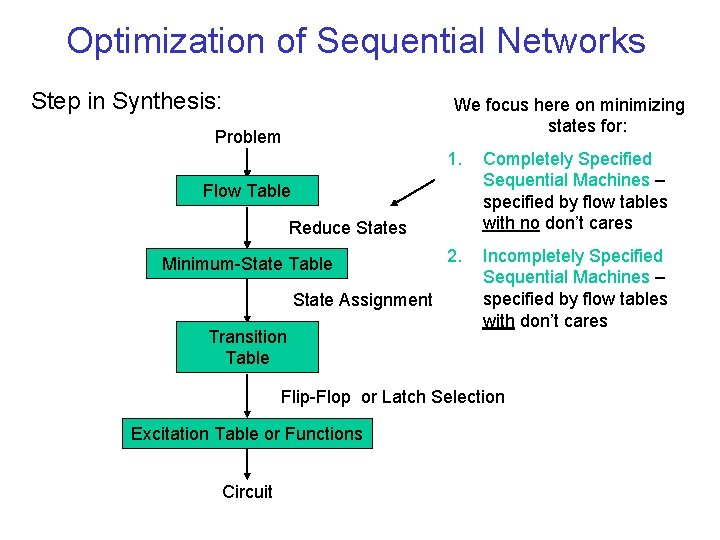
Optimization of Sequential Networks Step in Synthesis: We focus here on minimizing states for: Problem 1. Completely Specified Sequential Machines – specified by flow tables with no don’t cares 2. Incompletely Specified Sequential Machines – specified by flow tables with don’t cares Flow Table Reduce States Minimum-State Table State Assignment Transition Table Flip-Flop or Latch Selection Excitation Table or Functions Circuit

State Reduction Goal Given a flow table, to find an indistinguishable, minimumstate flow table. Note: this leads to a circuit with fewest possible memory elements & usually a minimum cost (but not always) Indistinguishable Flow Tables - flow tables that specify identical output sequences for the same input sequence. Inaccessible States – states not reached from initial state or from desired pattern • We want to eliminate inaccessible states by state reduction or by making them accessible. • We assume this is done before other state reduction techniques are employed.

Table Reduction for Completely Specified Networks Consider two flow tables: Table T Present state Table T* Next state, output x=0 x=1 A B, 1 C, 0 B B, 1 C, 0 C A, 0 D, 1 D A, 0 D, 1 Present state Next state, output x=0 x=1 E E, 1 F, 0 F E, 0 F, 1 If the same input sequence is applied to T or T*, they produce the same output sequences Example: for sequence x = 011, z(T, A)=101, z(T*, E)=101

Distinguishability Two states of a FSM si and sj are distinguishable if they produce different output sequences for the same input sequence. Such an input sequence is a distinguishing sequence of (si, sj) Two states of a FSM si and sj are equivalent or indistinguishable if they produce the same output sequences for the same input sequence and are members of an indistinguishable class. If there is a distinguishing sequence with length k for (si, sj), the (si, sj) is k-distinguishable Goal: to merge all equivalent states to obtain the minimum number of states.

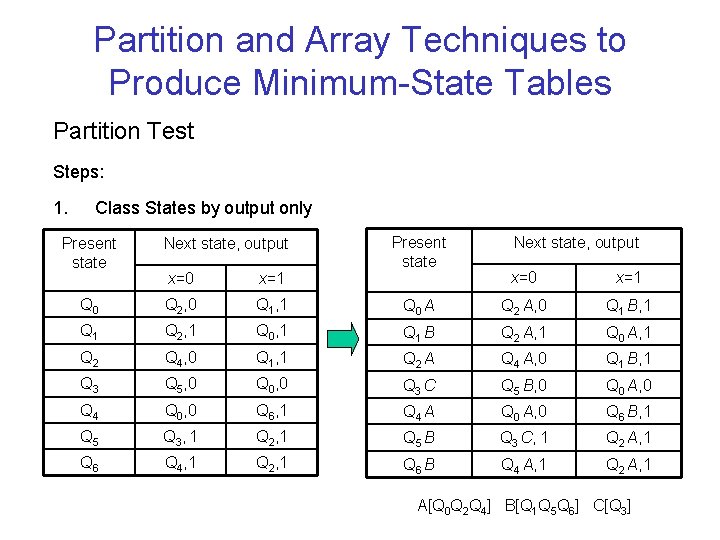
Partition and Array Techniques to Produce Minimum-State Tables Partition Test Steps: 1. Class States by output only Present state Next state, output x=0 x=1 Q 0 A Q 2 A, 0 Q 1 B, 1 Q 0, 1 Q 1 B Q 2 A, 1 Q 0 A, 1 Q 4, 0 Q 1, 1 Q 2 A Q 4 A, 0 Q 1 B, 1 Q 3 Q 5, 0 Q 0, 0 Q 3 C Q 5 B, 0 Q 0 A, 0 Q 4 Q 0, 0 Q 6, 1 Q 4 A Q 0 A, 0 Q 6 B, 1 Q 5 Q 3, 1 Q 2, 1 Q 5 B Q 3 C, 1 Q 2 A, 1 Q 6 Q 4, 1 Q 2, 1 Q 6 B Q 4 A, 1 Q 2 A, 1 x=0 x=1 Q 0 Q 2, 0 Q 1, 1 Q 2, 1 Q 2 A[Q 0 Q 2 Q 4] B[Q 1 Q 5 Q 6] C[Q 3]

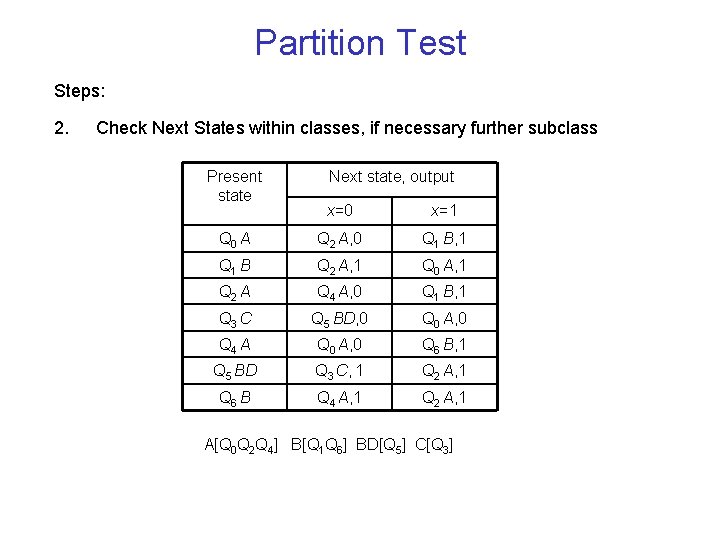
Partition Test Steps: 2. Check Next States within classes, if necessary further subclass Present state Next state, output x=0 x=1 Q 0 A Q 2 A, 0 Q 1 B, 1 Q 1 B Q 2 A, 1 Q 0 A, 1 Q 2 A Q 4 A, 0 Q 1 B, 1 Q 3 C Q 5 BD, 0 Q 0 A, 0 Q 4 A Q 0 A, 0 Q 6 B, 1 Q 5 BD Q 3 C, 1 Q 2 A, 1 Q 6 B Q 4 A, 1 Q 2 A, 1 A[Q 0 Q 2 Q 4] B[Q 1 Q 6] BD[Q 5] C[Q 3]

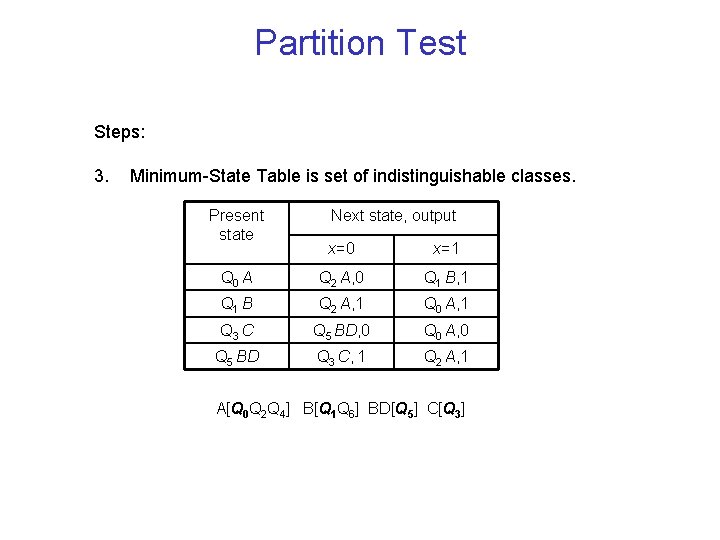
Partition Test Steps: 3. Minimum-State Table is set of indistinguishable classes. Present state Next state, output x=0 x=1 Q 0 A Q 2 A, 0 Q 1 B, 1 Q 1 B Q 2 A, 1 Q 0 A, 1 Q 3 C Q 5 BD, 0 Q 0 A, 0 Q 5 BD Q 3 C, 1 Q 2 A, 1 A[Q 0 Q 2 Q 4] B[Q 1 Q 6] BD[Q 5] C[Q 3]

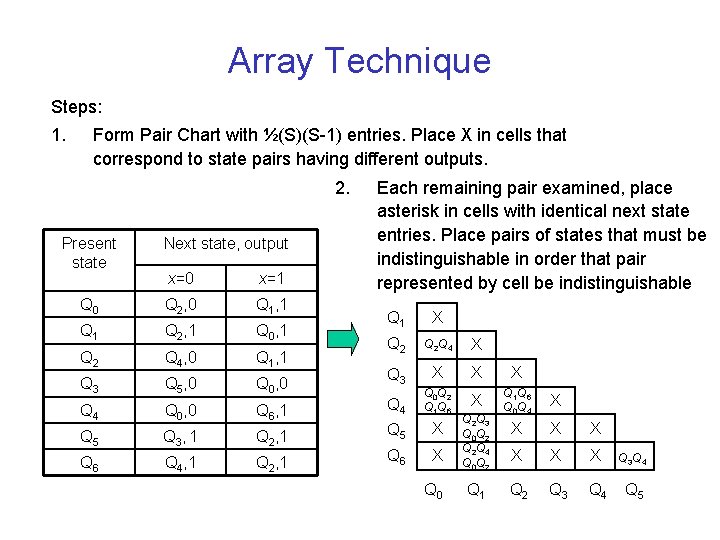
Array Technique Steps: 1. Form Pair Chart with ½(S)(S-1) entries. Place X in cells that correspond to state pairs having different outputs. 2. Present state Next state, output x=0 x=1 Q 0 Q 2, 0 Q 1, 1 Q 2, 1 Q 0, 1 Q 2 Q 4, 0 Q 1, 1 Q 3 Q 5, 0 Q 0, 0 Q 4 Q 0, 0 Q 6, 1 Q 5 Q 3, 1 Q 2, 1 Q 6 Q 4, 1 Q 2, 1 Each remaining pair examined, place asterisk in cells with identical next state entries. Place pairs of states that must be indistinguishable in order that pair represented by cell be indistinguishable Q 1 X Q 2 Q 4 X Q 3 X X X Q 4 Q 0 Q 2 Q 1 Q 6 X Q 1 Q 6 Q 0 Q 4 X Q 5 X X Q 6 X X Q 3 Q 4 Q 2 Q 3 Q 4 Q 5 Q 0 Q 2 Q 3 Q 0 Q 2 Q 2 Q 4 Q 0 Q 2 Q 1

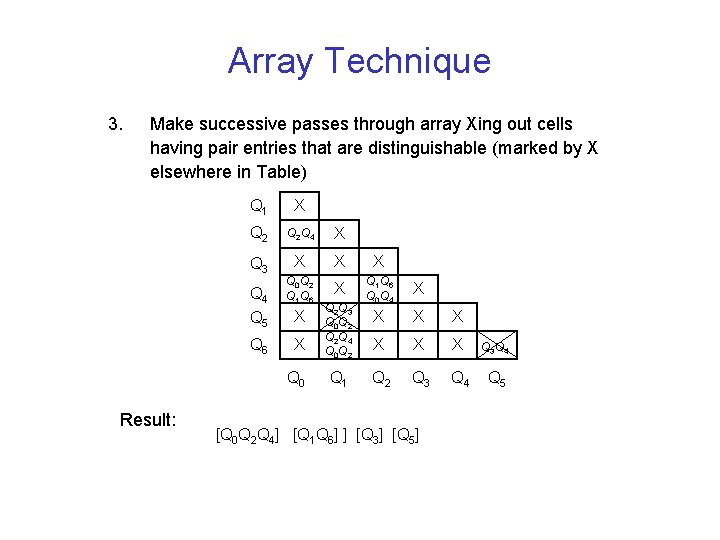
Array Technique 3. Make successive passes through array Xing out cells having pair entries that are distinguishable (marked by X elsewhere in Table) Q 1 X Q 2 Q 4 X Q 3 X X X Q 4 Q 0 Q 2 Q 1 Q 6 X Q 1 Q 6 Q 0 Q 4 X Q 5 X X Q 6 X X Q 3 Q 4 Q 2 Q 3 Q 4 Q 5 Q 0 Result: Q 2 Q 3 Q 0 Q 2 Q 2 Q 4 Q 0 Q 2 Q 1 [Q 0 Q 2 Q 4] [Q 1 Q 6] ] [Q 3] [Q 5]

Optimization of Incompletely Specified Machines Some definitions: Two states are I-Equivalent IFF 1. Outputs are identical, if specified 2. Matching d-outputs occur 3. Matching unspecified next states occur or specified next states must be equivalent. Two states are Compatible IFF 1. Outputs are identical, if specified 2. Compatible next-states occur, if both are specified. Maximal Compatible Classes - classes that are not subsets of any other compatibility class.

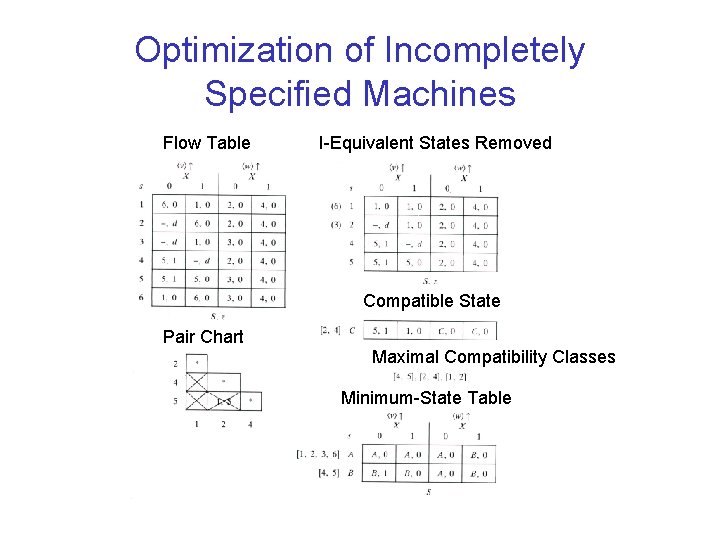
Optimization of Incompletely Specified Machines Flow Table I-Equivalent States Removed Compatible State Pair Chart Maximal Compatibility Classes Minimum-State Table

Optimization of Incompletely Specified Machines Steps in finding Reduced Table: 1. Remove I-Equivalence states 2. Find Maximal Compatibility Classes 3. Form Flow Table in which each state corresponds to a maximal compatibility class subject to satisfying the closure property and all states of the original table are represented, that is satisfying the covering property.

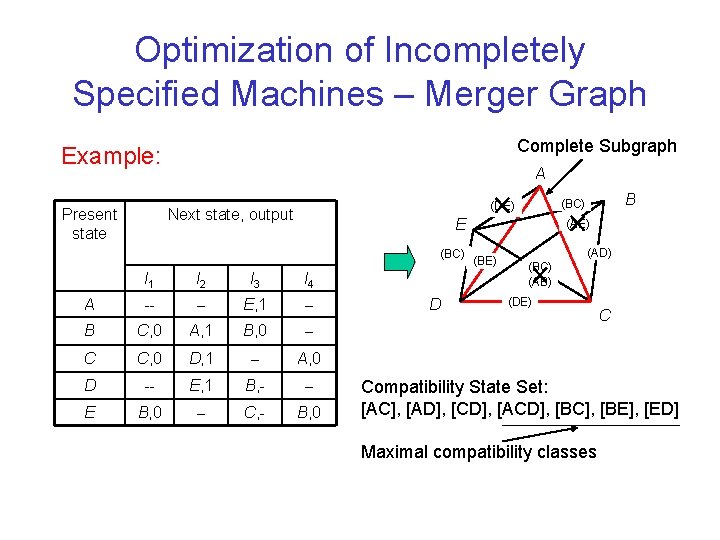
Optimization of Incompletely Specified Machines – Array Technique Example: Present state A Next state, output B X C * AD AE I 1 I 2 I 3 I 4 -- -- E, 1 -- D BE E CE BC AB. B C, 0 A, 1 B, 0 -- C C, 0 D, 1 -- A, 0 D -- E, 1 B, - -- E B, 0 -- C, - B, 0 DE BC A B C BC D Compatibility State Set: [AC], [AD], [CD], [ACD], [BC], [BE], [ED] Maximal compatibility classes

Optimization of Incompletely Specified Machines – Merger Graph Complete Subgraph Example: Present state A Next state, output E (BC) I 1 I 2 I 3 I 4 A -- -- E, 1 -- B C, 0 A, 1 B, 0 -- C C, 0 D, 1 -- A, 0 D -- E, 1 B, - -- E B, 0 -- C, - B, 0 D B (BC) (DE) (AE) (BE) (AD) (BC) (AB) (DE) C Compatibility State Set: [AC], [AD], [CD], [ACD], [BC], [BE], [ED] Maximal compatibility classes

State Compatibility Graph is a directed graph satisfying the conditions: 1. Each node corresponds to a compatible state set. 2. When a state set implies another state set S, attach OR directed edges from the nodes corresponding to the original state set to the node corresponding to the state sets containing S. 3. When a state set implies two or more state sets: S 0, …. , Sk -1, Sk, Attach AND directed edges from the node corresponding to the original state set to the nodes that correspond to S 0, …. , S k-1, Sk

Finding Minimum Number of States Using State Compatibility Graph Must Satisfy Two Conditions: 1. Covering Property – Each state of the FSM is contained by at least one compatible set V 2. Closure Property: If vi V, then Vi V, where Vi is the set of implied compatible sets. Vi satisfies the following condition: for the OR directed edges that emerge from vi , Vi contains the nodes for at least one edge. For the AND directed edges that emerge from vi , Vi contains the nodes for all the AND directed edges.

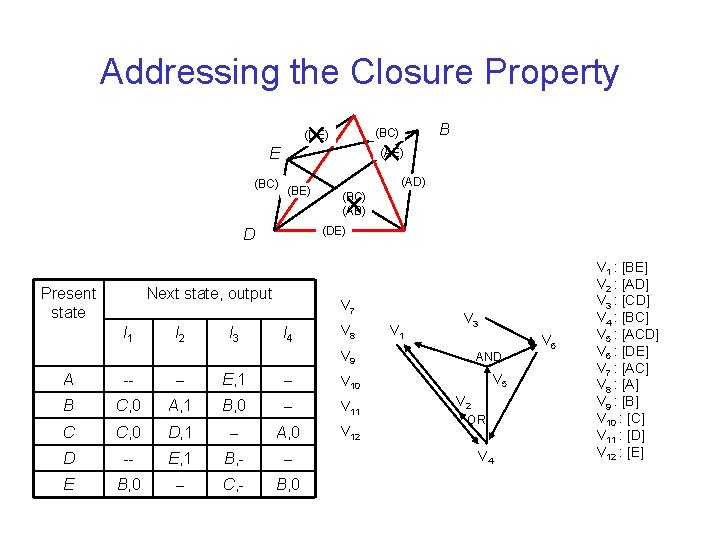
Addressing the Closure Property E (BC) (AE) (BE) Next state, output I 1 I 2 I 3 (AD) (BC) (AB) (DE) D Present state B (BC) (DE) V 7 I 4 V 8 V 1 V 3 V 9 A -- -- E, 1 -- V 10 B C, 0 A, 1 B, 0 -- V 11 C C, 0 D, 1 -- A, 0 V 12 D -- E, 1 B, - -- E B, 0 -- C, - B, 0 AND V 5 V 2 OR V 4 V 6 V 1 : [BE] V 2 : [AD] V 3 : [CD] V 4 : [BC] V 5 : [ACD] V 6 : [DE] V 7 : [AC] V 8 : [A] V 9 : [B] V 10 : [C] V 11 : [D] V 12 : [E]

Optimization Example Covering Property State A: v 2 + v 5 + v 7 + v 8 = 1 State B: v 1 + v 4 + v 9 = 1 State C: v 3 + v 4 + v 5 + v 7 + v 10 = 1 State D: v 2 + v 3 + v 5 + v 6 + v 11 = 1 State E: v 1 + v 6 + v 12 = 1

Closure Property Example From the state compatibility graph v 1 v 4 , so v 1 + v 4 = 1 v 2 v 1 , so v 2 + v 1 = 1 v 3 v 6 , so v 3 + v 6 = 1 v 4 (v 2 + v 5 ), so v 4 + v 2 + v 5 = 1 v 5 v 1 v 6, so (v 5 + v 1 )(v 5 + v 6) = 1 v 6 v 4 , so v 6 + v 4 = 1 AND of all conditions gives solution of minimum weight