Optimization of Multilevel Checkpoint Model for Large Scale

Optimization of Multi-level Checkpoint Model for Large Scale HPC Applications Sheng Di, Mohamed Slim Bouguerra, Leonardo Bautista-gomez, Franck Cappello INRIA and ANL 2013 1

Outline Background of Multi-level Checkpoint Model Problem Formulation Optimization of Multi-level Checkpoint Model Optimizing Checkpoint Intervals for each level Optimizing the Selection of Levels Performance Evaluation Conclusion and Future Work 2

Background of Multi-level Ckpt Model Traditional Ckpt/Restart model always stores checkpoint files onto Parallel File System (PFS) PFS is of central-controlled mode, which suffers bottle-neck issue for large-scale app. For example, our experiments shows that the checkpoint overhead on PFS increases quickly with problem size and execution scale: # cores 128 256 512 1024 Ckpt cost 7. 4 sec 10. 8 sec 16. 8 sec 43. 1 sec 3

Background of Multi-level Ckpt Model Existing Multi-level checkpoint toolkits Scalable Checkpoint/Restart Library (SCR) – SC’ 10 RAM disk / local disk Partner-copy / XOR encoding Parallel File System (PFS), e. g. , NFS Fault Tolerance Interface (FTI) - SC’ 11 Local disk: storing ckpt files into local disk Partner-copy: storing ckpt files in local disk & partner disk Reed-Solomon encoding (RS-encoding) 4 Parallel File System (PFS): such as NFS

Problem Formulation Different Types of Failures CPL 1: There are no hardware failures but software errors. CPL 2: There are non-adjacent hardware failures CPL 3: There a few adjacent hardware failures CPL 4: There a lot of hardware failures 5

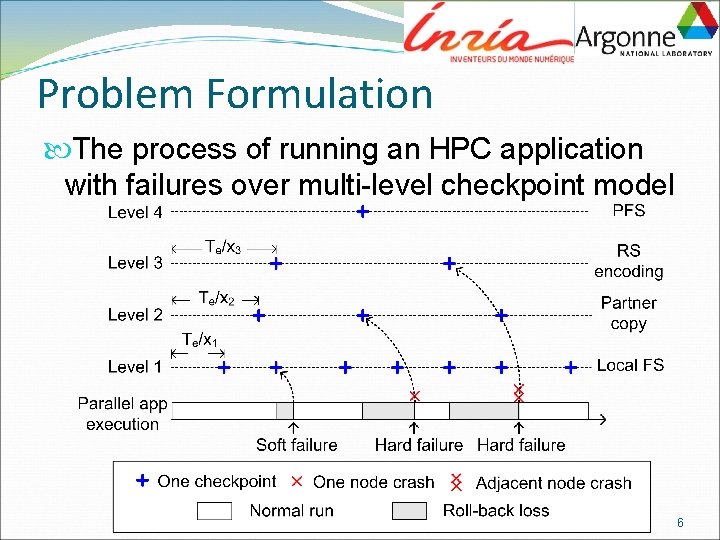
Problem Formulation The process of running an HPC application with failures over multi-level checkpoint model 6

Problem Formulation Our Objective - Minimize the expected wallclock length for each HPC application with: # of levels optimized selection of levels Productive time # of ckpt intervals at level i optimized checkpoint intervals on each level Mathematical Expectation of Wall-clock Length: # of failures at level i probability Ckpt overhead Rollback loss Restart cost 7

Optimization of Multi-level Checkpoint Model E(Tw) is convex, because xi is referred to as the # of ckpt intervals at level i We get optimal solution as long as we solve the simultaneous equations, optimal xi* : where i = 1, 2, 3, …. , L 8

Optimization of Multi-level Checkpoint Model Optimizing Checkpoint Intervals Simplified equations: We use an iterative algorithm to solve it: k=0: err=0. 2 k=1: err=0. 08 k+1 k=2: err=0. 005 K=3: err=0. 0001 …… We use Young’s formula k k to initialize xi(0) 9

Optimization of Multi-level Checkpoint Model Optimizing Checkpoint Intervals How fast is our iterative optimal algorithm? If we set the error threshold to 10 -6, the algorithm will converge with only about 20 -30 iterations !! What is the performance gain under our method, compared to the traditional Young’s formula? Suppose there are 8 levels and application execution length is 1000 ~ 9000 seconds The checkpoint overheads on the 8 levels are 10, 30, 45, 50, 55, 60, 65, 240 seconds per checkpoint. Numerical simulation shows that our method is better than Young’s formula by 4. 2% - 17. 8%. 10

Optimization of Multi-level Checkpoint Model Optimizing Selection of Checkpoint Levels For a particular combination of levels, the computation complexity is only about 30 iterations. It is feasible to traverse all of combinations of levels to find the optimal selection of levels. Suppose there are 8 levels, so there are 281=255 different combinations of levels, and the total computation complexity is 255*30=7650, which is very small! 11

Optimization of Multi-level Checkpoint Model Analysis of A Practical Case – FTI There are 4 levels: local disk, partner-copy, RS- encoding, and PFS Use Clf, Cpc, Crs, Cpf to denote ckpt overheads Use Rlf, Rpc, Rrs, Rpf to denote restart overheads 12

Optimization of Multi-level Checkpoint Model Analysis of A Practical Case – FTI The target simultaneous equations derived from convex optimization (first-order derivatives) is: The solution to the above equations must be optimal We can use iterative method to get it very quickly. 13

Performance Evaluation Experimental Setting Evaluation Type A: Numerical Simulation To evaluate a large number of various cases with different parameters, including different ckpt overheads, restart cost, application length, etc. Evaluation Type B: Real Experiment To validate the feasibility of using our optimal checkpoint model in a real use case – FTI scenario. MPI program used in our experiment: Head distribution 14

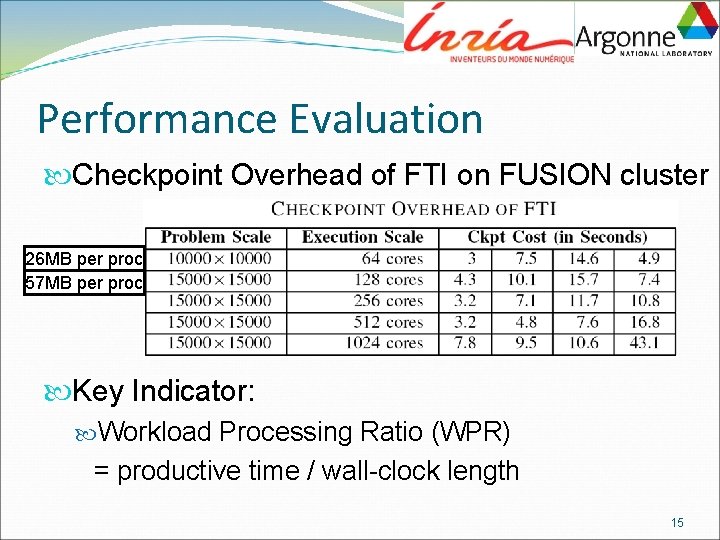
Performance Evaluation Checkpoint Overhead of FTI on FUSION cluster 26 MB per proc 57 MB per proc Key Indicator: Workload Processing Ratio (WPR) = productive time / wall-clock length 15

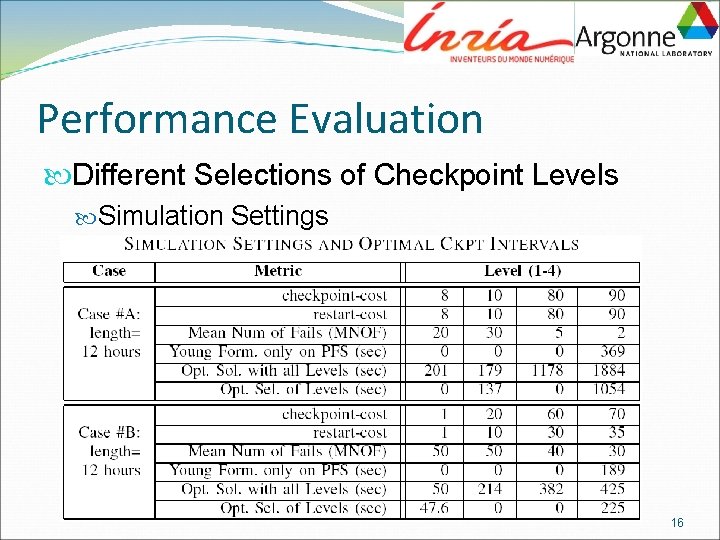
Performance Evaluation Different Selections of Checkpoint Levels Simulation Settings 16

Performance Evaluation Different Selections of Checkpoint Levels Simulation Results Improvement: 10 -20% 17

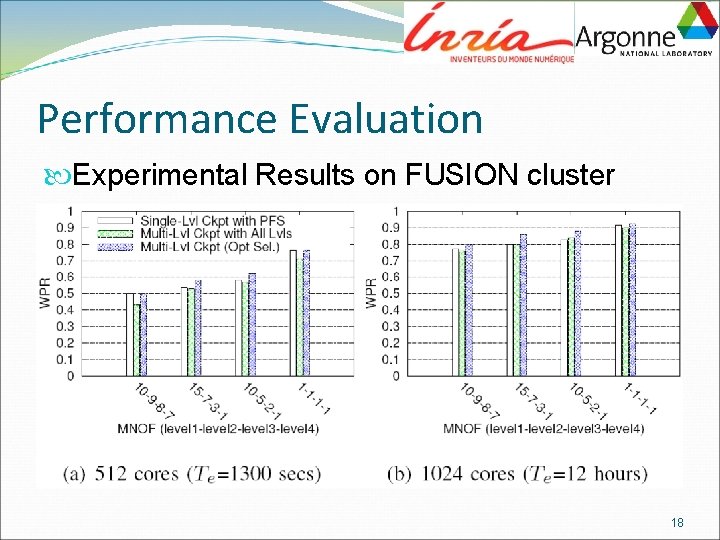
Performance Evaluation Experimental Results on FUSION cluster 18

Conclusion Optimal Multi-level Checkpoint/Restart Model Key Theoretical Conclusions: Ckpt intervals on each level can be optimized by fast iterative methods (converged within only 30 iterations) The ckpt intervals are optimal based on convexoptimization theory Key Simulation/Experimental Results: For FTI, Iterative Optimal method with best selection of levels is better than other solutions by up to 20%. For other cases like 8 levels, Optimized selection of levels can improve performance by 50% in some cases. 19

Future Work In the future, we plan to: evaluate our optimal ckpt/restart model using more complex MPI program on real clusters with larger scales, such as CESM. optimize the robustness and stability by taking into account the possible prediction errors on checkpoint overheads and execution length. optimize the execution scale (# of processes) based on checkpoint overheads for some application with specific productive time. 20

Thanks!! Contact me at: disheng 222@gmail. com 21