Optimization of Multibody Systems JeanFranois Collard Paul Fisette

Optimization of Multibody Systems Jean-François Collard Paul Fisette 24 May 2006

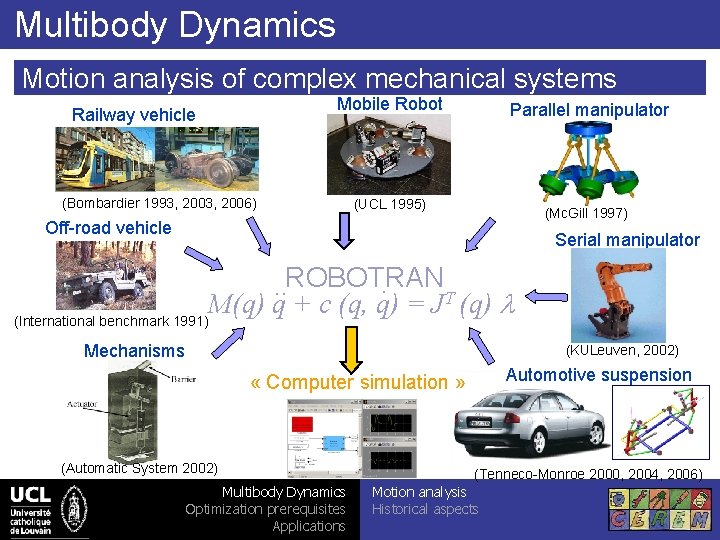
Multibody Dynamics Motion analysis of complex mechanical systems Mobile Robot Railway vehicle (Bombardier 1993, 2006) Parallel manipulator (UCL 1995) (Mc. Gill 1997) Off-road vehicle Serial manipulator . . . ROBOTRAN T (q) l M(q) q + c (q, q) = J (International benchmark 1991) Mechanisms (KULeuven, 2002) Automotive suspension « Computer simulation » (Automatic System 2002) Multibody Dynamics Optimization prerequisites Applications (Tenneco-Monroe 2000, 2004, 2006) Motion analysis Historical aspects

Multibody Dynamics Historical aspects n 1970 … Satellites : “first” multibody applications ¨ Analytical linear model – Modal analyses ¨ n 1980 … Vehicle dynamics, Robotics (serial robots) ¨ “Small” nonlinear models, Time simulation of “small systems” ¨ n 1990 … Vehicle, machines, helicopters, mechanisms, human body, etc. ¨ Flexible elements, Non-linear simulations, Sensitivity analysis, … ¨ n 2000 … Idem + Multiphysics models (hydraulic circuits, electrical actuator, …) ¨ Idem + Optimization of performances ¨ Multibody Dynamics Optimization prerequisites Applications Motion analysis Historical aspects

Optimization : “prerequisites” n n n Model formulation : assembling, equations of motion ¨ Assembling ¨ Equations of motion Model “fast” simulation ¨ Compact analytical formulation ¨ Compact symbolical implementation (UCL) Model portability ¨ Analytical “ingredients” ¨ Model exportation Multibody Dynamics Optimization prerequisites Applications Model formulation Model « fast » simulation Model portability

Optimization : “prerequisites” Model formulation n Assembling : nonlinear constraint equations : h(q, t) = 0 n Equations of motion « DAE » Reduction technique (UCL) « ODE » Multibody Dynamics Optimization prerequisites Applications Model formulation Model « fast » simulation Model portability

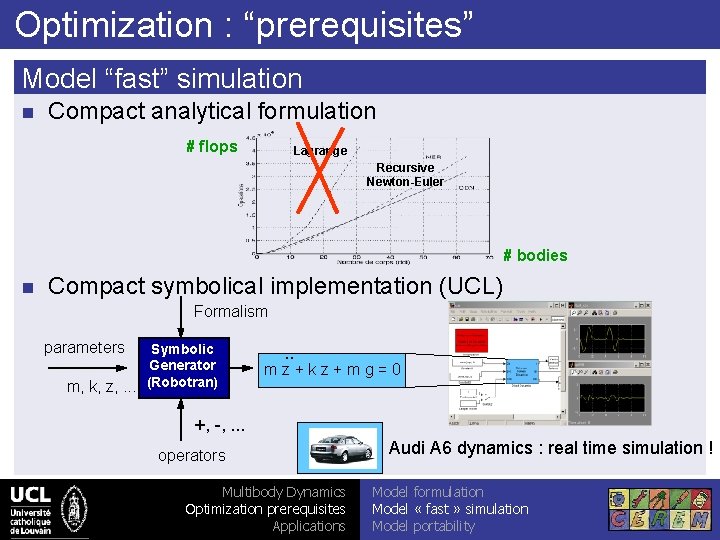
Optimization : “prerequisites” Model “fast” simulation n Compact analytical formulation # flops Lagrange Recursive Newton-Euler # bodies n Compact symbolical implementation (UCL) Formalism parameters Symbolic Generator m, k, z, . . . (Robotran) . . m z + k z + m g = 0 +, -, . . . operators Multibody Dynamics Optimization prerequisites Applications Audi A 6 dynamics : real time simulation ! Model formulation Model « fast » simulation Model portability

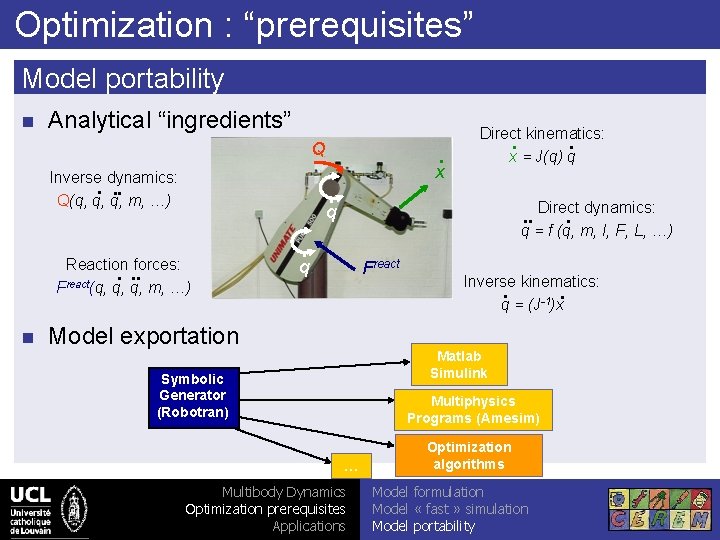
Optimization : “prerequisites” Model portability n Analytical “ingredients” Q Inverse dynamics: . . . Q(q, q, q, m, …) . q Reaction forces: . . . react F (q, q, q, m, …) n . x Direct kinematics: . . x = J(q) q Direct dynamics: . q = f (q, m, I, F, L, …) . . . q Freact Model exportation Inverse kinematics: . . q = (J-1)x Matlab Simulink Symbolic Generator (Robotran) Multiphysics Programs (Amesim) … Multibody Dynamics Optimization prerequisites Applications Optimization algorithms Model formulation Model « fast » simulation Model portability

Optimization: applications n Isotropy of parallel manipulators ¨ n Comfort of road vehicles ¨ n Multi-physics model Biomechanics of motion ¨ n Assembling constraints and penalty method Identification of kinematic and dynamical models Synthesis of mechanisms ¨ Extensible-link approach ¨ Multiple local optima Multibody Dynamics Optimization prerequisites Applications Isotropy of manipulators Comfort of vehicles Biomechanics of motion Synthesis of mechanisms

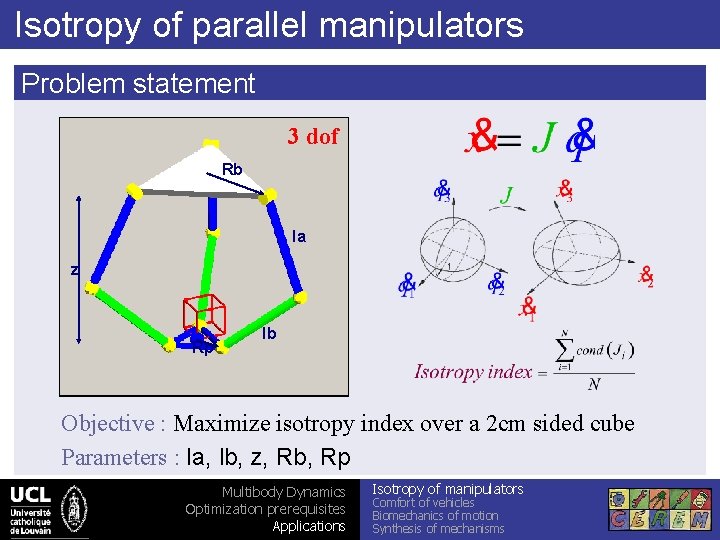
Isotropy of parallel manipulators Problem statement dof 33 dof Rb la z Rp lb Objective : Maximize isotropy index over a 2 cm sided cube Parameters : la, lb, z, Rb, Rp Multibody Dynamics Optimization prerequisites Applications Isotropy of manipulators Comfort of vehicles Biomechanics of motion Synthesis of mechanisms

Isotropy of parallel manipulators Dealing with assembling constraints Constraints involving joint variables q : h(q) = 0 h(q) vq 12 q 1 u Coordinate partitioning : q = [u v] vq 23 Newton-Raphson iterative algorithm: vi+1 = vi – [ h/ v]-1 h(q) Types of problems encountered : u ? h(q) 0 v h/ v = 0 v 1 h(q) = 0 v ? Multiple closed loops u v 1 v 2 u Singularity Multibody Dynamics Optimization prerequisites Applications Isotropy of manipulators Comfort of vehicles Biomechanics of motion Synthesis of mechanisms v 2 Unclosable

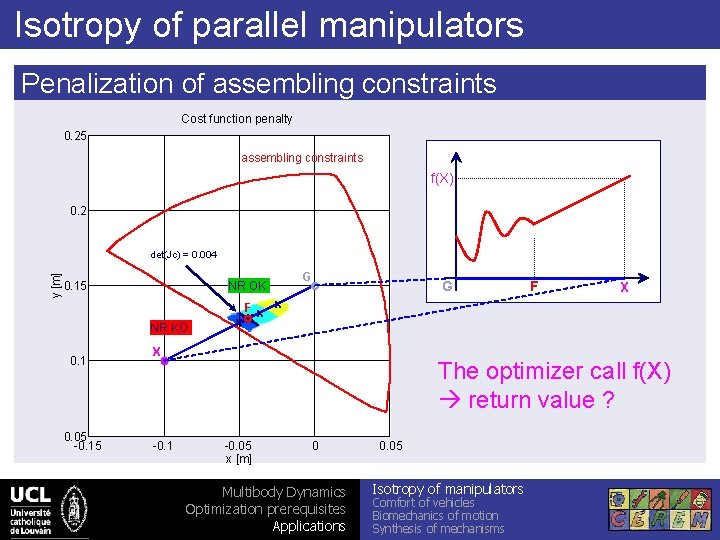
Isotropy of parallel manipulators Penalization of assembling constraints Cost function penalty 0. 25 assembling constraints f(X) 0. 2 y [m] det(Jc) = 0. 004 0. 15 NR OK NR KO 0. 1 0. 05 -0. 15 G G X Fx x xxx X -0. 1 F The optimizer call f(X) return value ? -0. 05 x [m] 0 Multibody Dynamics Optimization prerequisites Applications 0. 05 Isotropy of manipulators Comfort of vehicles Biomechanics of motion Synthesis of mechanisms

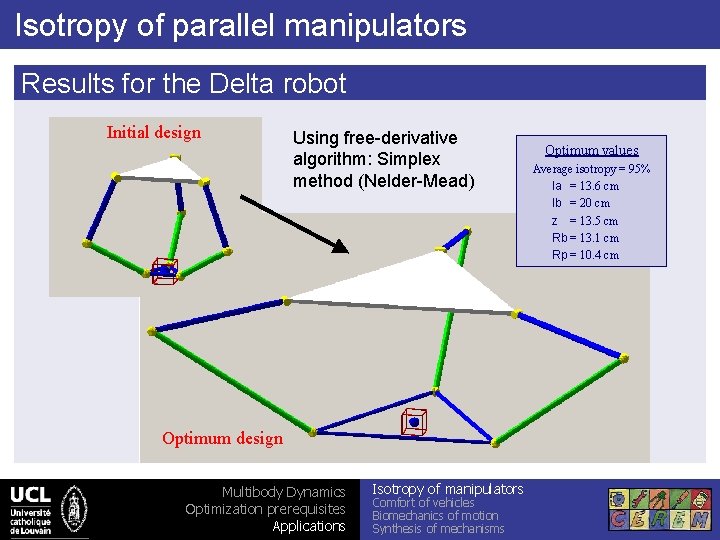
Isotropy of parallel manipulators Results for the Delta robot Initial design Using free-derivative algorithm: Simplex method (Nelder-Mead) Optimum design Multibody Dynamics Optimization prerequisites Applications Isotropy of manipulators Comfort of vehicles Biomechanics of motion Synthesis of mechanisms Optimum values Average isotropy = 95% la = 13. 6 cm lb = 20 cm z = 13. 5 cm Rb = 13. 1 cm Rp = 10. 4 cm

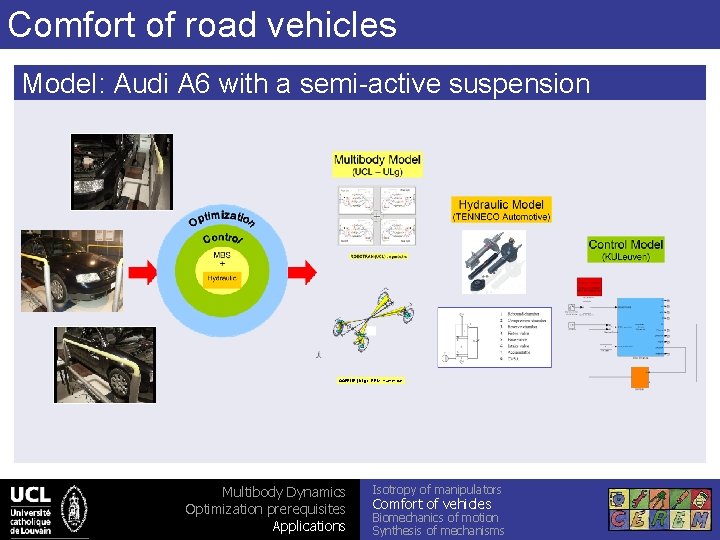
Comfort of road vehicles Model: Audi A 6 with a semi-active suspension OOFELIE (ULg) : FEM - numerical Multibody Dynamics Optimization prerequisites Applications Isotropy of manipulators Comfort of vehicles Biomechanics of motion Synthesis of mechanisms

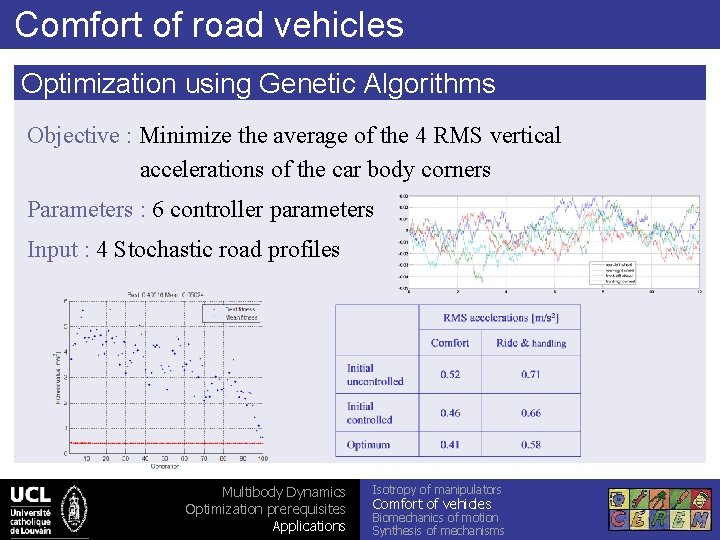
Comfort of road vehicles Optimization using Genetic Algorithms Objective : Minimize the average of the 4 RMS vertical accelerations of the car body corners Parameters : 6 controller parameters Input : 4 Stochastic road profiles Multibody Dynamics Optimization prerequisites Applications Isotropy of manipulators Comfort of vehicles Biomechanics of motion Synthesis of mechanisms

Biomechanics of motion Objective : Quantification of joint and muscle efforts + Electro. Myo. Graphy (EMG) : Fully equipped subject : Multibody Dynamics Optimization prerequisites Applications Isotropy of manipulators Comfort of vehicles Biomechanics of motion Synthesis of mechanisms

Biomechanics of motion Kinematics optimization xmod and xexp superimposed : • MAX relative error = 2. 05 % • MEAN relative error = 0. 05 % MEAN absolute error = 3. 1 mm Multibody Dynamics Optimization prerequisites Applications Isotropy of manipulators Comfort of vehicles Biomechanics of motion Synthesis of mechanisms

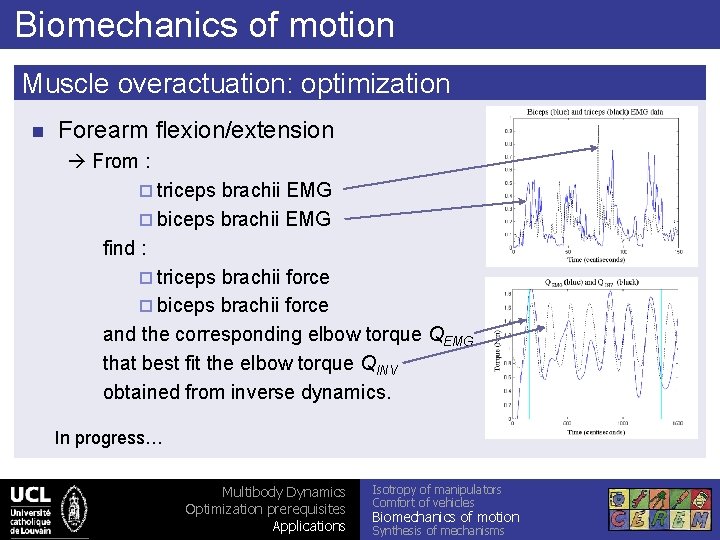
Biomechanics of motion Muscle overactuation: optimization n Forearm flexion/extension From : ¨ triceps brachii EMG ¨ biceps brachii EMG find : ¨ triceps brachii force ¨ biceps brachii force and the corresponding elbow torque QEMG that best fit the elbow torque QINV obtained from inverse dynamics. In progress… Multibody Dynamics Optimization prerequisites Applications Isotropy of manipulators Comfort of vehicles Biomechanics of motion Synthesis of mechanisms

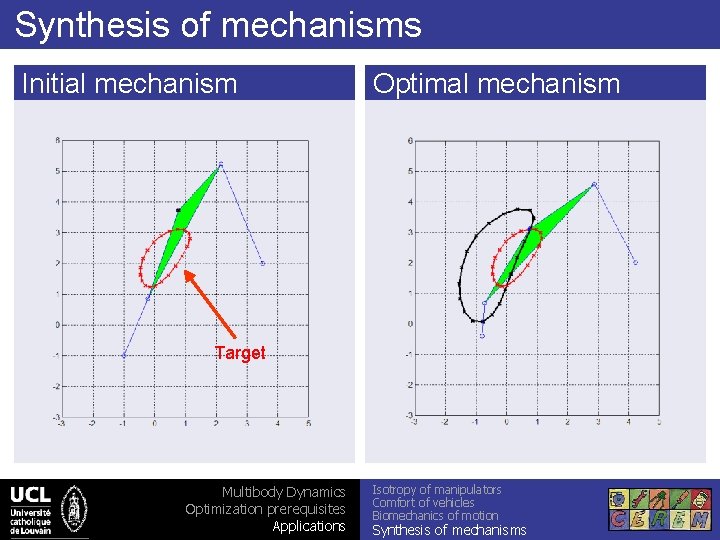
Synthesis of mechanisms Initial mechanism Optimal mechanism Target Multibody Dynamics Optimization prerequisites Applications Isotropy of manipulators Comfort of vehicles Biomechanics of motion Synthesis of mechanisms

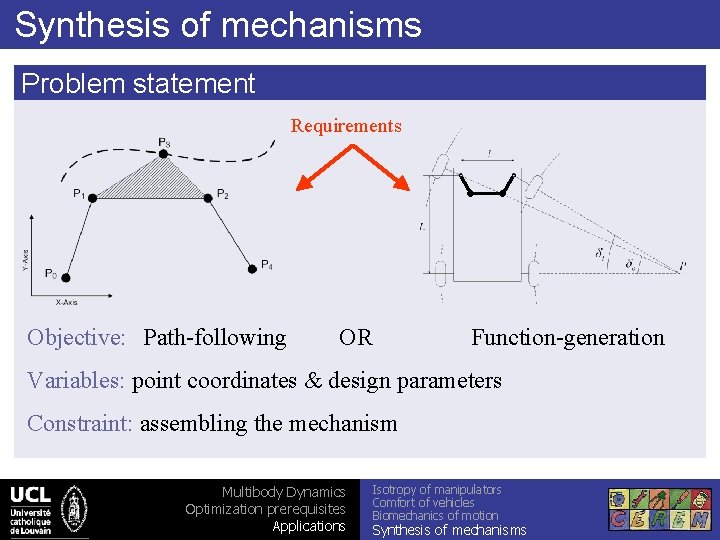
Synthesis of mechanisms Problem statement Objective: Path-following Requirements OR Function-generation Variables: point coordinates & design parameters Constraint: assembling the mechanism Multibody Dynamics Optimization prerequisites Applications Isotropy of manipulators Comfort of vehicles Biomechanics of motion Synthesis of mechanisms

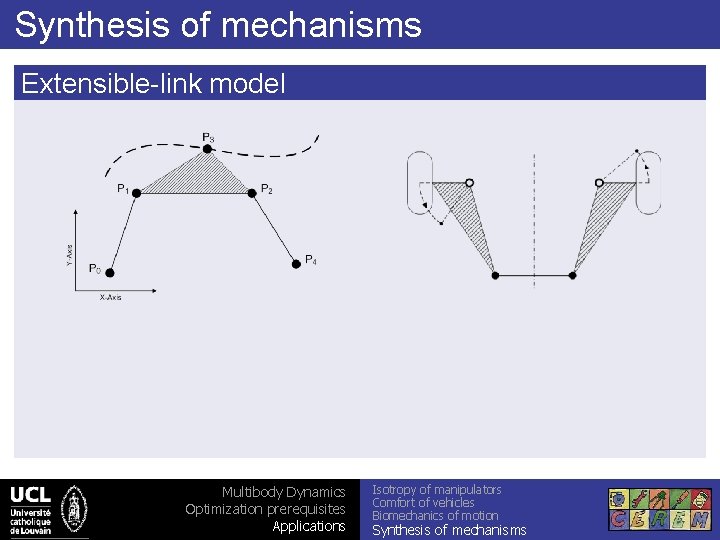
Synthesis of mechanisms Extensible-link model Multibody Dynamics Optimization prerequisites Applications Isotropy of manipulators Comfort of vehicles Biomechanics of motion Synthesis of mechanisms

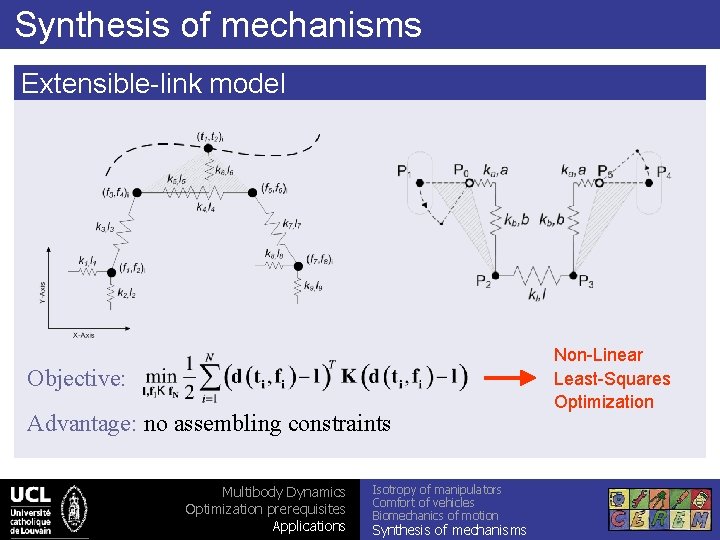
Synthesis of mechanisms Extensible-link model Objective: Advantage: no assembling constraints Multibody Dynamics Optimization prerequisites Applications Isotropy of manipulators Comfort of vehicles Biomechanics of motion Synthesis of mechanisms Non-Linear Least-Squares Optimization

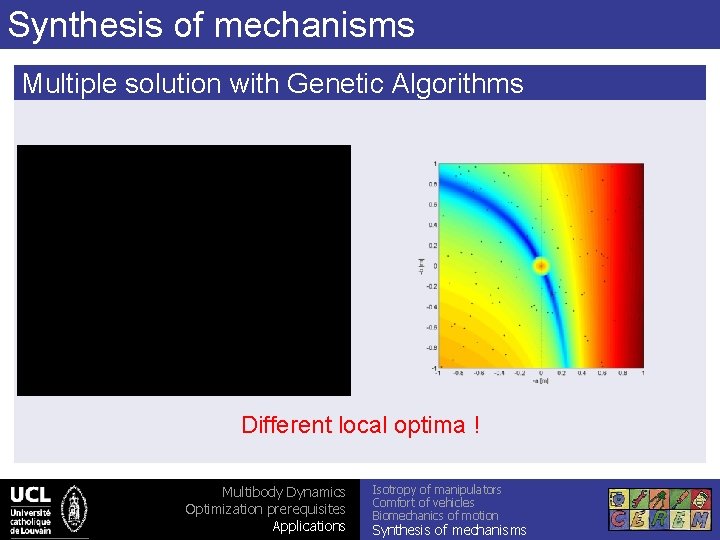
Synthesis of mechanisms Multiple solution with Genetic Algorithms Different local optima ! Multibody Dynamics Optimization prerequisites Applications Isotropy of manipulators Comfort of vehicles Biomechanics of motion Synthesis of mechanisms

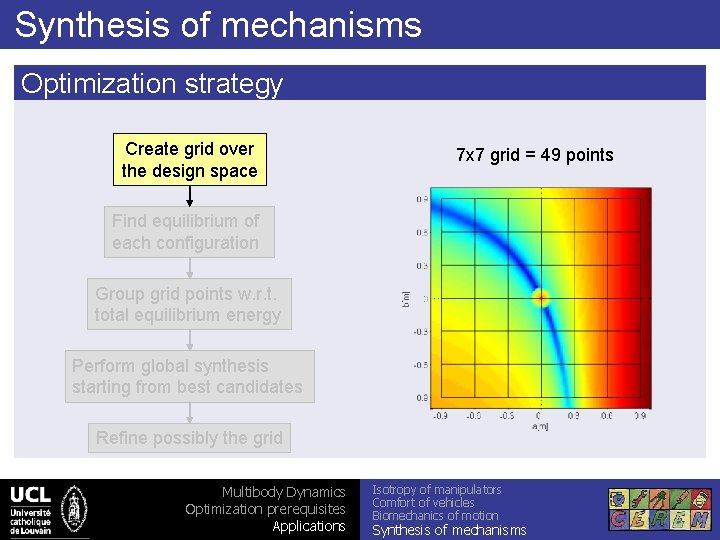
Synthesis of mechanisms Optimization strategy Create grid over the design space 7 x 7 grid = 49 points Find equilibrium of each configuration Group grid points w. r. t. total equilibrium energy Perform global synthesis starting from best candidates Refine possibly the grid Multibody Dynamics Optimization prerequisites Applications Isotropy of manipulators Comfort of vehicles Biomechanics of motion Synthesis of mechanisms

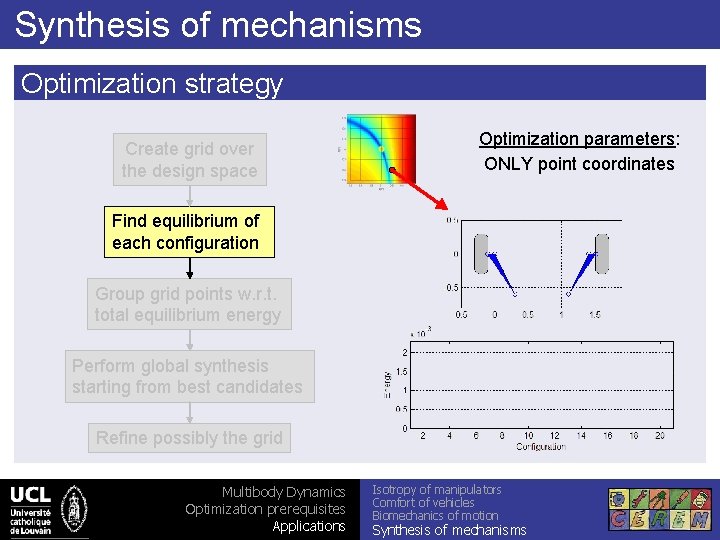
Synthesis of mechanisms Optimization strategy Create grid over the design space Optimization parameters: ONLY point coordinates Find equilibrium of each configuration Group grid points w. r. t. total equilibrium energy Perform global synthesis starting from best candidates Refine possibly the grid Multibody Dynamics Optimization prerequisites Applications Isotropy of manipulators Comfort of vehicles Biomechanics of motion Synthesis of mechanisms

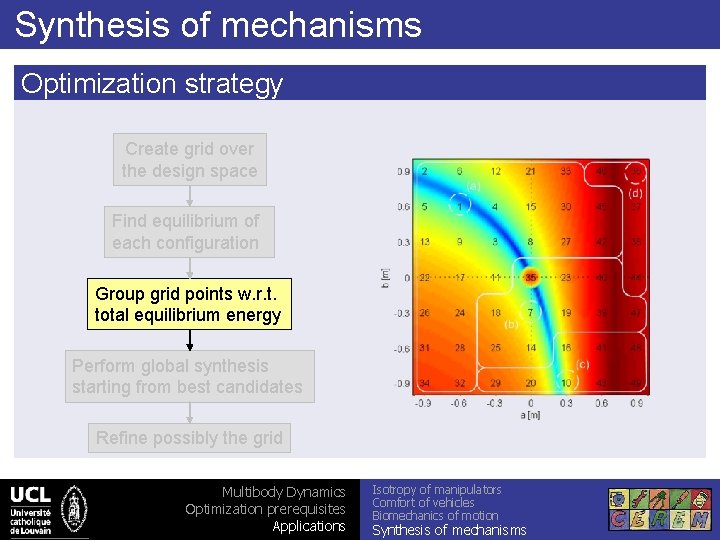
Synthesis of mechanisms Optimization strategy Create grid over the design space Find equilibrium of each configuration Group grid points w. r. t. total equilibrium energy Perform global synthesis starting from best candidates Refine possibly the grid Multibody Dynamics Optimization prerequisites Applications Isotropy of manipulators Comfort of vehicles Biomechanics of motion Synthesis of mechanisms

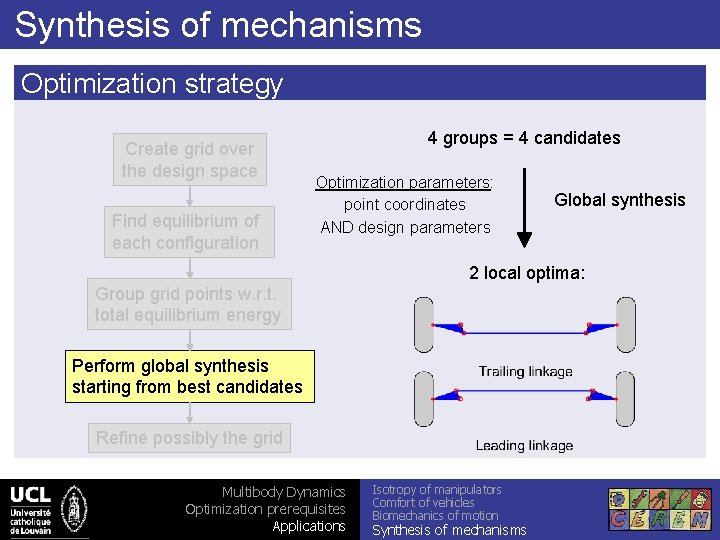
Synthesis of mechanisms Optimization strategy Create grid over the design space Find equilibrium of each configuration 4 groups = 4 candidates Optimization parameters: point coordinates AND design parameters Global synthesis 2 local optima: Group grid points w. r. t. total equilibrium energy Perform global synthesis starting from best candidates Refine possibly the grid Multibody Dynamics Optimization prerequisites Applications Isotropy of manipulators Comfort of vehicles Biomechanics of motion Synthesis of mechanisms

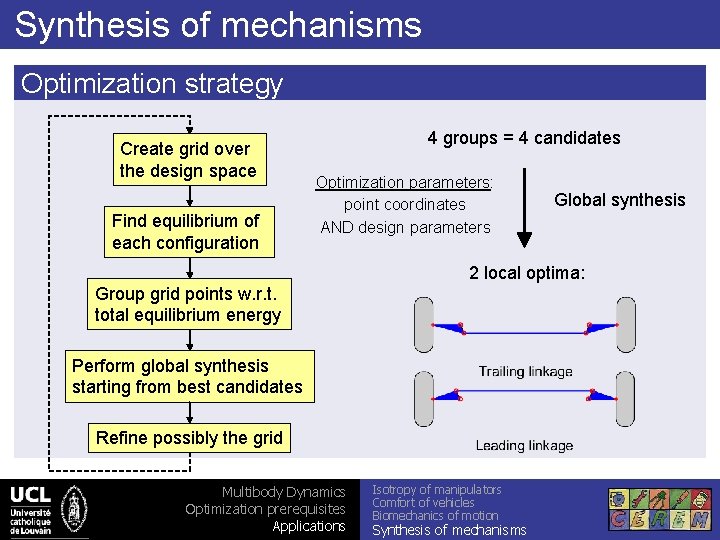
Synthesis of mechanisms Optimization strategy Create grid over the design space Find equilibrium of each configuration 4 groups = 4 candidates Optimization parameters: point coordinates AND design parameters Global synthesis 2 local optima: Group grid points w. r. t. total equilibrium energy Perform global synthesis starting from best candidates Refine possibly the grid Multibody Dynamics Optimization prerequisites Applications Isotropy of manipulators Comfort of vehicles Biomechanics of motion Synthesis of mechanisms

Synthesis of mechanisms Application to six-bar linkage: multiple local optima 83521 grid points 284 groups 14 local optima Additional design criteria 1 « global » optimum Multibody Dynamics Optimization prerequisites Applications Isotropy of manipulators Comfort of vehicles Biomechanics of motion Synthesis of mechanisms

Thank you for your attention