Optimization Linear Programming Duality M Pawan Kumar Slides











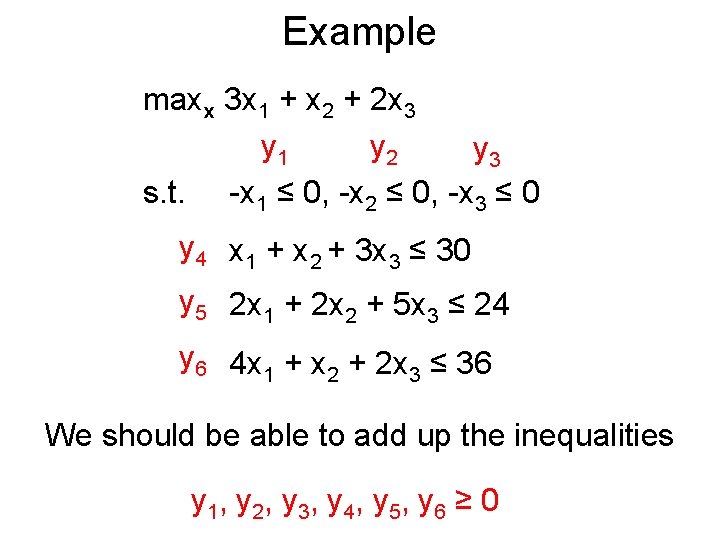

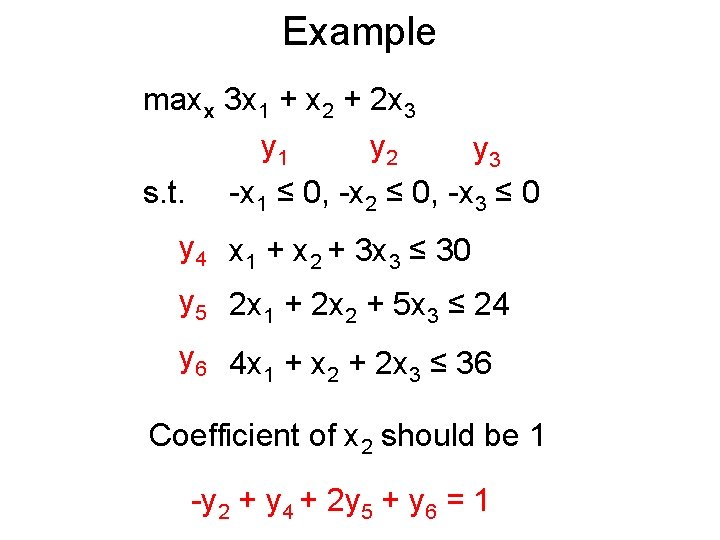




- Slides: 28

Optimization Linear Programming Duality M. Pawan Kumar Slides available online http: //mpawankumar. info

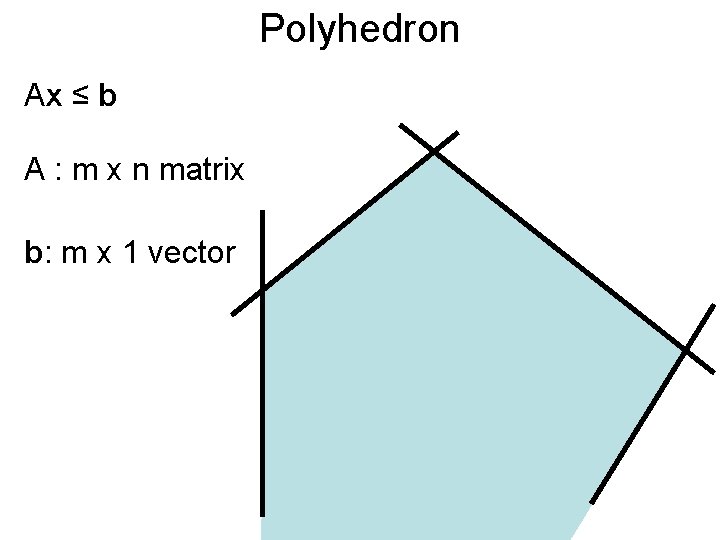
Polyhedron Ax ≤ b A : m x n matrix b: m x 1 vector

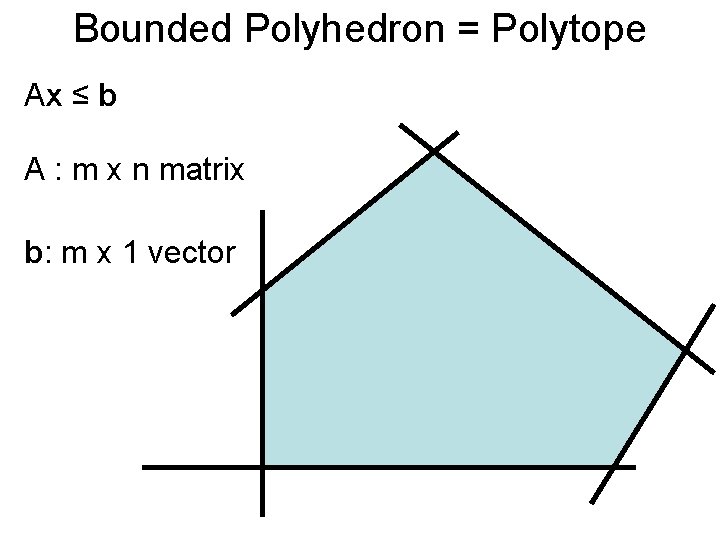
Bounded Polyhedron = Polytope Ax ≤ b A : m x n matrix b: m x 1 vector

Vertex z is a vertex of P = {x, Ax ≤ b} z is not a convex combination of two points in P There does not exist x, y ∈ P and 0 < λ < 1 x ≠ z and y ≠ z such that z = λ x + (1 -λ) y

Vertex z is a vertex of P = {x, Ax ≤ b} Recall A is an m x n matrix Az is a submatrix of A Contains all rows of A such that ai. Tz = bi

Vertex � z is a vertex of P Rank of Az = n Proof?

Outline • Linear Programming • Duality

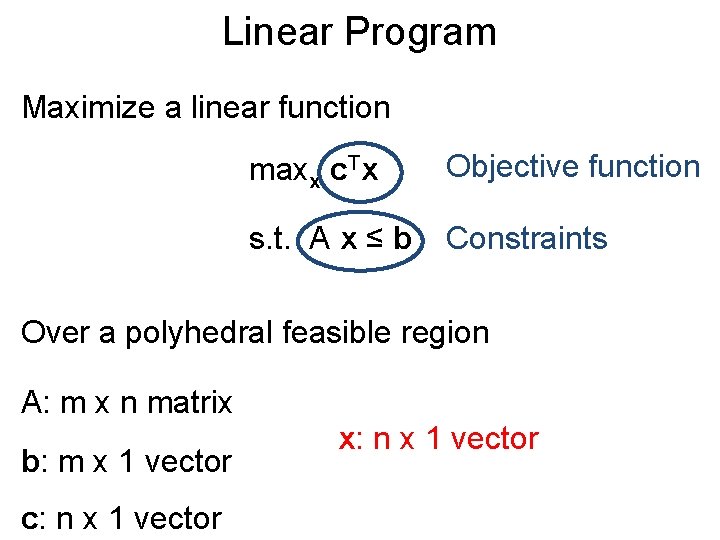
Linear Program Maximize a linear function maxx c. Tx Objective function s. t. A x ≤ b Constraints Over a polyhedral feasible region A: m x n matrix b: m x 1 vector c: n x 1 vector x: n x 1 vector

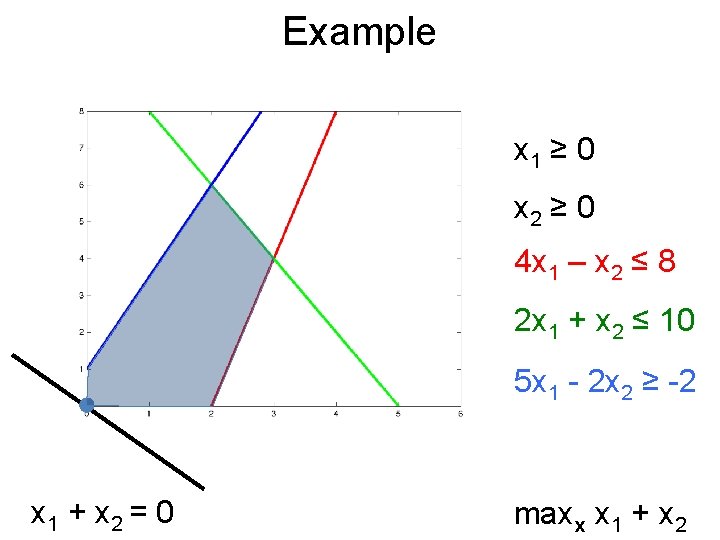
Example maxx x 1 + x 2 s. t. x 1 ≥ 0 x 2 ≥ 0 4 x 1 – x 2 ≤ 8 2 x 1 + x 2 ≤ 10 5 x 1 - 2 x 2 ≥ -2 What is c? A? b?

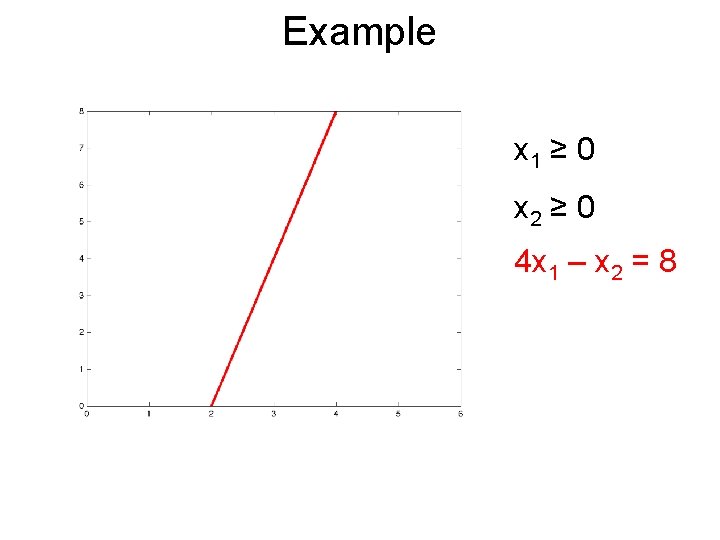
Example x 1 ≥ 0 x 2 ≥ 0

Example x 1 ≥ 0 x 2 ≥ 0 4 x 1 – x 2 = 8

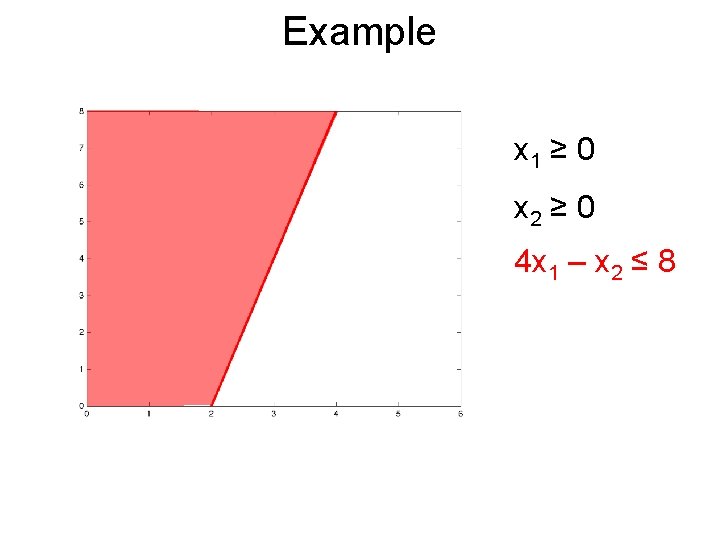
Example x 1 ≥ 0 x 2 ≥ 0 4 x 1 – x 2 ≤ 8

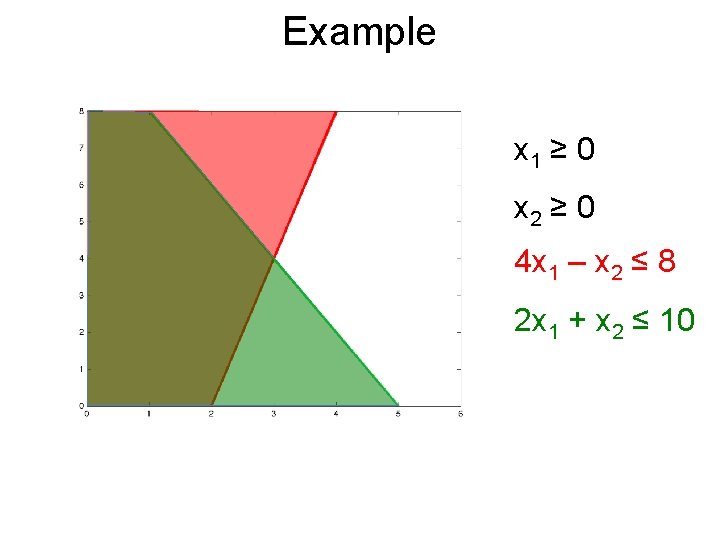
Example x 1 ≥ 0 x 2 ≥ 0 4 x 1 – x 2 ≤ 8 2 x 1 + x 2 ≤ 10

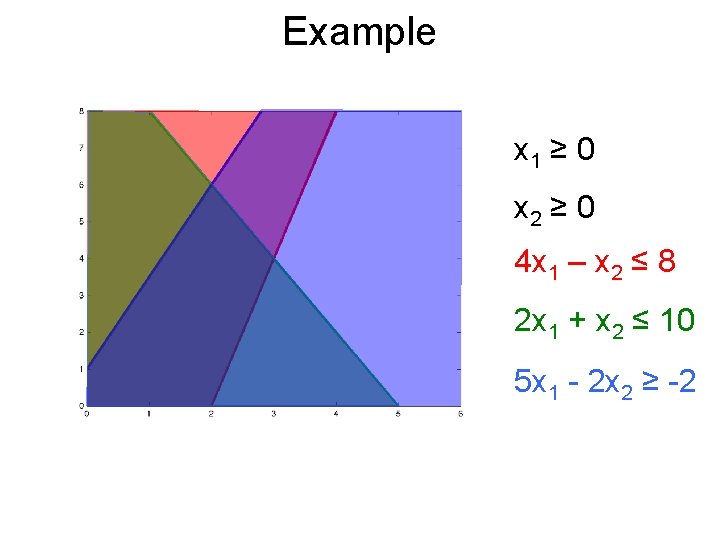
Example x 1 ≥ 0 x 2 ≥ 0 4 x 1 – x 2 ≤ 8 2 x 1 + x 2 ≤ 10 5 x 1 - 2 x 2 ≥ -2

Example x 1 ≥ 0 x 2 ≥ 0 4 x 1 – x 2 ≤ 8 2 x 1 + x 2 ≤ 10 5 x 1 - 2 x 2 ≥ -2 x 1 + x 2 = 0 maxx x 1 + x 2

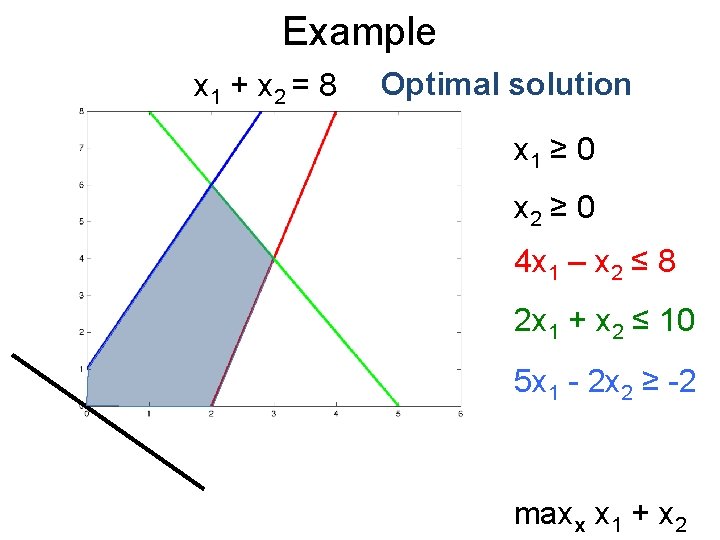
Example x 1 + x 2 = 8 Optimal solution x 1 ≥ 0 x 2 ≥ 0 4 x 1 – x 2 ≤ 8 2 x 1 + x 2 ≤ 10 5 x 1 - 2 x 2 ≥ -2 maxx x 1 + x 2

Optimal Solutions An LP can have more than one optimal solution Example? At least one optimal solution is a vertex Proof?

Outline • Linear Programming • Duality

Example maxx 3 x 1 + x 2 + 2 x 3 7 x 2 x s. t. -x 1 ≤ 0, -x 2 ≤ 0, -x 3 ≤ 0 3 x x 1 + x 2 + 3 x 3 ≤ 30 2 x 1 + 2 x 2 + 5 x 3 ≤ 24 4 x 1 + x 2 + 2 x 3 ≤ 36 Scale the constraints, add them up 3 x 1 + x 2 + 2 x 3 ≤ 90 Upper bound on solution

Example maxx 3 x 1 + x 2 + 2 x 3 1 x s. t. -x 1 ≤ 0, -x 2 ≤ 0, -x 3 ≤ 0 x 1 + x 2 + 3 x 3 ≤ 30 2 x 1 + 2 x 2 + 5 x 3 ≤ 24 1 x 4 x 1 + x 2 + 2 x 3 ≤ 36 Scale the constraints, add them up 3 x 1 + x 2 + 2 x 3 ≤ 36 Upper bound on solution

Example maxx 3 x 1 + x 2 + 2 x 3 1 x s. t. -x 1 ≤ 0, -x 2 ≤ 0, -x 3 ≤ 0 x 1 + x 2 + 3 x 3 ≤ 30 2 x 1 + 2 x 2 + 5 x 3 ≤ 24 1 x 4 x 1 + x 2 + 2 x 3 ≤ 36 Scale the constraints, add them up 3 x 1 + x 2 + 2 x 3 ≤ 36 Tightest upper bound?
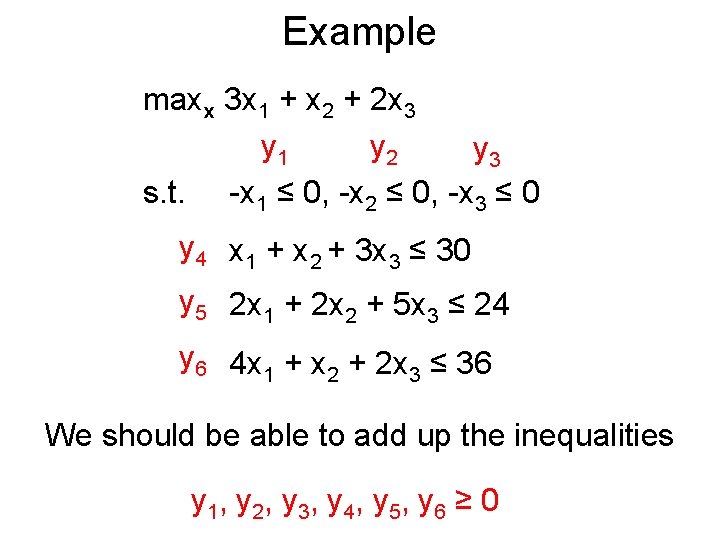
Example maxx 3 x 1 + x 2 + 2 x 3 y 1 y 2 y 3 s. t. -x 1 ≤ 0, -x 2 ≤ 0, -x 3 ≤ 0 y 4 x 1 + x 2 + 3 x 3 ≤ 30 y 5 2 x 1 + 2 x 2 + 5 x 3 ≤ 24 y 6 4 x 1 + x 2 + 2 x 3 ≤ 36 We should be able to add up the inequalities y 1, y 2, y 3, y 4, y 5, y 6 ≥ 0

Example maxx 3 x 1 + x 2 + 2 x 3 y 1 y 2 y 3 s. t. -x 1 ≤ 0, -x 2 ≤ 0, -x 3 ≤ 0 y 4 x 1 + x 2 + 3 x 3 ≤ 30 y 5 2 x 1 + 2 x 2 + 5 x 3 ≤ 24 y 6 4 x 1 + x 2 + 2 x 3 ≤ 36 Coefficient of x 1 should be 3 -y 1 + y 4 + 2 y 5 + 4 y 6 = 3
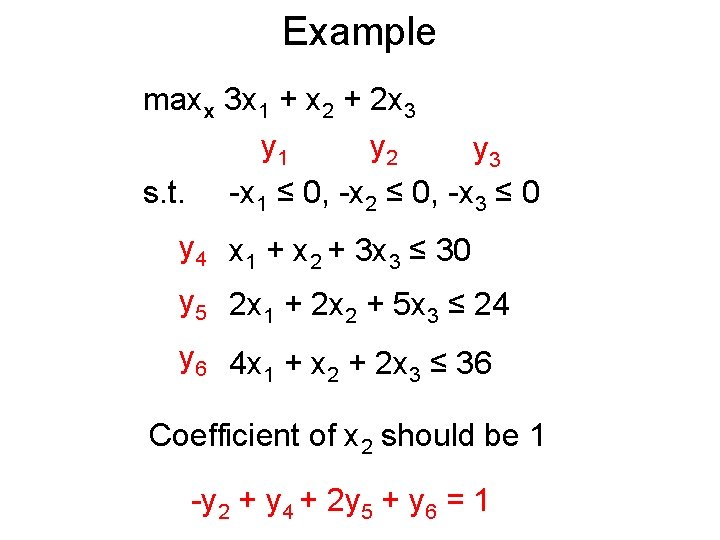
Example maxx 3 x 1 + x 2 + 2 x 3 y 1 y 2 y 3 s. t. -x 1 ≤ 0, -x 2 ≤ 0, -x 3 ≤ 0 y 4 x 1 + x 2 + 3 x 3 ≤ 30 y 5 2 x 1 + 2 x 2 + 5 x 3 ≤ 24 y 6 4 x 1 + x 2 + 2 x 3 ≤ 36 Coefficient of x 2 should be 1 -y 2 + y 4 + 2 y 5 + y 6 = 1

Example maxx 3 x 1 + x 2 + 2 x 3 y 1 y 2 y 3 s. t. -x 1 ≤ 0, -x 2 ≤ 0, -x 3 ≤ 0 y 4 x 1 + x 2 + 3 x 3 ≤ 30 y 5 2 x 1 + 2 x 2 + 5 x 3 ≤ 24 y 6 4 x 1 + x 2 + 2 x 3 ≤ 36 Coefficient of x 3 should be 2 -y 3 + 3 y 4 + 5 y 5 + 2 y 6 = 2

Example maxx 3 x 1 + x 2 + 2 x 3 y 1 y 2 y 3 s. t. -x 1 ≤ 0, -x 2 ≤ 0, -x 3 ≤ 0 y 4 x 1 + x 2 + 3 x 3 ≤ 30 y 5 2 x 1 + 2 x 2 + 5 x 3 ≤ 24 y 6 4 x 1 + x 2 + 2 x 3 ≤ 36 Upper bound should be tightest miny 30 y 4 + 24 y 5 + 36 y 6

Dual miny 30 y 4 + 24 y 5 + 36 y 6 s. t. y 1, y 2, y 3, y 4, y 5, y 6 ≥ 0 -y 1 + y 4 + 2 y 5 + 4 y 6 = 3 -y 2 + y 4 + 2 y 5 + y 6 = 1 -y 3 + 3 y 4 + 5 y 5 + 2 y 6 = 2 Original problem is called primal Dual of dual is primal

Questions?