Optimization for Operation of Power Systems with Performance

Optimization for Operation of Power Systems with Performance Guarantee by Gokturk Poyrazoglu University at Buffalo, SUNY Department of Electrical Engineering

Electricity Supply Chain G n o i t a ener Tra on i s s i nsm D n o i t u istrib C r e m onsu

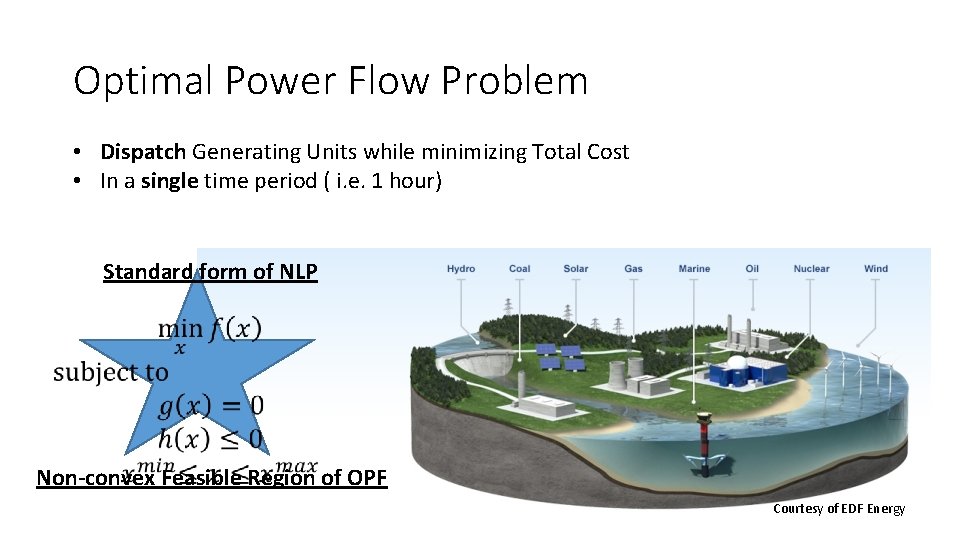
Optimal Power Flow Problem • Dispatch Generating Units while minimizing Total Cost • In a single time period ( i. e. 1 hour) Standard form of NLP Non-convex Feasible Region of OPF Courtesy of EDF Energy

Unit Commitment • Select and Dispatch Generating Units while minimizing Total Cost • In a multi time period ( i. e. 1 day or 1 week) t=1 t=2 t=3 t=4 Time t=5

Unit Commitment with DC Model • Select and Dispatch Generating Units while minimizing Total Cost • In a multi time period ( i. e. 1 day or 1 week) t=1 t=2 t=3 t=4 Time t=5

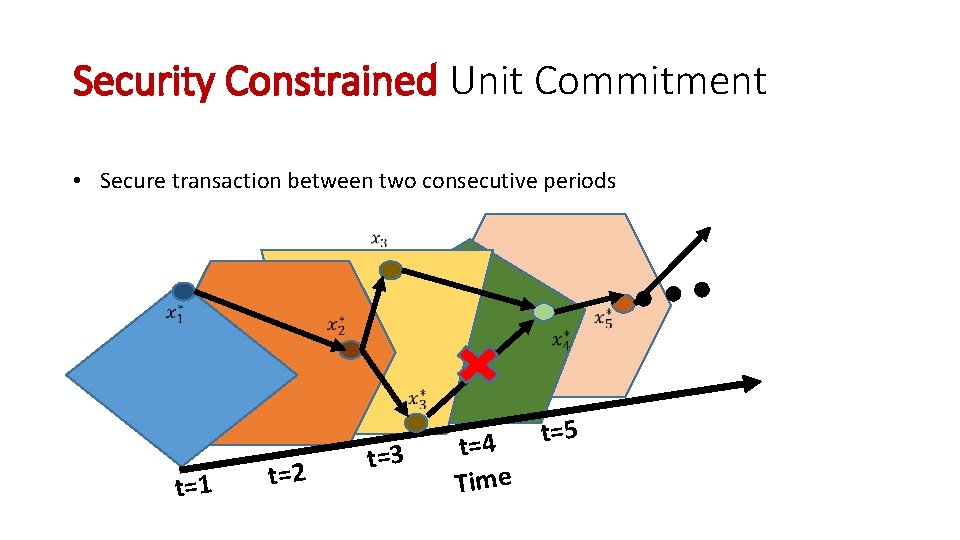
Security Constrained Unit Commitment • Secure transaction between two consecutive periods t=1 t=2 t=3 t=4 Time t=5

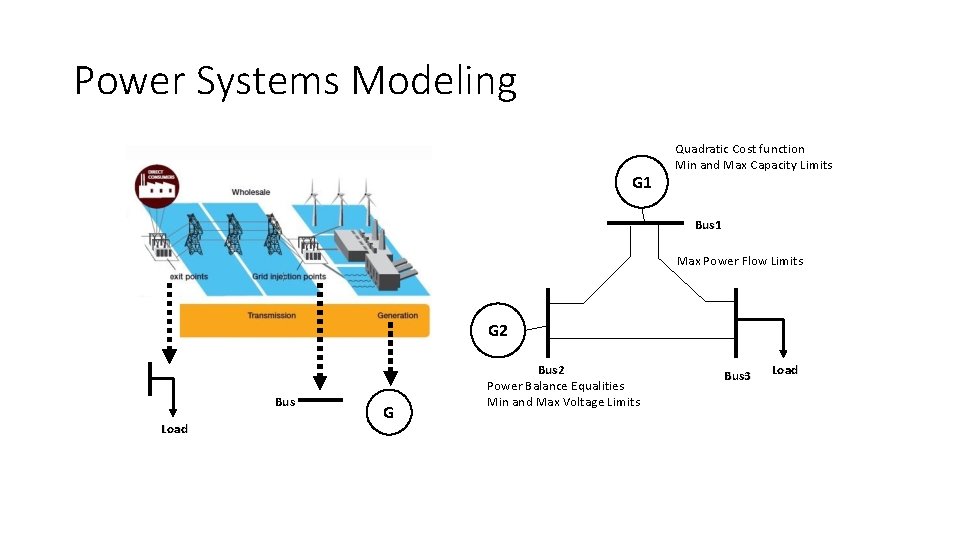
Power Systems Modeling G 1 Quadratic Cost function Min and Max Capacity Limits Bus 1 Max Power Flow Limits G 2 Bus Load G Bus 2 Power Balance Equalities Min and Max Voltage Limits Bus 3 Load

Transmission Switching Simulation VS Reality G 1 Bus 1 G 2 Bus 3 Load

PART I Optimal Topology Control with Physical Power Flow Constraints and N-1 Contingency Criterion This study was partially published in the following journal and conferences. University at Buffalo, SUNY Department of Electrical Engineering

Problem Definition Ø AC Optimal Power Flow: Nonlinear and nonconvex programming (NLP or QCQP) Ø AC OPF with optimal topology control: Mixed integer nonlinear and nonconvex programming (MINLP) Ø Same N-1 reliability consideration as the original topology • Line contingencies • Large-scale problem

Challenges Ø Comparison of OPF solutions among multiple topologies Ø NLP solvers seek for a local optimum Ø Guarantee a better topology? • NLP solutions may not reflect the quality of the global solution • Therefore, comparison between two NLP solutions does not guarantee optimal topology

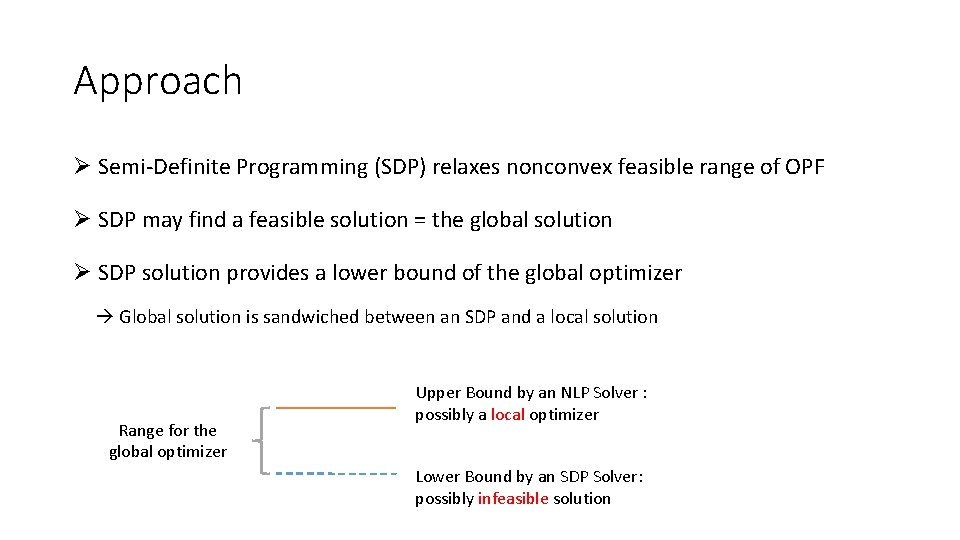
Approach Ø Semi-Definite Programming (SDP) relaxes nonconvex feasible range of OPF Ø SDP may find a feasible solution = the global solution Ø SDP solution provides a lower bound of the global optimizer Global solution is sandwiched between an SDP and a local solution Range for the global optimizer Upper Bound by an NLP Solver : possibly a local optimizer Lower Bound by an SDP Solver: possibly infeasible solution

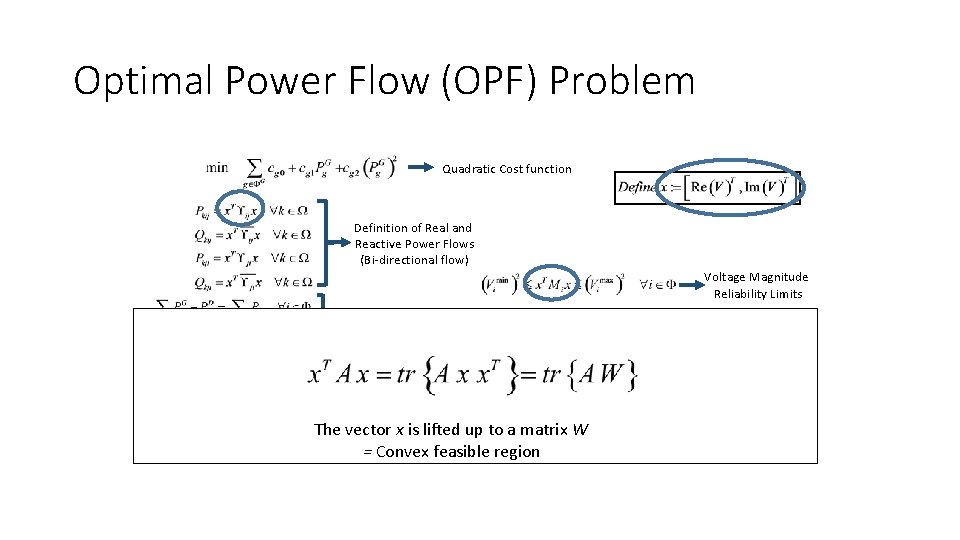
Optimal Power Flow (OPF) Problem Quadratic Cost function Definition of Real and Reactive Power Flows (Bi-directional flow) Voltage Magnitude Reliability Limits Real and Reactive Power Balance Real and Reactive Generation Capacity Limits Maximum Power Flow Limits (bi-directional flow) The vector x is lifted up to a matrix W OPF problem is given in the form of Non-convex Quadratically Constrained Quadratic Programming (QCQP) = Convex feasible region

SDP Relaxation Real and Reactive & Power Balance Real and Reactive Generation Capacity Limits Voltage Magnitude Reliability Limits Maximum Power Flow Limits(bi-directional flow) Schur Compliment of Quadratic Cost function Positive Semi-definite Matrix & Reference Angle

SDP Relaxation Topology Χ and Υ (original topology) Ø Utilize the sandwich structure of the global solution • NLP solution of Χ < SDP solution of Υ ≤ Global solution of Υ • A local optimizer of Χ is better than the global optimizer of Υ Topology Χ Topology Υ Ø Aim to find such a topology Χ in this study

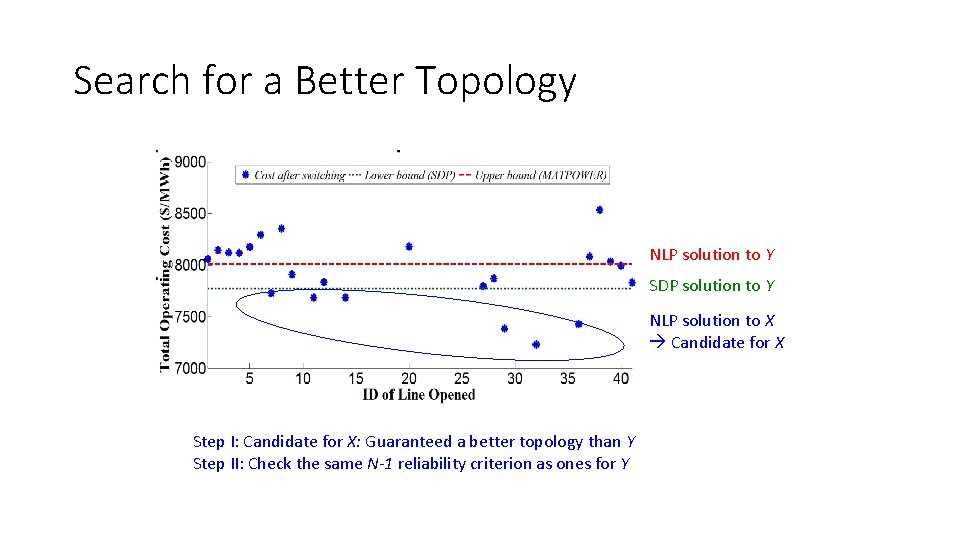
Search for a Better Topology NLP solution to Υ SDP solution to Υ NLP solution to Χ Candidate for Χ Step I: Candidate for Χ: Guaranteed a better topology than Υ Step II: Check the same N-1 reliability criterion as ones for Υ

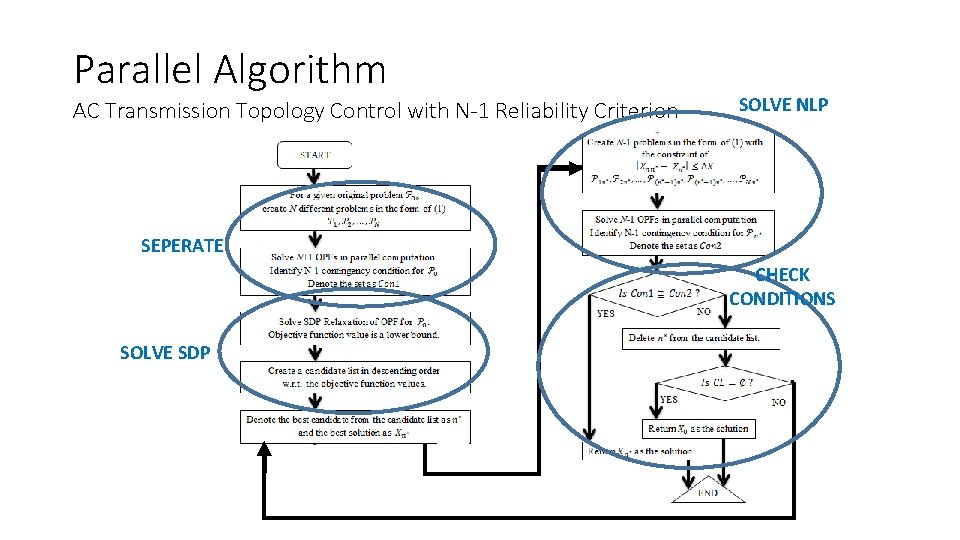
Parallel Algorithm AC Transmission Topology Control with N-1 Reliability Criterion SOLVE NLP SEPERATE CHECK CONDITIONS SOLVE SDP

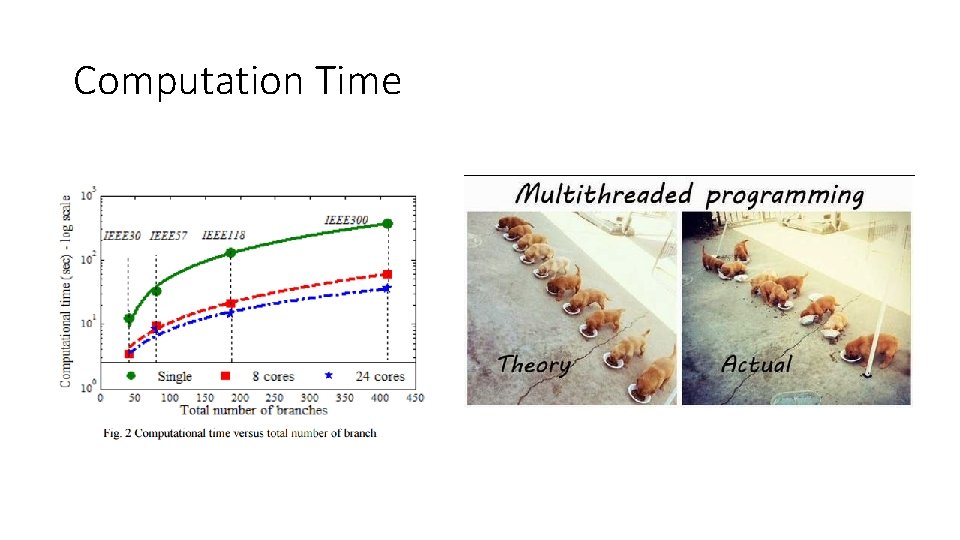
Computation Time

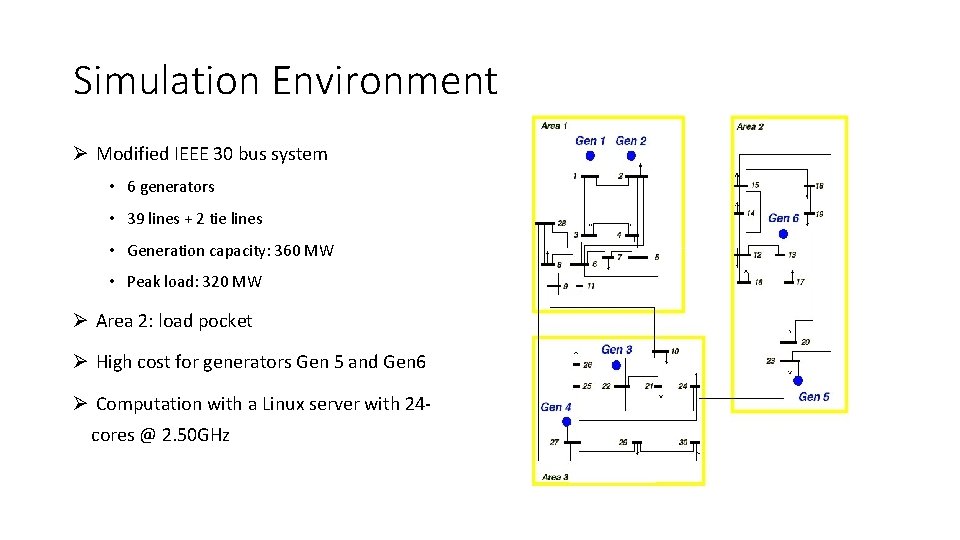
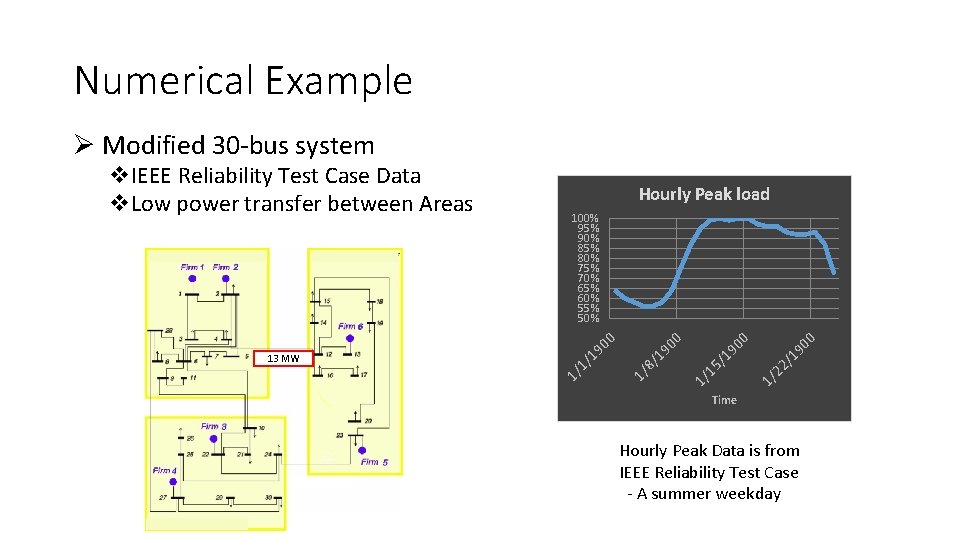
Simulation Environment Ø Modified IEEE 30 bus system • 6 generators • 39 lines + 2 tie lines • Generation capacity: 360 MW • Peak load: 320 MW Ø Area 2: load pocket Ø High cost for generators Gen 5 and Gen 6 Ø Computation with a Linux server with 24 cores @ 2. 50 GHz

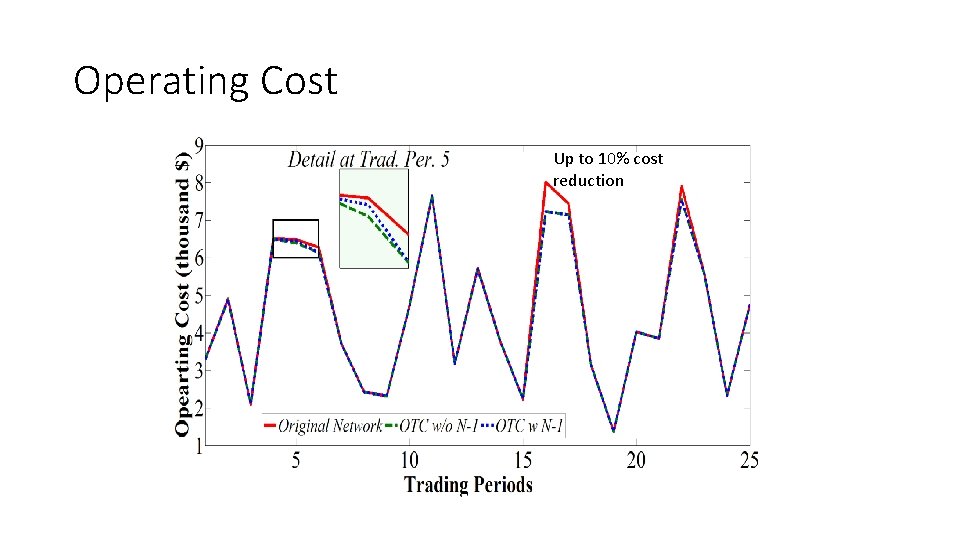
Operating Cost Up to 10% cost reduction

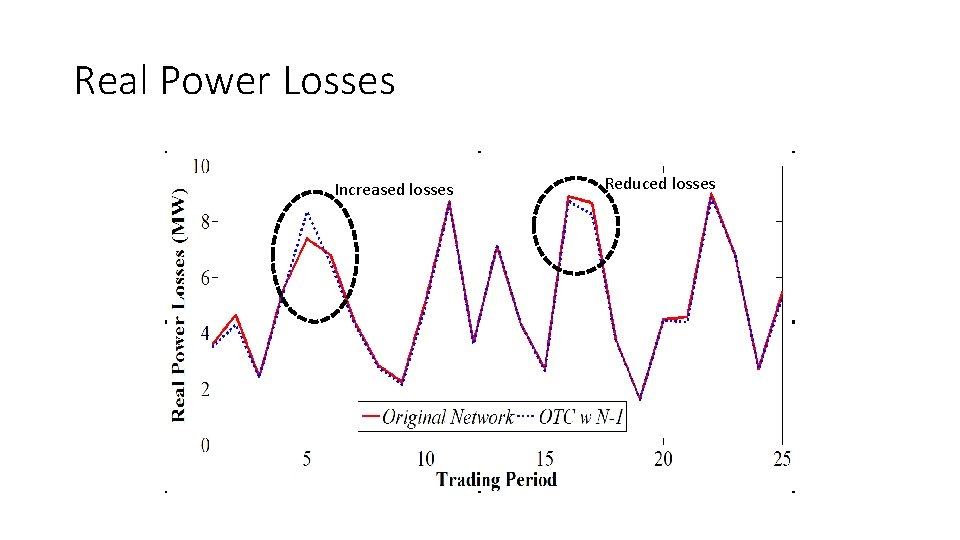
Real Power Losses Increased losses Reduced losses

Conclusion Ø Efficient algorithm to implement topology control in the restructured electricity market experiments Ø Identified topology • Guaranteed a better one • Satisfy the same reliability criterion Ø Topology control finds a solution with • Decreased system cost but • Losses may increase

PART II Scheduling Maintenance for Reliable Transmission System (The SMa. RTS Model) This study will be partially published in the following journal and conferences. University at Buffalo, SUNY Department of Electrical Engineering

What is the SMa. RTS Model? Scheduling Maintenance for Reliable Transmission System ØCombination of studies on power economics v. Security Constrained Unit Commitment v. Transmission Topology Control TTC N-1 SMa. RTS v. Outage Coordination v. N-1 Reliability Criterion SCUC

Security Constrained Unit Commitment (SCUC) Ø Selection of generator units Ø Minimize total operating cost Ø Security on ramp up and ramp down of units Ø Mixed Integer Linear Programming (MILP) ØBeing used widely in business

Transmission Topology Control (TTC) Ø Selection of branches to keep in service Ø Minimize total operating cost Ø Security on ramp up and ramp down of units Ø Mixed Integer Linear Programming (MILP) Ø No reported use in business

Challenges of Topology Control Ø Transient Stability Concerns v Switching effect Ø Cost of Switching v Who will pay? Ø Financial Transmission Rights (FTR) Market v Unwillingness of market participants

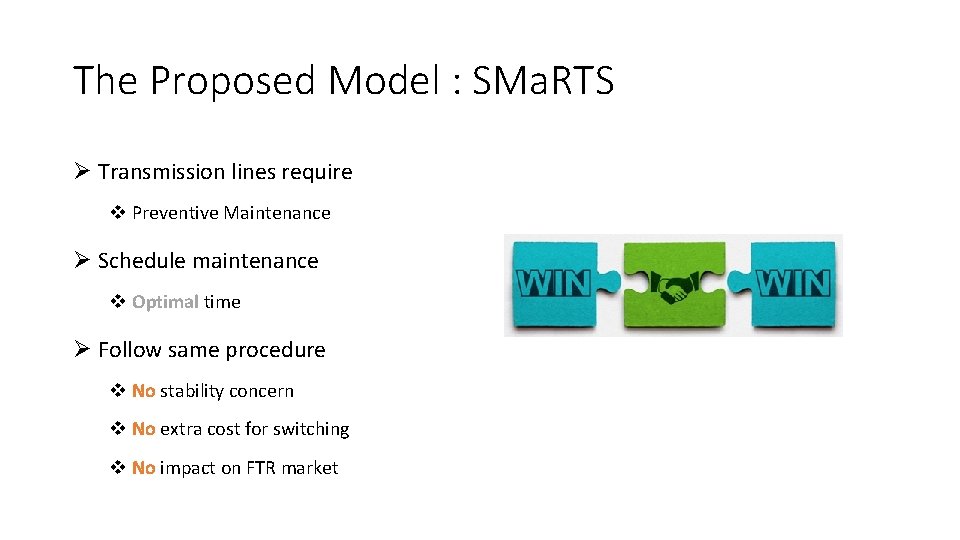
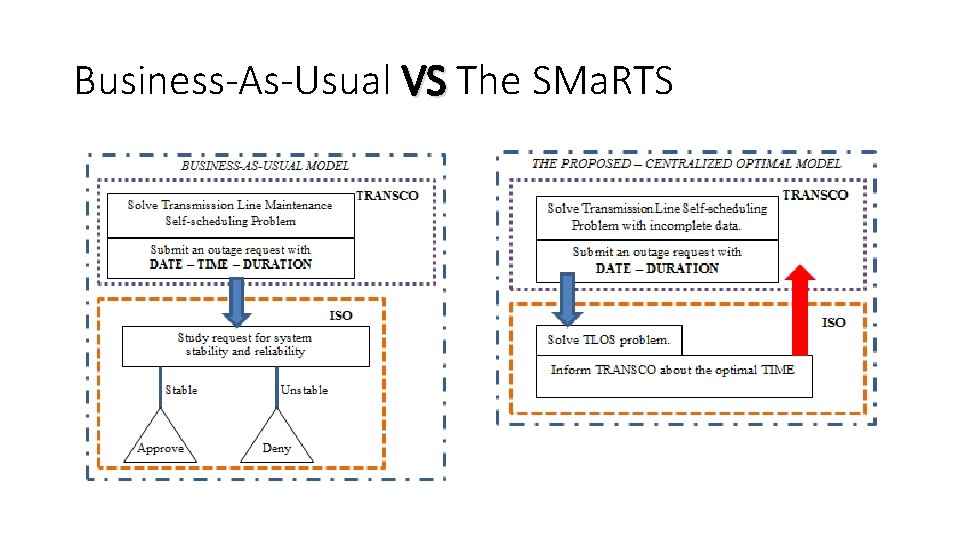
The Proposed Model : SMa. RTS Ø Transmission lines require v Preventive Maintenance Ø Schedule maintenance v Optimal time Ø Follow same procedure v No stability concern v No extra cost for switching v No impact on FTR market

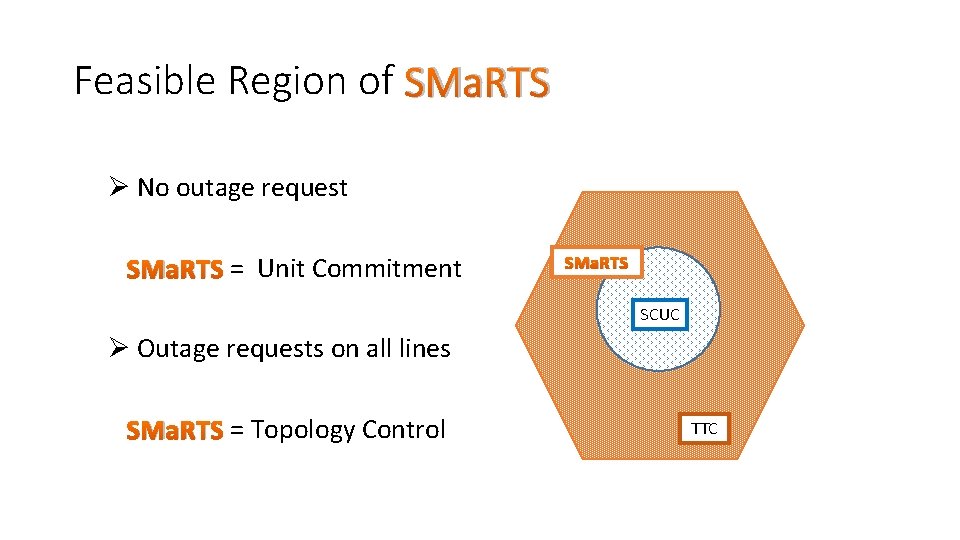
Feasible Region of SMa. RTS Ø No outage request SMa. RTS = Unit Commitment SMa. RTS SCUC Ø Outage requests on all lines SMa. RTS = Topology Control TTC

Business-As-Usual VS The SMa. RTS

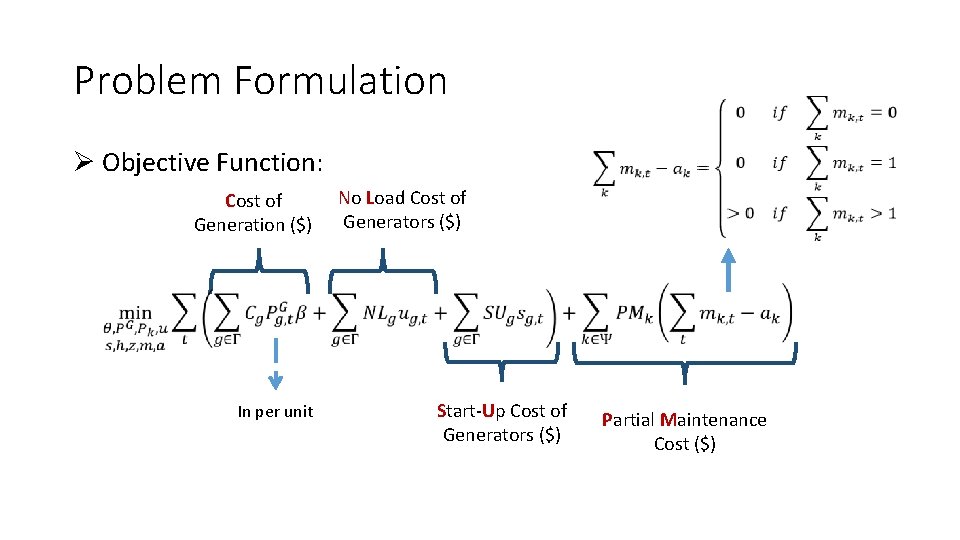
Problem Formulation Ø Objective Function: Cost of Generation ($) No Load Cost of Generators ($) In per unit Start-Up Cost of Generators ($) Partial Maintenance Cost ($)

Power Balance Constraints & Power Flow Definitions • Power flow definitions - Maintenance requested Lines - Other lines • Reference Voltage Angle • Real Power Balance Equalities

Box Constraints • Generation be in between capacity limits • Max. Power flow limits are enforced • The change in generation should be applicable.

Maintenance Scheduling Constraints • Definition of maintenance start variable • Definition of approval status & Limitation on partial maintenance (optional) • Limit on maintenance duration • Complete maintenance in planning horizon

Unit Commitment Constraints • Definition of unit commitment variables • Limit on minimum up-time • Limit on minimum down-time

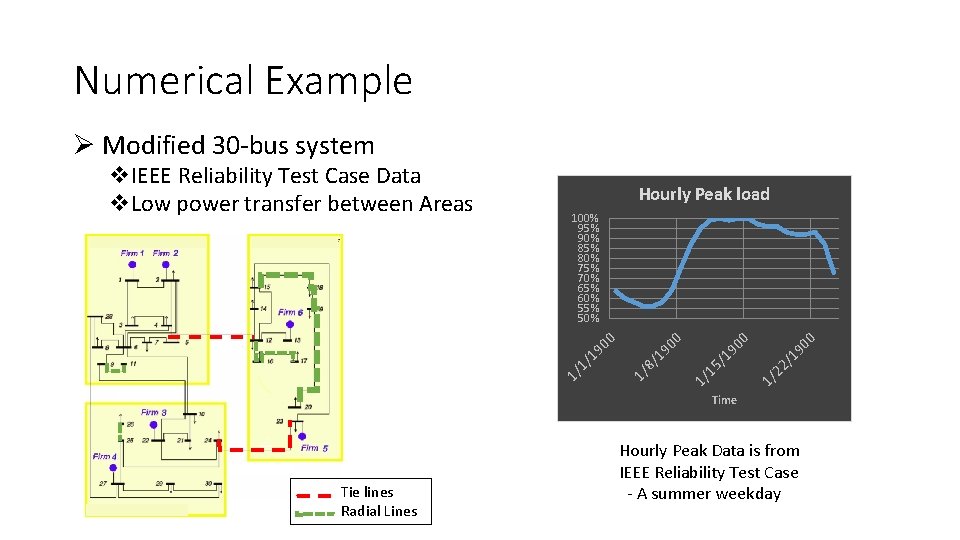
Numerical Example Ø Modified 30 -bus system Hourly Peak load 0 22 /1 90 1/ 0 15 /1 90 1/ 8/ 1/ 19 0 1/ 1/ 13 MW 19 00 100% 95% 90% 85% 80% 75% 70% 65% 60% 55% 50% 0 v. IEEE Reliability Test Case Data v. Low power transfer between Areas Time Hourly Peak Data is from IEEE Reliability Test Case - A summer weekday

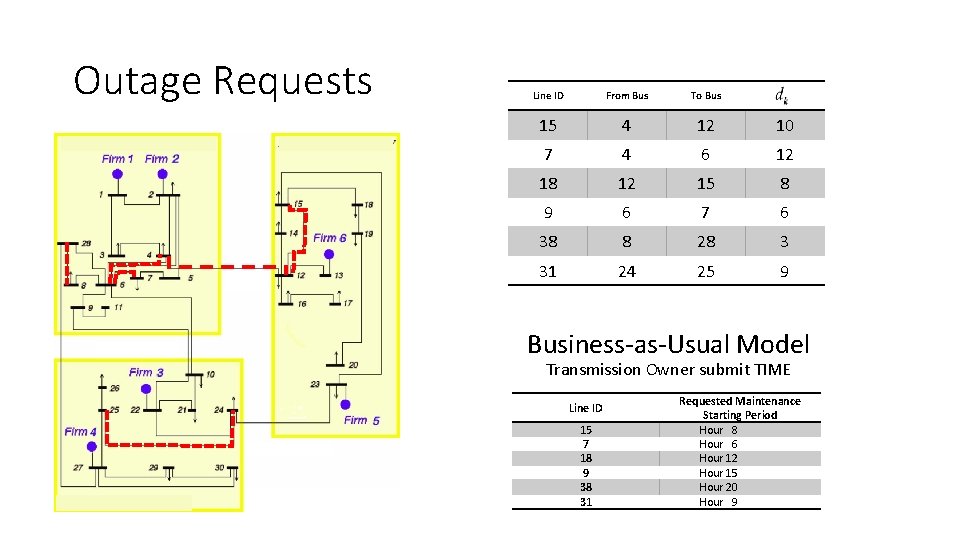
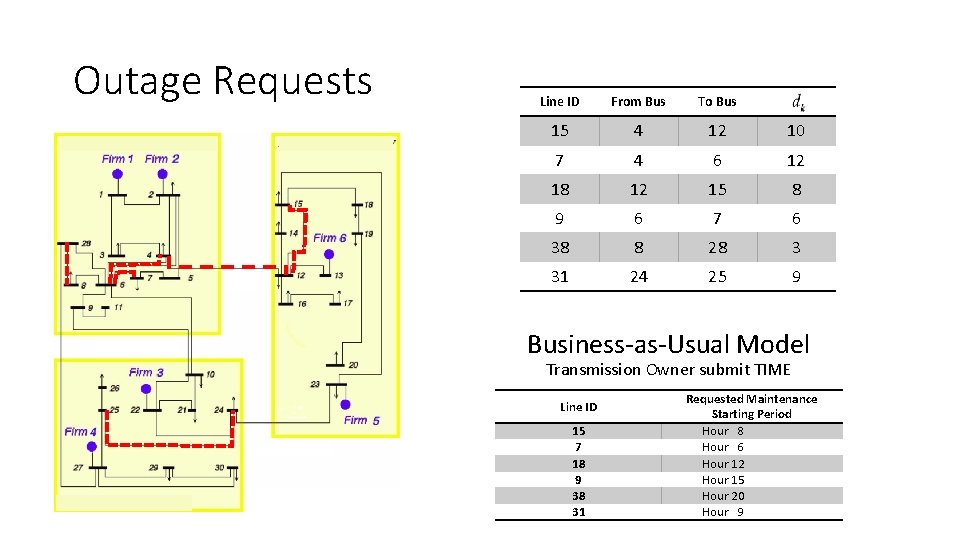
Outage Requests Line ID From Bus To Bus 15 4 12 10 7 4 6 12 18 12 15 8 9 6 7 6 38 8 28 3 31 24 25 9 Business-as-Usual Model Transmission Owner submit TIME Line ID 15 7 18 9 38 31 Requested Maintenance Starting Period Hour 8 Hour 6 Hour 12 Hour 15 Hour 20 Hour 9

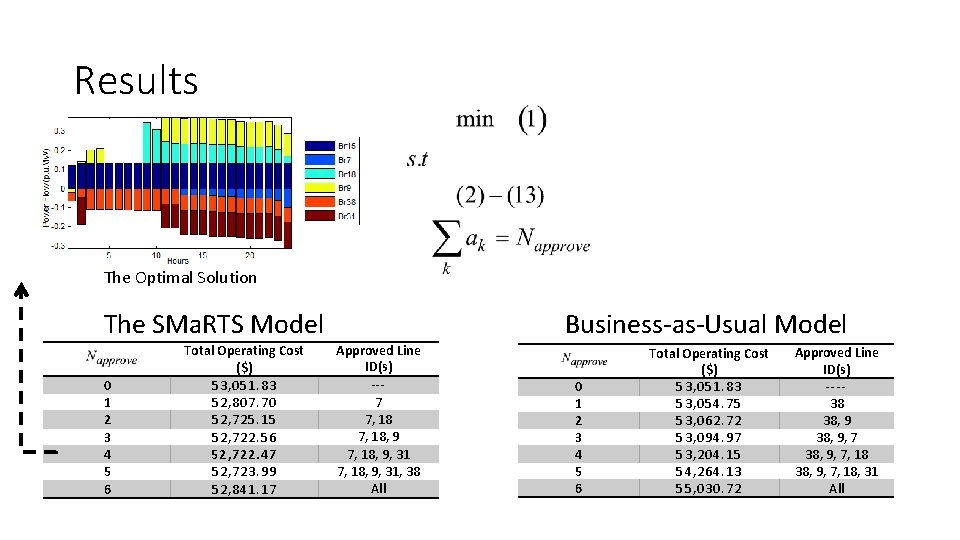
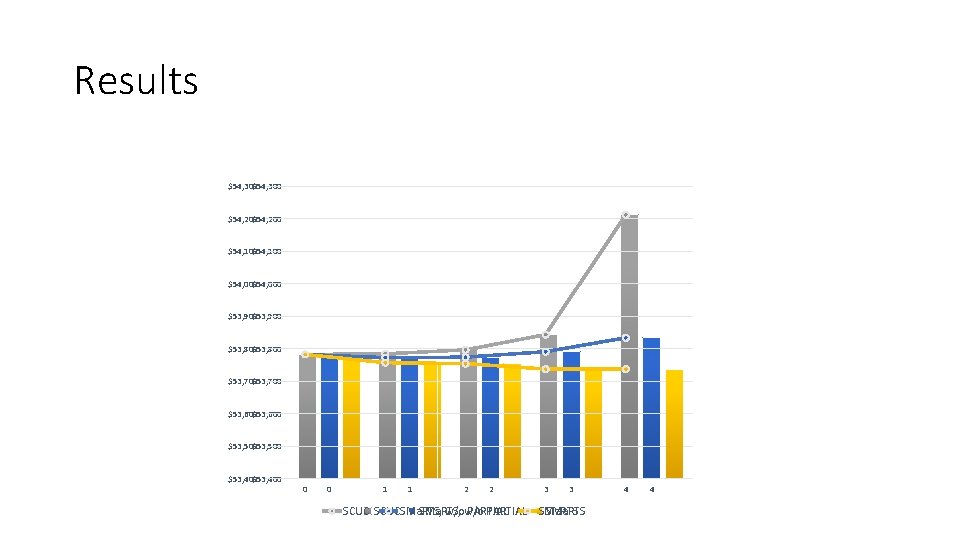
Results The Optimal Solution The SMa. RTS Model 0 1 2 3 4 5 6 Total Operating Cost ($) 53, 051. 83 52, 807. 70 52, 725. 15 52, 722. 56 52, 722. 47 52, 723. 99 52, 841. 17 Business-as-Usual Model Approved Line ID(s) --7 7, 18, 9, 31, 38 All 0 1 2 3 4 5 6 Total Operating Cost ($) 53, 051. 83 53, 054. 75 53, 062. 72 53, 094. 97 53, 204. 15 54, 264. 13 55, 030. 72 Approved Line ID(s) ---38 38, 9, 7, 18, 31 All

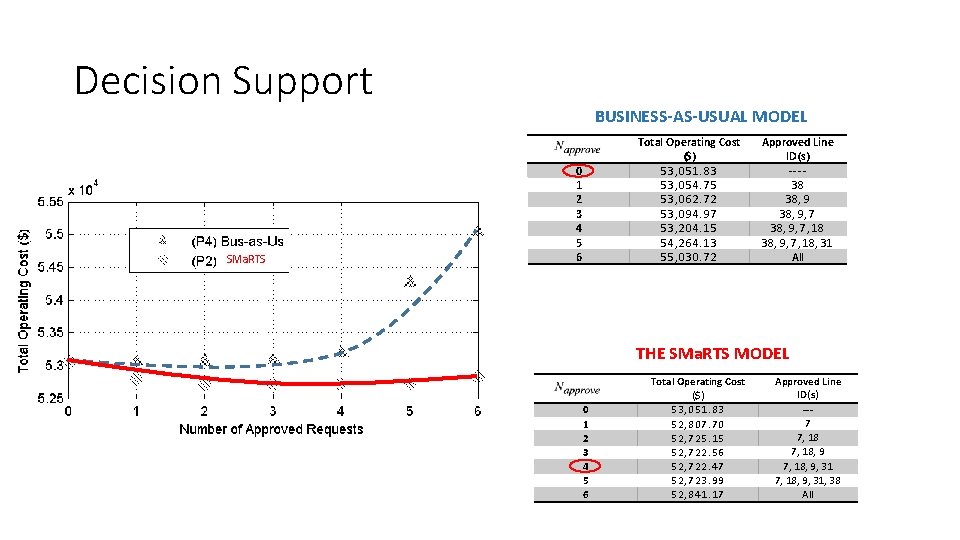
Decision Support SMa. RTS BUSINESS-AS-USUAL MODEL Total Operating Cost ($) 53, 051. 83 53, 054. 75 53, 062. 72 53, 094. 97 53, 204. 15 54, 264. 13 55, 030. 72 0 1 2 3 4 5 6 Approved Line ID(s) ---38 38, 9, 7, 18, 31 All THE SMa. RTS MODEL 0 1 2 3 4 5 6 Total Operating Cost ($) 53, 051. 83 52, 807. 70 52, 725. 15 52, 722. 56 52, 722. 47 52, 723. 99 52, 841. 17 Approved Line ID(s) --7 7, 18, 9, 31, 38 All

The SMa. RTS Model with N-1 Reliability University at Buffalo, SUNY Department of Electrical Engineering

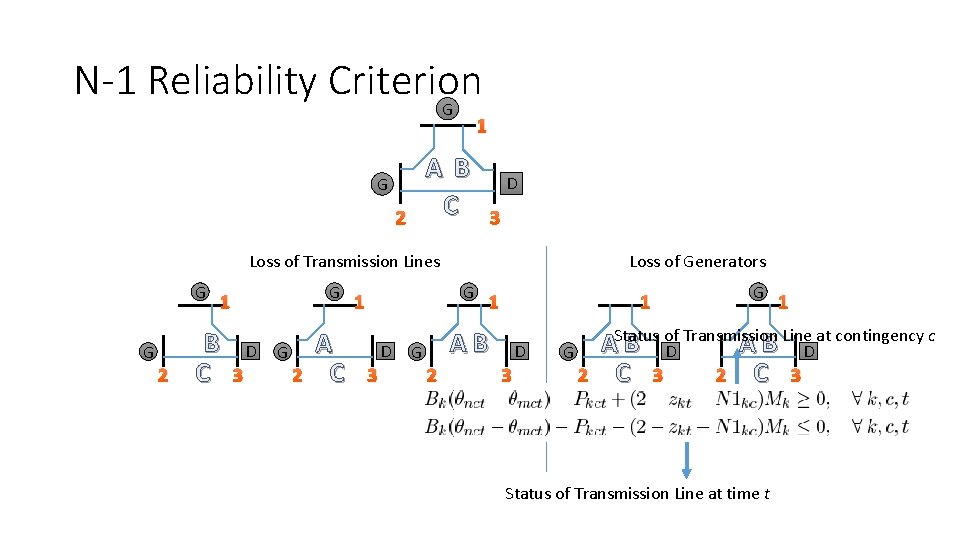
N-1 Reliability Criterion G 1 A B C G 2 D 3 Loss of Transmission Lines G G 2 B C G 1 D 3 G 2 A C Loss of Generators G 1 D 3 1 1 AB G 2 D 3 G 2 G 1 B D AStatus of Transmission Line at contingency c C 3 2 C 3 Status of Transmission Line at time t

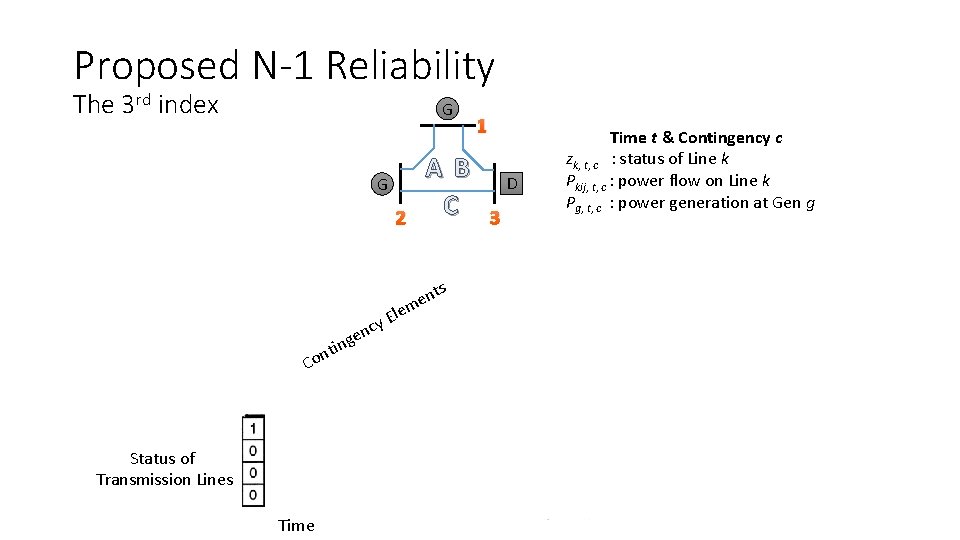
Proposed N-1 Reliability The 3 rd index G A B C G 2 le nt e m E y c n ge n i nt Co Status of Transmission Lines Time s 1 D 3 Time t & Contingency c zk, t, c : status of Line k Pkij, t, c : power flow on Line k Pg, t, c : power generation at Gen g

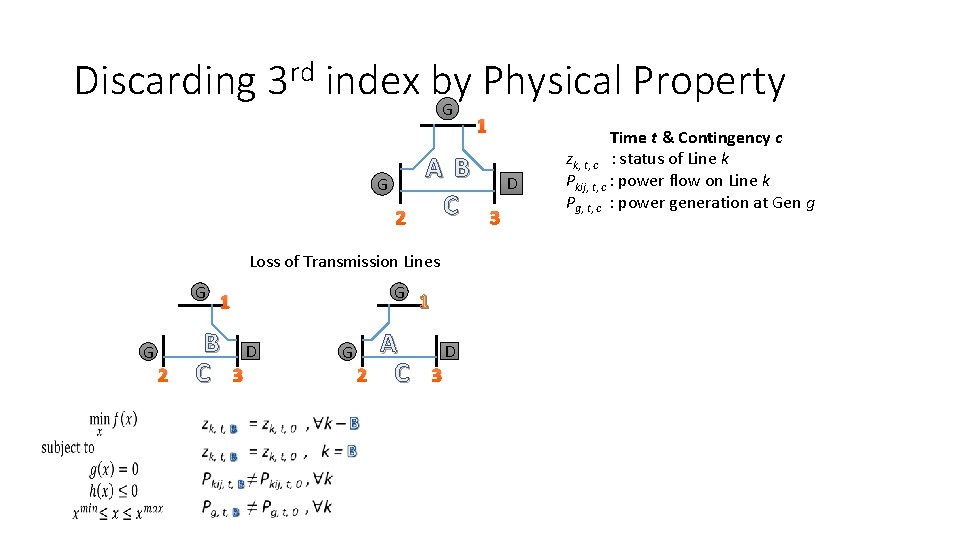
Discarding 3 rd index by Physical Property G 1 G 2 A B C Loss of Transmission Lines G G 2 B C G 1 D 3 G 2 A C 1 D 3 Time t & Contingency c zk, t, c : status of Line k Pkij, t, c : power flow on Line k Pg, t, c : power generation at Gen g

Utilizing Physical Meaning Discard 3 rd index & a variable Transmission Line Contingency Enforce the flow to be ZERO Generation Contingency Enforce the generation to be ZERO

Numerical Example Ø Modified 30 -bus system Hourly Peak load 0 22 /1 90 1/ 0 15 /1 90 1/ 8/ 1/ 19 0 1/ 1/ 19 00 100% 95% 90% 85% 80% 75% 70% 65% 60% 55% 50% 0 v. IEEE Reliability Test Case Data v. Low power transfer between Areas Time Tie lines Radial Lines Hourly Peak Data is from IEEE Reliability Test Case - A summer weekday

Outage Requests Line ID From Bus To Bus 15 4 12 10 7 4 6 12 18 12 15 8 9 6 7 6 38 8 28 3 31 24 25 9 Business-as-Usual Model Transmission Owner submit TIME Line ID 15 7 18 9 38 31 Requested Maintenance Starting Period Hour 8 Hour 6 Hour 12 Hour 15 Hour 20 Hour 9

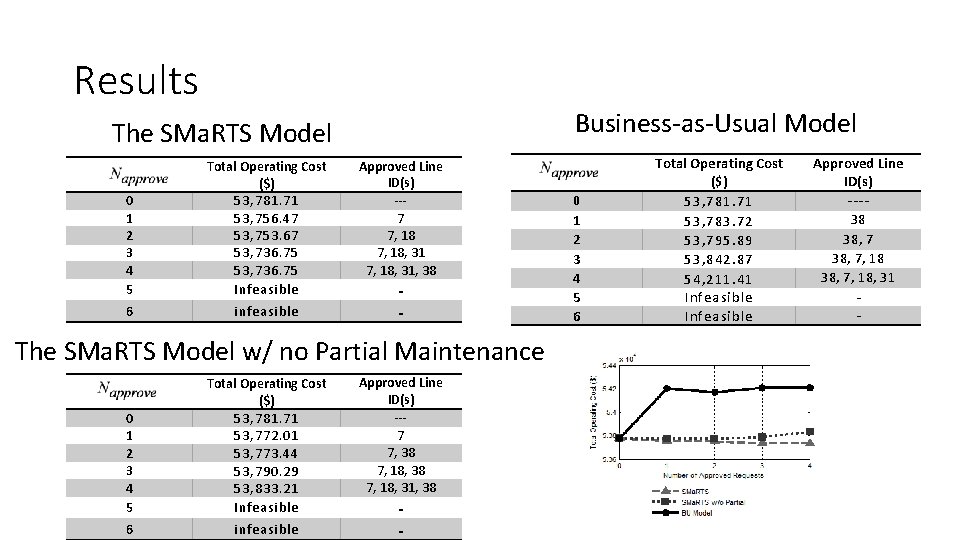
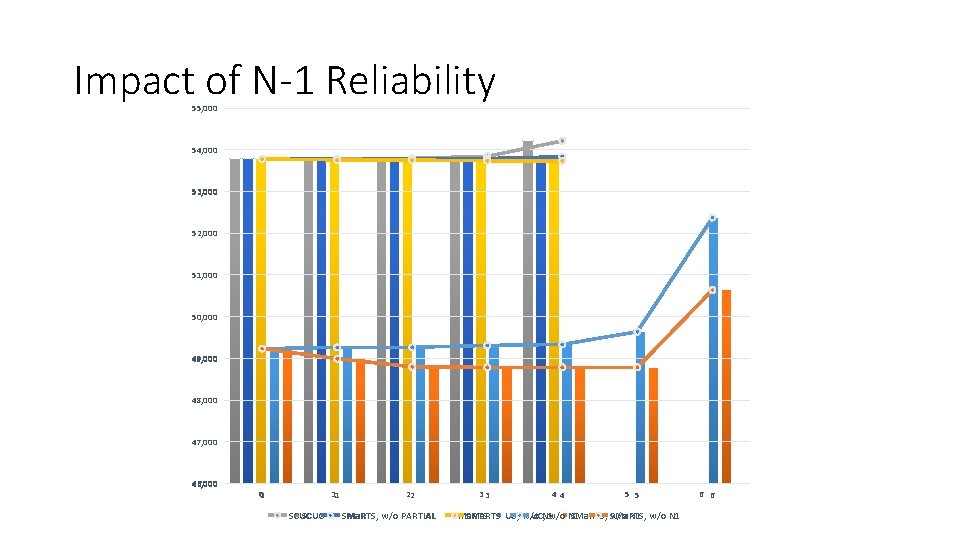
Results Business-as-Usual Model The SMa. RTS Model 0 1 2 3 4 5 Total Operating Cost ($) 53, 781. 71 53, 756. 47 53, 753. 67 53, 736. 75 Infeasible 6 infeasible Approved Line ID(s) --7 7, 18, 31, 38 - The SMa. RTS Model w/ no Partial Maintenance 0 1 2 3 4 5 Total Operating Cost ($) 53, 781. 71 53, 772. 01 53, 773. 44 53, 790. 29 53, 833. 21 Infeasible 6 infeasible Approved Line ID(s) --7 7, 38 7, 18, 31, 38 - 0 1 2 3 4 5 6 Total Operating Cost ($) 53, 781. 71 53, 783. 72 53, 795. 89 53, 842. 87 54, 211. 41 Infeasible Approved Line ID(s) ---38 38, 7, 18, 31 -

Results $54, 300 $54, 200 $54, 100 $54, 000 $53, 900 $53, 800 $53, 700 $53, 600 $53, 500 $53, 400 0 0 1 1 2 2 SCUCSMa. RTS, w/o PARTIAL 3 3 SMa. RTS 4 4

Impact of N-1 Reliability 55, 000 54, 000 53, 000 52, 000 51, 000 50, 000 49, 000 48, 000 47, 000 46, 000 00 11 SCUC 22 SMa. RTS, w/o PARTIAL 33 4 4 5 5 SMa. RTS, w/o N 1 SMa. RTS UC, w/o N 1 SMa. RTS, w/o N 1 6 6

Conclusion PART I - SDP Based Transmission Topology Control • AC Model with physical flow limits • Up to 9% cost reduction • Guaranteed to find a better topology PART II - The SMa. RTS Model • A new method to utilize Transmission Switching in Outage Coordination • Method to discard additional variable for N-1 • Up to 4% daily cost reduction • NYISO - daily operating cost is $15 Million.

Thank you. Gokturk Poyrazoglu gokturkp@buffalo. edu University at Buffalo, SUNY Department of Electrical Engineering