Optimization 1 General Problem 2 One Independent Variable

Optimization 1

General Problem 2

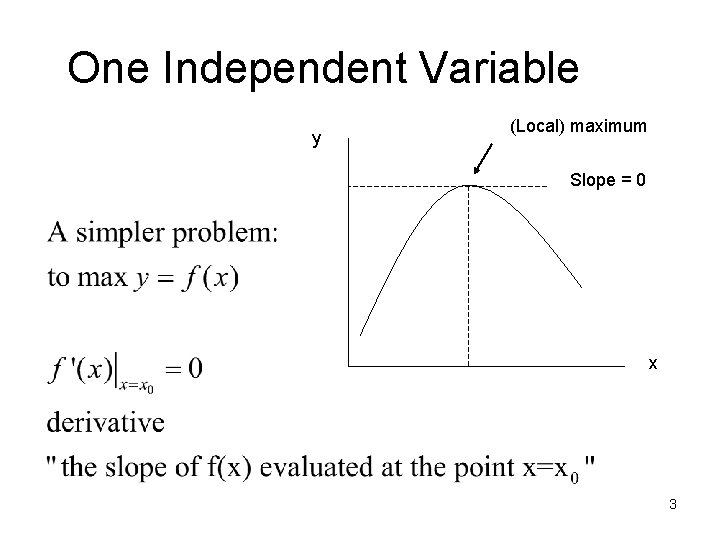
One Independent Variable y (Local) maximum Slope = 0 x 3

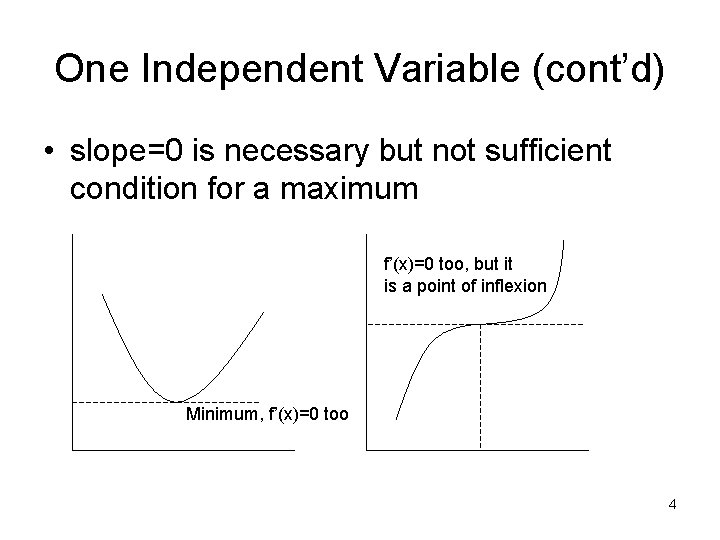
One Independent Variable (cont’d) • slope=0 is necessary but not sufficient condition for a maximum f’(x)=0 too, but it is a point of inflexion Minimum, f’(x)=0 too 4

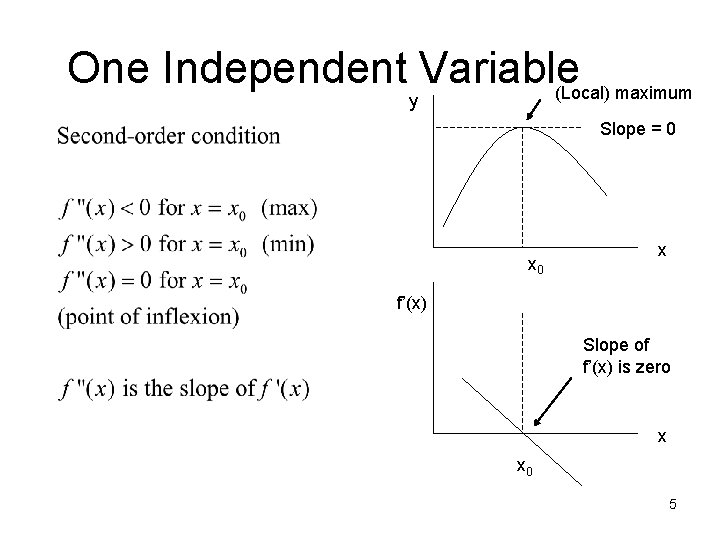
One Independent Variable (Local) maximum y Slope = 0 x f’(x) Slope of f’(x) is zero x x 0 5

One Independent Variable 6

Two Independent Variables y A z* x* x 7

Two Independent Variable 8

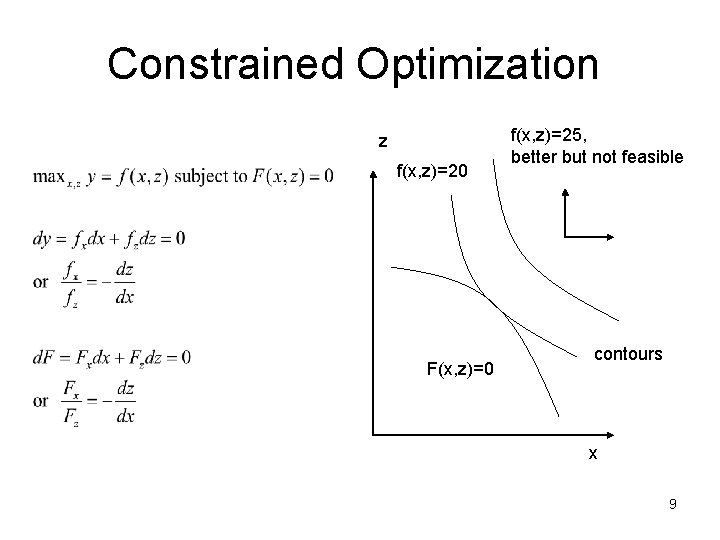
Constrained Optimization z f(x, z)=20 F(x, z)=0 f(x, z)=25, better but not feasible contours x 9

Constrained Optimization (cont’d) 10

Constrained Optimization (cont’d) 11

Lagrange’s method • Lagange’s method introduces a third variable called the Lagrangian multiplier (λ) that allows us to treat the problem as if an unconstrained one. 12

Lagrange’s method (cont’d) 13

Lagrange’s method 14

The Farmer’s Problem 15

The Farmer’s Problem (cont’d) 16

Envelope theorem 17

Envelope theorem (Cont’d) • The total derivative of the maximum value of y with respect to α is just equal to the partial derivative of y with respect to α, evaluated at the optimal choice of the xi’s. • This is called envelope theorem! 18

Envelope theorem (cont’d) 19

Envelope theorem (cont’d) 20