Optimal Placement of Wind Turbines Using Genetic Algorithms

Optimal Placement of Wind Turbines Using Genetic Algorithms Michael Case, North Georgia College Shannon Grady, Mentor

Outline l l l l Background Problem Genetic Algorithm Modeling of Wind Farm Results MATLAB Compiler Future Research

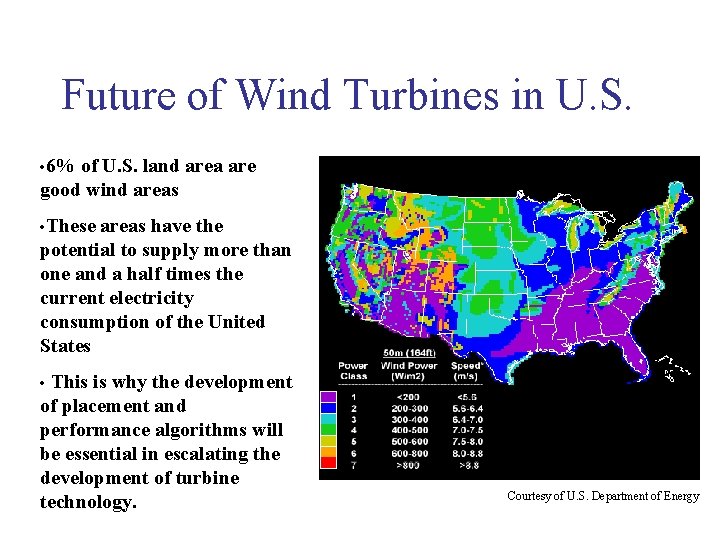
Future of Wind Turbines in U. S. • 6% of U. S. land area are good wind areas • These areas have the potential to supply more than one and a half times the current electricity consumption of the United States This is why the development of placement and performance algorithms will be essential in escalating the development of turbine technology. • Courtesy of U. S. Department of Energy

Wind Energy Research and Development • A very conventional wind farm located in Denmark. • The method used to the position the turbines seen here produces results similar to the genetic algorithm method employed here. http: //www. afm. dtu. dk/wind/turbines/gallery. htm

Offshore Turbine Development • Denmark is one of the leading nations in Wind Turbine technology, and is leading the way in offshore wind farm development. • D. O. E. plans to convert abandoned offshore oil rigs into wind farms off the Louisiana Coast are already in action. http: //www. afm. dtu. dk/wind/turbines/gallery. htm

Why Use Genetic Algorithms? l l Efficiency is affected by positioning in wind farms for multi-megawatt energy production Genetic Algorithms optimize the power output without dependence on gradients or local maxima

The Problem • To use genetic search algorithms to support the findings of scientists in the wind industry who have sought to find the optimal positioning for wind turbines based on cost and power output. Genetic Algorithms converge rapidly for the “NP-Complete” class of problems, as more parameters are introduced into a system genetic algorithms usually become more and more efficient then other search algorithms that have been used to solve nonlinear problems of this class, which makes it ideal for our research involving turbine placement.

Genetic Algorithm • Initially- Generate random population of n chromosomes (sqrt(200)*n, preferably) • Fitness- Evaluate the fitness f(x) of each chromosome x in the population • New population-Create a new population by repeating following steps until the new population is complete

Genetic Algorithms • Selection- Chromosomes from a population are selected according to their fitness (more fit individuals have greater chance) • See roulette wheel for example No. String Fitness % of Total 1 01101 169 14. 4 2 11000 576 49. 2 3 01000 64 5. 5 4 10011 361 30. 9 1170 100. 0 Total

Genetic Algorithms l Crossover- With a crossover probability cross over the parents to form new offspring (children). If no crossover was performed, offspring is the exact copy of parents. We used a crossover rate of. 75. Chromosome 1 11011 | 00100110110 Chromosome 2 11011 | 11000011110 Offspring 1 11011 | 11000011110 Offspring 2 11011 | 00100110110

Genetic Algorithms • Mutation- With a mutation probability mutate new offspring at each locus (position in chromosome). It is important to keep the mutation rate low (. 001) to keep the search from becoming random. Original offspring 1 1101111000011110 Original offspring 2 1101100100110110 Mutated offspring 1 1100111000011110 Mutated offspring 2 110110110

Genetic Algorithm • Replacement- Use new generated population for a further run of the algorithm • Evaluate-If the end condition is satisfied, stop, and return the best solution in current population • Loop- Continue evaluating Fitness until the search terminates at 100%efficiency or the number of generations you assign is reached

Modeling a Wind Farm Velocity Downstream for a single turbine: Thrust Coefficient: u = wind speed downstream from the turbine u 0 = initial wind speed α = entertainment constant α =axial induction r 1 =down stream rotor radius x = distance downstream the turbine The turbine thrust coefficient and the downstream rotor radius are linked to the axial induction factor α, and the rotor radius, Rr , by the Betz relations.

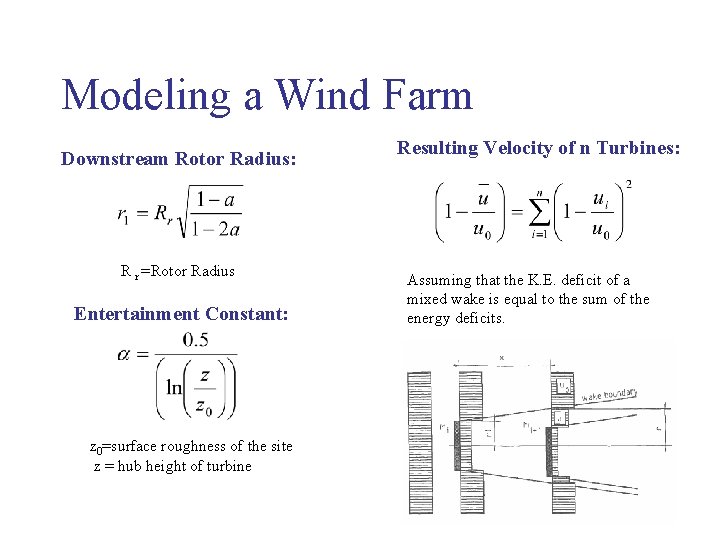
Modeling a Wind Farm Downstream Rotor Radius: R r =Rotor Radius Entertainment Constant: z 0=surface roughness of the site z = hub height of turbine Resulting Velocity of n Turbines: Assuming that the K. E. deficit of a mixed wake is equal to the sum of the energy deficits.

Cost and Fitness Functions Cost Function: Fitness Function: Ptot=total Power Nt =Number of Turbines Costtot=yearly cost ω1, 2=act as weights for the fitness function.

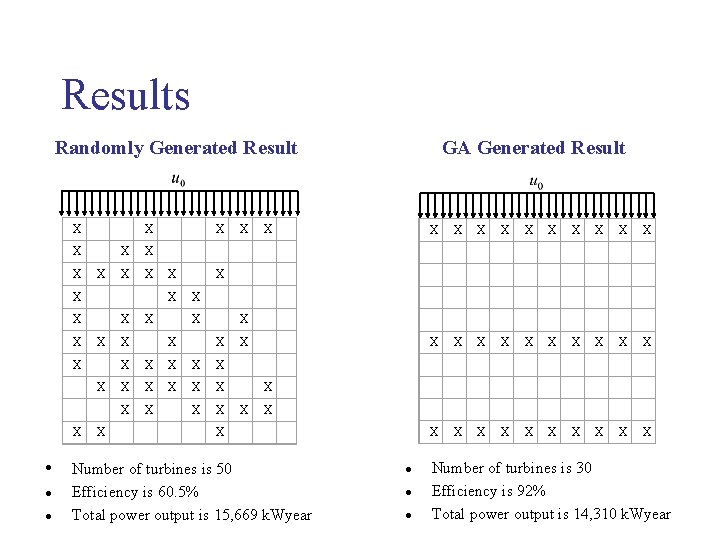
Results GA Generated Result Randomly Generated Result • l l X X X X X X X X X X X X X X X X X X X X X X X X X X X X Number of turbines is 50 Efficiency is 60. 5% Total power output is 15, 669 k. Wyear l l l Number of turbines is 30 Efficiency is 92% Total power output is 14, 310 k. Wyear

The MATLAB Compiler • The MATLAB Compiler is a very powerful tool that can be used to create code from M-Files to C, C++, or Fortran 90/95 for a various number of platforms, and will allow for thousands of generations to be run on SP 3 here at CSIT. http: //www. csit. fsu. edu/supercomputer/fsu-sp. html

Future Research l l l Parametric study of objective function and cost functions for various turbine models on land sea Stochastic wind modeling and evaluation of equilibrium techniques Incorporation of helical wake model Introduction of simulated annealing into the optimization process Evaluation and development of cost/maintenance models