Optimal output selection for batch processes Hkon DahlOlsen

Optimal output selection for batch processes Håkon Dahl-Olsen, Sridharakumar Narasimhan and Sigurd Skogestad

Outline • Batch optimization • Implementation schemes • Variable selection method • Reactor case study • Summary

Batch optimization • Minimum time to given specification • Maximum product in fixed time

Dynamic optimization

Implementation • Online optimization: measurements used to update model • Self-optimizing control: good outputs give near optimal performance

Variable selection • Unconstrained degrees of freedom • Based on Pontryagin’s minimum principle • Look for variables which give small deviation from optimality when controlled at fixed reference, even under disturbances

Maximum gain rule • Loss is defined in terms of value of the Hamiltonian • The loss is time-varying

Maximum gain rule Need to relate variations in inputs to variations in outputs

Maximum gain rule for dynamic optimization • Assume the model is scaled such that δymax≈1 Select y’s to minimize the following expression along the nominal trajectory

How to obtain G • How does variations in inputs map to the states? • Neighboring optimal control gives δu(t)=K(t)δx(t) • We estimate G by

Example • Bioreactor Maximize production of product P in a fed-batch bioreactor with fixed final time of 150 hours • Reaction is driven by the presence of a substrate S, which is consumed in the biomass generation • The biomass concentration is constrained Srinivasan, B. , D. Bonvin, et al. (2002). "Dynamic optimization of batch processes II. Role of measurements in handling uncertainty. " Comp. chem. eng. 27: 27 -44.

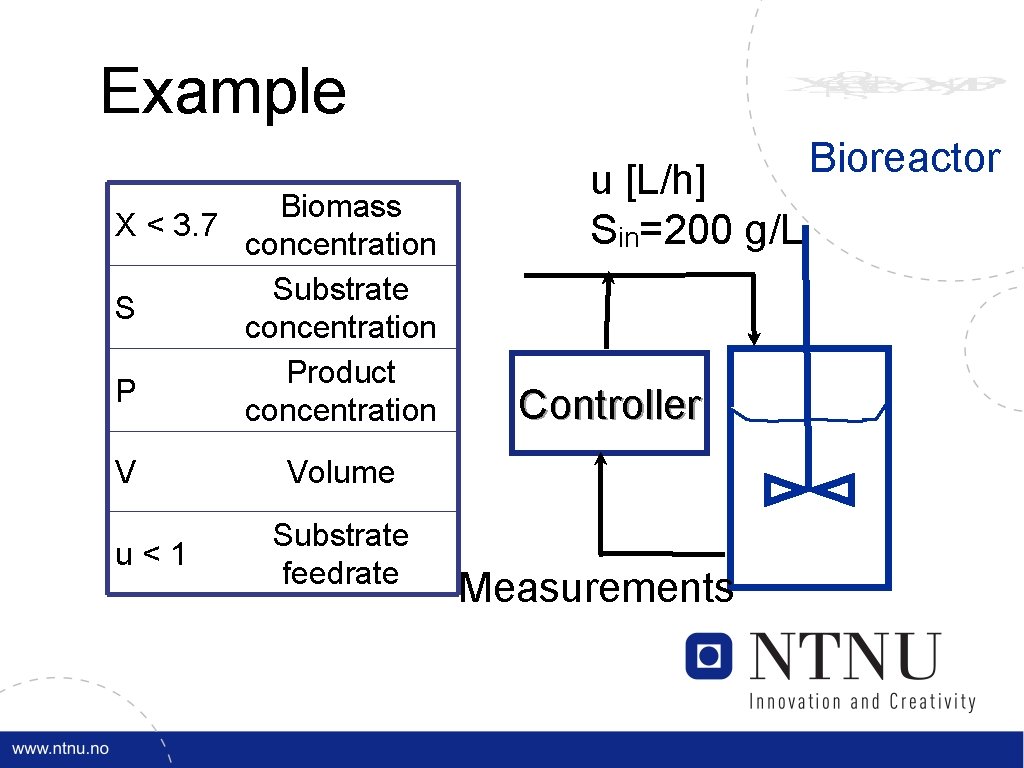
Example Biomass X < 3. 7 concentration Substrate S concentration Product P concentration V u<1 u [L/h] Sin=200 g/L Controller Volume Substrate feedrate Measurements Bioreactor

Example Bioreactor Biomass X < 3. 7 concentration Substrate S concentration Product P concentration V u<1 Volume Substrate feedrate

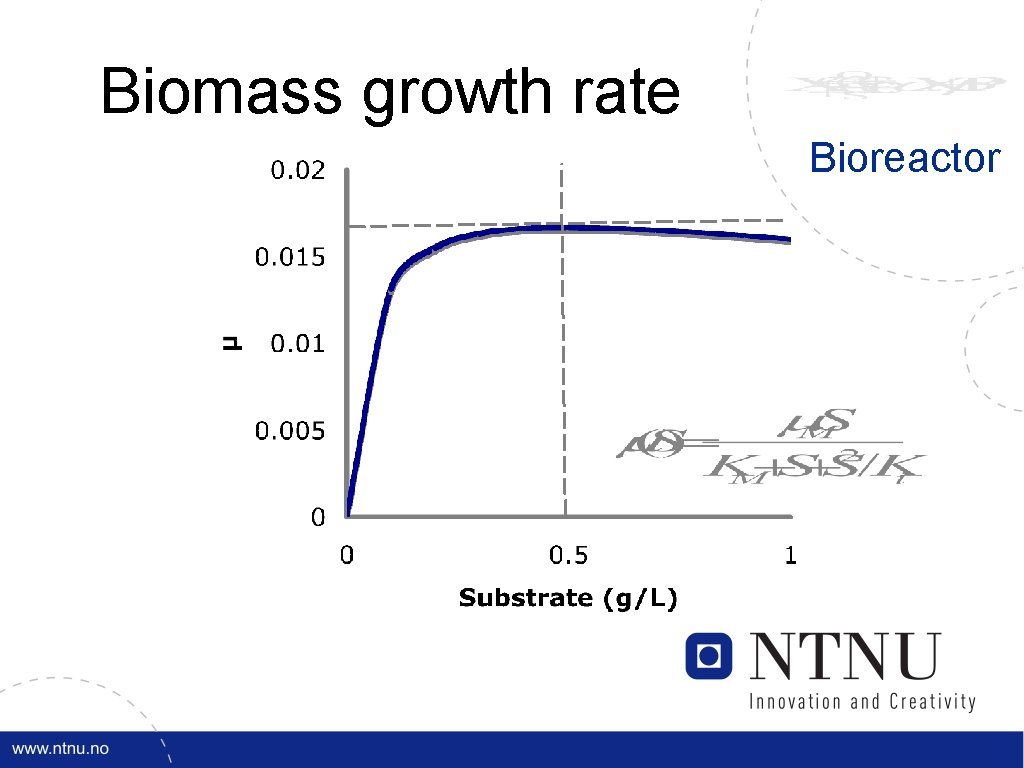
Biomass growth rate Bioreactor

Consider gain magnitude Bioreactor • Transformation of input: ξ=√u • H is constant • Minimizing of 1/K corresponds to ξξ 2 maximizing K 2

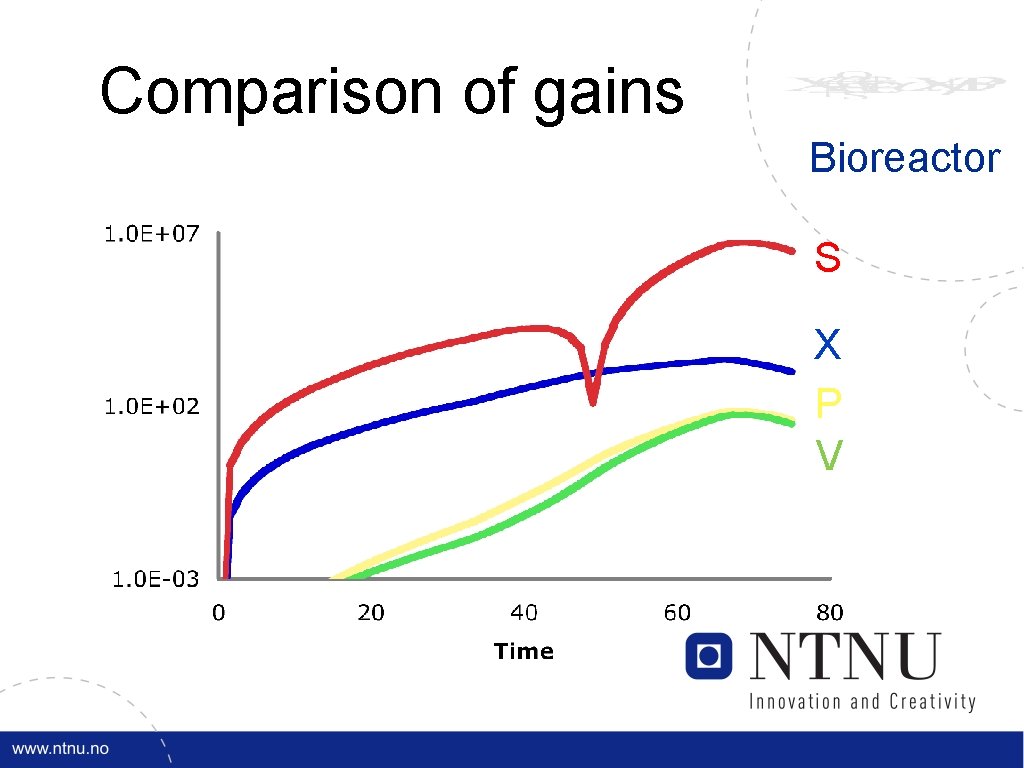
Comparison of gains Bioreactor S X P V

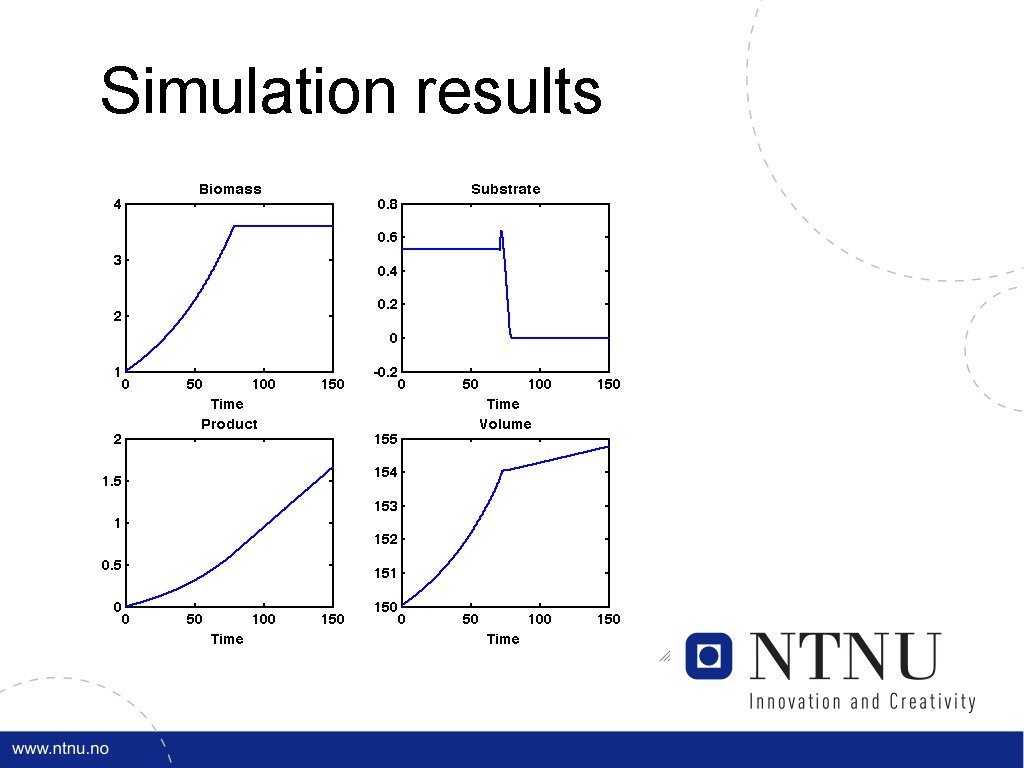
Simulation results

Summary • Maximum gain rule extended to dynamics • Variational gain from neighboring optimal control theory • Method works well for a small case study